2019年湖北省孝感市中考数学真题及答案.doc-资料库

第1页 / 共30页

第2页 / 共30页

第3页 / 共30页

第4页 / 共30页

第5页 / 共30页

第6页 / 共30页

第7页 / 共30页

第8页 / 共30页

2019 年湖北省孝感市中考数学真题及答案一、精心选一选，相信自己的判断！（本大题共 10 小题，每小题 3 分，共 30 分） 1．（3 分）计算﹣19+20 等于（） A．﹣39 B．﹣1 C．1 D．39 2．（3 分）如图，直线 l1∥l2，直线 l3 与 l1，l2 分别交于点 A，C，BC⊥l3 交 l1 于点 B，若∠1＝70°，则∠2 的度数为（） A．10° B．20° C．30° D．40° 3．（3 分）下列立体图形中，左视图是圆的是（） A． C． B． D． 4．（3 分）下列说法错误的是（） A．在一定条件下，可能发生也可能不发生的事件称为随机事件 B．一组数据中出现次数最多的数据称为这组数据的众数 C．方差可以刻画数据的波动程度，方差越大，波动越小；方差越小，波动越大 D．全面调查和抽样调查是收集数据的两种方式 5．（3 分）下列计算正确的是（） A．x7÷x5＝x2 B．（xy2）2＝xy4

C．x2•x5＝x10 D．（ + ）（ ﹣ ）＝b﹣a 6．（3 分）公元前 3 世纪，古希腊科学家阿基米德发现了杠杆平衡，后来人们把它归纳为“杠杆原理”，即：阻力×阻力臂＝动力×动力臂．小伟欲用撬棍撬动一块石头，已知阻力和阻力臂分别是 1200N和 0.5m，则动力 F（单位：N）关于动力臂 l（单位：m）的函数解析式正确的是（） A．F＝ B．F＝ C．F＝ D．F＝ 7．（3 分）已知二元一次方程组，则的值是（） A．﹣5 B．5 C．﹣6 D．6 8．（3 分）如图，在平面直角坐标系中，将点 P（2，3）绕原点 O顺时针旋转 90°得到点 P'，则 P'的坐标为（） A．（3，2） B．（3，﹣1） C．（2，﹣3） D．（3，﹣2） 9．（3 分）一个装有进水管和出水管的空容器，从某时刻开始 4min内只进水不出水，容器内存水 8L；在随后的 8min内既进水又出水，容器内存水 12L；接着关闭进水管直到容器内的水放完．若每分钟进水量和出水量是两个常数，容器内的水量 y（单位：L）与时间 x（单位：min）之间的函数关系的图象大致的是（） A． C． B． D． 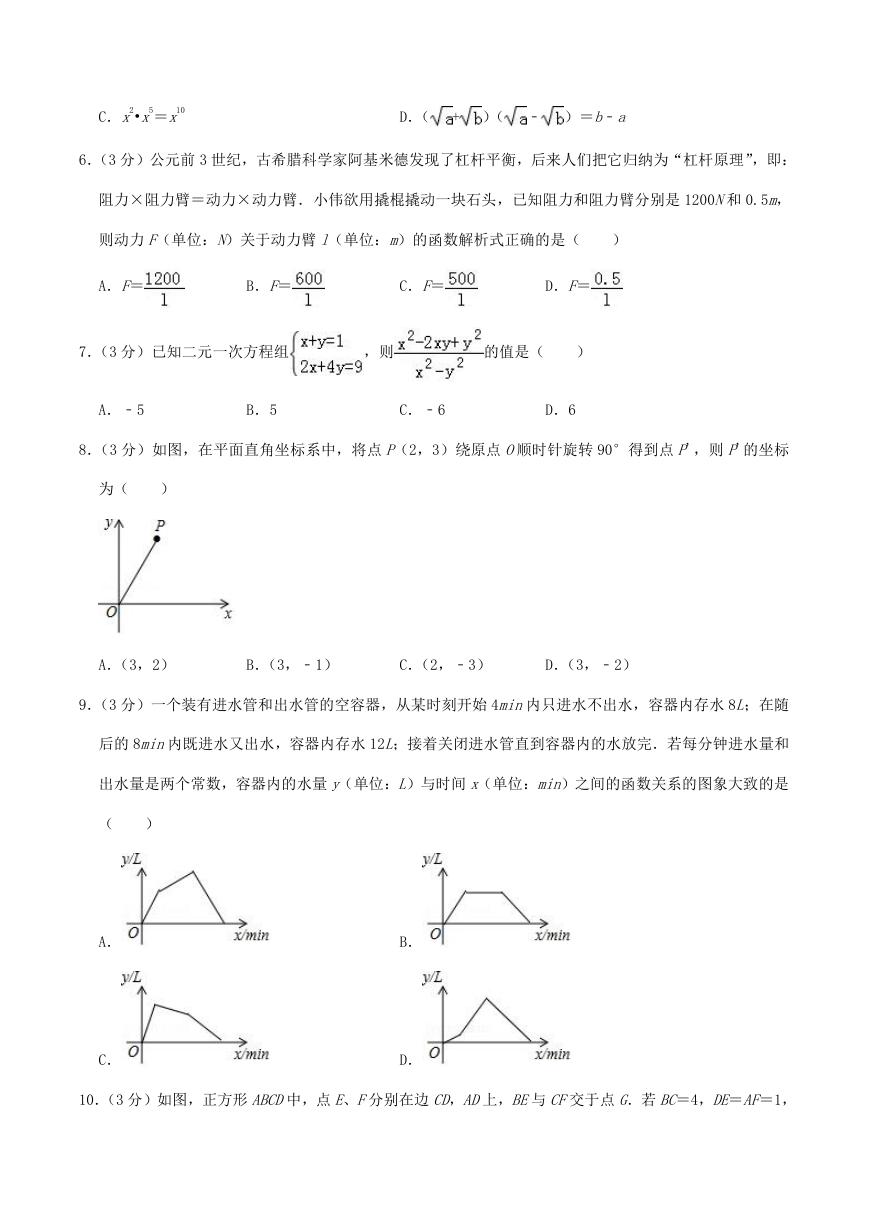10．（3 分）如图，正方形 ABCD中，点 E、F分别在边 CD，AD上，BE与 CF交于点 G．若 BC＝4，DE＝AF＝1，

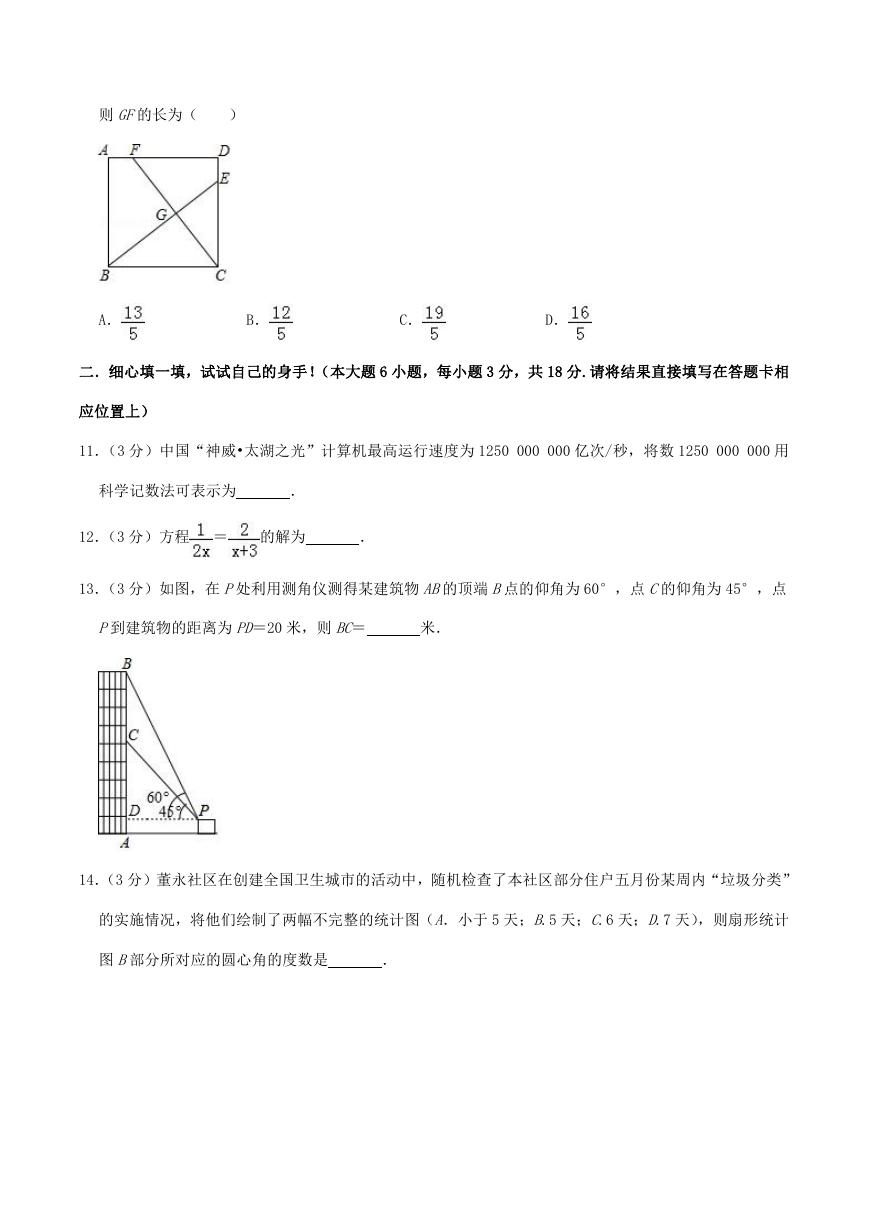
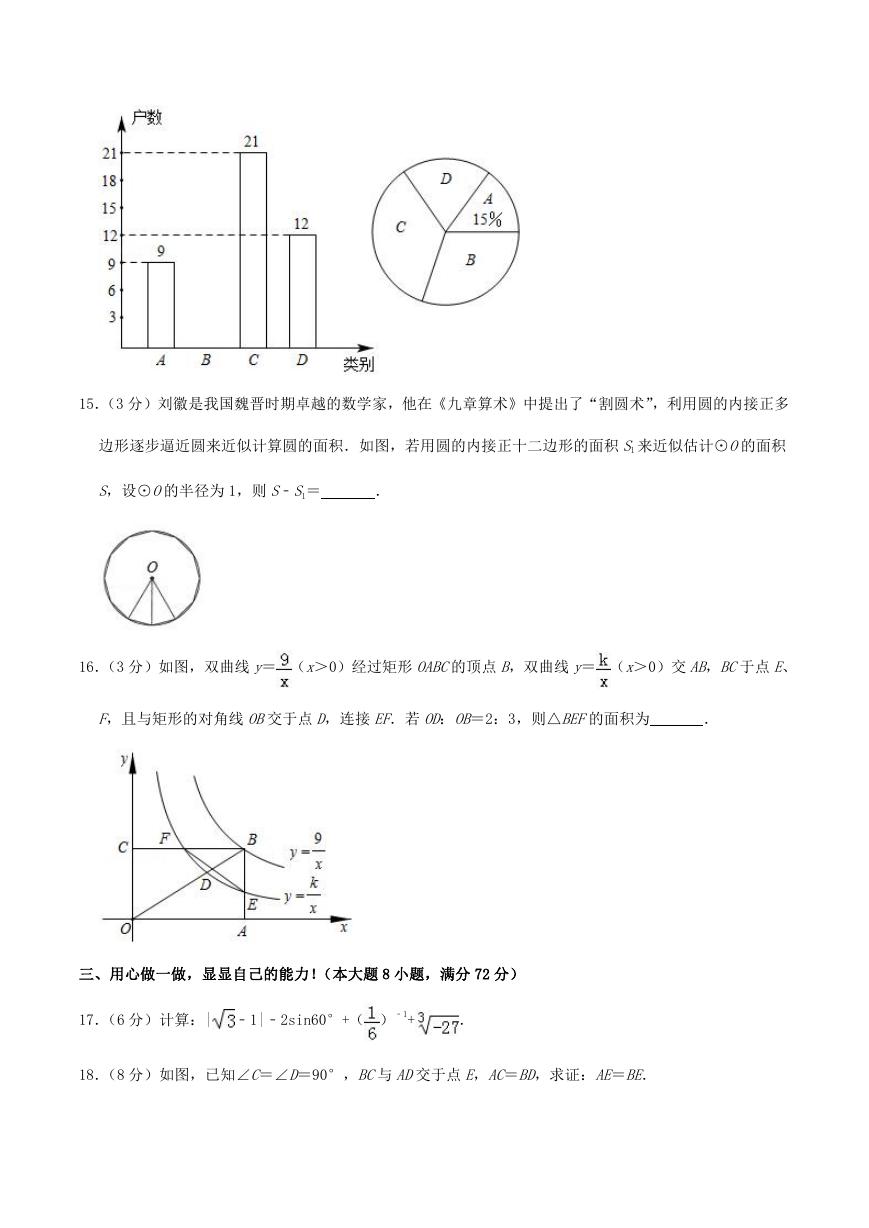
则 GF的长为（） A． B． C． D．二．细心填一填，试试自己的身手！（本大题 6 小题，每小题 3 分，共 18 分.请将结果直接填写在答题卡相应位置上） 11．（3 分）中国“神威•太湖之光”计算机最高运行速度为 1250 000 000 亿次/秒，将数 1250 000 000 用科学记数法可表示为． 12．（3 分）方程＝的解为． 13．（3 分）如图，在 P处利用测角仪测得某建筑物 AB的顶端 B点的仰角为 60°，点 C的仰角为 45°，点 P到建筑物的距离为 PD＝20 米，则 BC＝米． 14．（3 分）董永社区在创建全国卫生城市的活动中，随机检查了本社区部分住户五月份某周内“垃圾分类” 的实施情况，将他们绘制了两幅不完整的统计图（A．小于 5 天；B.5 天；C.6 天；D.7 天），则扇形统计图 B部分所对应的圆心角的度数是．

15．（3 分）刘徽是我国魏晋时期卓越的数学家，他在《九章算术》中提出了“割圆术”，利用圆的内接正多边形逐步逼近圆来近似计算圆的面积．如图，若用圆的内接正十二边形的面积 S1 来近似估计⊙O的面积 S，设⊙O的半径为 1，则 S﹣S1＝． 16．（3 分）如图，双曲线 y＝（x＞0）经过矩形 OABC的顶点 B，双曲线 y＝（x＞0）交 AB，BC于点 E、 F，且与矩形的对角线 OB交于点 D，连接 EF．若 OD：OB＝2：3，则△BEF的面积为．三、用心做一做，显显自己的能力！（本大题 8 小题，满分 72 分） 17．（6 分）计算：| ﹣1|﹣2sin60°+（）﹣1+ ． 18．（8 分）如图，已知∠C＝∠D＝90°，BC与 AD交于点 E，AC＝BD，求证：AE＝BE．

19．（7 分）一个不透明的袋子中装有四个小球，上面分别标有数字﹣2，﹣1，0，1，它们除了数字不同外，其它完全相同．（1）随机从袋子中摸出一个小球，摸出的球上面标的数字为正数的概率是．（2）小聪先从袋子中随机摸出一个小球，记下数字作为平面直角坐标系内点 M的横坐标；然后放回搅匀，接着小明从袋子中随机摸出一个小球，记下数字作为点 M的纵坐标．如图，已知四边形 ABCD的四个顶点的坐标分别为 A（﹣2，0），B（0，﹣2），C（1，0），D（0，1），请用画树状图或列表法，求点 M落在四边形 ABCD所围成的部分内（含边界）的概率． 20．（8 分）如图，Rt△ABC中，∠ACB＝90°，一同学利用直尺和圆规完成如下操作： ①以点 C为圆心，以 CB为半径画弧，交 AB于点 G；分别以点 G、B为圆心，以大于 GB的长为半径画弧，两弧交点 K，作射线 CK； ②以点 B为圆心，以适当的长为半径画弧，交 BC于点 M，交 AB的延长线于点 N；分别以点 M、N为圆心，以大于 MN的长为半径画弧，两弧交于点 P，作直线 BP交 AC的延长线于点 D，交射线 CK于点 E．

请你观察图形，根据操作结果解答下列问题；（1）线段 CD与 CE的大小关系是；（2）过点 D作 DF⊥AB交 AB的延长线于点 F，若 AC＝12，BC＝5，求 tan∠DBF的值． 21．（10 分）已知关于 x的一元二次方程 x2﹣2（a﹣1）x+a2﹣a﹣2＝0 有两个不相等的实数根 x1，x2．（1）若 a为正整数，求 a的值；（2）若 x1，x2 满足 x1 2+x2 2﹣x1x2＝16，求 a的值． 22．（10 分）为加快“智慧校园”建设，某市准备为试点学校采购一批 A、B两种型号的一体机．经过市场调查发现，今年每套 B型一体机的价格比每套 A型一体机的价格多 0.6 万元，且用 960 万元恰好能购买 500 套 A型一体机和 200 套 B型一体机．（1）求今年每套 A型、B型一体机的价格各是多少万元？（2）该市明年计划采购 A型、B型一体机共 1100 套，考虑物价因素，预计明年每套 A型一体机的价格比今年上涨 25%，每套 B型一体机的价格不变，若购买 B型一体机的总费用不低于购买 A型一体机的总费用，那么该市明年至少需要投入多少万元才能完成采购计划？ 23．（10 分）如图，点 I是△ABC的内心，BI的延长线与△ABC的外接圆⊙O交于点 D，与 AC交于点 E，延长 CD、BA相交于点 F，∠ADF的平分线交 AF于点 G．（1）求证：DG∥CA；（2）求证：AD＝ID；（3）若 DE＝4，BE＝5，求 BI的长．

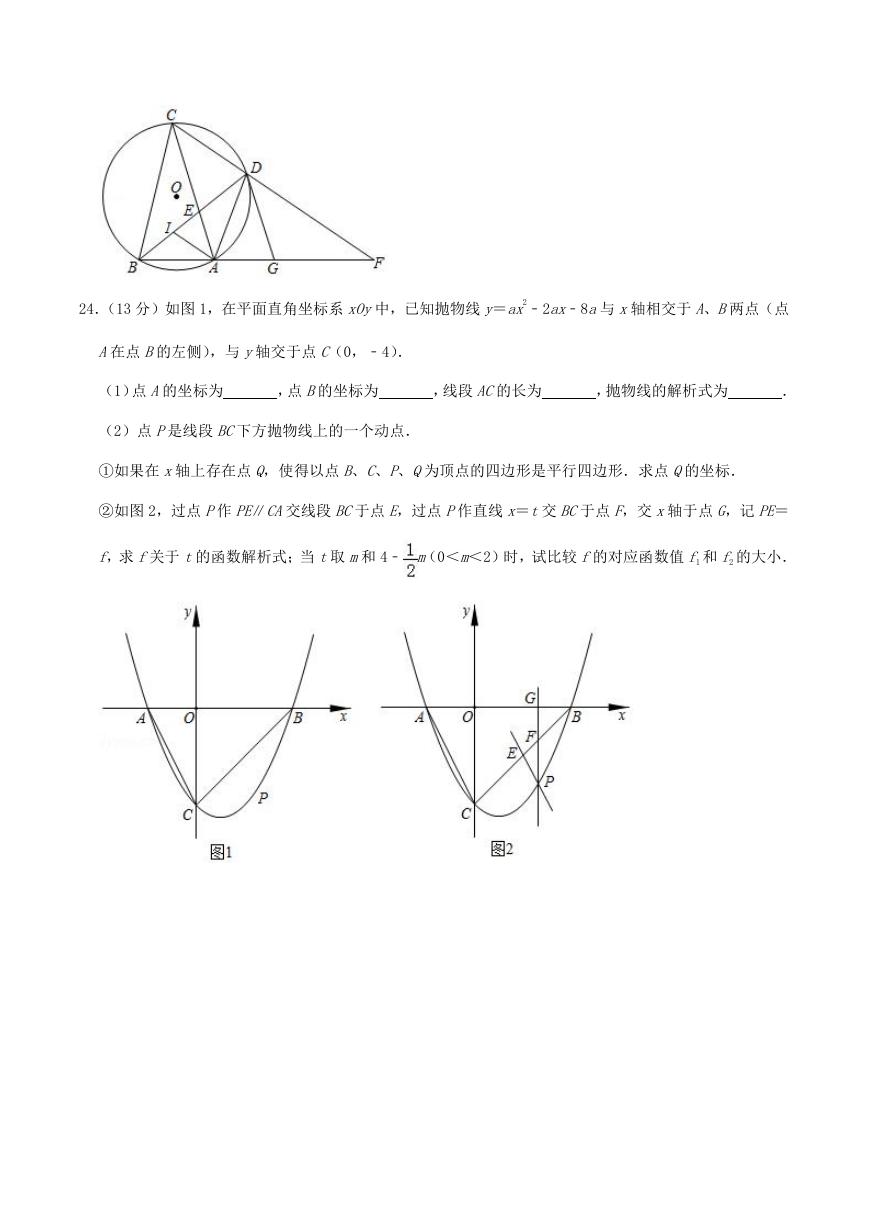
24．（13 分）如图 1，在平面直角坐标系 xOy中，已知抛物线 y＝ax2﹣2ax﹣8a与 x轴相交于 A、B两点（点 A在点 B的左侧），与 y轴交于点 C（0，﹣4）．（1）点 A的坐标为，点 B的坐标为，线段 AC的长为，抛物线的解析式为．（2）点 P是线段 BC下方抛物线上的一个动点． ①如果在 x轴上存在点 Q，使得以点 B、C、P、Q为顶点的四边形是平行四边形．求点 Q的坐标． ②如图 2，过点 P作 PE∥CA交线段 BC于点 E，过点 P作直线 x＝t交 BC于点 F，交 x轴于点 G，记 PE＝ f，求 f关于 t的函数解析式；当 t取 m和 4﹣ m（0＜m＜2）时，试比较 f的对应函数值 f1 和 f2 的大小．

2019 年湖北省孝感市中考数学试卷一、精心选一选，相信自己的判断！（本大题共 10 小题，每小题 3 分，共 30 分）参考答案与试题解析 1．（3 分）计算﹣19+20 等于（） A．﹣39 B．﹣1 C．1 D．39 【分析】直接利用有理数的加减运算法则计算得出答案．【解答】解：﹣19+20＝1．故选：C．【点评】此题主要考查了有理数的加减运算，正确掌握运算法则是解题关键． 2．（3 分）如图，直线 l1∥l2，直线 l3 与 l1，l2 分别交于点 A，C，BC⊥l3 交 l1 于点 B，若∠1＝70°，则∠2 的度数为（） A．10° B．20° C．30° D．40° 【分析】根据平行线的性质和垂直的定义解答即可．【解答】解：∵l1∥l2， ∴∠1＝∠CAB＝70°， ∵BC⊥l3 交 l1 于点 B， ∴∠ACB＝90°， ∴∠2＝180°﹣90°﹣70°＝20°，故选：B．【点评】此题考查平行线的性质，关键是根据平行线的性质解答． 3．（3 分）下列立体图形中，左视图是圆的是（）

资料库

2019年湖北省孝感市中考数学真题及答案.doc

相关推荐

中考

热门标签

最新资料