第1页 / 共16页
第2页 / 共16页
第3页 / 共16页
第4页 / 共16页
第5页 / 共16页
第6页 / 共16页
第7页 / 共16页
第8页 / 共16页
effective SNR mapping for modeling frame error rates in multiple....pdf
3GPP2-C30-20030429-010
WG3
TITLE: Effective-SNR Mapping for Modeling Frame Error Rates in Multiple-state
Channels
SOURCE:
shawn.tsai@ericsson.com
anthony.soong@ericsson.com
S. Shawn Tsai
Anthony C. K. Soong
ABSTRACT:
This contribution provides Ericsson’s view on effective-SNR mapping (ESM) for frame
error rate (FER) characterization of multiple-state channels. The requirements for a good
ESM are given from a theoretical point of view. Several ESM functions are studied and their
accuracies are verified through simulations. It is found that the mapping based on the mutual
information translates turbo-coded R-SCH FER to AWGN with less-than-0.1dB errors for
all Strawman channel models. For convolutional codes, the exponential ESM is developed
and its effectiveness is verified through simulations. The exponential ESM can reach an
accuracy of
RECOMMENDATION:
FYI
dB under a wide range of SNR variations.
2.0–
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
Ericsson Wireless Communication Incorporated grants a free, irrevocable license to
3GPP2 and its Organizational Partners to incorporate text or other copyright-
able material contained in the contribution and any modifications thereof in the
creation of 3GPP2 publications; to copyright and sell in Organizational Partner's
name any Organizational Partner's standards publication even though it may
include all or portions of this contribution; and at the Organizational Partner's
sole discretion to permit others to reproduce in whole or in part such contribu-
tion or the resulting Organizational Partner's standards publication. Ericsson
Wireless Communication Incorporated is also willing to grant licenses under
such contributor copyrights to third parties on reasonable, non-discriminatory
terms and conditions for purpose of practicing an Organizational Partner’s
standard which incorporates this contribution.
This document has been prepared by Ericsson Wireless Communication Incor-
porated to assist the development of specifications by 3GPP2. It is proposed to
the Committee as a basis for discussion and is not to be construed as a binding
proposal on Ericsson Wireless Communication Incorporated. Ericsson Wireless
Communication Incorporated specifically reserves the right to amend or modify
the material contained herein and to any intellectual property of Ericsson Wire-
less Communication Incorporated other than provided in the copyright state-
ment above.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
3GPP2-C30-20030429-010
Introduction
1
Currently, all reverse link enhancement proposals are evaluated based on Strawman with
five different channels models. Different Doppler speeds (3km/hr to 120km/hr) result in
differences in FER even with short-term average of SNR (frame SNR). In addition, cur-
rent proposals all include hybrid ARQ. With multiple retransmissions in channels with
high Doppler, each frame is under influence from multiple channel states. Since there ex-
ist many possible combinations of SNR in system simulations, exhaustive link results
would be a formidable task. How to map SNR of multiple-state channels to model FER
performance becomes a key to reliable system results. This contribution provides an ini-
tial step to solve this problem.
2 Equivalent-SNR Mapping: A Theoretical Point of View
With the assumption of ideal channel state information, the “capacity”1 of a multiple-
state channel can be computed as2
(
)
I
eff
=
=
( )
d
I
( )
(
I
f
i
SNR
)
p
i
i
f
SNR
( )g
where
symbol SNR g
The goal of effective-SNR mapping (ESM) is to find
f
(
=
I
I
1
e
ff
is the probability density function (pdf) for continuous-valued channel
and
.
ip is the probability mass function (pmf) for discrete-valued SNR
i
( )
(
I
)
( )
d
SNR
)
i
p
i
=
I
1
i
Notice that the channel capacity is a well-defined term in information theory. In this sec-
tion, a loose term “information measure” is used to name the function
that character-
izes the channel capacity. Some commonly known information measures are listed as fol-
lows:
1. Mutual information MII
( )gI
:
For BPSK in an AWGN channel, the mutual information is defined as
(
)
XYP
,
) (
(
XYPXP
where X is the binary input and Y is the channel output.
( )
=g
log 2
E
XY
MI
I
X
)
,
2. AWGN channel capacity
I
ACC
( )g
I
ACC
:
( )
=g
(
1
)g+
log
2
1
2
1 Note that function ( )gI
2 The average of “capacity” by the probability distribution is commonly seen in theoretical analysis. Usu-
ally the form of the capacity curves does not change dramatically. For Rayleigh fading and energy con-
strained signaling, the difference from the static AWGN is 2.5 dB asymptotically [2]. For channels with
smaller dynamic SNR range, the difference from the AWGN channel capacity is not as large.
may not be the well-defined channel capacity in the information theory.
g
g
g
g
g
g
ł
Ł
g
g
g
g
g
-
-
g
g
Notice that the channel input is not constrained on a given modulation format.
3. Cutoff rate
0RI
( )g
:
For BPSK, the cutoff rate is expressed as
log
( )
-=g
1
I R
0
4. Linear SNR value
( )g
:
linI
(
1
2
-+
e
)2/
It is common to use SNR directly as an information measure, i.e.,
5. SNR value in dB
( )g
:
logI
( )
g=g
linI
( )
=g
( )g
log
logI
1
2
3
4
5
6
7
8
9
10
11
12
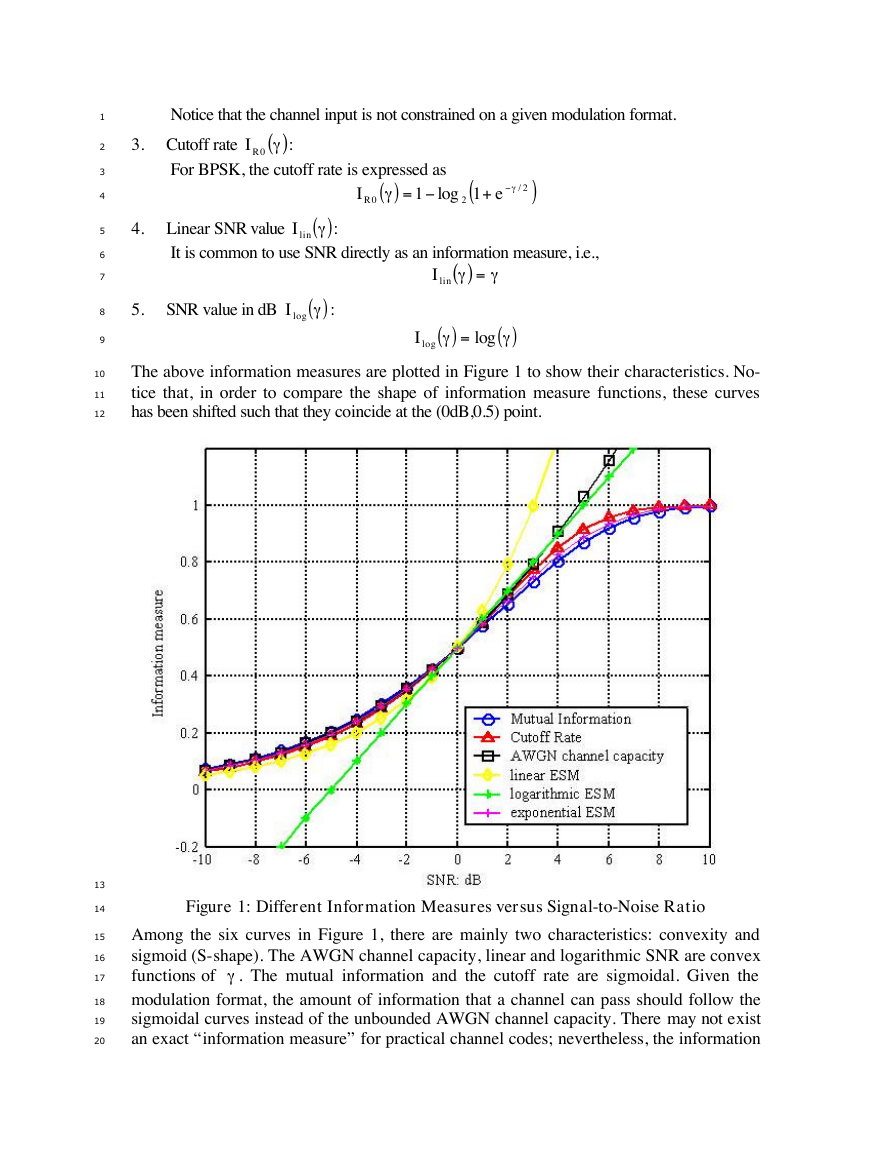
The above information measures are plotted in Figure 1 to show their characteristics. No-
tice that, in order to compare the shape of information measure functions, these curves
has been shifted such that they coincide at the (0dB,0.5) point.
13
14
15
16
17
18
19
20
Figure 1: Different Information Measures versus Signal-to-Noise Ratio
Among the six curves in Figure 1, there are mainly two characteristics: convexity and
sigmoid (S-shape). The AWGN channel capacity, linear and logarithmic SNR are convex
functions of g
. The mutual information and the cutoff rate are sigmoidal. Given the
modulation format, the amount of information that a channel can pass should follow the
sigmoidal curves instead of the unbounded AWGN channel capacity. There may not exist
an exact “information measure” for practical channel codes; nevertheless, the information
g
measure should be bounded by the modulation format and the given bandwidth. It is pre-
dictable that, as the SNR gets higher, a convex function will overestimate the information
that can be delivered. Particularly, logarithmic ESM also underestimates the information
at low SNR. It is expected that practical channel codes with a given modulation format
will be better modeled by sigmoidal curves. Especially, for channel code with perform-
ance close to channel capacity under a fixed modulation format, the mutual information
would better describe the information delivered by the given channel symbol SNR.
Therefore, the key to effective-SNR mapping should lie in the sigmoidal property of the
information measure.
In Figure 1, in addition to the mutual information and the cutoff rate, an exponential in-
formation measure
is defined as
( )g
I
EXP
( )
-=g
1
(
exp
)g
I
EXP
The exponential information function leads to the exponential ESM
)
=
=
(
)
(
)
(
N
N
N
p
i
p
i
exp
I
EXP
i
p
i
I
EPX
eff
-=
1
i
=
1
i
=
i
1
=
i
1
-=
ln
e
ff
(
p
i
exp
)
i
N
=
1
i
(
exp
)
eff
The reason of including this function will be given in Section 4. Note that, with a proper
offset, the exponential ESM is similar to the sigmoidal mutual information curve in shape.
Several comments must be made before we proceed. First, since practical codes do not
exactly follow the information theoretic formulas, higher order errors can be expected.
The goal of the ESM should be kept as an effort to model the FER performance within
the range of interest. Second, since FER also depends on the correlation between bit er-
rors, extra modeling errors can be expected when compared with BER modeling. Third,
for any ESM applied to system level simulations with a granularity of PCG, not symbol,
linear ESM is applied first and hence extra errors will be introduced. Fourth, an ideal
ESM function should not be sensitive to different Doppler spreads. Otherwise, extensive,
if not exhaustive, simulations would still be needed to find proper parameter for different
cases.
3 Comparison of Multiple ESM Functions for IS-2000 R-SCH with Turbo Codes
For the case of mutual information ESM, a simple closed form expression is not available.
The following approximation is used (which is given in [1] and repeated here for easy
reference):
( )
g
=
I MI
22J
(
)g
where
and
( )
xJ
xa
1
1
3
+
exp
2
xb
(
1
xa
2
+
xc
,
1
+
xb
2
3
for
+
2
<<
x
+
0
dxc
2
2
.1
)
,
6363
for
.1
6363
¥<
x
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
-
ł
Ł
g
-
g
g
-
g
-
-
g
g
£
-
»
1
2
3
4
5
6
7
8
9
10
c
1
)
)
1
The coefficient values are given in Table 1 [1].
ya
a
ln
y
J
4
3
1
+
yb
3
(
(
yb
4
+
2
(
)
3646
y
1
for
y
,
yc
,
4
0
for
+
<<
y
.0
3646
.0
Table 1: Coefficient Values for BPSK Mutual Information Approximation
a1
-0.0421061
a2
0.00181491
a3
1.09542
a4
-0.706692
b1
0.209252
b2
-0.142675
b3
0.214217
b4
-0.386013
c1
-0.00640081
c2
-0.0822054
c3
2.33727
c4
1.75017
d2
0.0549608
Using the above approximations, we get the mutual information ESM as follows:
(
g
)
I
MI
=
1
N
1
N
and the effective SNR can be computed [1] by
N
eff
g
eff
I
1
MI
1
N
=
i
1
(
g
i
)
I
MI
(
22
)
g
i
J
N
=
i
1
N
=
i
1
(
g
22
i
J
(
g
22
)
i
)
2
1
J
1
N
N
=
i
1
J
For other ESM functions, their inverse is straightforward. The simulation assumptions are
summarized in Table 2.
8
Table 2: Summary of Simulation Assumptions
Frame length
Inner PC loop step size
PC command error
PC delay
Stopping criteria
Power estimation for power control
Channel estimation
Number of receive antennas
Turbo decoder type
Max number of iterations in the decoder
Outer-loop target FER
Outer-loop power control step size
20msec
1 dB
4%
2
50000 frames
Pilot channel energy of each PCG
Perfect
2
SubMAP (Max*)
8
5%
0.5dB up, 0.5/(1/target_FER-1)dB down
£
£
-
»
-
»
œ
ß
ø
Œ
º
Ø
ł
Ł
»
ł
Ł
»
-
-
The multipath interference (as in Model B and C) is approximated by a zero mean white
Gaussian noise process with variance equal to the total power on all other paths divided
by the processing gain. The inner-loop power control is based the estimate pilot energy of
each PCG, which is the total square of received pilot symbols divided by the number of
pilot symbols in one PCG. The initial value of the inner-loop target is set at the noise
level and is adjusted by the outer-loop power control. Except the ideal combining
coefficients for the RAKE receiver, all assumptions follow the current evaluation
methodology.
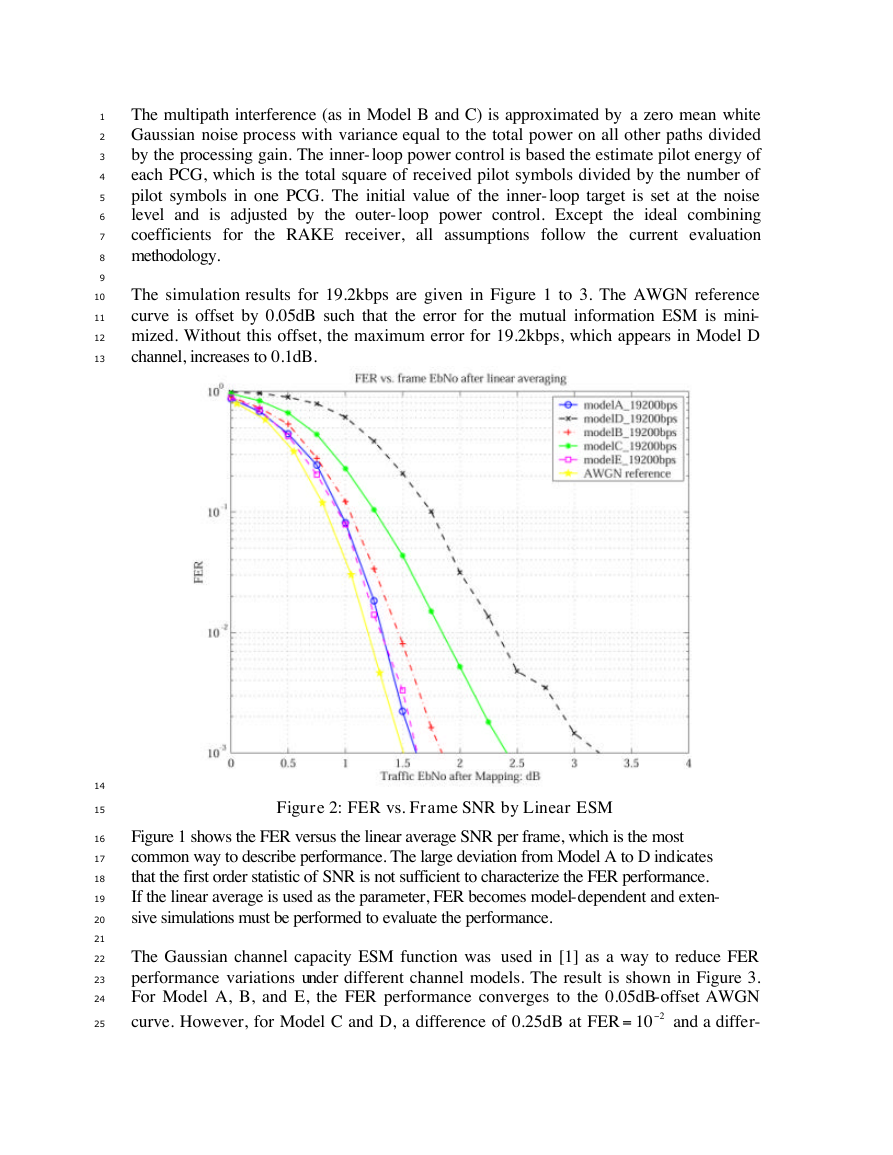
The simulation results for 19.2kbps are given in Figure 1 to 3. The AWGN reference
curve is offset by 0.05dB such that the error for the mutual information ESM is mini-
mized. Without this offset, the maximum error for 19.2kbps, which appears in Model D
channel, increases to 0.1dB.
Figure 2: FER vs. Frame SNR by Linear ESM
Figure 1 shows the FER versus the linear average SNR per frame, which is the most
common way to describe performance. The large deviation from Model A to D indicates
that the first order statistic of SNR is not sufficient to characterize the FER performance.
If the linear average is used as the parameter, FER becomes model-dependent and exten-
sive simulations must be performed to evaluate the performance.
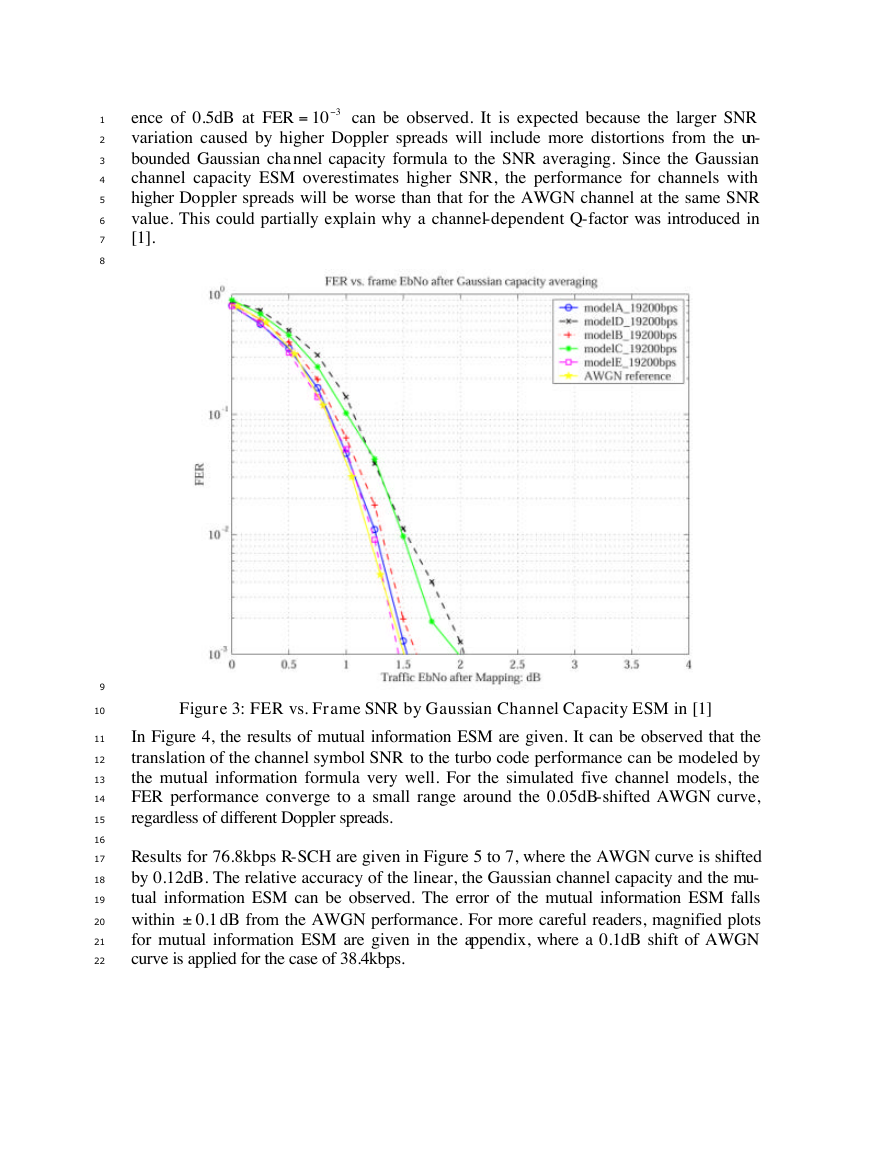
The Gaussian channel capacity ESM function was used in [1] as a way to reduce FER
performance variations under different channel models. The result is shown in Figure 3.
For Model A, B, and E, the FER performance converges to the 0.05dB-offset AWGN
and a differ-
curve. However, for Model C and D, a difference of 0.25dB at FER
210-
=
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
=
310-
ence of 0.5dB at FER
can be observed. It is expected because the larger SNR
variation caused by higher Doppler spreads will include more distortions from the un-
bounded Gaussian cha nnel capacity formula to the SNR averaging. Since the Gaussian
channel capacity ESM overestimates higher SNR, the performance for channels with
higher Doppler spreads will be worse than that for the AWGN channel at the same SNR
value. This could partially explain why a channel-dependent Q-factor was introduced in
[1].
Figure 3: FER vs. Frame SNR by Gaussian Channel Capacity ESM in [1]
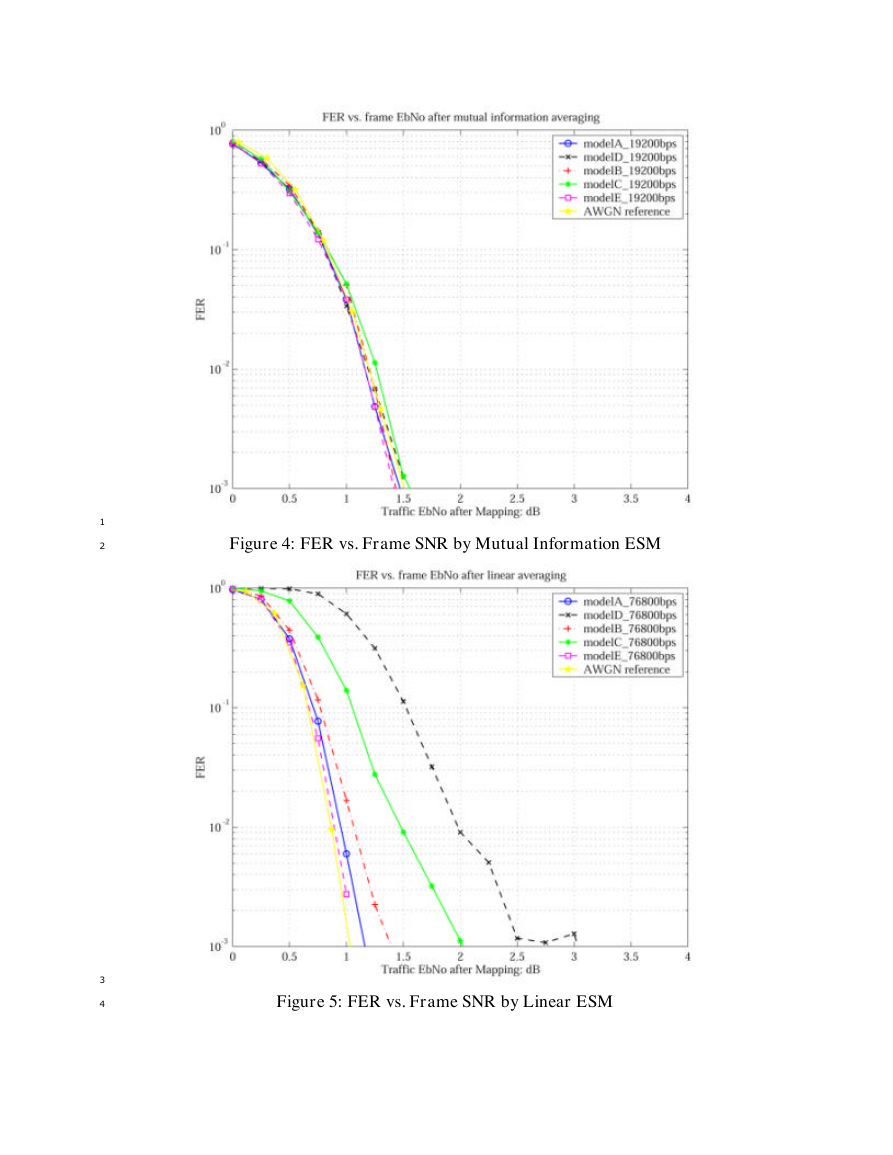
In Figure 4, the results of mutual information ESM are given. It can be observed that the
translation of the channel symbol SNR to the turbo code performance can be modeled by
the mutual information formula very well. For the simulated five channel models, the
FER performance converge to a small range around the 0.05dB-shifted AWGN curve,
regardless of different Doppler spreads.
Results for 76.8kbps R-SCH are given in Figure 5 to 7, where the AWGN curve is shifted
by 0.12dB. The relative accuracy of the linear, the Gaussian channel capacity and the mu-
tual information ESM can be observed. The error of the mutual information ESM falls
within
dB from the AWGN performance. For more careful readers, magnified plots
for mutual information ESM are given in the appendix, where a 0.1dB shift of AWGN
curve is applied for the case of 38.4kbps.
1.0–
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
1
2
3
4
Figure 4: FER vs. Frame SNR by Mutual Information ESM
Figure 5: FER vs. Frame SNR by Linear ESM
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
