logo资料库

汽车转向节静动态特性分析与多目标拓扑优化.pdf

发布时间：2022-05-29 发布人：admin 分类：说明书 资料大小：0.52M 资料格式：pdf 举报 版权申诉
第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
资料共6页，全文预览结束
    第36卷第4期 辽宁工程技术大学学报（自然科学版） 2017年4月 Vol.36 No.4 Journal of Liaoning Technical University（Natural Science） Apr. 2017 收稿日期：2015-11-16 作者简介：蒲志新（1973-），男，河北 玉田人，硕士，副教授，主要从事并联机床、并联机构和先进制造技术等方向的研究. 本文编校：焦丽 辽宁工程技术大学学报（自然科学版)网址：http://202.199.224.158/ http://xuebao.lntu.edu.cn/ 蒲志新,岳玮琦,于英华.汽车转向节静动态特性分析与多目标拓扑优化[J].辽宁工程技术大学学报(自然科学版),2017,36(4):421-426. doi:10.11956/j.issn.1008-0562.2017.04.017 PU Zhixin,YUE Weiqi,YU Yinghua. Static and dynamic characteristics analysis and multi-objective topology optimization of a steering knuckle [J].Journal of Liaoning Technical University(Natural Science),2017,36(4):421-426. doi:10.11956/j.issn.1008-0562.2017.04.017 汽车转向节静动态特性分析与多目标拓扑优化 蒲志新，岳玮琦，于英华 （辽宁工程技术大学 机械工程学院，辽宁 阜新 123000） 摘 要：为使复杂工况下运行的SUV汽车在满足各项性能要求的基础上实现轻量化，以汽车转向节为研究对象，利用变密度连续体结构拓扑优化与折衷规划法相结合来建立多目标优化函数模型，利用层次分析法确定各子目标的权重，进行多目标拓扑优化，得到了材料的理想分布.优化前后的转向节静动态特性对比分析表明，采用多目标拓扑优化方法设计的汽车转向节在轻量化的基础上提高了其结构的刚度和固有频率，实现了多目标同时优化.关键词：转向节；静动态分析；折衷规划；层次分析法；多目标拓扑优化 中图分类号：U 463.46 文献标志码：A 文章编号：1008-0562(2017)04-0421-06 Static and dynamic characteristics analysis and multi-objective topology optimization of a steering knuckle PU Zhixin, YUE Weiqi, YU Yinghua (College of Mechanical Engineering, Liaoning Technical University, Fuxin 123000, China) Abstract：In order to realize the weight-lightening of SUVs on the base of meeting each performance requirement under complex work conditions, automobile steering knuckle was studied. Topology optimization of continuum structure with variable density and compromise programming method were combined to propose a multi-objective optimization function model, and analytic hierarchy process are used to determine the relative weight of each sub target and to conduct multi-objective topology optimization. Optimization resulted in ideal distribution of materials. The comparative analysis of static and dynamic characteristics showed that the optimization improved the stiffness and natural frequency of the structure on the base of automobile weight-lightening, thus realizing the multi-objective optimization. Key words: steering knuckle; static and dynamic analysis; compromise plan; analytic hierarchy process; multi-objective topology optimization 0 引言 转向节是汽车底盘上关键安全零部件，将悬架、前车轴、转向系统和制动器有效地连接，转向节也是车辆转向系的重要部件.车辆在复杂工况行驶，转向节用于控制行驶方向，需承受来自转向器的转向力、转向轮的负载和来自道路的冲击等[1-2].实现转向节在满足强度、抗冲击性、抗疲劳强度以及可靠性方面要求的同时降低质量，属于零件结构优化问题，因此本文以某SUV汽车转向节为研究对象，运用拓扑优化方法对其结构进行优化. 目前对单目标拓扑优化的研究均局限于将零件某个性能指标作为目标函数将其最大化或最小化，得出新的结构之后再次对其他性能进行验证.考虑各指标间复杂关系，此方法很难设计出在复杂工况下各项性能指标均优的转向节，因此本文基于变密度方法应用Hypermesh软件对汽车转向节进行多目标拓扑优化[3-6].针对刚度、动态固有频率、质量三个子目标采用折衷规划法研究多目标优化问题，利用层次分析法确定各个目标权重，建立合理的多目标数学优化模型进行拓扑优化.得到既满足静刚度、质量又满足动态特征值最优的多目标拓扑优化结构模型[7-9]. 1 汽车转向节静动态分析 本文所研究的转向节为中心孔类转向节，在汽车中国煤炭期刊网 www.chinacaj.net
    辽宁工程技术大学学报（自然科学版） 第36卷 辽宁工程技术大学学报（自然科学版)网址：http://202.199.224.158/ http://xuebao.lntu.edu.cn/ 422 前模块中位置及与底盘其他零件联接情况见图1. 图1 转向节与底盘其他零部件的联接情况 Fig.1 steering knuckle connected to other parts of chassis 在Pro/Engineer软件中对汽车转向节进行建模，将简化后的汽车转向节CAD模型导入ANSYS软件进行模型载荷约束施加，见图2，并对模型进行网格化分，见图3. 图2 转向节约束 Fig.2 steering knuckle constraints 图3 转向节有限元分析模型 Fig.3 finite element analysis model of steering knuckle 1.1 转向节静态分析 本文研究的转向节材料为40Cr，密度为7.8×103kg/m3，弹性模量为206 GPa，泊松比为0.3，屈服强度为750 MPa，根据汽车整车参数，计算中所使用的各参数[10]见表1. 表1 汽车整车参数 Tab. 1 vehicle parameter table 参数 取值 整车质量(满载) G/ kg 1 645 轴距L/mm 2 670 重心到后轴距离b/mm 1 360 重心高度（满载）hg/mm 680 轮胎滚动半径r/mm 307 动载系数kd 2.65 地面附着系数ψ 0.75 侧向滑移附着系数φ 1 发生路面不平工况时汽车约束主要有减震器处、转向拉杆和下摆臂处的约束，主要受力情况是垂直方向冲击载荷；汽车在紧急制动工况时，减震器、制动器、转向拉杆和下摆臂为主要考虑的约束，主要受到收到垂直载荷、制动力作用，此外转向节还受到由于制动力的平移产生的力矩；在转弯侧滑工况时，主要约束有减震器处、转向拉杆和下摆臂处的约束，转向节主要受到垂直载荷、侧向载荷及侧向力平移产生的力矩.汽车在行驶过程中也会发生三种工况同时发生情况，此时转向节所受应力最大，也最危险.转向节受力为 gdzgddhKGuFbLgt； ,.,.XZYZYXXYFFFFMFrMFr 参照机动车制动性能规定，ddut取7.4(m/s2). 针对组合工况，将计算结果应用蒙特卡罗超拉丁抽样随机有限元法循环试验500次，置信度为95%，进行可靠性分析，输出变量为转向节的应力极限状态函数，即转向节剩余强度R=S-Q，其中S为转向节材料的屈服强度，Q为转向节所受强度.提取剩余强度抽样过程图、抽样柱状图、均值趋势图、累计分布图及转向节失效概率值分别见图4～图7.由图4～图7可得出，均值曲线逐渐收敛，趋向水平，随着循环次数的增加波动减小，蒙特卡罗循环抽样次数足够，剩余强度的柱状图与概率曲线拟合较好，光滑无间隙，抽样次数足够多.转向节在组合工况下剩余强度R的平均大小为226.16 MPa，平均应力大小为523.84 MPa，剩余强度R的最小值是74.28 MPa. 1与减震器下方 固定连接 2与减震器下方固定连接7与轮毂轴承连接 6与转向杆球头铰接5与下控制臂球头铰接 4与制动钳总成 螺栓连接 3与制动钳总成 螺栓连接 中国煤炭期刊网 www.chinacaj.net
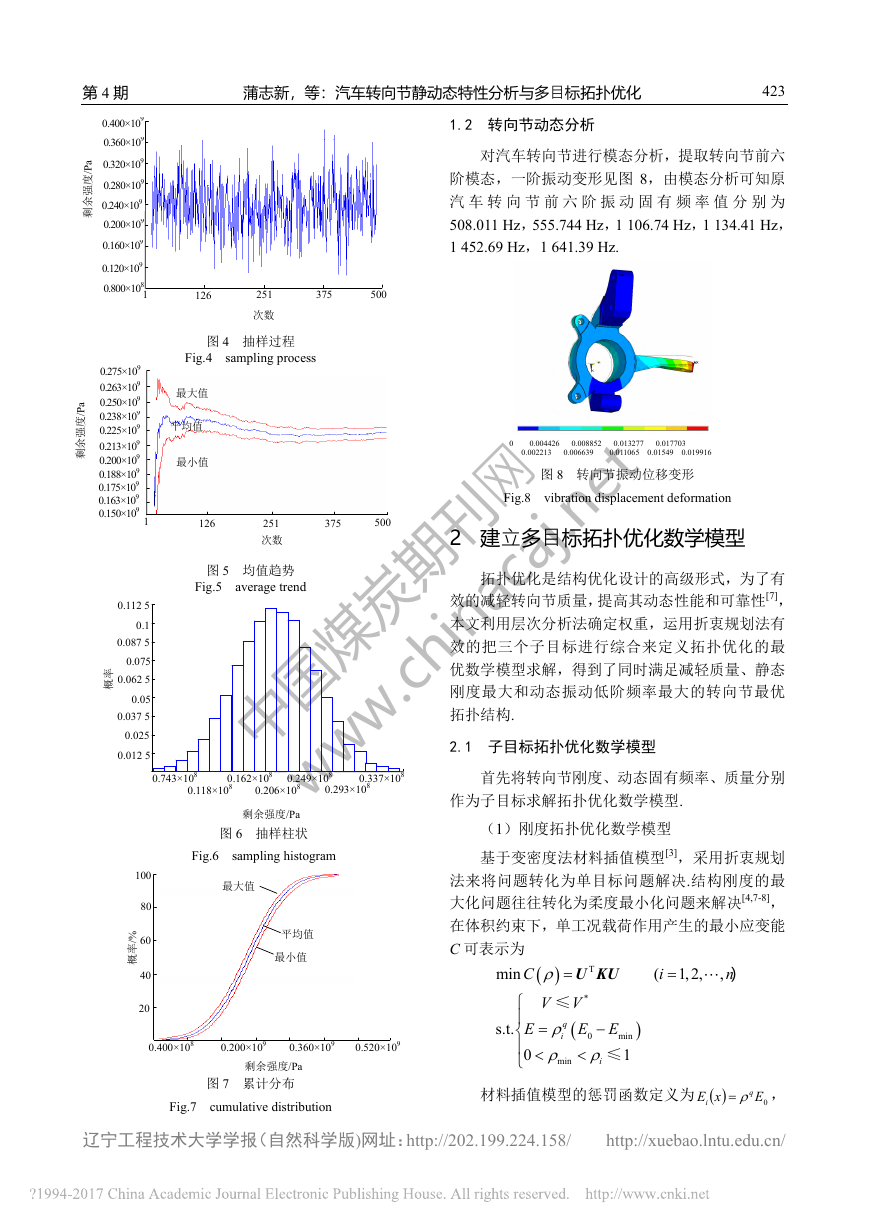
    第4期 蒲志新，等：汽车转向节静动态特性分析与多目标拓扑优化 辽宁工程技术大学学报（自然科学版)网址：http://202.199.224.158/ http://xuebao.lntu.edu.cn/ 423 图4 抽样过程 Fig.4 sampling process 图5 均值趋势 Fig.5 average trend 图6 抽样柱状 Fig.6 sampling histogram 图7 累计分布 Fig.7 cumulative distribution 1.2 转向节动态分析 对汽车转向节进行模态分析，提取转向节前六阶模态，一阶振动变形见图8，由模态分析可知原汽车转向节前六阶振动固有频率值分别为 508.011 Hz，555.744 Hz，1 106.74 Hz，1 134.41 Hz，1 452.69 Hz，1 641.39 Hz. 图8 转向节振动位移变形 Fig.8 vibration displacement deformation 2 建立多目标拓扑优化数学模型 拓扑优化是结构优化设计的高级形式，为了有效的减轻转向节质量，提高其动态性能和可靠性[7]，本文利用层次分析法确定权重，运用折衷规划法有效的把三个子目标进行综合来定义拓扑优化的最优数学模型求解，得到了同时满足减轻质量、静态刚度最大和动态振动低阶频率最大的转向节最优拓扑结构. 2.1 子目标拓扑优化数学模型 首先将转向节刚度、动态固有频率、质量分别作为子目标求解拓扑优化数学模型. （1）刚度拓扑优化数学模型 基于变密度法材料插值模型[3]，采用折衷规划法来将问题转化为单目标问题解决.结构刚度的最大化问题往往转化为柔度最小化问题来解决[4,7-8]，在体积约束下，单工况载荷作用产生的最小应变能C可表示为 T*0minminmin(1,2,,s.t.01qiiCinVVEEE≤≤）UKU 材料插值模型的惩罚函数定义为0ExEqi， 1 126 251 375 5000.800×1080.120×1090.160×1090.200×1090.240×1090.280×1090.320×1090.360×1090.400×109次数 剩余强度/Pa 1 126 251 375 5000.150×109 0.163×109 0.275×109 0.263×109 0.250×109 0.238×109 0.213×109 0.200×109 0.188×109 0.175×109 0.225×109 次数 剩余强度/Pa 剩余强度/Pa 0.743×108 0.118×108 0.162×108 0.249×108 0.337×1080.206×108 0.293×1080.012 50.0250.037 50.050.062 50.0750.087 50.10.112 5概率 0.400×108 0.200×1090.360×109 0.520×10920406080100剩余强度/Pa 概率/% 0 0.004426 0.008852 0.013277 0.017703 0.002213 0.006639 0.011065 0.01549 0.019916 最大值 平均值 最小值 最大值平均值 最小值 中国煤炭期刊网 www.chinacaj.net
    辽宁工程技术大学学报（自然科学版） 第36卷 辽宁工程技术大学学报（自然科学版)网址：http://202.199.224.158/ http://xuebao.lntu.edu.cn/ 424 式中，C(ρ)为转向节柔度值；ρ为单元密度；ρi为第i个单元密度；K、U为单元刚度和单元位移矩阵；V为汽车转向节体积分数；V*=0.3；q为惩罚因子；E为优化后的弹性模量；惩罚因子q取值为3；结构的应变能越小系统的整体刚度就越大，转向节在多工况下的刚度拓扑优化问题中，载荷工况不同对应着不同的最优拓扑结构，多刚度就对应着多目标拓扑优化，实际多工况下，以体积分数为约束条件的静态多工况刚度拓扑优化数学模型为 T12min3maxmin1min,,,=nmkkkkkkCCCCC， 式中，ωk为第k个工况的权值；Ck(ρ)为第k个工况的柔度目标函数；Ckmax为第k个工况下柔度最大值；Ckmin为第k个工况下柔度最小值. （2）动态固有频率拓扑优化数学模型 进行动态固有频率优化时，若只优化单独一个低阶频率，往往会发生模态交换现象[9]，即相邻的较高阶次特征值会降低，为了避免发生此现象，采用平均频率公式的倒数来建立固有频率拓扑优化目标函数且以体积分数为约束条件建立拓扑优化数学模型 T12111min,,,=max1nmiiiΦP 式中，Φ(ρ)为平均平率的倒数；P(ρ)为平均频率；λi为第i阶特征频率；ωi为第i阶频率的权重系数；λ、β为用来调整目标函数的参数；m为优化频率的阶次，其余参数定义与之前相同. （3）质量拓扑优化数学模型 niiiVf1min， 式中，f(ρ)为目标函数，转向节的质量；n为单元离散数；其余参数定义与之前一致. 2.2多目标拓扑优化综合数学模型 转向节结构多目标拓扑优化以体积分数作为约束条件，综合考虑静态多工况刚度、动态固有频率、质量进行优化.由带权重的折衷规划法可得到多目标拓扑优化的综合目标函数为 3min31maxmin11/333minmin3323maxminmaxminminmkkkkkkCCZCCffff， 式中，Z(ρ)为综合目标函数；γ1、γ2、γ3为柔度、固有频率、质量的权值；Φmin、Φmax、fmin、fmax分别为Φ(ρ)、f(ρ)的最小值和最大值；其余参数定义与之前相同. 2.3 子目标权重的确定 利用层次分析法确定静态刚度数学模型中三个子工况的权重ɷ1、ɷ2、ɷ3，以及综合目标函数中子目标柔度、频率、质量的权值γ1、γ2、γ3[10].在确定静态多工况刚度拓扑优化数学模型中ɷ1、ɷ2、ɷ3时，有3个子目标（路面不平M1、紧急制动M2、转弯侧滑M3）的多目标优化.设这三个子目标的重要性权重分别是α1、α2、α3.建立配对比较矩阵 111213111213212223212223313233313233mmmmmmmmm， 式中，矩阵M中元素mij（i,j=1,2,3）为子目标Mi对Mj的要性比值.然后将矩阵M右乘向量α=[α1,α2,α3]T有 T1231231230.，I 可知，矩阵M的特征向量即为向量α.求出该矩阵的最大特征值对应的特征向量，就是对应的各个子目标的重要性权重.设三个静态刚度子目标M1、M2、M3相互间两两比值分别为m12=0.8，m13=2，m23=2.5，配对比较矩阵为 10.821.2512.5.0.50.41 求出该矩阵的最大特征值对应的特征向量为α=[0.5963 0.7457 0.2981]T，即为三个子目标的重要性权重值.归一化处理后得ɷ1=0.364、ɷ2=0.455、ɷ3=0.181同样可以确定出综合目标函数中的三个子目标（柔度N1、固有频率N2、质量N3）的权重值γ1=0.333、γ2=0.5、γ3=0.167. 中国煤炭期刊网 www.chinacaj.net
    第4期 蒲志新，等：汽车转向节静动态特性分析与多目标拓扑优化 辽宁工程技术大学学报（自然科学版)网址：http://202.199.224.158/ http://xuebao.lntu.edu.cn/ 4253 汽车转向节多目标拓扑优化 3.1 转向节拓扑优化 首先在Hypermesh中前处理模块对转向节进行有限元处理，得到的有限元模型见图9，其中转向节与其他零部件连接采用rb2连接，其中紫色区域为非设计区域，黄色区域为设计区域.后利用Optistruct模块自定义本文提出的折衷规划公式为目标函数，以体积为约束使用变密度法[11].多目标拓扑优化得到的转向节拓扑结构见图10.可知单元密度小于0.505的部分被省略，单元密度大于0.505的区域被保留.在拓扑优化基础上对模型进行改进，在省略区域增加加强筋，最终修改模型见图11. 图9 分析模型 Fig.9 Analysis Model 图10 优化结构 Fig.10 optimized structure 图11 改进后转向节结构 Fig.11 improved steering knuckle simplified 3.2 转向节拓扑优化结果分析对比 经过改进以后，汽车转向节的拓扑结构发生改变.为了验证改进后的结构正确性和可靠性，对其改进的转向节进行结构分析，使其结果更具有对比性. （1）刚度对比 将改进后的转向节模型在组合工况下进行静强度可靠性分析[12]，见图12.剩余强度平均值为384.19 MPa，受力平均值为366 MPa，与原模型相比明显有所降低. 图12 组合工况下均值分布 Fig.12 combination conditions R average trend chart （2）动态固有频率对比 将改进后的转向节进行模态分析，见图13.可知改进后转向节一阶固有频率为565.041 Hz，二阶固有频率为618.169 Hz，三阶固有频率为致 1 425.9 Hz，四阶固有频率为1882.16 Hz，五阶固有频率为2 157.46 Hz，六阶固有频率为2 927.43 Hz，比原转向节各阶频率均有所增大. （3）质量对比 测得原汽车转向节质量为7.5 kg，改进后得转向节质量为7.08 kg. 图13 改进后转向节振动位移 Fig.13 vibration displacement deformation 1126251 3755000.260×1090.280×1090.460×1090.440×1090.420×1090.400×1090.360×1090.340×1090.320×1090.300×1090.380×1090 0.102 42 0.020 484 0.030 727 0.040 969 0.005 121 0.015 363 0.015 605 0.035 848 最大值平均值最小值中国煤炭期刊网 www.chinacaj.net
    辽宁工程技术大学学报（自然科学版） 第36卷 辽宁工程技术大学学报（自然科学版)网址：http://202.199.224.158/ http://xuebao.lntu.edu.cn/ 426 （4）改进后转向节疲劳寿命估计 对改进后转向节做寿命估算，通过静力学计算得出转向节在紧急制动工况下应力最大位置是在 1 886节点处，应力值为72.5 MPa.输入转向节的S-N值，建立位置、事件和载荷，存储关系位置的应力等条件，输入循环次数为107次，进行疲劳计算. 计算结果表明：改进后的转向节疲劳使用系数为0.714＜1，寿命大约为140万次满足其工程要求. 改进前后汽车转向节性能指标对比见表2.可知转向节经过多目标拓扑优化改进后满足轻量化的基础上，刚度、频率等性能指标都有所提高. 表2 优化前后性能指标对比 Tab.2 steering knuckle performance comparison before and after optimization 指标 原转向节 改进转向节 变化量/% 质量 7.5 kg 7.08 kg -5.60 固有频率 508.011Hz 565.041 Hz 11.20 最大应力值 365.81 MPa 345.39 MPa -5.58 4 结论 （1）利用Ansys软件建立了汽车转向节仿真模型，分析得到了现有汽车转向节动静态特性. （2）利用密度法与折衷规划法相结合的方式在Hypermesh中建立多目标拓扑优化数学模型，对汽车转向节进行优化. （3）在实际的组合工况下对优化后汽车转向节进行静动态分析，对比可知，优化后转向节在刚度、固有频率和质量上均有所改进且疲劳寿命满足工程要求. （4）本文深化和拓宽了汽车转向节设计优化理论，推动产品设计优化由传统经验设计优化转向现代数字设计的进程，对实现汽车轻量化具有重要的现实意义. 参考文献： [1] 董立立,朱煜,牛小铁,等.超精密机械结构多目标拓扑优化设计[J].中国机械工程,2010(7):761-765. DONG Lili,ZHU Yu,NIU Xiaotie,et al.Multi-objective topological optimization design of ultra-precision mechanical structure[J].China Mechanical Engineering,2010(7):761-765. [2] GAO Yunkai,MENG Dejian,JIANG Xin.Topology optimization analysis for modifying body structure of electric car[J].China Mechanical Engineering,2006,17(23):2 522-2 525. [3] MARLER R T,ARORA J S.Survey of Multi-objective Optimization, Methods for Engineering[J].Structural and Multidisciplinary Optimization, 2004,26(6):369-395. [4] 蒋金星,谷正气,米承继,等.矿用自卸车车架结构多目标拓扑优化研究[J].中国机械工程,2013(8):1 028-1 032. JIANG Jinxing,GU Zhengqi,MI Chengji,et al.Multi-objective topology optimization of a mining dump truck frame[J].China Mechanical Engineering,2013(8):1 028-1 032. [5] 方子帆,杨磊,杜道佳,等.支撑结构多目标拓扑优化设计研究[J].中国机械工程,2010,21(15):1 836-1 839. FANG Zifan,YANG Lei,DU Daojia,et al.Research on topology optimization design for support structure[J].Chinese Internal Combustion Engine,2010,21(15):1 836-1 839. [6] 张胜兰,郑冬黎,郝琪,等.基于Hyperworks的结构优化技术[M].北京:机械工业出版社,2007. [7] 蒋大伟,芮执元.控制臂多目标拓扑优化研究[J].机械强度,2014(3): 408-412. JIANG Dawei,RUI Zhiyuan..Research on multi-objective topology optimization for control arm[J].Journal of Machanical Strength,2014(3): 408-412. [8] FAN Hongjun,LIU Tieying.Risk-based multiobjective optimization method of bridge maintenance strategies[J].Transport Standardization, 2009(10):83-87. [9] 占金青,张宪民.连续体结构的静动态多目标拓扑优化方法研究[J]. 机械强度,2010(6):933-937. ZHAN Jinqing,ZHANG Xianmin.Research on Static and dynamic multi-objective topology optimization of continuum structures[J]. Journal of Mechanical Strength,2010(6):933-937. [10] 蔡卫,吴兵.层次分析法在矿井通风评价中的应用[J].辽宁工程技术大学学报(自然科学版),2005,24(2):149-152. CAI Wei,WU Bing.Application of analytic hierarchical process in mine ventilation evaluation[J].Journal of Liaoning Technical University: (Natural Science),2005,24(2):149-152. [11] ZHANG Huailang,ZHU Wenzhe,CHEN Zhengjie.study on intensity analysis of heavy dump truck frame[J].Journal of Guangxi University (Natural Science Edition),2008,33(4):387-390. [12]吴丽娟,赵丽娟,李柳.海量空间数据点四边形网格优化[J].辽宁工程技术大学学报(自然科学版),2009,28(1):49-51. WU Lijuan,ZHAO Lijuan,LI Liu.Optimization of quadrangular meshes based on cloud data[J].Journal of Liaoning Technical University (Natural Science),2009,28(1):49-51. 中国煤炭期刊网 www.chinacaj.net
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料