凸优化及其在信号处理中的应用导引--苏文藻.pdf

发布时间：2022-06-09 发布人：admin 分类：说明书资料大小：2.50M 资料格式：pdf 举报版权申诉

tianlan1002-10461008-4744302543287548945.pdf-第1页.png

第1页 / 共209页

tianlan1002-10461008-4744302543287548945.pdf-第2页.png

第2页 / 共209页

tianlan1002-10461008-4744302543287548945.pdf-第3页.png

第3页 / 共209页

tianlan1002-10461008-4744302543287548945.pdf-第4页.png

第4页 / 共209页

tianlan1002-10461008-4744302543287548945.pdf-第5页.png

第5页 / 共209页

tianlan1002-10461008-4744302543287548945.pdf-第6页.png

第6页 / 共209页

tianlan1002-10461008-4744302543287548945.pdf-第7页.png

第7页 / 共209页

tianlan1002-10461008-4744302543287548945.pdf-第8页.png

第8页 / 共209页

文本预览

Convex Optimization and Its Applications in Signal Processing Anthony Man-Cho So Department of Systems Engineering & Engineering Management The Chinese University of Hong Kong Hong Kong ChinaSIP 2014 Tutorial, July 9, 2014

• The main references of this tutorial: Z.-Q. Luo, W.-K. Ma, A. M.-C. So, Y. Ye, & S. Zhang, “Semideﬁnite relaxation of quadratic optimization problems,” IEEE Signal Process. Mag., May 2010. S. Cui, A. M.-C. So, & R. Zhang, “Unconstrained & constrained optimization problems,” Chapter 14 of Mathematical Foundations for Signal Processing, Communications, and Networking, CRC Press, 2012. [Zhi-Quan Luo, Wing-Kin Ma, Anthony Man-Cho So, Yinyu Ye, and Shuzhong Zhang] [VOLUME 27 NUMBER 3 MAY 2010] [From its practical deployments and scope of applicability to key theoretical results] In recent years, the semidefinite relaxation (SDR) technique has been at the center of some of very exciting developments in the area of signal processing and communications, and it has shown great signifi- cance and relevance on a variety of applications. Roughly speak- ing, SDR is a powerful, computationally efficient approximation technique for a host of very difficult optimization problems. In particular, it can be applied to many nonconvex quadratically constrained quadratic programs (QCQPs) in an almost mechanical fashion, including the following problem: min x [ Rn s.t. xTCx xTF i x $ gi, i 5 1, c, p, xTH x 5 li, i i 5 1, c, q, (1) 1, c, Fp, H 1, c, Hq are where the given matrices C, F assumed to be general real symmetric matrices, possibly indefinite. The class of nonconvex QCQPs (1) captures many problems that are of interest to the signal process- ing and communications community. For instance, con- sider the Boolean quadratic program (BQP) min x [ Rn s.t. xT Cx 2 5 1, i 5 1, c, n. xi (2) The BQP is long known to be a computationally difficult prob- lem. In particular, it belongs to the class of NP-hard problems. Nevertheless, being able to handle the BQP well has an enormous impact on multiple-input, multiple-output (MIMO) detection and multiuser detection. Another important yet NP-hard problem in the nonconvex QCQP class (1) is Digital Object Identifier 10.1109/MSP.2010.936019 © BRAND X PICTURES IEEE SIGNAL PROCESSING MAGAZINE [20] MAY 2010 1053-5888/10/$26.00©2010IEEE A. M.-C. So, Convex Optimization and Its Applications, ChinaSIP 2014 Tutorial 1

• Acknowledgment: Shuguang Cui, Tom Luo, Wing-Kin (Ken) Ma, Yinyu Ye, Rui Zhang, & Shuzhong Zhang for co-authoring the above articles; Qiang Li, Jiaxian Pan, Xiaoxiao Wu & Xiao Fu for helping prepare this slides. • A good part of this tutorial is based the one given in ICASSP 2014 with Ken Ma. A. M.-C. So, Convex Optimization and Its Applications, ChinaSIP 2014 Tutorial 2

Outline • Part I: Crash course on convex analysis and convex optimization • Part II: Quadratically constrained quadratic programs and semideﬁnite programming • Part III: Semideﬁnite relaxation: Theory, and implications in practice • Part IV: Applications and latest advances – A. transmit beamforming – B. advanced topics in transmit beamforming – C. sensor network localization • Conclusion A. M.-C. So, Convex Optimization and Its Applications, ChinaSIP 2014 Tutorial 3

Part I: Crash Course on Convex Analysis and Convex Optimization A. M.-C. So, Convex Optimization and Its Applications, ChinaSIP 2014 Tutorial 4

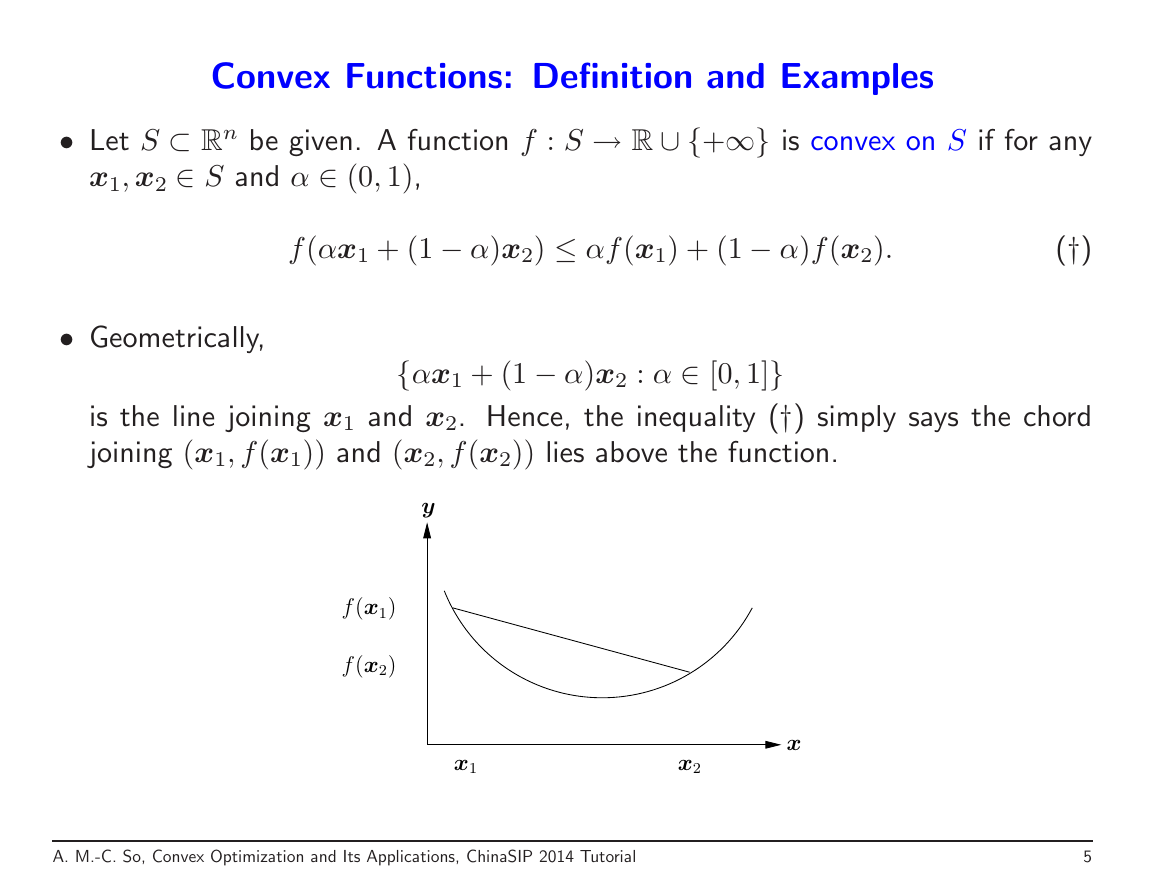
Convex Functions: Deﬁnition and Examples • Let S ⊂ Rn be given. A function f : S → R ∪ {+∞} is convex on S if for any x1, x2 ∈ S and α ∈ (0, 1), f (αx1 + (1 − α)x2) ≤ αf (x1) + (1 − α)f (x2). (†) • Geometrically, {αx1 + (1 − α)x2 : α ∈ [0, 1]} is the line joining x1 and x2. Hence, the inequality (†) simply says the chord joining (x1, f (x1)) and (x2, f (x2)) lies above the function. y f (x1) f (x2) x1 x2 x A. M.-C. So, Convex Optimization and Its Applications, ChinaSIP 2014 Tutorial 5

Convex Functions: Deﬁnition and Examples Some examples of convex functions: • Any aﬃne function f : Rn → R; i.e., f (x) = aT x + b for some a ∈ Rn and b ∈ R. • Any norm k · k on Rn. – This follows from the triangle inequality. i=1 αifi(x) for any α1, . . . , αm ≥ 0. • Any non-negative combination of convex functions f1, . . . , fm : S → R; i.e., f (x) =Pm • Let S ⊂ Rn be a convex set; i.e., for any x1, x2 ∈ S and α ∈ (0, 1), we have αx1 + (1 − α)x2 ∈ S. Then, the indicator function 1S : Rn → R ∪ {+∞} of S, which is given by 1S(x) = 0 if x ∈ S, +∞ otherwise, is convex on Rn. A. M.-C. So, Convex Optimization and Its Applications, ChinaSIP 2014 Tutorial 6

Convex Functions: Deﬁnition and Examples • Sometimes it is diﬃcult to establish the convexity of a function directly from matrices, convex on Rn? the deﬁnition. – Is Rn ∋ x 7→ xT Ax, where A ∈ Sn and Sn is the set of n× n real symmetric – Is Rm×n ∋ X 7→ σ1(X), where σ1(X) is the largest singular value of the ++ ⊂ Sn is the set of n × n positive – Is Sn matrix X, convex on the set of m × n matrices Rm×n? deﬁnite matrices, convex on Sn ++ ∋ X 7→ − log det X, where Sn ++? • It would be good to have some alternative, hopefully easier, ways to establish the convexity of a given function. A. M.-C. So, Convex Optimization and Its Applications, ChinaSIP 2014 Tutorial 7

分享到：

赞收藏

资料库

凸优化及其在信号处理中的应用导引--苏文藻.pdf

相关推荐

课程资源

热门标签

最新资料