[1993 TC]Interpolation in Digital Modems—Part I： Fundamentals.pdf

发布时间：2022-06-09 发布人：admin 分类：说明书资料大小：0.65M 资料格式：pdf 举报版权申诉

qinxi-5630321-16359647522849017587.pdf-第1页.png

第1页 / 共7页

qinxi-5630321-16359647522849017587.pdf-第2页.png

第2页 / 共7页

qinxi-5630321-16359647522849017587.pdf-第3页.png

第3页 / 共7页

qinxi-5630321-16359647522849017587.pdf-第4页.png

第4页 / 共7页

qinxi-5630321-16359647522849017587.pdf-第5页.png

第5页 / 共7页

qinxi-5630321-16359647522849017587.pdf-第6页.png

第6页 / 共7页

qinxi-5630321-16359647522849017587.pdf-第7页.png

第7页 / 共7页

文本预览

IEEE TRANSACTIONS ON COMMUNICATIONS, VOL. 41, NO. 3, MARCH 1993 501 Interpolation in Digital Modems-Part I: Fundamentals Floyd M. Gardner, Fellow, IEEE Abstrucf- Timing adjustment in a digital modem must be performed by interpolation if sampling is not synchronized to the data symbols. This paper describes the fundamental equation for interpolation, proposes a method for control, and outlines the signal-processing characteristics appropriate to an interpolator. The material combines a review of previously known topics, presentation of new results, and a tutorial exposition of the subject. A companion paper will treat performance and implementa- tion. T the symbols of the incoming data signal. In analog- IMING in a data receiver must be synchronized to I. INTRODUCTION implemented modems, synchronization typically is performed by a feedback loop that adjusts the phase of a local clock, or by a feedforward arrangement that regenerates a timing wave from the incoming signal. The local clock or the timing wave is used to sample (or strobe) the filtered output of the modem, once per symbol interval. Message data are recovered from the strobes. Timing of the strobes is adjusted for optimum detection of the symbols. Implementation of the modem by digital techniques (a topic of intense present activity) introduces sampling of the signal. In some circumstances, the sampling can be synchronized to the symbol rate of the incoming signal; see Fig. l(a) and (b). Timing in a synchronously sampled modem can be recovered in much the same ways that are familiar from analog practice. In other circumstances, the sampling cannot be synchronized to the incoming signal. Examples include 1) digital processing of unsynchronized frequency-multiplexed signals, or 2) non- synchronized digital capture and subsequent postprocessing of a signal. For one reason or another, the sampling clock must remain independent of the symbol timing. See Fig. l(c) for a nonsynchronized-sampling configuration. How is receiver timing to be adjusted, by digital methods, when it is not possible to alter the sampling clock? One answer is to interpolate among the nonsynchronized samples in such manner as to produce the correct strobe values at the modem Paper approved by the Editor for Synchronization and Optical Detection of the IEEE Communication Society. Manuscript received December 6, 1990; revised May 23, 1991. This work was supported under Contract 8022/88/NL/DG by the European Space Agency, Noordwijk, The Netherlands. This paper was presented at the Second International Workshop on Digital Signal Processing Techniques Applied to Space Communications (DSP’90), Politecnico di Torino, Turin, Italy, September 24-25, 1990. m e author is with Gardner Research Company, Palo Alto, CA 94301, IEEE Log Number 9208042. SIGNAL IN DATA OUT PROCESSOR ANALOG PROCESSOR DIGITAL SAMPLER 0 . ANALOG RECOYCRY SIGNAL IN DIGITAL . + ANALOG DATA OUT PROCESSOR - w SAMPLING @--I TIMING CONTROL PROCESSOR PROCESSOR DATA OUT PROCESSOR DIGITAL SIGNAL IN SAMPLER ANALOG b. HYBRID RECOVERY CLOCK C. DIGITAL RECOVERY Fig. 1. Timing SAMPLING N CLOCK recovery methods. TIMING CONTROL output-the sampling had been synchronized to the symbols. same strobe values that would occur if the original Interpolation is a timing-adjustment operation on the signal, not on a local clock or timing wave. In this respect, it is radically different from timing adjustment in the better- known analog modems. Of all the operations in a digitally implemented modem, interpolation is perhaps the one with the least resemblance to established analog methods. Several issues arise as follows. -What mathematical model of interpolation can be de- vised? -How -What modems? is interpolation to be controlled? characteristics are desirable in an interpolator for -How -What is the interpolator to be implemented? performance can be obtained? How large is the computing burden? conceptual model is appropriate for interpolation? -What These are the matters treated in this paper and its ‘Ompanion [l]. The first three issues are addressed here in Part I, and the last three in Part 11 [I]. Attention is concentrated On high- ‘peed methods, defined by a hardware-imposed constraint that no clock frequency can greatly exceed the signal sample rate. 027&0062/93$03.00 0 1993 IEEE

502 IEEE TRANSACTIONS ON COMMUNICATIONS, VOL. 41, NO. 3, MARCH 1993 11. BACKGROUND Interpolation as a Digital Signal Processing (DSP) opera- tion has been covered extensively in the literature; excellent examples and further references may be found in [2] and [3]. By contrast, the role of interpolation in timing adjustment has had comparatively meager attention [2, ch. 61, [4], [5]. In fact, these latter references do not speak of “interpolation”, but of “digital phase shifting” [2, ch. 61 and [4], or of “sampling-rate conversion” [2, ch. 21 and [5]. It will be seen presently that the process of timing adjust- ment includes substantially more than interpolation alone and that “rate conversion” is a more accurate label. Nonetheless, we will apply the term “interpolation” to denote all of the processes that are involved in adjustment of timing. The term “interpolation” to describe the entire timing- adjustment process appears to have been published first by a group at the Technical University of Aachen [6], [7]. The term is also used by Bingham [8, p. 1671. In light of the extensive DSP literature on interpolation, and of the large number of digitally implemented modems that have been built for voice-frequency telephone-line service, how is it that the literature on digital timing adjustment is so sparse? Authors in the established DSP literature almost invariably restrict themselves to sampling-rate conversion by a rational factor, which can be modeled as a cascade of interpolation and decimation, each by integer ratios. Thus, the output is synchronized to the input. But the inherent problem of fully digital timing adjustment is that the signal sampling is not synchronized to the symbol timing; the two rates are incommensurate and the sample times never coincide exactly with desired strobe times. Recognition of incommensurability is vital to understanding the timing- adjustment problem. Limitations of the DSP literature aside, why didn’t the timing adjustment problem arise more clearly in the design of digitally implemented telephone-line modems? The answer is that it indeed did arise, and was solved by the adaptive equalizers that play so large a role in those modems. Besides correcting for transmission dispersion, an equalizer almost incidentally also corrects the timing. For that reason, timing adjustment itself does not appear as a widely recognized, distinct problem in the context of telephone-line modems. Digital implementation is now coming to higher speed com- munications links which do not require adaptive equalization. The need for digital timing adjustment must be faced by itself, without embedding it inside an equalizer. 111. MODEL A. Timing Loop Consider the feedback timing recovery of Fig. 2. (Feedfor- ward interpolation is also feasible, but not considered here.) A time-continuous, PAM signal z(t) is received. Symbol pulses in z ( t ) are uniformly spaced at intervals T . For simplicity, z ( t ) is assumed to be a real, baseband signal, but those restrictions can be removed without difficulty. 1 SAMPLE & I CLOCK FIXED I TIMING ERROR DETECTOR Fig. 2. Elements of digital timing recovery. Assume ~ ( t ) to be bandlimited so that it can be sampled at a rate l/Ts without aliasing. If z(t) is not adequately bandlimited, aliasing will introduce distortion that causes a performance penalty. Interpolation is not an appropriate technique to be applied to wide-band signals. Samples z(mT,) = z(m) are taken at uniform intervals T,. The ratio T/Ts is assumed to be irrational, as indeed will be true in all practical situations where the symbol timing is derived from a source that is independent of the sampling clock. These signal samples are applied to the interpolator, which computes interpolants, designated y(lcTi) = y(k) at intervals Ti. We assume that Ti = T / K where K is a small integer. The data filter employs the interpolants to compute the strobes that are used for data and timing recovery. In the sequel, the interval Ti between interpolants is treated as a constant, for simplicity of explanation. A practical modem must be able to adjust the interval so that the strobes can be brought into synchronism with the data symbols of the signal; thus, the interpolation interval cannot be constant. All elements within the feedback loop contribute to the synchronization process. Timing error is measured by the tim- ing error detector and filtered in the loop filter, whose output drives the controller. The interpolator obtains instructions for its computations from the controller. This paper concentrates on the interpolator and controller alone, with little or no consideration of the data filter, the timing error detector, or the loop filter. One example of digital timing-error detectors may be found in [9], which also has references to other examples. An illustrative loop design and simulation may be found in Part I1 [l]. The data filter is shown within the feedback loop, after the interpolator. That placement is not essential; the data filter could be outside of the loop, prior to the interpolator. A data filter inside the feedback loop introduces delay, with adverse influence on loop stability. Post placement may be advantageous when the data filter is more complicated than the interpolator-a likely situa- tion-and when a relatively high sampling rate is employed for interpolation. With postplacement, the data filter can decimate its output to the required strobe rate (just one or two samples per symbol) and thereby save on computing burden. If the data filter is placed before the interpolator, then the sample rate out of the data filter must be maintained high enough to avoid aliasing. On the other hand, simulation results [ l ] indicate that quite modest sampling rates provide excellent results, even

GARDNER: INTERPOLATION IN DIGITAL MODEMS-PART I 503 Analog Impulses Analog Interpolated Signal Samples x h T s ) c DAC Interpolants c Y(kTi ) Froctionol INPUT SAMPLE TIMES Rerample at t = kTi (k-l)T; / '" brepoint Index OUTPUT SAMPLE IlYES (k+l)T; Fig. 4. Sample time relations. Fig. 3. Rate conversion with time-continuous filter. with very simple interpolators. Thus, post placement may not often be necessary. B. Interpolator Equations To derive a model for the interpolator, we recapitulate the fundamental development of Crochiere and Rabiner [2, ch. 21. The same basis underlies the adaptive rate convertor in [5]. Refer to Fig. 3, which shows a fictitious, hybrid ana- loddigital method of rate conversion. Convert the samples to a sequence of weighted analog impulses, which are applied to a time-continuous, analog, interpolating filter with impulse response hI(t). The time-continuous output of the filter is Observe that y(t)#z(t). There is no attempt, and no need to recover the original waveform, contrary to most conventional interpolation. Since a modem is required to perform filtering of signals there is no reason why some of the filtering cannot be included in the interpolator. Now resample y(t) at time instants t = kTi where Ti is synchronized with the signal symbols. In general, T;/T, is irrational; the sampling and symbol rates are incommensurate. represented by The new samples-the interpolants-are y(kT;) = E z ( m T , ) h I ( k T i - mT,). (2) m Although the model includes a fictitious DAC and a fictitious analog filter, the interpolants in (2) can be computed entirely digitally from knowledge of 1) the input sequence {z(m)}, 2) the impulse response hl(t) of the interpolating filter, and 3 ) the time instants mT, and kTi of the input and output samples. These digitally computed interpolants have identically the same values as if the analog operations had been performed. A more useful format is obtained by rearranging the index- ing in (2). Recognizing that m is a signal index, define a filter index z = int[kTi/T,] - m (3) where int[z] means largest integer not exceeding z. Also, define a basepoint index and a fractional interval where 0 5 ,c& < 1. Timing relations are illustrated in Fig. 4. Function arguments in (2) become m = m k - i and (kT; - mT,) = (z + pk)T,, and the interpolant is computed at time kT; = (mk + pk)Ts. Equation (2) can be rewritten as Equation (6) is the foundation of digital interpolation in modems. If the interpolating filter has finite impulse response (FIR), then I1 and 12 are fixed, finite numbers and the digital filter actually used for computing the interpolants has I = 12 -11 + 1 taps. At this point, most DSP accounts of interpolation assume that the ratio Ti/T, is rational. No such assumption will be made here; real-world symbol rates are almost never synchronous with independent, fixed-rate sampling clocks. Assuming a commensurate ratio tends to obscure broader issues of control and implementation. When Ti is incommensurate with T,, the fractional interval p k will be irrational and will change for each interpolant. If determined to infinite precision, PI, takes on an infinite number of values, which never repeat exactly. This behavior is contrary to that observed if Ti is assumed very nearly equal to T,-if sampling is nearly synchronized. Then fik changes only very slowly; if p k is quantized, it might remain constant over many interpolations. If T, were commensurate with Ti, but not equal, then jLk would cyclicly repeat a finite set of values, when the timing loop is in equilibrium. IV. CONTROL Fig. 5 presents the timing loop of Fig. 2 with expanded detail for the controller. The interpolator performs the computations of (6). The controller provides the interpolator with infor- mation needed to perform the computations. Other essential elements in the loop will not be treated here. An interpolant is computed from (6) using I adjacent samples z(m) of the signal and I samples of the impulse response hI(t) of the interpolating filter. The correct set of signal samples is identified by the basepoint index mk and the correct set of filter samples is identified by the fractional interval p k . Thus, the controller of Fig. 5 is responsible for determining mk and pk, and making that information available to the interpolator. Once mk and p k have been identified by the controller, then other elements load the selected signal and impulse-response

504 IEEE TRANSACTIONS ON COMMUNICATIONS, VOL. 41, NO. 3, MARCH 1993 I - , ................. ................................................... C O N R O U t R Fig. 5. Timing processor. I 1- 0 samples into the interpolation filter structure for computations. These loading operations are regarded as part of the filter implementation; some options are examined in Part I1 [ 13. The necessary control can be provided by a number- controlled oscillator (NCO). Assume that the signal samples are uniformly clocked through a shift register at rate l/Ts -and that the NCO is clocked at a rate synchronized to l / T s . Provided that the interpolator is never called upon to per- form upsampling’ then the NCo ‘lock period can be Ts‘ If upsampling is ever required, then a higher NCO clock rate is needed. Further discussion will concentrate on NCO clocking at rate l/Ts (downsampling only); modifications needed to accommodate upsampling are readily devised once the basic principles are established. The NCO is operated so that its average period is T,. Recycling of the NCO register indicates that a new interpolant is to be computed, using the signal samples currently residing in the interpolator’s shift register. Thus, basepoint index is identified by flagging the correct set of signal samples, rather than explicitly computing mk. A. Extraction of / l k Fractional interval lLk can be calculated from the contents of the NCO’s register upon recycling, as will now be explained. Designate the NCO register contents computed at the mth clock tick as q(m), and the NCO control word as W ( m ) . Then the NCO difference equation is ( 1 [a positive ~ control word ~ ~ ( m ) = [q(m - 1) - W ( m - l)]mod-1. (7) (A decrementing NCO is employed because it affords a minor simplification in computation of /Lk as compared to an incrementing NCO.) ( ~ is adjusted by the timing-recovery loop so that output of the data filter is strobed at near-optimal timing. Under loop equilibrium conditions, ~ will be nearly constant. Contents of the NCO register (also a positive fraction) will be decremented by an amount W ( m ) each Ts seconds and the register will underflow each l / W ( m ) clock ticks, on average. Thus, the NCO period is T, = T s / W ( m ) and so 1 TS W(m,) E -. T, (8) I .................... r l ( m k i l ) - r (m kt I Fig. 6. NCO relations. That is to say, W ( m ) is the synchronizer’s estimate of the average frequency of interpolation l/T,, expressed relative to the sampling frequency l / T s . The control word is an estimate because it is produced from filtering of multiple, noisy measurements of timing error. 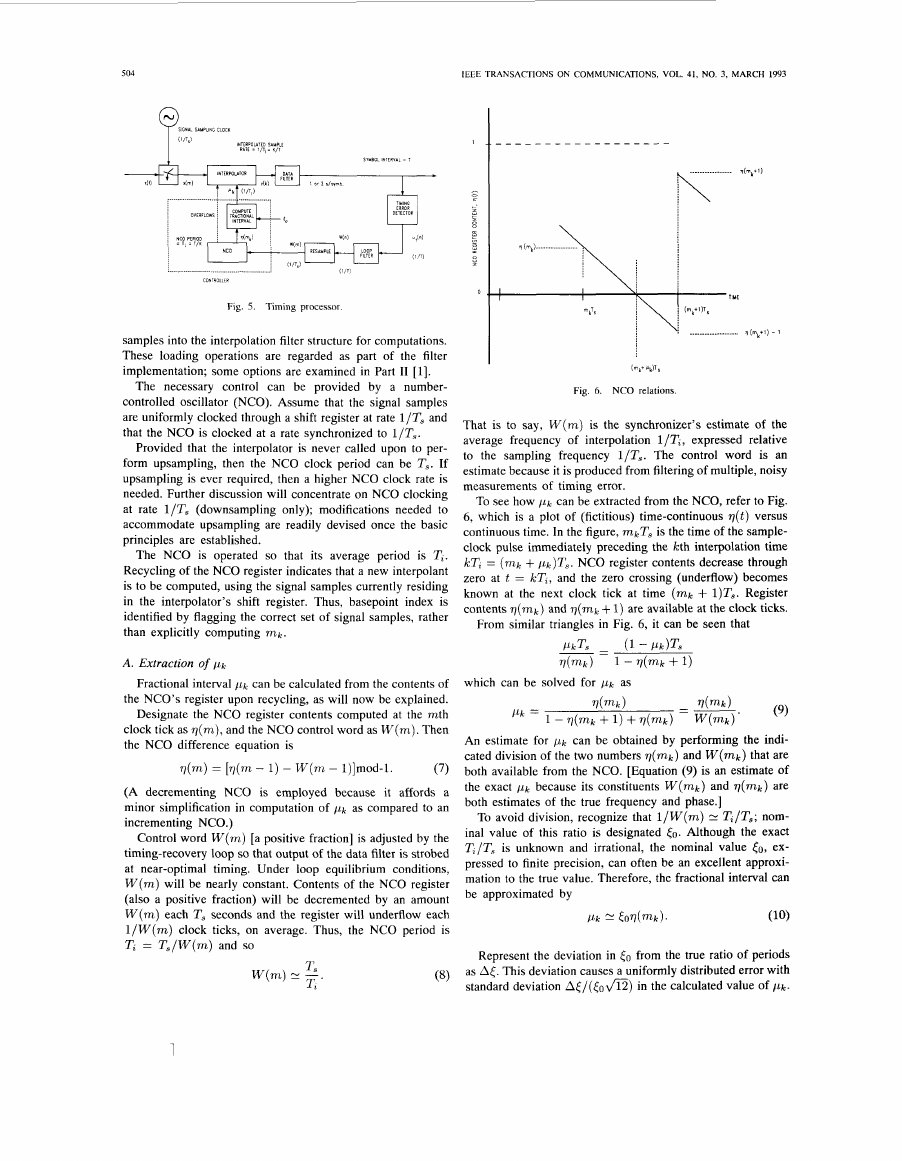To see how / L k can be extracted from the NCO, refer to Fig. 6, which is a plot of (fictitious) time-continuous q(t) versus continuous time. In the figure, mkTs is the time of the sample- clock pulse immediately preceding the kth interpolation time ICT, = ( m k + pk)TS. NCO register contents decrease through zero at t = ICT,, and the zero crossing (underflow) becomes known at the next clock tick at time ( m k + l)Ts. Register contents q ( m k ) and q ( m k + 1) are available at the clock ticks. From similar triangles in Fig. 6, it can be seen that /IkTs - (1 -Pk)Ts - - ‘V(mk) 1 - V(m,k f 1 ) which can be solved for pk as /Lk = 1 - q(mk + 1 ) + q(mk) - w ( m k ) V ( m k ) - An estimate for P k can be obtained by performing the indi- cated division of the two numbers q ( m k ) and W(mk) that are both available from the NCO. [Equation (9) is an estimate of the exact /Lk because its constituents W(mk) and q ( m k ) are ’0th estimates of the true frequency and phase.] To avoid division, recognize that l / W ( m ) 2~ T,/Ts; nom- inal value of this ratio is designated to. Although the exact / T ~ is unknown and (09 ex- pressed to finite precision, can often be an excellent approxi- mation to the true value. Therefore, the fractional interval can be approximated by the P k E EOQ(mk). (10) Represent the deviation in Eo from the true ratio of periods as A[. This deviation causes a uniformly distributed error with standard deviation A [ / ( [ o O ) in the calculated value of p k .

GARDNER: INTERPOLATION IN DIGITAL MODEMCPART I If the deviation of [ O is too large, then a first order correction reduces the standard deviation in pk to at2/([;fi), again without requiring a division. Timing errors arising from multiplying by the nominal

506 IEEE TRANSACTIONS ON COMMUNICATIONS, VOL. 41, NO. 3, MARCH 1993 0 ) Spectrum of x(t) b) Spectrum of x(mT,) c) Spectrum of y(t) d) Folded Spectrum of y(kTi) Fig. 7. Signal spectra. behavior is desirable in a practical interpolation filter. Of course, no realizable filter can provide infinite attenuation over an entire stopband. Therefore, any practical filter will introduce some penalty because of incomplete suppression of images. 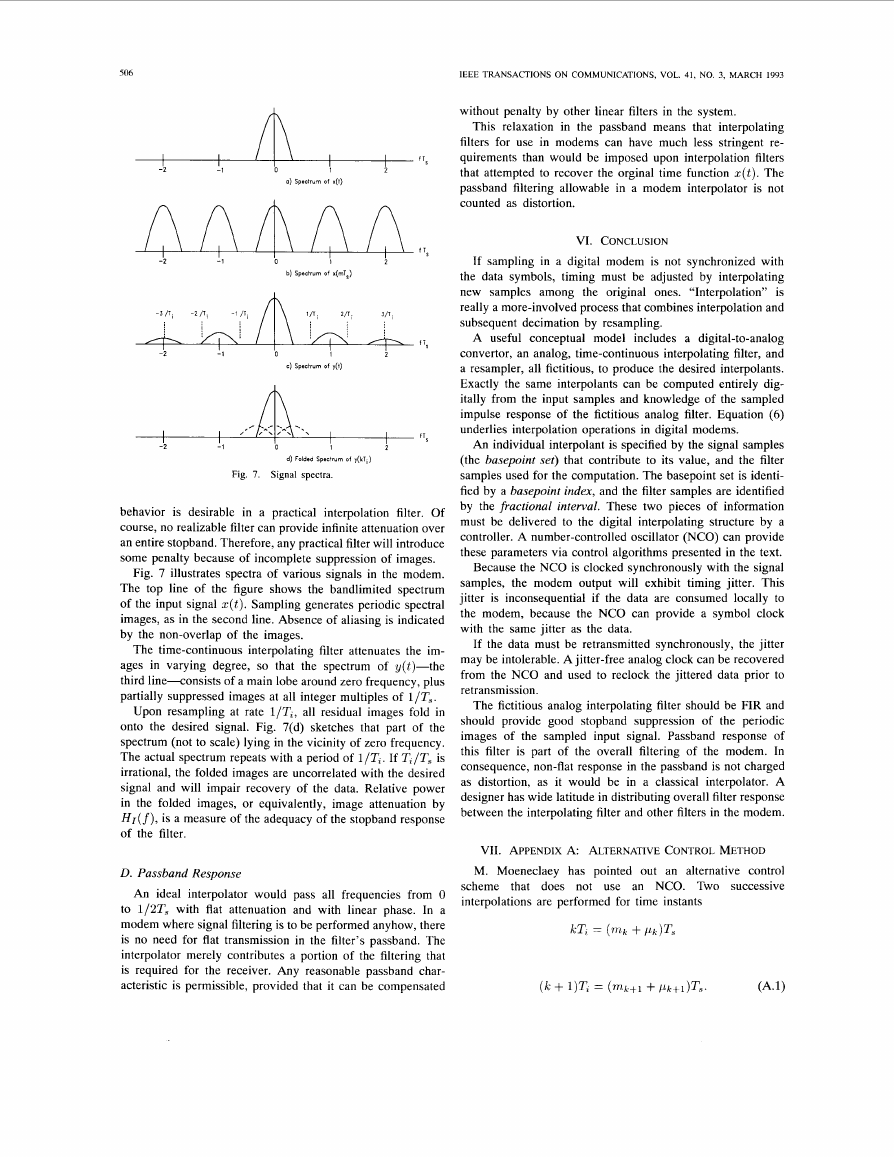Fig. 7 illustrates spectra of various signals in the modem. The top line of the figure shows the bandlimited spectrum of the input signal ~ ( t ) . Sampling generates periodic spectral images, as in the second line. Absence of aliasing is indicated by the non-overlap of the images. The time-continuous interpolating filter attenuates the im- ages in varying degree, so that the spectrum of y(t)-the third line-consists of a main lobe around zero frequency, plus partially suppressed images at all integer multiples of l/Ts. Upon resampling at rate l/Ti, all residual images fold in onto the desired signal. Fig. 7(d) sketches that part of the spectrum (not to scale) lying in the vicinity of zero frequency. The actual spectrum repeats with a period of l/Ti. If T,/T, is irrational, the folded images are uncorrelated with the desired signal and will impair recovery of the data. Relative power in the folded images, or equivalently, image attenuation by H r ( f ) , is a measure of the adequacy of the stopband response of the filter. without penalty by other linear filters in the system. This relaxation in the passband means that interpolating filters for use in modems can have much less stringent re- quirements than would be imposed upon interpolation filters that attempted to recover the orginal time function ~ ( t ) . The passband filtering allowable in a modem interpolator is not counted as distortion. VI. CONCLUSION If sampling in a digital modem is not synchronized with the data symbols, timing must be adjusted by interpolating new samples among the original ones. “Interpolation” is really a more-involved process that combines interpolation and subsequent decimation by resampling. A useful conceptual model includes a digital-to-analog convertor, an analog, time-continuous interpolating filter, and a resampler, all fictitious, to produce the desired interpolants. Exactly the same interpolants can be computed entirely dig- itally from the input samples and knowledge of the sampled impulse response of the fictitious analog filter. Equation (6) underlies interpolation operations in digital modems. An individual interpolant is specified by the signal samples (the basepoint set) that contribute to its value, and the filter samples used for the computation. The basepoint set is identi- fied by a basepoint index, and the filter samples are identified by the fractional interval. These two pieces of information must be delivered to the digital interpolating structure by a controller. A number-controlled oscillator (NCO) can provide these parameters via control algorithms presented in the text. Because the NCO is clocked synchronously with the signal samples, the modem output will exhibit timing jitter. This jitter is inconsequential if the data are consumed locally to the modem, because the NCO can provide a symbol clock with the same jitter as the data. If the data must be retransmitted synchronously, the jitter may be intolerable. A jitter-free analog clock can be recovered from the NCO and used to reclock the jittered data prior to retransmission. The fictitious analog interpolating filter should be FIR and should provide good stopband suppression of the periodic images of the sampled input signal. Passband response of this filter is part of the overall filtering of the modem. In consequence, non-flat response in the passband is not charged as distortion, as it would be in a classical interpolator. A designer has wide latitude in distributing overall filter response between the interpolating filter and other filters in the modem. D. Passband Resvonse An ideal interpolator would pass all frequencies from 0 to 1/2T, with flat attenuation and with linear phase. In a modem where signal filtering is to be performed anihow, there is no need for flat transmission in the filter’s passband. The interpolator merely contributes a portion of the filtering that is required for the receiver. Any reasonable passband char- acteristic is permissible, provided that it can be compensated VII. APPENDIX A: ALTERNATIVE CONTROL METHOD M. Moeneclaey has pointed out an alternative control that does not use an NCO. Two successive scheme interpolations are performed for time instants kT, = VI,^: + pk)T, ( k + l)Tz = ( ~ + + i + pk+i)Ts.

GARDNER: INTERPOLATION IN DIGITAL MODEMS-PART I 507 Subtracting these two expressions and rearranging slightly gives the recursion pk - / L k + l . mk+l = mk Ti/Ts (-4.2) By definition, mk+l is an integer. Then, since 0 5 p k + l < 1, (-4.3) whence the increment in sample count from one interpolation to the next is mk+l + pk+l = mk 4- Ti/Ts + pk < m k + 2 Notice that a practical scheme must work with the increment rather than the sample count mk. Any finite-length counter of mk would overflow eventually. To compute the fractional interval PIE, recognize that the fractional part fp[ ] of the increment is zero from which one may conclude The true Ti/T, is not available. Instead, the synchronizer produces a control word V(mk) N TiIT, to be used in the recursions (A.4) and (AS). This control word is the synchronizer’s estimate of the true interpolation period Ti relative to the sampling period T,. The alternative control method may be most useful in systems where the data are consumed at the same location as the data receiver, without reclocking. It is not immediately apparent how a jitter-free, time-continuous clock for retrans- mission could be synthesized easily without the phase v(m) that accumulates in an NCO. ACKNOWLEDGMENT I wish to thank Dr. R. Harris and L. Erup of the European Space Agency for their helpful critiques of the work as it progressed. REFERENCES L. Erup, F. M. Gardner, and R. A. Harris, “Interpolation in digital 11: implementation and performance,” to be published. modems-Part R. E. Crochiere and L. R. Rabiner, Multirate Digital Signal Processing. Englewood Cliffs, NJ: Prentice-Hall, 1983. R. W. Schafer and L. R. Rabiner, “A digital signal processing approach to interpolation,” Proc. IEEE, vol. 61, pp. 692-702, June 1973. R. E. Crochiere, L. R. Rabiner, and R. R. Shively, “A novel imple- mentation of digital phase shifters,” Bell Syst. Tech. J., vol. 54, pp. 1497-1502, Oct. 1975. F. Takahata et al., “A PSK group modem for satellite communication,” IEEE J. Select. Areas Commun., vol. SAC-5, pp. 648-661, May 1987. M. Oerder, G. Ascheid, R. Haeb, and H. Meyr, “An all digital implemen- tation of a receiver for bandwidth efficient communication,” in Signal Processing III (Eusipco 1986), I. T. Young et al. Ed., pp. 1091-1094, Elsevier, 1986. G. Ascheid, M. Oerder, J. Stahl, and H. Meyr, “An all digital receiver architecture for bandwidth efficient transmission at high data rates,” IEEE Trans. Commun., vol. 37, pp. 804-813, Aug. 1989. J. A. C. Bingham, The Theory and Practice of Modem Design. New York: Wiley, 1988. F. M. Gardner, “A BPSWQPSK timing-error detector for sampled receivers,” IEEE Trans. Commun., vol. COM-34, pp. 423-429, May 1986. E. Auer, “An advanced, variable data rate modem for Intelsat IDR/IBS services,” Paper 1-3, Proc. 2nd In?. Workshop Digital Signal Processing Techniques Appl. Space Commun., Turin, Italy, 24-25 Sept. 1990. Floyd M. Gardner (S’49-A’54-SM’58-F’80) re- ceived the B.S.E.E. degree from the Illinois Institute of Technology, Chicago, IL, in 1950, the M.S.E.E. from Stanford University, Stanford, CA, in 1951, and the Ph.D. degree from the University of Illinois, Urbana, IL, 1953. He has been a independent consulting engineer since 1960, active in the fields of communications and electronics. He is a specialist in synchronization and in phase-lock loops, and is the author of the book Phaselock Techniques (New York: Wiley, 2nd edition, 1979). In recent years he has been investigating algorithms for digitally implemented modems. Dr. Gardner is a Registered Professional Engineer in the State of California.

分享到：

赞收藏

资料库

[1993 TC]Interpolation in Digital Modems—Part I： Fundamentals.pdf

相关推荐

课程资源

热门标签

最新资料