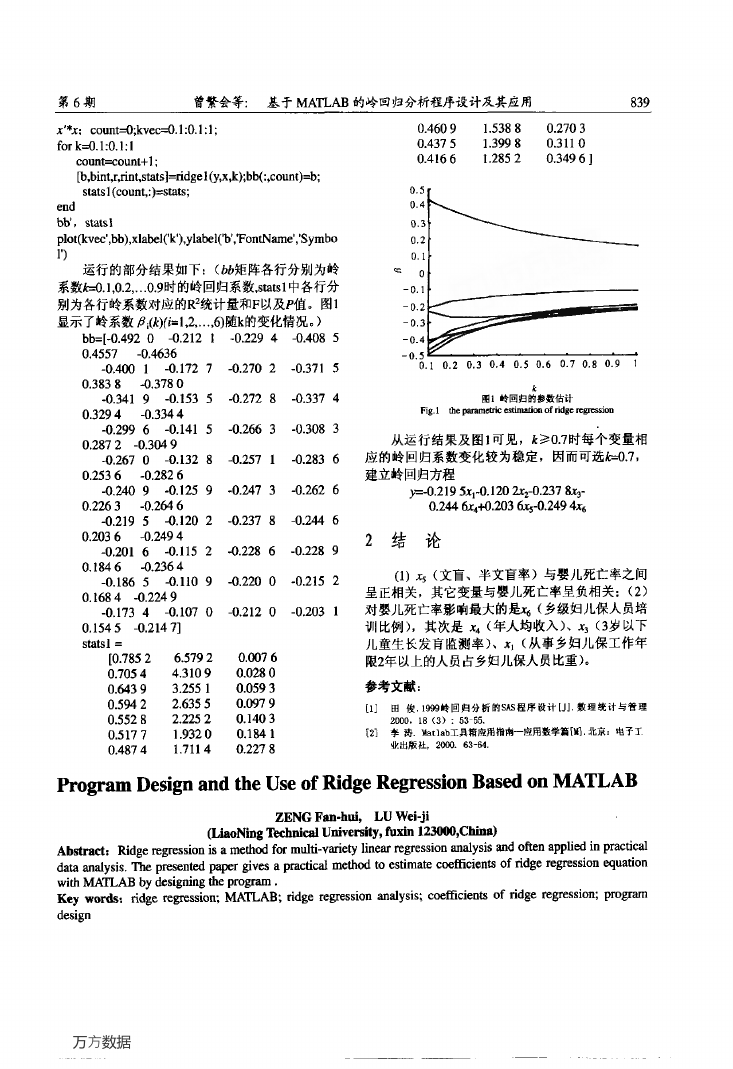
第6期 曾繁会等： 基于MAl几AB的岭回归分析程序设计及其应用 ∥乜；coum=0；kvec=0．1：O．1：l： f研k卸．1：0．1：l coun仁：count+1： [b，bim，Lrinkstatsl=ridgel(y'x，k)；bb(：，count)=b； statsl(count，：)=stats； eⅡd bb’，statsl p10t啡vec’，bb)，xlabel(1¨ylabel(’b’，下bntN啪e‘，’Symbo 1’) 运行的部分结果如下：(蚰矩阵各行分别为岭 系数脚．1，O．2，_o．9时的岭回归系数，s缸csl中各行分 别为各行岭系数对应的R2统计量和F以及P值。图1 显示了岭系数卢．(女)ff-1，2，．，6)随k的变化情况。) bb=『，O．492 O 0．4557 ．04636 _0．212 1 ，O．229 4 —0．408 5 ．0．400 0．383 8 —0．172 7．0．270 2．0-37l 5 1 ．0．3780 ．O．34】9 ’o．153 5 -n272 8 一o．337 4 0_3294 —0．3344 ．0．299 6 —0．14l 5 ．0．266 3 ．0．308 3 0．287 2．0t3049 -o．267 0 一O．132 8 ．0．257 1 _0．283 6 0．253 6 —0．282 6 _o．240 9 ·O．125 9 -O．247 3 ．0．262 6 O．226 3 ．O．2646 ．0．219 5 田．120 2 ．O．237 8 —0．244 6 O．460 9 0．437 5 0．416 6 1．538 8 1．399 8 1．285 2 0．270 3 0-311 O O．3496】 图1．争回归蔷参数估计 me岸咖曲证e血rna6∞0fndgcIqp商如 Fig 1 从运行结果及图1可见，t≥0．7时每个变量相 应的岭回归系数变化较为稳定，因而可选脚．7， 建立岭回归方程 产-0．219缸l一0．120 2廿0．237‰一 O．2“6k+0．203 6岛-0．249瓴 0．203 6 ，0．2494 —0．201 6 ’0．115 2抑．228 6．o．228 9 2结论 0．1846 -0．2364 —0．186 5 m．110 9 ．o．220 O ．0．215 2 0．1684 ．0．2249 ．0．173 4 —0．107 O 一0．212 0 ．0，203 l 0．154 5 —0．214 71 statsl= 【0．785 2 0．7054 0．643 9 0．594 2 0．552 8 0．517 7 0．4874 6．5792 O．007 6 4．3109 3．255l 2．635 5 2．225 2 1．9320 1．711 4 0．0280 0．059 3 0．097 9 0．140 3 0．1841 O．227 8 (1)溉(文盲、半文盲率)与婴儿死亡率之间 呈正相关，其它变量与婴儿死亡率呈负相关；(2) 对婴儿死亡率影响最大的是％(乡级妇儿保人员培 训比例)，其次是五(年人均收入)、而(3岁以下 儿童生长发肓监测率)、而(从事乡妇儿保工作年 限2年以上的人员占乡妇儿保人员比重)。 参考文献： [1] 田惶1999岭回归分析的s^S程序设计[JJ．数理统计与管理 2000．18(3)：53 55． 【2] 车涛Mat】ab工具箱应用指南一应用散学篇【蝴北京：电子工 业出版社，2000．63—64 Pmgmm Design and the Use of硒dge Regressi伽Based伽MATLAB ZENG F衄．hllL LU、^fei_ji (Li舯Ni赡砸咖i咖University，fll对n 1230∞，China) Abstmn：Ridge reg陀ssion is a me山0d fbr mllld—v撕ety 1inear regression锄alysis柚d often appUed in pracdcal data柚aIysis．1k pfesented papcr giVes a p咖廿cal呲thod t0 es廿mate c∞币cien侮of棚ge化gressi叩equ撕on w油MAlLAB by dcsigning me progmm． Key w钾ds：湖ge reg陀踮ion；MAlLAB；ddge reg∞ssion a11alysis；coe佑cients of ridge regression；program desig“ 万方数据 

基于MATLAB的岭回归分析程序设计及其应用 作者： 曾繁会， 吕渭济 作者单位： 刊名： 辽宁工程技术大学工商管理学院, 辽宁工程技术大学学报(自然科学版) 英文刊名： JOURNAL OF LIAONING TECHNICAL UNIVERSITY(NATURAL SCIENCE EDITION) 年，卷(期)： 2001，20(6) 2次 引用次数： 参考文献(2条) 1.田俊 岭回归分析的SAS程序设计[期刊论文]-数理统计与管理 1999(3) 2.李涛 Matlab工具箱应用指南 2000 相似文献(0条) 引证文献(2条) 1.胡晔 MTF与图像要素的相关性研究及外景应用[学位论文]硕士 2006 2.张久军 中国农村居民家庭收入来源和消费支出的多元统计分析[学位论文]硕士 2005 本文链接：http://d.g.wanfangdata.com.cn/Periodical_lngcjsdxxb200106033.aspx 下载时间：2010年3月31日