论文研究-多自由度智能仿生手的联合仿真与控制算法 .pdf-资料库

5 10 15 20 25 30 35 中国科技论文在线 http://www.paper.edu.cn 多自由度智能仿生手的联合仿真与控制算法# 杨志明1，田彦涛1,2，徐卓君1，栗阳1** （1. 吉林大学通信工程学院，长春 130025； 2. 工程仿生教育部重点实验室，长春 130025）摘要：智能假肢是康复医学工程的重要组成成分，在人们生活中起到举足轻重的作用。为了减少实际假肢物理样机设计过程中不必要的物资和时间耗费，提高设计效率，本文采用虚拟技术搭建仿真系统。首先采用 Adams 软件建立 14 个自由度虚拟仿生手模型；然后利用 Matlab/Simulink 模块搭建虚拟仿生手的控制系统。由于仿生手模型的复杂性，本文选择简单易实现的 PD 控制器。最后通过模型和控制系统的接口模块，实现 Matlab 和 Adams 多自由度虚拟仿生手模型的联合仿真。仿真实验表明，虚拟仿生手具有较好的跟踪能力，能够稳定的完成相应手势动作。关键词：智能仿生假手；ADAMS；MATLAB；PD 控制；联合仿真中图分类号：TP15 Multi-degree of Freedom of Intelligent Bionic Hand Co-simulation and Control Algorithm YANG Zhiming1, TIAN Yantao1,2, XU Zhuojun1, YANG LI1 (1. College of Communication Engineering,Jilin University,Changchun 130025; 2. China Key Laboratory of Bionic Engineering,Ministry of Education,Changchun 130025) Abstract: Intelligent prosthesis is an important component of rehabilitation medicine works, and it plays a decisive role in people's lives. In order to reduce the unnecessary material and time-consuming, and improve design efficiency in the actual prosthetics physical prototype design process, this paper uses virtual technology to build a simulation system. First, use the Adams software to create a virtual humanoid robot model with 14 degrees of freedom; second, build a virtual bionic hand’s control system by Matlab / Simulink module. As the complexity of the bionic hand model, this paper choose PD controller, it simpley and easily to achieve.Finally, realize the co-simulation of Matlab and Adams virtual bionic hand model with multi-degree of freedom by the model and control system interface module. Simulation results show that the virtual bionic hand has good tracking ability, and can complete the relevant action steadily. Key words: Intelligent bionic prosthetic hand;ADAMS; MATLAB;PD control;Co-simulation 0 引言 20 世纪中期兴起了一个新的医学领域即康复医学。随着人类社会生活质量的需求以及社会进步，康复医学的地位也越来越重要。智能假肢是康复医学重要内容和组成成分，在人们生活中起到举足轻重的作用。目前为止患者所能购买到的多自由度假手只有英国 Touch Bionics 公司的 i-Limb，官方售价约为 10 万人民币。德国的 Otto Bock 假肢公司近期也推出基金项目：本论文的研究得到了吉林省科技发展重点项目“具有温度、触滑觉临场感的仿生手臂研制与开发”（20090350）和中国高校博士专项科研基金（20100061110029）“具有临场感知智能仿生手臂运动肌电信号建模与模式识别理论方法研究”资助。作者简介：杨志明（1987-），男，硕士研究生，复杂系统建模、优化与控制通信联系人：田彦涛（1958-），男，教授、博士生导师，复杂系统建模与优化控制、分布式智能系统与网络控制、智能机器人系统与控制、模式识别与机器视觉. E-mail: tianyt@jlu.edu.cn - 1 -

40 45 50 55 60 65 中国科技论文在线 http://www.paper.edu.cn 了新型 5 指仿生手 Michelangelo Hand，但其同样面临价格过高的问题，其售价在 20 万元以上，远远超出大多数使用者的承受范围。虽然许多灵巧手样机已经被开发（例如： SmartHand[1]、HIT/DLR[2]和 Vanderbilt[3]等假手），但是，目前残疾人还无法使用这些灵巧手。仍然需要控制算法去开发多自由度的假手样机。目前使用的智能假肢不仅价格昂贵并且灵敏度和准确度并没有达到人们满意的程度，给许多残疾人带来不便[4]。因此，智能假肢的进一步研究对于弥补残疾人残端功能缺陷非常重要。智能假肢实体的开发成本较高且开发周期长，于是为了减少实体设计过程中不必要的物资和时间耗费，虚拟样机[5]技术相继产生。法国M. Renault等人采用虚拟技术对假手及手臂进行仿真研究，实现抓取的动作[6]；哈尔滨工业大学马如奇等人[7]将虚拟技术应用于机械臂的联合仿真，采用PD控制有效的实现了机械臂的跟踪运动。以上国内外采用虚拟技术进行仿真实验多是针对手臂的研究及低自由度的模型的分析，其模型控制起来较为简单，而本文所研究的智能假肢需要对手部多自由度进行控制，实现各式手部动作，控制过程难度较大，目前国内外在这方面的研究也比较少。本文采用虚拟样机 Adams 软件建立虚拟仿生手模型。采用具有强大计算功能的 Matlab 构建虚拟模型的控制系统。目前所采用的控制算法有很多，PD 控制是最经典的算法，该算法结构简单、稳定性好，特别适合非常复杂的控制对象。本文研究的虚拟仿生手模型是非线性复杂模型，因此采用简单易实现的 PD 控制器。通过 ADAMS 与 MATLAB 接口实现的两个软件的联合仿真。实验验证，由于开发智能仿生手臂需要大量的实验，因此开发虚拟假手是很有意义的。目前这方面国内外研究者很少。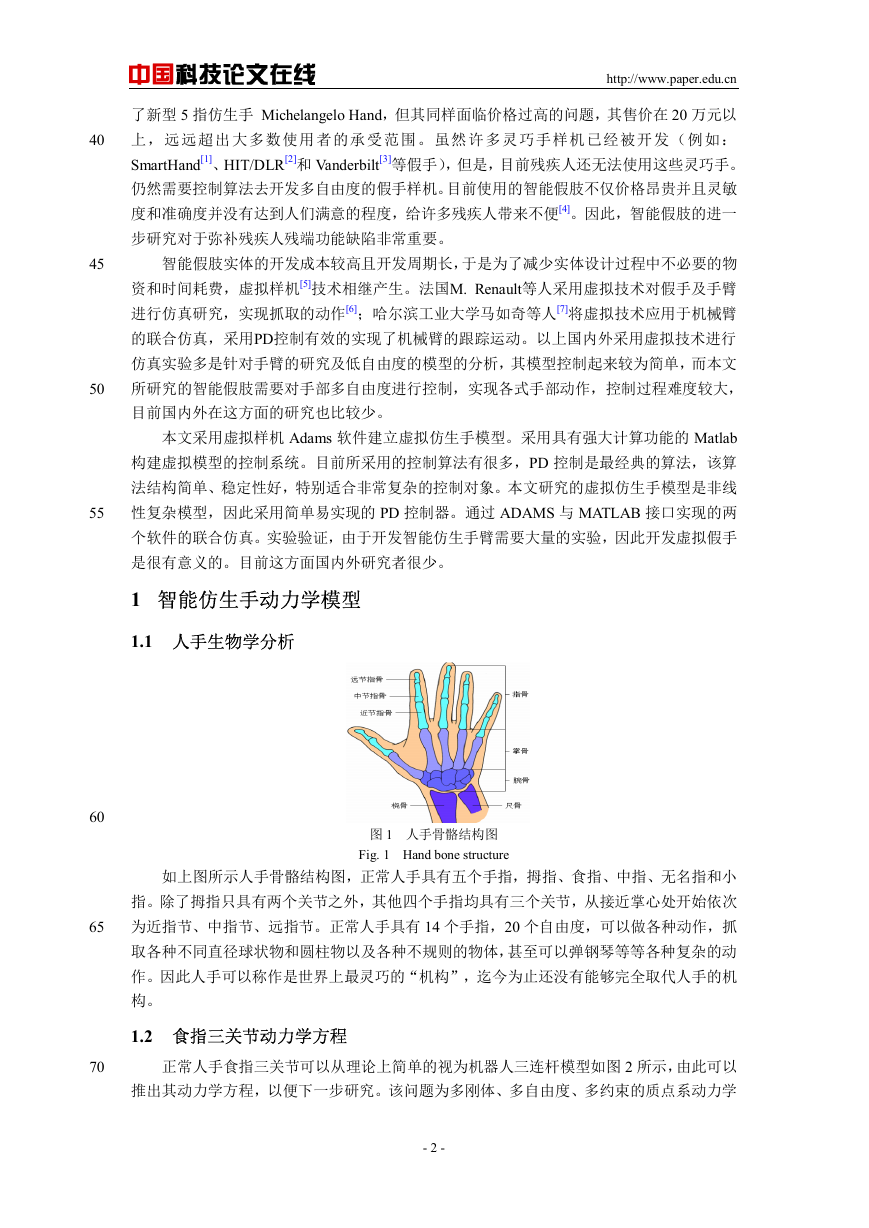 1 智能仿生手动力学模型 1.1 人手生物学分析图 1 人手骨骼结构图 Fig. 1 Hand bone structure 如上图所示人手骨骼结构图，正常人手具有五个手指，拇指、食指、中指、无名指和小指。除了拇指只具有两个关节之外，其他四个手指均具有三个关节，从接近掌心处开始依次为近指节、中指节、远指节。正常人手具有 14 个手指，20 个自由度，可以做各种动作，抓取各种不同直径球状物和圆柱物以及各种不规则的物体，甚至可以弹钢琴等等各种复杂的动作。因此人手可以称作是世界上最灵巧的“机构”，迄今为止还没有能够完全取代人手的机构。 1.2 食指三关节动力学方程 70 正常人手食指三关节可以从理论上简单的视为机器人三连杆模型如图 2 所示，由此可以推出其动力学方程，以便下一步研究。该问题为多刚体、多自由度、多约束的质点系动力学 - 2 -

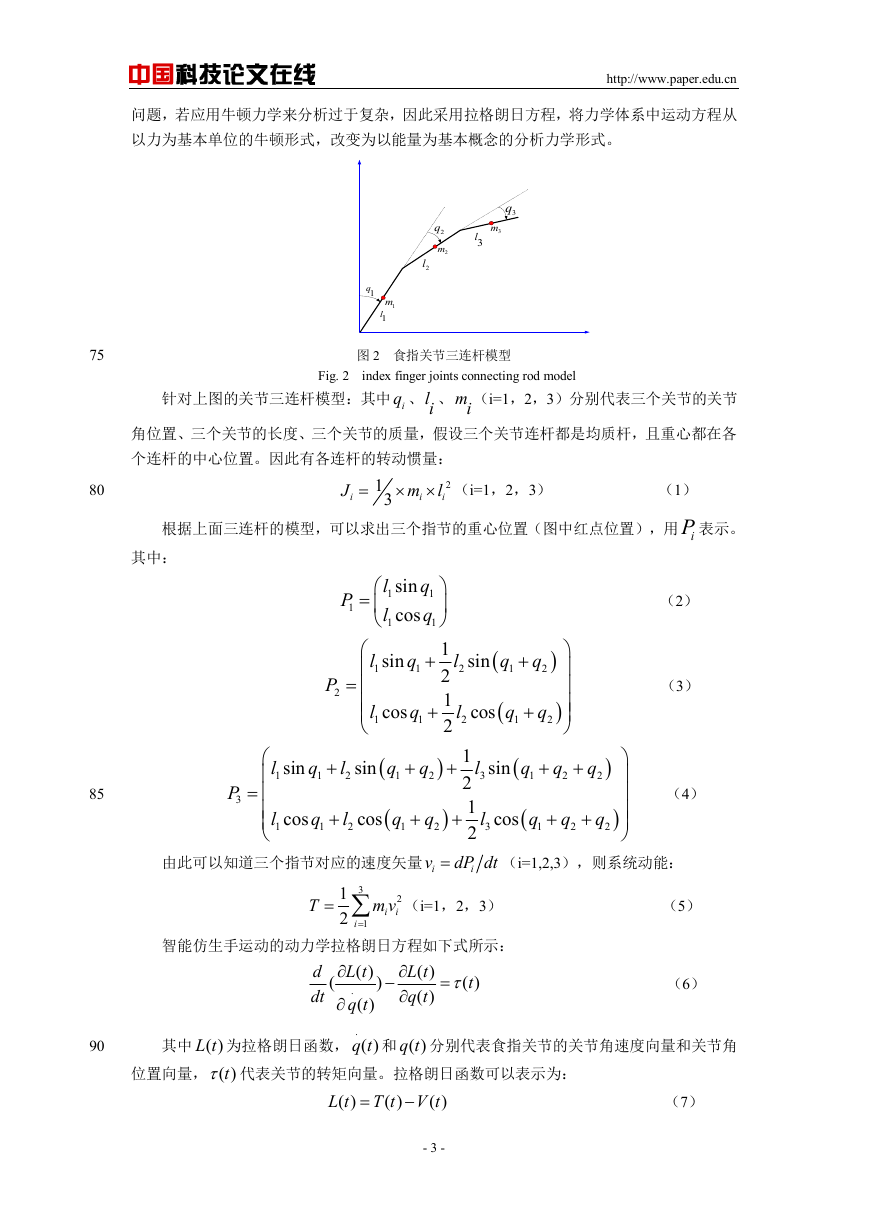
中国科技论文在线 http://www.paper.edu.cn 问题，若应用牛顿力学来分析过于复杂，因此采用拉格朗日方程，将力学体系中运动方程从以力为基本单位的牛顿形式，改变为以能量为基本概念的分析力学形式。 3q 3m 3l 2q 2m 2l 1q 1m 1l 图 2 食指关节三连杆模型 Fig. 2 index finger joints connecting rod model 针对上图的关节三连杆模型：其中 iq 、li 、mi （i=1，2，3）分别代表三个关节的关节角位置、三个关节的长度、三个关节的质量，假设三个关节连杆都是均质杆，且重心都在各个连杆的中心位置。因此有各连杆的转动惯量： 2 × （i=1，2，3）（1） × = 1 J m l i i i 3 根据上面三连杆的模型，可以求出三个指节的重心位置（图中红点位置），用 iP 表示。其中： 75 80 P 1 ⎛ = ⎜ ⎝ l 1 l 1 q sin 1 q cos 1 ⎛ ⎜ = ⎜ ⎜ ⎜ ⎝ l 1 sin q 1 + l 1 cos q 1 + P 2 ⎞ ⎟ ⎠ 1 2 1 2 （2） l 2 sin ( q 1 + q 2 ) l 2 cos ( q 1 + q 2 ) ⎞ ⎟ ⎟ ⎟ ⎟ ⎠ （3） 85 P 3 ⎛ ⎜ = ⎜ ⎜ ⎜ ⎝ l 1 sin q 1 + l 2 sin ( q 1 + q 2 ) + l 3 sin ( q 1 + q 2 + q 2 ) l 1 cos q 1 + l 2 cos ( q 1 + q 2 ) + l 3 cos ( q 1 + q 2 + q 2 ) 1 2 1 2 （4） ⎞ ⎟ ⎟ ⎟ ⎟ ⎠ v 由此可以知道三个指节对应的速度矢量 i = dP dt i （i=1,2,3），则系统动能： T 3 1 = ∑ （i=1，2，3）（5） 2 m v 2 i i i 1 = 智能仿生手运动的动力学拉格朗日方程如下式所示： d dt ( 90 其中 ( )L t 为拉格朗日函数， ∂ ) = − τ t ( ) L t ( ) ∂ q t ( ) ∂ （6） L t ( ) ∂ . q t ( ) . ( )q t 和 ( )q t 分别代表食指关节的关节角速度向量和关节角位置向量， ( )tτ 代表关节的转矩向量。拉格朗日函数可以表示为： L t ( ) = T t V t ( ) ( ) − （7） - 3 -

中国科技论文在线 http://www.paper.edu.cn 其中 ( )T t 和 ( )V t 分别代表在 t 时刻系统的动能和势能。将式（7）代入式（6）中，可以推出食指的三关节动力学方程如下： 95 M q t q t C q t q t ( ( )) ( ) ( ( ), ( )) + . + G q t ( ( )) = tτ ( ) （8）其中 ( ( )) M q t 为惯性矩阵， C q t q t 为哥氏力/离心力矩阵， ( ( )) ( ( ), ( )) G q t 为重力矩 . 阵，因此式（8）可以写成： M q t q t ( ( )) ( ) + . N q t q t ( ( ), ( )) = tτ ( ) (9) . N q t q t ( ( ), ( )) . C q t q t ( ( ), ( )) = + G q t ( ( )) 表示非线性关系。其中 100 由上述可以得出食指三连杆动力学关系，同理可以得出中指、无名指、小指的三连杆动力学关系以及拇指的二连杆动力学关系。 2 智能仿生手的控制系统 2.1 反馈线性化寻找反馈线性化技术将动态方程中的非线性部分用式（9）代替，因此关节 ( )x t 的 105 状态空间表达式可以包含有关节角位置和关节角速度如式（10）所示。 x t ( ) q t ( ) . q t ( ) ⎡ = ⎢ ⎢ ⎣ ⎤ ⎥ ⎥ ⎦ 因此动态模型可以重新被写成：（10） 110 115 120 . d q t ( ) dt = − 1 − M q t N q t q t ( ( ))[ ( ( ), ( )) . τ − t ( )] （11）在布鲁洛夫斯基标准型中我们可以得到一个线性可变状态方程形如： . x t ( ) I 0 0 0 同时给出控制输入矩阵为： ⎡ ⎢ ⎣ = x t ( ) + ⎤ ⎥ ⎦ 0 ⎡ ⎤ ⎢ ⎥ I ⎣ ⎦ u t ( ) （12） u t ( ) = − . 1 − ( ( ))[ tτ ( )] − M q t N q t q t ( ( ), ( ) dq t ，因此跟踪误差 ( )e t 可以被定义为： e t ( ) q t ( ) − q t ( ) d （13）假设假手的期望轨迹为 ( ) = （14） dq t 为期望关节角矩阵， ( )q t 为实际关节角矩阵。同时对式（14），两次其中， ( ) 求导数得到： = 将式（10）代入式（16）中得到： = ⋅ e t ( ) .. e t ( ) . q t ( ) d .. q t ( ) d . q t ( ) .. q t ( ) − − （15）（16） .. e t ( ) = .. q t M q t N q t q t d ( ( ), ( )) ( ( ))[ ( ) + − 1 . tτ − ( )] （17）其中，控制输入函数可以被定义为： - 4 -

中国科技论文在线 tτ − 这通常被称为反馈线性化控制律，也可以反向表达它为： .. q t M q t N q t q t d ( ( ), ( )) ( ( ))[ u t ( ) ( ) = + − 1 . ( )] http://www.paper.edu.cn （18） τ = t M q t ( ) ( ( ))[ .. q t ( ) d − u t ( )] + . N q t q t ( ( ), ( )) （19） 125 通过式（16）和式（18）的关系，定义状态向量 x t ( ) = e t [ ( ) , . e t ( ) ] , , ，跟踪误差可以写为： . x t ( ) = ⎡ ⎢ ⎣ 这是一个线性系统形如 I 0 0 0 . x t ( ) x t ( ) + ⎤ ⎥ ⎦ 0 ⎡ ⎤ ⎢ ⎥ I ⎣ ⎦ u t ( ) （20） = Ax t ( ) + Bu t ( ) 。 2.2 PD 控制器的设计图 3 为 PD 控制器的结构框图。 130 ,q q& N(q,q)& + τ + qd&& e& e qd& + − qd + − + + + q& q 图 3 PD 控制器的结构框图 Fig. 3 the structure diagram of the PD controller 控制信号 ( )u t 为 135 u t ( ) = − K e t K e t ( ) ( ) − （21） p . d 其中 pK 和 dK 分别为控制器中的比例和微分系数。然后，闭环误差动力学和状态空间形式可以写成： . + .. e t K e t ( ) ( ) e t ( ) ⎤ d ⎥ . dt e t ⎥ ( ) ⎦ 0 − ⎡ ⎢ ⎢ ⎣ ⎡ ⎢ ⎣ K = p d − + K e t ( ) = （22） e t ( ) ⎡ I ⎢ . K e t ⎢ ( ) ⎣ （23） 0 ⎡ ⎤ ⎢ ⎥ I ⎣ ⎦ 0 ⎤ ⎥ ⎥ ⎦ p ⎤ ⎥ ⎦ u t ( ) + d 140 和 τ = t M q t ( ) ( ( ))( .. q t K e t K e t d ( ) ( ) + + ( )) d p . . N q t q t ( ( ), ( )) + （24） 3 ADAMS 和 MATLAB 软件联合仿真 3.1 智能仿生手的虚拟样机开发本文采用在 ADAMS/View 界面中选择不同的几何实体，如立方体、球、圆柱等， - 5 -

中国科技论文在线 http://www.paper.edu.cn 145 150 通过各种运动副的连接和组合并结合实际手的形状、长度以及质量建立智能仿生手的三维虚拟模型。建立的虚拟模型中，和实际人手一样，拇指具有两个关节，添加两个转动副，为了研究方便，我们将指根部用固定副固定，因此拇指具有两个自由度；同理，针对其他四个手指，均具有三个关节，添加三个转动副，指根部添加固定副固定，因此其他四个手指均具有三个自由度。综上，在 ADAMS 中设计的虚拟假手具有五个手指，共计 14 个自由度。对于每个自由度设置各自的变量，同时设置每个自由度对应的控制转矩变量作为驱动仿生手关节运动的转矩指令。表 1 为 ADAMS 中虚拟假手采用的实际手的质量和长度参数。表 1 虚拟仿生手参数 Tab. 1 virtual bionic hand parameters 名称质量(Kg) 长度(m) 拇指食指中指无名指小指指根指尖指根指中指尖指根指中指尖指根指中指尖指根指中指尖 155 5.544E-002 5.544E-002 6.949E-002 6.4229E-002 6.247E-002 7.124E-002 6.598E-002 6.5983E-002 7.124E-002 6.422E-002 6.247E-002 6.071E-002 6.422E-002 6.071E-002 0.02 0.02 0.028 0.025 0.024 0.029 0.026 0.026 0.029 0.025 0.024 0.023 0.025 0.023 为了能够更精确的完成各种手势动作，本文设计的假手模型拇指和正常人手的位置不太一样，但是不会影响假手的运动效果，因此设计的假手模型基本接近实际人手。 3.2 联合仿真实验将 ADAMS 软件中建立的虚拟假手模型和 MATLAB 软件中建立的控制系统通过图 4 的 160 形式结合起来，形成一个闭环系统[8]。 ADAMS的输入 ADAMS的输出 A D A M S \ C o n t r o l s 接口插件 MATLAB的输出 MATLAB的输入 A D A M S \ C o n t r o l s 图 4 ADAMS/ MATLAB 的输入输出 Fig.4 ADAMS/MATLAB input and output 从菜单 Tools 选择 Plugin Manager 命令,该对话框提供了几个模块供 ADAMS/ View 加载。选取 Controls 模块，Controls 接口是实现 ADAMS 和 MATLAB 联合仿真的重要部分[9]， 165 - 6 -

中国科技论文在线 http://www.paper.edu.cn 在 Controls/Plant Export 中设置控制系统输入输出变量，如图 5 所示。图 5 联合仿真接口 Fig. 5 co-simulation interface 170 175 在Adams／control模块中，将转矩变量定义为输入变量，用于存放Matlab中控制系统输出的转矩指令；将位置变量定义为输出变量，用于控制系统中的位置。变量定义完成后， Adams／control模块将会生成三个文件，这些文件将用于Adams与Matlab之间进行数据传递。在Matlab中调用Adams／control模块，显示已经定义的联合仿真系统所需要的14个变量，并对这些变量进行确认。然后在Matlab中输人命令：adams_sys，Matlab将会产生假手机械子系统模块，如图6所示。（a）联合仿真系统中的机械子系统（b）机械子系统结构图 6 联合仿真系统中的机械子系统及其结构 Fig. 6 mechanical subsystem of co-simulation and its structure 从图中可以看出，机械子系统 ADAMS Plant 有 14 个转矩变量作为输入，14 个位置变量作为输出。在 ADAMS plant 中设置参数[10]如表 2 所示；在 Simulink 窗口里设置仿真时间为 13 秒，点击开始按钮开始仿真，仿真结果如图所示。 - 7 - 180 185 190

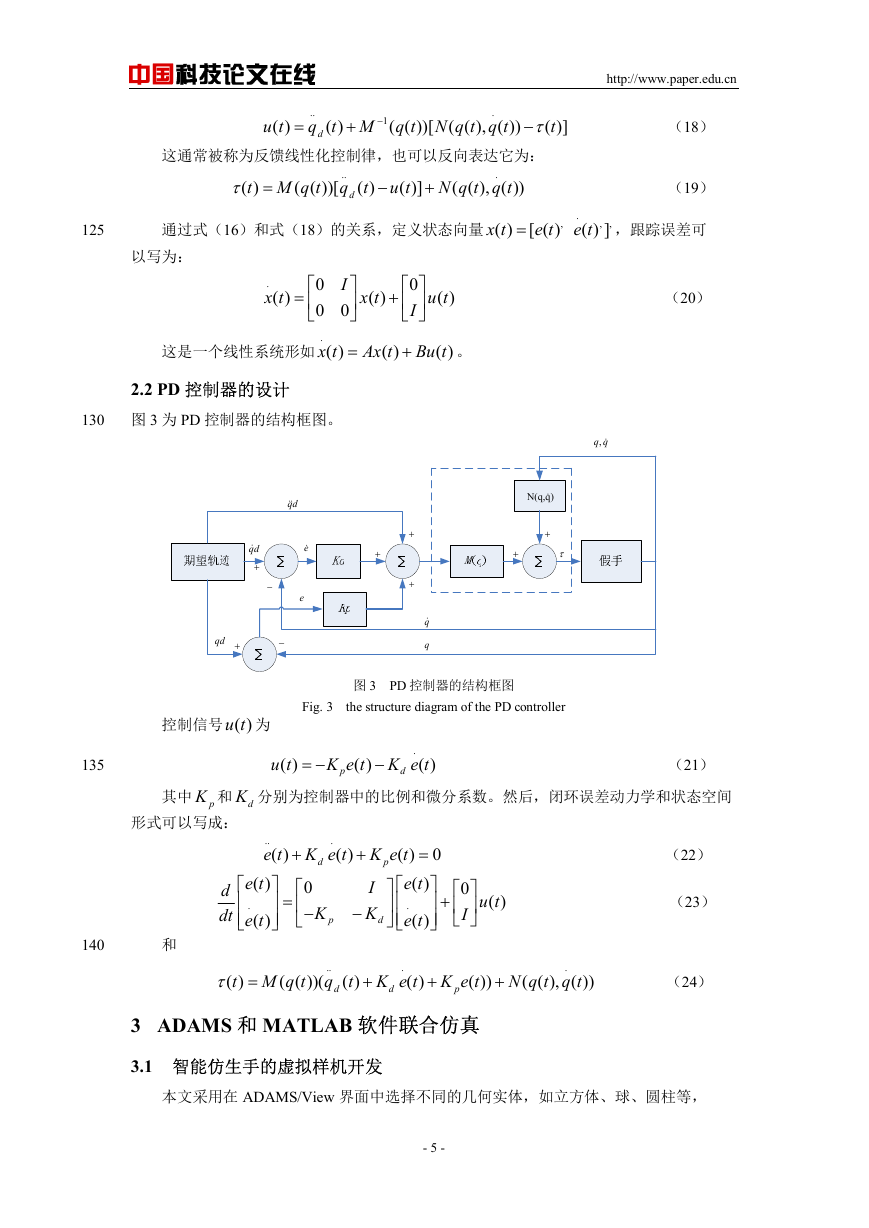
中国科技论文在线 http://www.paper.edu.cn 参数 Interprocess Option Communication Interval Animation mode 表 2 ADAMS/plant 中的参数设置 Tab. 2 parameter settings in the ADAMS/plant 设置说明 PIPE（DDE）表示 ADAMS 和 MATLAB 安装在同一台机器上 0.005 batch 表示 ADAMS 和 MATLAB 每隔 0.005 秒进行一次数据交换采用批处理形式 (a) 关节角度 (b) 转动力矩 (c) 误差曲线 (d)ADAMS 中控制效果图 7 关节角度，转动力矩，误差曲线和 ADAMS 中控效果图 Fig. 7 joint angles ,torque ,error curve and control effect inADAMS 从图中可以看出，调整控制器参数使控制对象达到最佳效果，图 7（a）曲线表明三个关节很快达到目标位置角度，即快速达到稳定状态，且不存在超调现象，有效的完成了目标动作；图 7(b)表示转动力矩曲线；图 7(c)表明三个关节的误差曲线，很明显误差很快趋近于零；图 7(d)表示食指在 ADAMS 中的控制效果图。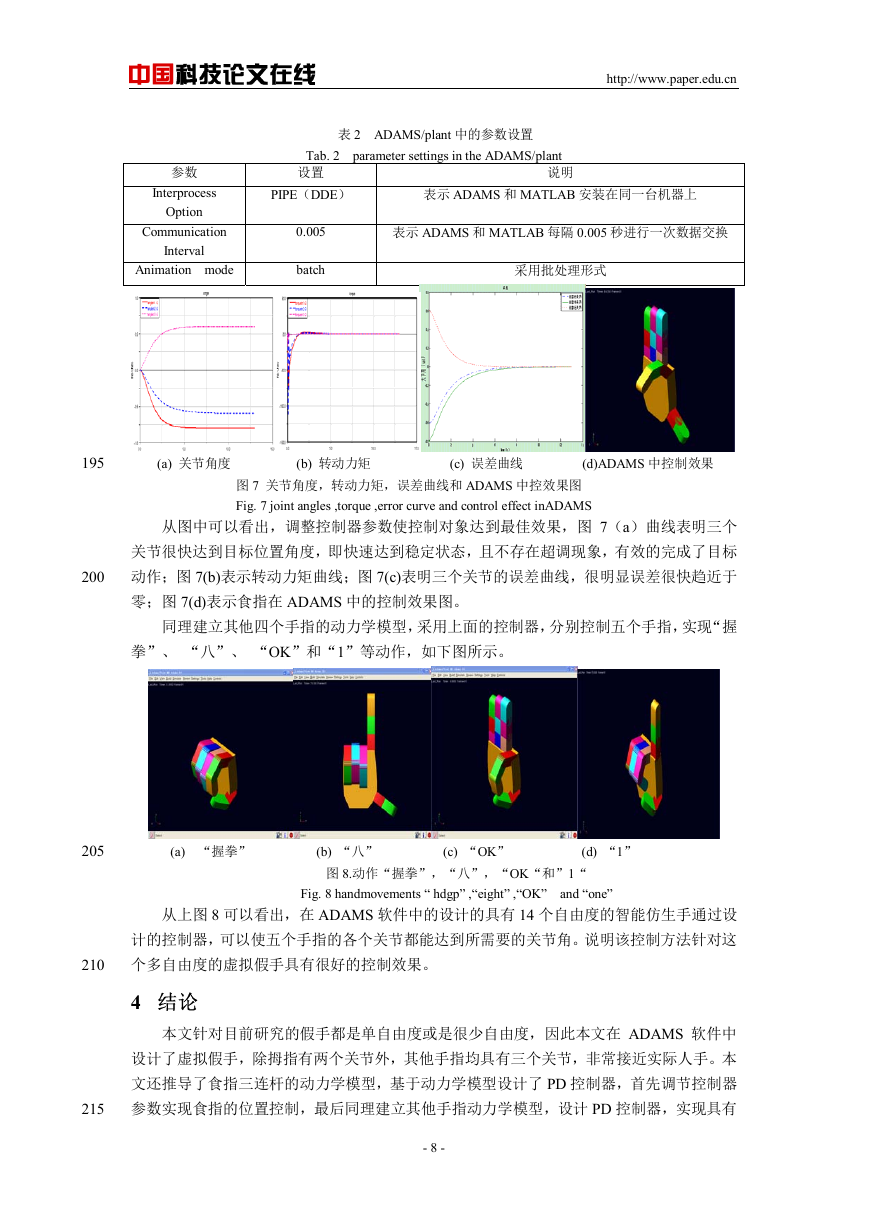同理建立其他四个手指的动力学模型，采用上面的控制器，分别控制五个手指，实现“握拳”、 “八”、 “OK”和“1”等动作，如下图所示。 (a) “握拳” (b) “八” (c) “OK” (d) “1” 图 8.动作“握拳”，“八”，“OK“和”1“ Fig. 8 handmovements “ hdgp” ,“eight” ,“OK” and “one” 从上图 8 可以看出，在 ADAMS 软件中的设计的具有 14 个自由度的智能仿生手通过设计的控制器，可以使五个手指的各个关节都能达到所需要的关节角。说明该控制方法针对这个多自由度的虚拟假手具有很好的控制效果。 4 结论本文针对目前研究的假手都是单自由度或是很少自由度，因此本文在 ADAMS 软件中设计了虚拟假手，除拇指有两个关节外，其他手指均具有三个关节，非常接近实际人手。本文还推导了食指三连杆的动力学模型，基于动力学模型设计了 PD 控制器，首先调节控制器参数实现食指的位置控制，最后同理建立其他手指动力学模型，设计 PD 控制器，实现具有 - 8 - 195 200 205 210 215

资料库

论文研究-多自由度智能仿生手的联合仿真与控制算法 .pdf

相关推荐

开发技术

热门标签

最新资料