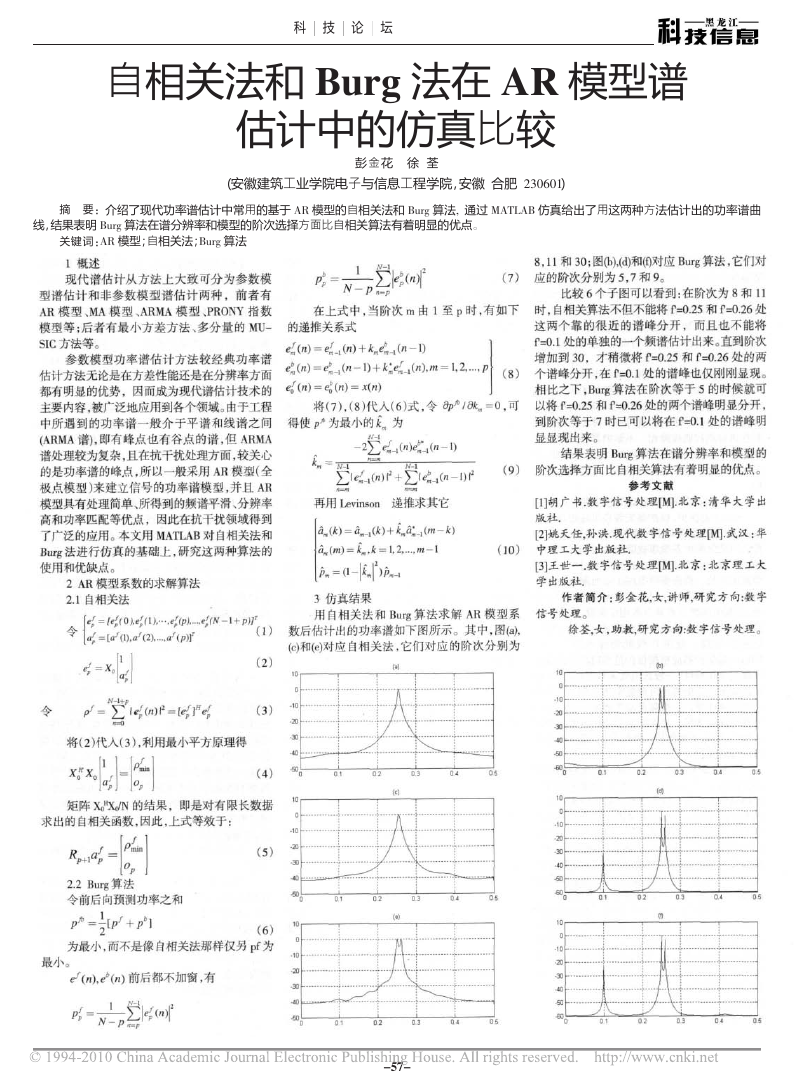
n 30 Burg 和 线，结果表明 ./01 算法在谱分辨率和模型的阶次选择方面比自相关算法有着明显的优点。 1 现代谱估计从方法上大致可分为参数模 型谱估计和非参数模型谱估计两种，前者有 指数 模型 模型 模型 AR 模型等；后者有最小方差方法 、ARMA 、MA 。 SIC 方法等 参数模型功率谱估计方法较经典功率谱 估计方法无论是在方差性能还是在分辨率方面 都有明显的优势，因而成为现代谱估计技术的 由于工程 主要内容，被广泛地应用到各个领域 。 中所遇到的功率谱一般介于平谱和线谱之间 MU- (f) 和 对应 9。 f'=0.25 比较 6
/ k 和 8 f'=0.26 由 至 1 p m ( ) e n N p   e e （ ） 8 （ ） 7  1, 2,...,  p    ( k e 时，有如下 ，才稍微将 ( ) e n ( ) e n 算法，它们对 的递推关系式 彭金花 徐 荃 在上式中，当阶次 和 (b),(d) ， 7 5 、PRONY 多分量的 、 科 技 论 坛 个子图可以看到：在阶次为 处的单独的一个频谱估计出来 和 ， 8 11 应的阶次分别为 ；图 30 关键词：,- 模型；自相关法；./01 算法 法在 模型谱 （安徽建筑工业学院电子与信息工程学院，安徽 合肥 !"#$#%） 自相关法和 1)  ( ), n m ( ) k e n  1) ( n   ( ) ( ) x n e n   ），（ 将（ ）代入（ ）式，令 6 8 7 得使 为最小的 为 摘 要： 介绍了现代功率谱估计中常用的基于 ,- 模型的自相关法和 ./01 算法* 通过 (,23,. 仿真给出了用这两种方法估计出的功率谱曲 Burg AR 估计中的仿真比较 11 时，自相关算法不但不能将 处 这两个靠的很近的谱峰分开，而且也不能将 直到阶次 。 处的两 f'=0.25 f'=0.26 处的谱峰也仅刚刚显现 。 的时候就可 处的两个谱峰明显分开， 处的谱峰明
p


1



e n  



( )





p


e







X
k






2



 


X








a k








e

1

e 
|
e n



X X 
1 


R a





p 
1


 [1]胡广书&数字信号处理’()&北京：清华大学出 版社& ’!)姚天任*孙洪&现代数字信号处理’()&武汉：华 中理工大学出版社& ’")王世一&数字信号处理’()&北京：北京理工大 学出版社& f'=0.1 增加到 个谱峰分开，在 相比之下， 以将 f'=0.25 到阶次等于 显显现出来 7 。 结果表明 

     o     的结果，即是对有限长数据 p 为最小，而不是像自相关法那样仅另 (a), 对应自相关法，它们对应的阶次分别为  a m X (      仿真结果 作者简介：彭金花*女*讲师*研究方向+数字 徐荃*女，助教*研究方向+数字信号处理。 ）代入（ 将（ ），利用最小平方原理得 3 2 阶次选择方面比自相关算法有着明显的优点 2.2 Burg 令前后向预测功率之和 数后估计出的功率谱如下图所示 算法在谱分辨率和模型的 f'=0.1 算法在阶次等于 3 用自相关法和 f'=0.26 时已可以将在 模型系数的求解算法 前后都不加窗，有    o   算法 信号处理。 AR 其中，图 递推求其它 X
     （ ） 6 为 2 AR 2.1
      a 算法求解 自相关法 参考文献 [e ( 0 ),e ( ), 1 ,e (p), ... ,e (N （ ） 1 （ ） 3 （ ） 5 (2),..., a ( p )] （ ） 4 ） （ 2 ） （ 9 模型系 k ( )  k a X X ( )  a X )  X k k , Burg 和 ( ) |
[ e ] e  1, 2,..., m  1   N p Levinson X0 HX0/N （ ） 10 n (
1) | (c) (e) ，可 0 n ( ) |  ( ) n e ( n
1)
[ p m k  ( )  e | (1 X k p X )     a   1 p)] [ a (1), a 谱 ，即有峰点也有谷点的谱，但 ) (ARMA ARMA 谱处理较为复杂，且在抗干扰处理方面，较关心 模型（全 的是功率谱的峰点，所以一般采用 极点模型）来建立信号的功率谱模型，并且 AR 模型具有处理简单 分辨率 、 高和功率匹配等优点，因此在抗干扰领域得到 了广泛的应用 对自相关法和 法进行仿真的基础上，研究这两种算法的 所得到的频谱平滑 、 MATLAB 本文用 AR 。 求出的自相关函数，因此，上式等效于： Burg 使用和优缺点 。 p X k  再用 。 ( ) e n e n ( ), 和 5 f'=0.1
    a 1 2          p ] Burg 。 p X 和  e | 令 令
Burg 。 最小 pf 概述 矩阵 ( ) e n －57－