第 ２８ 卷第 ７ 期 ２０１１ 年 ７ 月　 计 算 机 应 用 研 究 Ａｐｐｌｉｃａｔｉｏｎ Ｒｅｓｅａｒｃｈ ｏｆ Ｃｏｍｐｕｔｅｒｓ Ｖｏｌ．２８ Ｎｏ．７ Ｊｕｌ．２０１１ 倡 基 于 空 间 引 力 作 用 的 复 杂 网 络 演 化 模 型 １，２， 韩景倜 １ 李周平 （１．上海财经大学 信息管理与工程学院， 上海 ２００４３３； ２．上海理工大学 管理学院， 上海 ２０００９３） 摘　要： 为了研究空间距离、边权演化、节点规模等因素在复杂网络演化过程中的共同作用，借助空间引力模 型，采用基尼系数的统计方法，综合分析这三种因素对网络拓扑结构异质性的影响作用。 数值仿真研究表明，空 间距离、边权演化作用并不改变网络结构的无标度性；演化过程中节点规模的分布同时受空间距离、边权演化因 素影响；网络连边距离分布符合幂律函数，其中幂指数与空间距离因素相关，而与边权演化因素无明显关系。 关键词： 复杂网络； 空间距离； 边权演化； 节点规模； 引力模型 中图分类号： ＴＰ３０１畅６；ＴＰ３９３　　　文献标志码： Ａ　　　文章编号： １００１唱３６９５（２０１１）０７唱２６２５唱０３ ｄｏｉ：１０．３９６９／ｊ．ｉｓｓｎ．１００１唱３６９５．２０１１．０７．０６３ Ｍｏｄｅｌｉｎｇ ｅｖｏｌｕｔｉｏｎ ｏｆ ｃｏｍｐｌｅｘ ｎｅｔｗｏｒｋｓ ｂａｓｅｄ ｏｎ ｓｐａｔｉａｌ ｇｒａｖｉｔａｔｉｏｎ ＬＩ Ｚｈｏｕ唱ｐｉｎｇ１，２， ＨＡＮ Ｊｉｎｇ唱ｔｉ１ （１．School of Information Management ＆ Engineering， Shanghai University of Finance ＆ Economics， Shanghai ２００４３３，China； ２．Business School， University of Shanghai for Science ＆ Technology， Shanghai ２０００９３， China） Abstract： Ｂｙ ｕｓｉｎｇ ｓｐａｔｉａｌ ｉｎｔｅｒａｃｔｉｏｎｓ ｍｏｄｅｌ ａｎｄ Ｇｉｎｉ ｃｏｅｆｆｉｃｉｅｎｔ， ｔｈｉｓ ｐａｐｅｒ ａｎａｌｙｓｅｄ ｔｈｅ ｇｅｏｇｒａｐｈｉｃａｌ ａｔｔｒｉｂｕｔｅｓ，ｗｅｉｇｈｔ ｄｙ唱 ｎａｍｉｃａｌ ｅｖｏｌｕｔｉｏｎ ａｎｄ ｖｅｒｔｉｃｅｓ ｓｃａｌｅ ｆｉｔｎｅｓｓｅｓ ｔｈａｔ ｉｎｆｌｕｅｎｃｅｄ ｔｈｅ ｐｒｏｃｅｄｕｒｅ ｏｆ ｃｏｍｐｌｅｘ ｎｅｔｗｏｒｋｓ ｅｖｏｌｕｔｉｏｎ．Ｔｈｅ ｎｕｍｅｒｉｃａｌ ｓｔｕｄｙ ｉｎｄｉｃａｔｅｓ ｔｈａｔ ｇｅｏｇｒａｐｈｉｃａｌ ａｔｔｒｉｂｕｔｅｓ ａｎｄ ｗｅｉｇｈｔ ｄｙｎａｍｉｃａｌ ｅｖｏｌｕｔｉｏｎ ａｆｆｅｃｔ ｖｅｒｔｉｃｅｓ ｓｃａｌｅ ｆｉｔｎｅｓｓｅｓ ｄｉｓｔｒｉｂｕｔｉｏｎ， ｂｕｔ ｔｈｅ ｔｗｏ ｆａｃ唱 ｔｏｒｓ ｄｏ ｎｏｔ ｃｈａｎｇｅ ｔｈｅ ｃｏｎｎｅｃｔｉｖｉｔｙ ｐｏｗｅｒ 唱ｌａｗ ｂｅｈａｖｉｏｒ．Ａｎｄ ｔｈｅ ｌｉｎｋ ｌｅｎｇｔｈ ｄｉｓｔｒｉｂｕｔｉｏｎ ｆｏｌｌｏｗｓ ａ ｐｏｗｅｒ ｌａｗ， ｂｕｔ ｔｈｅ ｐｏｗｅｒ ｅｘｐｏｎｅｎｔ ｉｓ ｄｅｐｅｎｄｅｎｔ ｏｎ ｔｈｅ ｃｏｅｆｆｉｃｉｅｎｔ ｏｆ ｓｐａｔｉａｌ ｇｒａｖｉｔａｔｉｏｎ， ｎｏｔ ｏｎ ｔｈｅ ｗｅｉｇｈｔ ｄｙｎａｍｉｃａｌ ｅｖｏｌｕｔｉｏｎ ｆａｃｔｏｒ． Key words： ｃｏｍｐｌｅｘ ｎｅｔｗｏｒｋｓ； ｇｅｏｇｒａｐｈｉｃａｌ ａｔｔｒｉｂｕｔｅｓ； ｗｅｉｇｈｔ ｄｙｎａｍｉｃａｌ ｅｖｏｌｕｔｉｏｎ； ｖｅｒｔｉｃｅｓ ｓｃａｌｅ ｆｉｔｎｅｓｓｅｓ； ｇｒａｖｉｔｙ ｍｏｄｅｌ ［１］ ［２４］ 提出 但是在真实网络中，作为反映网络演化特性的各种影响因 　　作为复杂性科学的新分支，经过十余年的发展，国内外学 素，在网络演化过程中应该是同时存在，共同影响网络的演化 者对复杂网络的研究逐步深入，关于复杂网络演化过程的研究 过程。 独立地研究某一种因素对复杂网络演化的作用，可能丢 取得了丰硕成果。 １９９９ 年，Ａｌｂｅｒｔ 等人 在 ＢＡ 网络演化模型 失真实网络中大量有意义的拓扑特性。 出于以上考虑，本文将 中，通过引入增长和择优连接这两个重要的演化机制，解释了 构造基于空间引力作用下的加权复杂网络演化模型，综合分析 Ｉｎｔｅｒｎｅｔ 网络结构的无标度性质。 然而Ｉｎｔｅｒｎｅｔ、运输、人际关系 空间距离、边权演化、节点规模三种因素在复杂网络演化过程 等一系列真实网络，常常受到空间、边权演化、节点规模等影 中所扮演的不同角色，并利用基尼系数的统计方法衡量各种因 响。 首先，大部分真实网络均处于特定地理空间中，空间距离 素对网络结构异质性的影响作用。 对于节点之间联系产生着重要影响。 因此，Ｂａｒｒａｔ 等人 了基于空间距离约束的复杂网络演化模型，他们都指出了该模 1　网络演化模型 型中节点之间的物理距离对于节点间连边的阻抗作用，并从不 同角度分析了空间距离因素对于网络特征的影响。 其次真实 经济地理引力理论认为，各空间节点的联系存在着类似万 网络中各节点的联系有强弱之分，并且这种联系应该是动态变 有引力的规律。 在如 Ｉｎｔｅｒｎｅｔ、人际关系等复杂网络中，各节点 化的。 Ｂａｒｒａｔ 等人 间的具体联系难以得到准确的统计数据，但是，可以认为网络 化模型，他们认为只有在网络连边中引入权重，才能真正反映 各节点也存在着类似万有引力规律的联系，各节点间联系遵循 真实世界网络的本质，并进一步指出复杂网络中的边权也不是 ij。 其中，Tij 为两节点间的引 固定不变的，而应随着网络演化进行动态调整。 另外，在网络 力联系强度，在复杂网络中 θ 属性应反映节点自身的发展规 演化过程中，节点自身的发展也将对各节点之间的联系产生重 模，L 表示两节点间的空间距离，系数 b 则反映空间距离对节 要作用。 Ｇａｒｌａｓｃｈｅｌｌｉ 等人 点间引力影响作用的强弱。 考虑 Ｉｎｔｅｒｎｅｔ 等复杂网络中，两个 化对复杂网络演化的影响。 他认为在网络中节点应具有反映 节点间新的联系建立必然会引起相邻节点间联系的变化，因 自身规模的某种特有属性，如在 Ｉｎｔｅｒｎｅｔ 中，各路由节点的网络 此，本文在 Ｂａｒｒａｔ 等人 所提出的经典边权演化模型基础上， 流量正是反映节点规模的特有属性。 构造边权动态演化机制，并引入边权演化系数 λ，用于反映新 　　收稿日期： ２０１０唱１２唱１２； 修回日期： ２０１１唱０１唱２０　　基金项目： 国家自然科学基金资助项目（６１０７４１３４）；上海财经大学“２１１ 工程” 三期重点 学科建设项目；上海财经大学研究生科研创新基金资助项目 　　作者简介：李周平（１９８１唱），男，四川广元人，博士研究生，主要研究方向为复杂网路、应急管理（ｌｉｚｈｏｕｐｉｎｇ＠１２６．ｃｏｍ）；韩景倜（１９５９唱），男，陕 西西安人，教授，主要研究方向为复杂系统、应急管理． 提出了边权动态演化的加权复杂网络演 揭示了网络节点的自身规模变 ［９］ Tij ＝θiθjLb 经典的空间引力模型 ［５，６］ ［７，８］ ［６］ 

·６２６２· 节点的引入对于相邻节点的影响程度。 综上所述，本文模型将建立在网络增长制、边权演化、节点 成长三种演化机制基础之上。 其中，网络增长机制主导网络拓 扑结构的增长，以及新节点与老节点间基于空间引力作用的择 优连接；边权演化机制定义了新边引入对于相邻边权重的影 响；节点成长机制体现了在网络演化过程中节点自身规模属性 的增长。 １）网络增长机制　初始状态，该网络由 N０ ＝３ 个种子节 点构成，在边长为１ 的单位正方形区域内，为各节点随机分配 （x，y）二维空间坐标，并分配初始规模属性值 θ０ ＝１，各节点之 间相互连接，初始边权 W０ ＝１。 在每个时间步，系统引入一个 新节点 n，该新节点在网络已存在的 m 个节点中，选择 １ 个节 点进行择优连接，择优连接的概率为 力强度值为 　　j∈V（i） Πn→i ＝ Tin∑jTjn （１） 其中：Πn→i为节点 n 与节点 i 连接的概率值；Tin 为节点 i 对节 点 n 的引力强度；∑jTjn为系统已存节点对节点 n 的引力强度 之和；V（i）为与节点 i 具有连边的节点集合。 根据空间引力模型，复杂网络中，两节点间相互作用的引 （２） 可以发现，本模型中新加入的节点将以较大概率与对它具 有较强引力的老节点产生联系，而节点间的引力又与各节点的 自身发展规模与节点间的距离密切相关。 因此，通过引力作用 驱动的增长机制，在 ＢＡ 模型 引入了空间距离与节点规模因素，这更能反映真实网络的演化 作用。 ２）边权演化机制　出于简化模型考虑，如图 １ 所示，引入 每条新边的权重 Wni ＝W０ ＝１。 但新边权重的引入，会造成相 邻边权重变化。 根据 Ｂａｒｒａｔ 等人 型，由于节点 i 引入新边，导致节点 i 原邻边的权重增加 ΔWij， 而节点 i 邻边权重增加的总和∑jΔWij 与新加边的权值线性相 关为 λW０，如式（３）（４）所示。 （３） （４） ∑jΔWij按照节点 i 各邻边的原有权值按比例分配给各邻 边 ΔWij值，如式（５）所示。 其中，λ为边权演化系数，Si 为节点 i 强度，即与节点 i 相连边的权值之和。 Wij ＝Wij ＋ΔWij　　j∈V（i） ∑jΔWij ＝λW０　　j∈V（i） 纯粹依靠度偏好增长的基础上 所提出的经典边权演化模 Tij ＝θiθjLb ij ［１］ ［６］ ΔWij ＝λW０ Wij Si 　　j∈V（i） （５） 网络边权演化机制促使网络中各边的边权并不是固定不 变的，而是随着网络规模的不断增大而动态变化。 λ系数模拟 了真实网络中新节点的引入对已有节点的拉动作用，λ系数越 大说明新节点的引入对于局部网络的拉动作用越大。 ３）节点成长机制　在真实网络中，如 Ｉｎｔｅｒｎｅｔ，各节点的数 据传输规模将随着网络的演化而增长。 因此，模型中引入节点 规模属性 θ 来模拟真实网络中的节点成长。 在网络增长以及 边权演化的过程中，节点的规模属性 θ 也随之动态变化，θ 的 变化机制如式（６）所示。 （６） θi ＝θ０ ＋Si 计 算 机 应 用 研 究 　 第 ２８ 卷 其中，θ０ 为节点的初始规模值，Si 为节点 i 的强度值。 由于节点 强度 Si 在网络规模增长与网络边权演化机制的作用下动态变 化，因此网络节点的规模属性 θ 也将动态变化。 如图１ 所示，新 节点 n 的引入，对于与其产生连边的节点 i 以及节点 i 的相邻节 点的规模属性θ 都会产生影响。 而网络节点规模属性 θ 的动态 变化又将通过式（２）进一步影响复杂网络的演化过程。 P（k）∝k －γ 2　仿真分析 现实世界中存在的大部分复杂网络，各节点度值与强度分 布存在强烈的不均匀性，这一类复杂网络称为无标度网络。 经 典 ＢＡ 无标度网络模型揭示了节点度值分布满足幂律函数 特性： 其中：P（k）是节点度值为 k 的概率，γ为幂指数，γ＞０。 目前国 内外大部分复杂网络模型以 γ作为刻画复杂网络异质性的重 要指标，γ越小网络的异质性越强。 ＢＡ 模型中 γ值为 ３，大部 分真实网络 γ取值在 ２ ～３［１０］。 但是本文中的复杂网络模型 节点度分布并不是精确满足幂律函数，在空间引力系数 b 与边 权演化系数 λ小幅变动的情况下，如果使用拟合的方式得到 近似的 γ将难以准确描述网络结构异质性的变化。 因此本文 采用基尼系数，作为刻画复杂网络异质性的统计方法。 王林等 人在文献［１１］中详细论述了采用基尼系数来衡量复杂网络的 异质性的方法，本文将不再赘述。 本文将从复杂网络节点度分 布、距离分布、节点规模分布三方面进行数值仿真分析，以揭示 模型中的空间、边权演化、节点规模三种因素对复杂网络结构 异质性的影响作用。 2畅1　节点度值分布 计量，本文引入衡量经济社会中个人收入分配不均程度的基尼 系数指标，对复杂网络中各节点度值分布的不均程度进行衡量。 因此定义 G（K）为反映网络中各节点度值分布不均匀性的基尼 系数，并在数值仿真中分析空间引力系数 b 与边权演化系数 λ 对 G（K）的影响作用。 如图２（ａ）所示，当 b 为定值时 G（K）与 λ 是幂律函数曲线关系；如图２（ｂ） 所示，当 λ为定值，b ＜０ 时，G （K）与 b 呈指数函数曲线关系，而 b ＞０ 时，函数曲线迅速收敛。 值得注意的是，在图２（ｂ）的仿真结果中，各节点度值的基尼系 数下限收敛于０．３３，上限收敛于０．５，该基尼系数范围对应传统 度分布的幂指数γ范围为２．４２．８［１０］，这符合大部分无标度真实 网络的研究结论。 仿真结果从一个侧面能解释，为什么大部分真实网络的度 分布存在无标度性。 根据图２（ｂ）的仿真结果，复杂网络中，虽 然空间距离因素、边权演化因素对真实网络演化过程的影响作 复杂网络的度值分布是反映网络拓扑结构异质性的重要统 

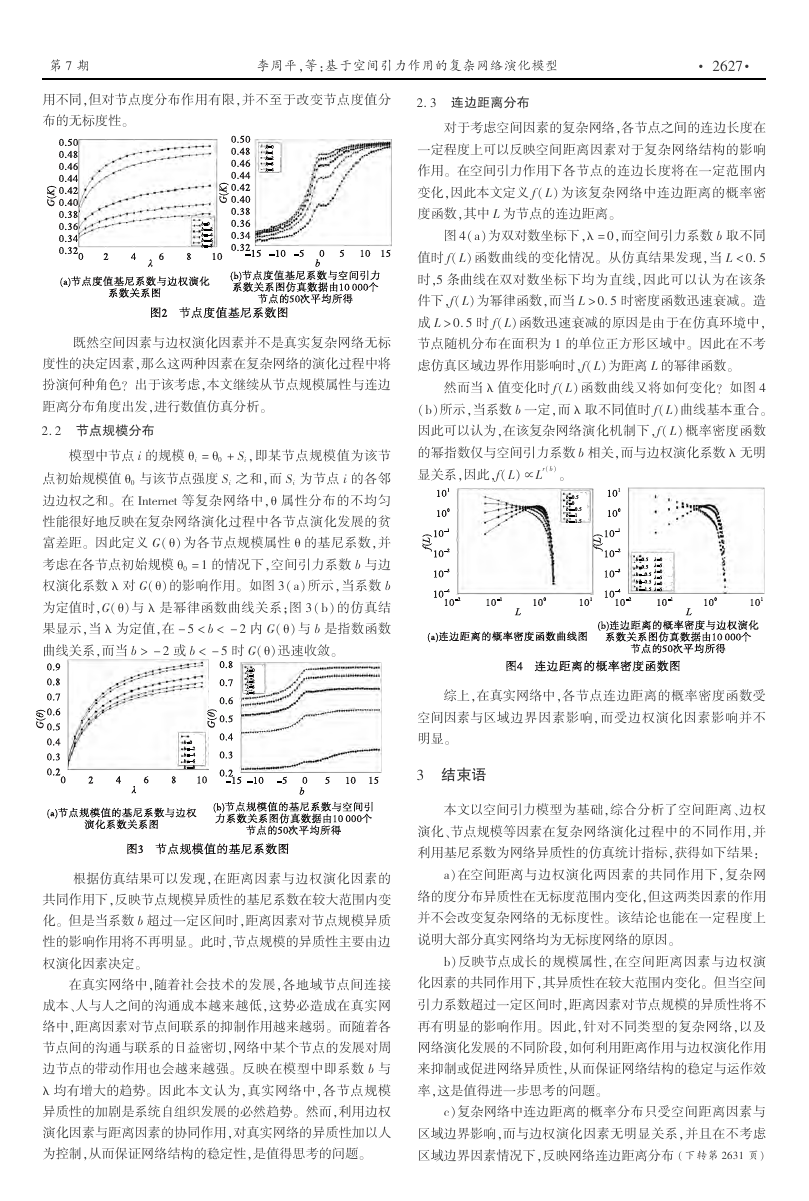
第 ７ 期 用不同，但对节点度分布作用有限，并不至于改变节点度值分 布的无标度性。 李周平，等：基于空间引力作用的复杂网络演化模型 ·７２６２· 　　　 2畅3　连边距离分布 一定程度上可以反映空间距离因素对于复杂网络结构的影响 对于考虑空间因素的复杂网络，各节点之间的连边长度在 作用。 在空间引力作用下各节点的连边长度将在一定范围内 变化，因此本文定义 f（L） 为该复杂网络中连边距离的概率密 度函数，其中 L 为节点的连边距离。 图４（ａ）为双对数坐标下，λ＝０，而空间引力系数 b 取不同 值时 f（L） 函数曲线的变化情况。 从仿真结果发现，当 L ＜０．５ 时，５ 条曲线在双对数坐标下均为直线，因此可以认为在该条 件下，f（L）为幂律函数，而当 L ＞０．５ 时密度函数迅速衰减。 造 成 L ＞０．５ 时 f（L）函数迅速衰减的原因是由于在仿真环境中， 节点随机分布在面积为１ 的单位正方形区域中。 因此在不考 虑仿真区域边界作用影响时，f（L）为距离 L 的幂律函数。 然而当 λ值变化时 f（L） 函数曲线又将如何变化？ 如图 ４ （ｂ）所示，当系数 b 一定，而 λ取不同值时 f（L）曲线基本重合。 因此可以认为，在该复杂网络演化机制下，f（L） 概率密度函数 的幂指数仅与空间引力系数 b 相关，而与边权演化系数λ无明 显关系，因此，f（L）∝Lr（b）。 既然空间因素与边权演化因素并不是真实复杂网络无标 度性的决定因素，那么这两种因素在复杂网络的演化过程中将 扮演何种角色？ 出于该考虑，本文继续从节点规模属性与连边 距离分布角度出发，进行数值仿真分析。 2畅2　节点规模分布 模型中节点 i 的规模 θi ＝θ０ ＋Si，即某节点规模值为该节 点初始规模值 θ０ 与该节点强度 Si 之和，而 Si 为节点 i 的各邻 边边权之和。 在 Ｉｎｔｅｒｎｅｔ 等复杂网络中，θ 属性分布的不均匀 富差距。 因此定义 G（θ） 为各节点规模属性 θ 的基尼系数，并 考虑在各节点初始规模 θ０ ＝１ 的情况下，空间引力系数 b 与边 权演化系数 λ对 G（θ）的影响作用。 如图３（ａ）所示，当系数 b 为定值时，G（θ）与 λ是幂律函数曲线关系；图 ３（ｂ） 的仿真结 果显示，当 λ为定值，在 －５ ＜b ＜－２ 内 G（θ） 与 b 是指数函数 曲线关系，而当 b ＞－２ 或 b ＜－５ 时 G（θ）迅速收敛。 性能很好地反映在复杂网络演化过程中各节点演化发展的贫 综上，在真实网络中，各节点连边距离的概率密度函数受 空间因素与区域边界因素影响，而受边权演化因素影响并不 明显。 3　结束语 本文以空间引力模型为基础，综合分析了空间距离、边权 演化、节点规模等因素在复杂网络演化过程中的不同作用，并 利用基尼系数为网络异质性的仿真统计指标，获得如下结果： ａ）在空间距离与边权演化两因素的共同作用下，复杂网 络的度分布异质性在无标度范围内变化，但这两类因素的作用 并不会改变复杂网络的无标度性。 该结论也能在一定程度上 说明大部分真实网络均为无标度网络的原因。 ｂ）反映节点成长的规模属性，在空间距离因素与边权演 化因素的共同作用下，其异质性在较大范围内变化。 但当空间 引力系数超过一定区间时，距离因素对节点规模的异质性将不 再有明显的影响作用。 因此，针对不同类型的复杂网络，以及 网络演化发展的不同阶段，如何利用距离作用与边权演化作用 来抑制或促进网络异质性，从而保证网络结构的稳定与运作效 率，这是值得进一步思考的问题。 ｃ）复杂网络中连边距离的概率分布只受空间距离因素与 区域边界影响，而与边权演化因素无明显关系，并且在不考虑 区域边界因素情况下，反映网络连边距离分布 （ 下转第 ２６３１ 页） 根据仿真结果可以发现，在距离因素与边权演化因素的 共同作用下，反映节点规模异质性的基尼系数在较大范围内变 化。 但是当系数 b 超过一定区间时，距离因素对节点规模异质 性的影响作用将不再明显。 此时，节点规模的异质性主要由边 权演化因素决定。 在真实网络中，随着社会技术的发展，各地域节点间连接 成本、人与人之间的沟通成本越来越低，这势必造成在真实网 络中，距离因素对节点间联系的抑制作用越来越弱。 而随着各 节点间的沟通与联系的日益密切，网络中某个节点的发展对周 边节点的带动作用也会越来越强。 反映在模型中即系数 b 与 λ均有增大的趋势。 因此本文认为，真实网络中，各节点规模 异质性的加剧是系统自组织发展的必然趋势。 然而，利用边权 演化因素与距离因素的协同作用，对真实网络的异质性加以人 为控制，从而保证网络结构的稳定性，是值得思考的问题。 

第 ７ 期 姚玉坤，等：基于 ＭＡＯＤＶ 协议的网络编码方案 5畅2畅2　网络能量消耗 网络编码的直接效益就是数据包发送总数的减少，而数据 包发送总数与能量消耗直接相关，数据包总数的减少即可以减 小能耗。 图７ 为在仿真的１ ０００ ｓ 时间内，基于网络编码的 Ａｄ ｈｏｃ 网络与普通 Ａｄ ｈｏｃ 网络的能量消耗的对比。 可以看出，基 于网络编码的 Ａｄ ｈｏｃ 网络的能量消耗要比普通 Ａｄ ｈｏｃ 网络 少。 这说明了提出的网络编码策略能够有效地减少 Ａｄ ｈｏｃ 组 播网络的能量消耗，达到了节能的目的。 5畅2畅3　数据传送成功率 图８ 显示了普通Ａｄ ｈｏｃ 网络和基于网络编码的Ａｄ ｈｏｃ 网 络中的数据传送效果。 可以明显看出，在多个仿真场景中，基 于网络编码的 Ａｄ ｈｏｃ 网络的数据发送成功率不低于普通 Ａｄ ｈｏｃ 网络的成功率，说明所设计的网络编码策略能够保障数据 传送性能。 络中使用网络编码的网络编码策略和网络编码处理策略的实 6　结束语 本文将网络编码和由 ＭＡＯＤＶ 协议搭建的 Ａｄ ｈｏｃ 组播网 络结合起来，立足于网络编码在 Ａｄ ｈｏｃ 组播网络中的具体应 用研究，提出了一种在由 ＭＡＯＤＶ 协议组建的 Ａｄ ｈｏｃ 组播网 施方案，以深入研究网络编码对 Ａｄ ｈｏｃ 组播网络性能的具体 改进。 通过在 ＯＰＮＥＴ 平台上的仿真实验验证表明，使用网络编 （ 上接第 ２６２７ 页） 的概率密度函数服从幂律分布。 参考文献： ［１］ ＡＬＢＥＲＴ Ｒ， ＪＥＯＮＧ Ｈ， ＢＡＲＡＡＳＩ Ａ Ｌ．Ｉｎｔｅｒｎｅｔ： ｄｉａｍｅｔｅｒ ｏｆ ｔｈｅ ｗｏｒｌｄ唱ｗｉｄｅ Ｗｅｂ［Ｊ］．Nature，１９９９，401（６７４９）：１３０唱１３１． ［２］ ＢＡＲＲＡＴ Ａ， ＢＡＲＴＨＥＬＥＭＹ Ｍ， ＶＥＳＰＩＧＮＡＮＩ Ａ．Ｔｈｅ ｅｆｆｅｃｔｓ ｏｆ ｓｐａｔｉａｌ ｃｏｎｓｔｒａｉｎｔｓ ｏｎ ｔｈｅ ｅｖｏｌｕｔｉｏｎ ｏｆ ｗｅｉｇｈｔｅｄ ｃｏｍｐｌｅｘ ｎｅｔｗｏｒｋｓ［Ｊ］． Journal of Statistical Mechanics： Theory and Experiment，２００５ （５）：０５００３． ［３］ ＸＵＬＶＩ唱ＢＲＵＮＥＴ Ｒ，ＳＯＫＯＬＯＶ Ｉ Ｍ．Ｇｒｏｗｉｎｇ ｎｅｔｗｏｒｋｓ ｕｎｄｅｒ ｇｅｏ唱 ｇｒａｐｈｉｃａｌ ｃｏｎｓｔｒａｉｎｔｓ［Ｊ］．Physical Review E，２００７，75（４）：４６１１７． ［４］ ＷＡＲＲＥＮ Ｃ Ｐ，ＳＡＮＤＥＲ Ｌ Ｍ，ＳＯＫＯＬＯＶ Ｉ Ｍ．Ｇｅｏｇｒａｐｈｙ ｉｎ ａ ｓｃａｌｅ唱 ｆｒｅｅ ｎｅｔｗｏｒｋ ｍｏｄｅｌ［Ｊ］．Physical Review E，２００２，66（５）：５６１０５． ［５］ ＹＯＯＫ Ｓ Ｈ，ＪＥＯＮＧ Ｈ，ＢＡＲＡＡＳＩ Ａ Ｌ，et al．Ｗｅｉｇｈｔｅｄ ｅｖｏｌｖｉｎｇ ｎｅｔ唱 ｗｏｒｋｓ［Ｊ］．Physical Review Letters，２００１，86（２５）：５８３５唱５８３８． Trans on Information Theory，２０００，46（４）：１２０４唱２１６． ·１３６２· 　　　 码后，基于 ＭＡＯＤＶ 协议的组播网络在不影响数据传送成功率 的情况下，减少了整个网络的数据包总发送次数和能量消耗。 参考文献： ［１］ ＡＨＬＳＷＥＤＥ Ｒ， ＮＩＮＧ Ｃａｉ．Ｎｅｔｗｏｒｋ ｉｎｆｏｒｍａｔｉｏｎ ｆｌｏｗ ［Ｊ］．IEEE ［２］ ＬＩ Ｓ Ｙ Ｒ， ＹＥＵＮＧ Ｒ Ｗ， ＮＩＮＧ Ｃａｉ．Ｌｉｎｅａｒ ｎｅｔｗｏｒｋ ｃｏｄｉｎｇ［Ｊ］． IEEE Tran on Information Theory，２００３，49（２）：３７１唱３８１． ［３］ ＴＲＡＣＥＹ Ｈ， ＢＥＮ Ｌ， ＫＯＥＴＴＥＲ Ｒ．Ｂｙｚａｎｔｉｎｅ ｍｏｄｉｆｉｃａｔｉｏｎ ｄｅｔｅｃｔｉｏｎ ｉｎ ｍｕｌｔｉｃａｓｔ ｎｅｔｗｏｒｋｓ ｗｉｔｈ ｒａｎｄｏｍ ｎｅｔｗｏｒｋ ｃｏｄｉｎｇ［Ｊ］．IEEE Transa on Information Theory，２００８，54（１６）：２７９８唱２８０３． ［４］ ＥＲＥＺ Ｅ， ＦＥＤＥＲ Ｍ．Ｅｆｆｉｃｉｅｎｔ ｎｅｔｗｏｒｋ ｃｏｄｅ ｄｅｓｉｇｎ ｆｏｒ ｃｙｃｌｉｃ ｎｅｔ唱 ｗｏｒｋｓ［Ｊ］．IEEE Trans on Information Theory，２０１０， 56 （８）： ３８６２唱３８７８． ［５］ ＣＨＩ Ｋａｉ唱ｋａｉ， ＪＩＡＮＧ Ｘｉａｏ唱ｈｏｎｇ， ＧＵＯ Ｍｉｎ唱ｙｉ ．Ｔｏｐｏｌｏｇｙ ｄｅｓｉｇｎ ｏｆ ｎｅｔｗｏｒｋ唱ｃｏｄｉｎｇ唱ｂａｓｅｄ ｍｕｌｔｉｃａｓｔ ｎｅｔｗｏｒｋｓ［Ｊ］．IEEE Trans on Paral唱 lel and Distributed Systems，２００８，19（５）：６２７唱６４０． ［６］ ＫＡＴＴＩ Ｓ， ＲＡＨＵＡＬ Ｈ， ＨＵ Ｗｅｎ唱ｊｕｎ， et al．ＸＯＲｓ ｉｎ ｔｈｅ ａｉｒ： ｐｒａｃ唱 ｔｉｃａｌ ｗｉｒｅｌｅｓｓ ｎｅｔｗｏｒｋ ｃｏｄｉｎｇ［Ｊ］．IEEE／ACM Trans on Networ唱 king，２００８，16（３）：４９７唱５１０． ［７］ ＺＨＡＯ Ｆａｎｇ， ＭＥＤＡＲＤ Ｍ．Ｏｎ ａｎａｌｙｚｉｎｇ ａｎｄ ｉｍｐｒｏｖｉｎｇ ＣＯＰＥ ｐｅｒ唱 ｆｏｒｍａｎｃｅ［Ｃ］ ／／Ｐｒｏｃ ｏｆ Ｉｎｆｏｒｍａｔｉｏｎ Ｔｈｅｏｒｙ ａｎｄ Ａｐｐｌｉｃａｔｉｏｎｓ Ｗｏｒｋ唱 ｓｈｏｐ．２０１０：１唱６． ［８］ ＦＲＡＧＯＵＬＩ Ｃ， ＷＩＤＭＥＲ Ｊ， ＢＯＵＤＥＣ Ｊ Ｙ Ｌ．Ｅｆｆｉｃｉｅｎｔ ｂｒｏａｄｃａｓｔｉｎｇ ｕｓｉｎｇ ｎｅｔｗｏｒｋ ｃｏｄｉｎｇ ［ Ｊ］．IEEE／ACM Trans on Networking， ２００８，16（２）：４５０唱４６３． ［９］ ＹＡＮＧ Ｓｈｕ唱ｈｕｉ， ＷＵ Ｊｉｅ．Ｅｆｆｉｃｉｅｎｔ ｂｒｏａｄｃａｓｔｉｎｇ ｕｓｉｎｇ ｎｅｔｗｏｒｋ ｃｏｄｉｎｇ ａｎｄ ｄｉｒｅｃｔｉｏｎａｌ ａｎｔｅｎｎａｓ ｉｎ ＭＡＮＥＴｓ［Ｊ］．IEEE Trans on Parallel and Distributed Systems，２０１０，21（２）：１４８唱１６１． ［１０］ ＳＴＯＩＡＮ Ｒ， ＰＥＲＩＳＯＡＲＡ Ｌ Ａ， ＳＴＯＩＣＡ Ｒ．ＩＳＳＣＳ ２００９ ｉｎｔｅｒｎａｔｉｏｎａｌ ｓｙｍｐｏｓｉｕｍ ｏｎ ｓｉｇｎａｌｓ， ｃｉｒｃｕｉｔｓ ａｎｄ ｓｙｓｔｅｍｓ［Ｃ］．２００９：１唱４． ［１１］ 殷剑宏，吴开亚．图论及其算法［Ｍ］．合肥： 中国科学技术大学出 版社，２００５． ［１２］ ＴＡＮＧ Ｈｏｎｇ， ＸＵＥ Ｆｅｉ， ＨＵＡＮＧ Ｐｅｎｇ．ＭＰ唱ＭＡＯＤＶ：ａ ＭＡＯＤＶ唱 ｂａｓｅｄ ｍｕｌｔｉ ｐａｔｈ ｒｏｕｔｉｎｇ ａｌｇｏｒｉｔｈｍ［Ｃ］ ／／Ｐｒｏｃ ｏｆ ＩＦＩＰ Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ Ｎｅｔｗｏｒｋ ａｎｄ Ｐａｒａｌｌｅｌ Ｃｏｍｐｕｔｉｎｇ．２００８：２９６唱３０１． ［６］ ＢＡＲＲＡＴ Ａ，ＢＡＲＴＨＥＬＥＭＹ Ｍ，ＶＥＳＰＩＧＮＡＮＩ Ａ．Ｍｏｄｅｌｉｎｇ ｔｈｅ ｅｖｏ唱 ｌｕｔｉｏｎ ｏｆ ｗｅｉｇｈｔｅｄ ｎｅｔｗｏｒｋｓ［Ｊ］．Physical Review E，２００４，70（６）： ６６１４９． ［７］ ＳＥＲＶＥＤＩＯ Ｖ Ｄ Ｐ，ＣＡＬＤＡＲＥＬＬＩ Ｇ，ＢＵＴＴＡ Ｐ．Ｖｅｒｔｅｘ ｉｎｔｒｉｎｓｉｃ ｆｉｔ唱 ｎｅｓｓ： ｈｏｗ ｔｏ ｐｒｏｄｕｃｅ ａｒｂｉｔｒａｒｙ ｓｃａｌｅ唱ｆｒｅｅ ｎｅｔｗｏｒｋｓ［Ｊ］．Physical Re唱 view E，２００４，70（５）：５６１２６． ［８］ ＧＡＲＬＡＳＣＨＥＬＬＩ Ｄ，ＬＯＦＦＲＥＤＯ Ｍ Ｉ．Ｆｉｔｎｅｓｓ唱ｄｅｐｅｎｄｅｎｔ ｔｏｐｏｌｏｇｉｃａｌ ｐｒｏｐｅｒｔｉｅｓ ｏｆ ｔｈｅ ｗｏｒｌｄ ｔｒａｄｅ Ｗｅｂ［Ｊ］．Physical Review Letters， ２００４，93（１８）：１８８７０１． ［９］ 闫卫阳， 王发曾，秦耀辰．城市空间相互作用理论 模 型 的 演 进 与 机理［Ｊ］．地理科学进展， ２００９，28（４）：５１１唱５１８． ［１０］ 王林，戴冠中．复杂网络的度分布研 究［Ｊ］．西北工业大学学报， ２００６，24（４）：４０５唱４０９． ［１１］ 王林， 戴冠中，胡海波．无标度网络 的一个新的拓扑参数［Ｊ］．系 统工程理论与实践， ２００６，26（６）：４９唱５３．