复高斯分布 1. 一维复高斯随机变量 如果实随机变量 X 和 Y 都服从高斯分布，而且是不相关的（这时也是独立的），均值分别为 mx 和 my，方 差都为σ2，则其联合概率密度函数（probability density function，pdf）为： p XY  , x y   1   2 2  exp            x m  x 2  y m  2   2  2  y         (1) 对应的复随机变量 Z=X+iY 则称为复高斯随机变量。Z 的均值 mz 和方差 2 z 分别为： mz  E Z    E X   iY   E X    iE Y    m x  im y (2) E Z m      z E X m   2  x     *   Z-m  z      E Y m  E y X m  x    i Y m  y  2    (3)     2      2 z          2  2 特殊的，当均值mx和my均为 0 时，复随机变量Z称为（零均值）循环对称复高斯(Zero Mean Circular Symmetric Complex Gaussian, ZMCSCG)随机变量 1 。σ2 称为Z的每个实数维上的方差(variance per real dimension)。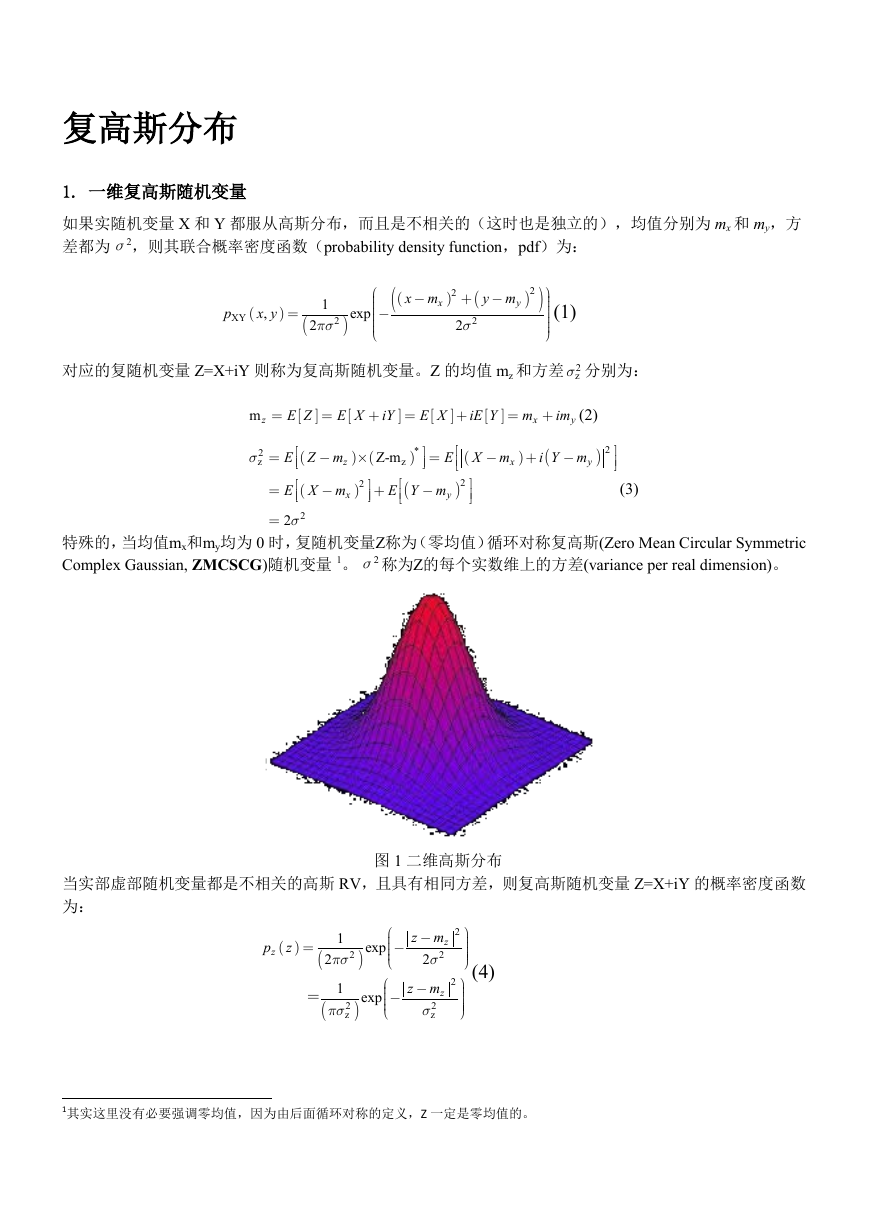 当实部虚部随机变量都是不相关的高斯 RV，且具有相同方差，则复高斯随机变量 Z=X+iY 的概率密度函数 为： 图 1 二维高斯分布 p z z     2 2  exp            z z m  2 2  z m  2  z z 2           2 (4) 1  1  2 z ＝   exp  1其实这里没有必要强调零均值，因为由后面循环对称的定义，Z 一定是零均值的。 

可以看出，当用实部＋i 虚部的方式来表示复数后，(4)式和(1)式其实是等同的。但是更加紧凑（更像一个“一 维”的随机变量的概率密度函数）。但是在计算期望进行积分的时候，还是要对实部虚部来进行积分（利用 (1)式）。这也适用于多维复随机变量的情况。 2. 复高斯随机矢量 首先补充一下循环对称(Circular Symmetric，或 CS)的含义([2], sec 2.6-1)：如果复随机矢量 Z 满足：以任意 角度旋转后，所获得的新矢量跟原矢量有相同的概率密度函数，则称复随机矢量 Z 为循环对称的。即  , e jZ 和 Z 的概率密度函数相同。显然，由此定义可以推出： E[Z]=0, E[ZZt]=0(5) 当 Z 为高斯随机矢量时，循环对称条件跟(5)等价。特别的，且当 Z 为一维时，E[Z2]=0。 故，对于 d 维的复高斯随机矢量 Z=X+iY (粗体表示列矢量)，当其满足 C = C C = C YX (6) XY  X Y , 时([2]称这样的 Z 是 proper 的,即满足 E[(Z-mZ)(Z-mZ)t)]=0)，新随机矢量 Z-mZ 是循环对称（对于复随机矢 量，零均值＋proper 条件即对应循环对称）的，变量代换后的概率密度函数为 p z    1 d    Σ exp        H z mΣz m   z 1    2  z      (7) 其中, mz=E[z] 是随机矢量 z 的均值, Σ=E[(z-mz)(z-mz)H] 是互协方差矩阵（假设非奇异）, |Σ|是 Σ 的行列式， zH 表示 z 的共轭转置. 如果这个复高斯随机矢量 Z 不是 proper 的，则其概率密度函数不能这样表示，而应以对应的 2d 维实随机矢 量的联合分布来表示： z p( )  p z ( )   1 d   2  C z  exp  － 1 2  其中 z m C z m      t  z  z    z  (8) Z  X X 1 , 2 ,..., 且 Ezm z ＝ 。   , X Y Y 2 , d 1 ,..., Y d t  (9) 幸运的是，在大多数应用环境下，我们都可以假设复随机矢量 Z－mz 为循环对称的，甚至可以假设 Z 本身 就是循环对称的。 当对复高斯随机变量取模时，可以得到另两种特殊的分布：瑞利分布(Rayleigh distribution)和莱斯分布（Rice distribution）。 设有复高斯随机变量 z=x+iy，令 a=|E[z]|，σ2=E[|z|2]，则 r=|z|的 pdf 可以通过坐标变换：x=r cosθ, y=rsinθ,并 求边缘分布来获得。 ·当 a=0 时，r 的 pdf 为瑞利分布： (10)  0 p r   exp , r   2      r 2             r 2  2       ·当 a>0 时，r 的 pdf 为莱斯分布： 

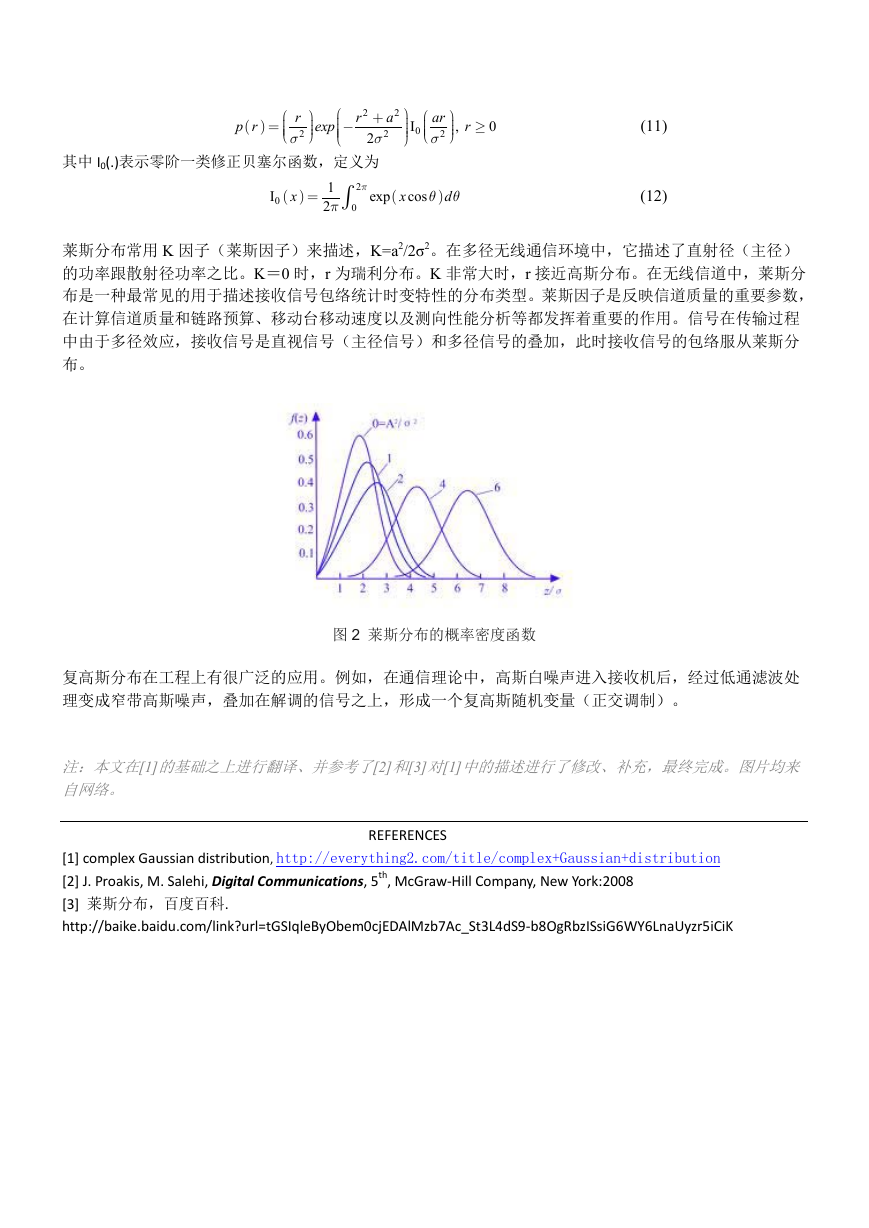
 2 2      2   其中 I0(.)表示零阶一类修正贝塞尔函数，定义为 r 2  p r   a 2 exp             r       I 0      ar 2       , r  0 I 0 x    1 2   2  0 exp  x cos   d  (11) (12) 莱斯分布常用 K 因子（莱斯因子）来描述，K=a2/2σ2。在多径无线通信环境中，它描述了直射径（主径） 的功率跟散射径功率之比。K＝0 时，r 为瑞利分布。K 非常大时，r 接近高斯分布。在无线信道中，莱斯分 布是一种最常见的用于描述接收信号包络统计时变特性的分布类型。莱斯因子是反映信道质量的重要参数， 在计算信道质量和链路预算、移动台移动速度以及测向性能分析等都发挥着重要的作用。信号在传输过程 中由于多径效应，接收信号是直视信号（主径信号）和多径信号的叠加，此时接收信号的包络服从莱斯分 布。 图 2 莱斯分布的概率密度函数 复高斯分布在工程上有很广泛的应用。例如，在通信理论中，高斯白噪声进入接收机后，经过低通滤波处 理变成窄带高斯噪声，叠加在解调的信号之上，形成一个复高斯随机变量（正交调制）。 注：本文在[1]的基础之上进行翻译、并参考了[2]和[3]对[1]中的描述进行了修改、补充，最终完成。图片均来 自网络。 [1] complex Gaussian distribution, http://everything2.com/title/complex+Gaussian+distribution [2] J. Proakis, M. Salehi, Digital Communications, 5th, McGraw-Hill Company, New York:2008 [3] 莱斯分布，百度百科. http://baike.baidu.com/link?url=tGSIqleByObem0cjEDAlMzb7Ac_St3L4dS9-b8OgRbzISsiG6WY6LnaUyzr5iCiK REFERENCES