第1页 / 共8页
第2页 / 共8页
第3页 / 共8页
第4页 / 共8页
第5页 / 共8页
第6页 / 共8页
第7页 / 共8页
第8页 / 共8页
2007年宁夏石嘴山中考数学真题及答案.doc
2007 年宁夏石嘴山中考数学真题及答案
注意事项：
1． 考试时间 120 分钟，全卷总分 120 分．
2． 答题前将密封线内的项目填写清楚．
3． 答卷一律使用黑、蓝钢笔或圆珠笔．
4． 凡使用答题卡的考生，答卷前务必将答题卡上有关项目填写清楚．选择题的每小题选出
答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再
选涂其他答案．不使用答题卡的考生，将选择题的答案答在试卷上．
一、选择题（下列每小题所给的四个答案中只有一个是正确的，每小题 3 分，共 24 分）
1． 2 的相反数是（
C． 2
D．2
A．
1
2
）
1
2
B．
2．下列运算正确的是（
）
A． 2
a a
3
6
a
B． 8
a
4
a
2
a
C．
(
)ab
2
2
ab
D． 3
a
3
a
32
a
3．某校对 1200 名女生的身高进行了测量，身高在1.58 ~ 1.63 （单位：m）这一小组的频率
为 0.25，则该组的人数为（
A．150 人
B．300 人
4．2006 年国家统计局发布的数据表明，我国义务教育阶段在校学生人数共 16700 万人，用
科学记数法表示为（
C．600 人
D．900 人
）
）
A．
1.67 10 人 B．
6
1.67 10 人 C．
7
1.67 10 人 D．
8
1.67 10 人
9
5．下列图形中，即是中心对称图形又是轴对称图形的是（
A．等边三角形 B．菱形
6．如图， PA 为 O 的切线， A 为切点， PO 交 O 于点
B ，
，则sin AOP
4
，
C．等腰梯形
的值为（
OA
PA
）
3
）
D．平行四边形
A
P
B
O
A．
3
4
B．
3
5
C．
4
5
D．
4
3
7．如图，下列选项中不是．．正六棱柱三视图的是（
）
A．
B．
C．
D．
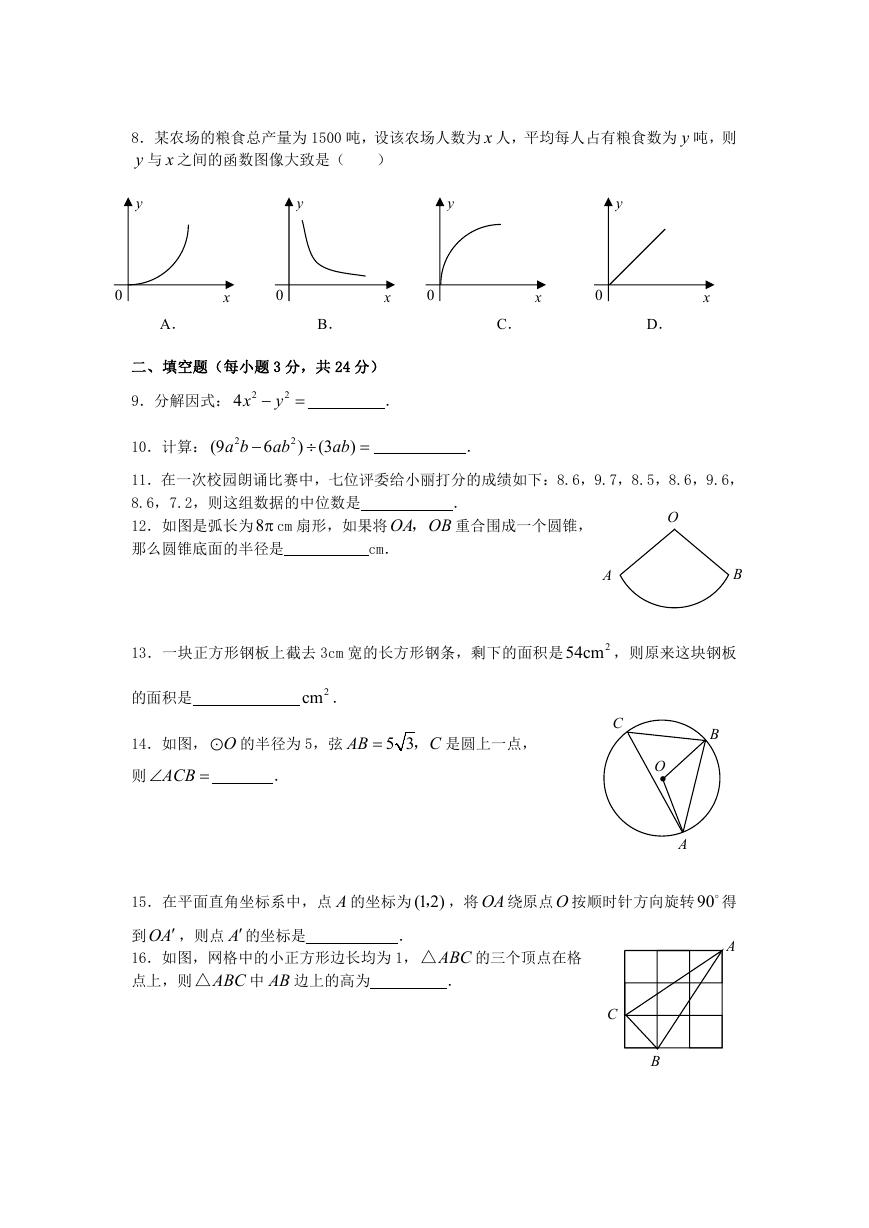
8．某农场的粮食总产量为 1500 吨，设该农场人数为 x 人，平均每人占有粮食数为 y 吨，则
y 与 x 之间的函数图像大致是（
）
y
y
y
y
0
x
0
x
0
x
0
x
A．
B．
C．
D．
二、填空题（每小题 3 分，共 24 分）
9．分解因式： 2
4x
2
y
．
10．计算： 2
a b
(9
2
6
ab
)
(3
ab
)
．
11．在一次校园朗诵比赛中，七位评委给小丽打分的成绩如下：8.6，9.7，8.5，8.6，9.6，
8.6，7.2，则这组数据的中位数是
12．如图是弧长为8 cm 扇形，如果将 OA OB， 重合围成一个圆锥，
那么圆锥底面的半径是
cm．
．
O
A
B
13．一块正方形钢板上截去 3cm 宽的长方形钢条，剩下的面积是
54cm ，则原来这块钢板
2
的面积是
2cm ．
14．如图， O 的半径为 5，弦
则 ACB
．
AB
， 是圆上一点，
5 3
C
C
B
O
A
15．在平面直角坐标系中，点 A 的坐标为 (1 2)， ，将 OA 绕原点O 按顺时针方向旋转90 得
到OA ，则点 A 的坐标是
16．如图，网格中的小正方形边长均为 1， ABC△
点上，则 ABC△
．
中 AB 边上的高为
的三个顶点在格
．
A
C
B
三、解答题（共 24 分）
17．（6 分）
计算：
( 9)
0
3
64
5
1
2
2
．
18．（6 分）
解分式方程：
19．（6 分）
1
2
x
2
3
x
．
解不等式组
x
1
2
x
2
≥
0
x
，并利用数据表示不等式组的解集．
0
1
2
3
4
x
20．（6 分）
A B， 两个口袋中，都装有三个相同的小球，分别标有数字 1，2，3，小刚、小丽两人进行
摸球游戏．游戏规则是：小刚从 A 袋中随机摸一个球，同时小丽从 B 袋中随机摸一个球，
当两个球上所标数字之和为奇数时小刚赢，否则小丽赢．这个游戏对双方公平吗？通过列表
或画树状图加以说明．
四、解答题（共 48 分）
21．（6 分）
二次函数
y
2
ax
bx
(
c a
表：
， ， ， 是常数 ) 中，自变量 x 与函数 y 的对应值如下
a b c
0
1
1
2
1
3
（1）判断二次函数图象的开口方向，并写出它的顶点坐标．
（2）一元二次方程 2
ax
bx
c
0(
a
， ， ， 是常数 ) 的两个根 1
x
a b c
0
x， 的取值范围
2
是下列选项中的哪一个
．
①
③
1
2
1
2
x
2
30
，
2
0 2
，
x
2
x
1
x
1
2
5
2
②
1
x
1
④
1
x
1
x
2
1
2
，
2
1 3
，
2 2
x
2
5
2
2
22．（6 分）
通过对全区 2004 年至 2006 年旅游景点发展情况的调查，制成了全区旅游景点个数情况的条
形统计图和每年旅游景点游客人数平均数情况的条形统计图，利用这两张统计图提供的信
息，解答下列问题．
景点个数
50
39
30
万人/个
3.0
2.5
2.0
2004
2005
2006
年份
2004
2005
2006
年份
旅游景点个数情况的条形统计图
每年旅游景点游客人数平均数
情况的条形统计图
（1）这三年接待游客最多的年份是哪一年？
（2）这三年中平均每年接待游客多少人？
23．（8 分）
如图，将矩形纸片 ABCD 沿对角线 BD 折叠，点C 落在点 E 处， BE 交 AD 于点 F ，连结
AE ．
证明：（1） BF DF
（2） AE
BD∥ ．
．
E
F
A
D
B
C
24．（8 分）
某家庭装修房屋，由甲、乙两个装修公司合作完成，选由甲装修公司单独装修 3 天，剩下的
工作由甲、乙两个装修公司合作完成．工程进度满足如图所示的函数关系，该家庭共支付工
资 8000 元．
（1）完成此房屋装修共需多少天？
（2）若按完成工作量的多少支付工资，甲装修公司应得多少元？
y（工作量）
0
3
5
x（天）
25．（10 分）
现代家居设计的“推拉式”钢窗，运用了轨道滑行技术，纱窗装卸时利用了平等四边形的不
稳定性，操作步骤如下：
（1）将矩形纱窗转化成平行四边形纱窗后，纱窗上边框嵌入窗框的上轨道槽（如图 1）．
（2）将平行四边形纱窗的下边框对准窗框的下轨道槽（如图 2）．
（3）将平行四边形纱窗还原成矩形纱窗，同时下边框嵌入窗框的下轨道槽（如图 3）．
在装卸纱窗的过程中，如图所示 的值不得小于81 ，否则纱窗受损．现将高 96cm 的矩
形纱窗恰好安装在上、下槽深分别为 0.9cm，高 96cm（上、下槽底间的距离）的窗框上．试
求合理安装纱窗时 的最大整数值．（下表提供的数据可供使用）
图 1
图 2
图 3
26．（10 分）
如图，在平面直角坐标系中，等腰梯形 AOBC 的四个顶点坐标分别为 (2 2 3)
A ， ， (0 0)
O ，，
(8 0)
(6 2 3)
C，， ， ．
B
（1）求等腰梯形 AOBC 的面积．
（2）试说明点 A 在以OB 的中点 D 为圆心，OB 为直径的圆上．
（3）在第一象限内确定点 M ，使 MOB△
坐标．
（3）点 1M 位于点 C 上时，
与 AOB△
1OM B△
与 OAB△
相似
此时点 1M 的坐标为 1(6 2 3)
过 B 点作 OB 的垂线交 OA 的延长线于 2M ，
M ，
2OM B△
与 OAB△
相似
此时点 2M 的坐标为 2(8 8 3)
过 B 点作 OB 的垂线交 OC 的延长线于 3M ，
M ，
3OM B△
与 OAB△
相似
M
此时点 3M 的坐标为 3
8 3
8
，
3
相似，求出所有符合条件的点 M 的
y
A
C
O
B
x
一、选择题（每小题 3 分，共 24 分）
题号
答案
1
D
2
D
3
B
二、填空题（每小题 3 分，共 24 分）
11
10
题号
9
答案 (2
x
y
)(2
x
y
)
2a
3
b
8.6
参考答案
4
C
12
4
5
B
6
C
7
A
13
81
14
15
60° (2
1)，
8
B
16
或
5
13
5 13
13
x
x
24
分）
三、解答题（ 6 6 6 6
················································································ 4 分
17．解：原式 1 4 5 4
2 ············································································································· 6 分
···············································································2 分
18．解：去分母得 3 4
解方程得 1x ································································································· 4 分
经检验 1x 是原分式方程的解············································································5 分
∴原分式方程的解是 1x ··················································································6 分
x ≤ ········································································ 1 分
19．解：解不等式（1）得
x ···················································································· 3 分
解不等式（2）得
能在数轴上正确表示出不等式组的解集································································ 5 分
≤ ·········································································· 6 分
∴不等式组的解集是 1
20．解：游戏不公平·························································································1 分
能正确画出树状图或表格·················································································· 3 分
2
1
2
x
P
(
奇数
)
4
9
P
(
偶数
)
5
9
···················································································· 5 分
48
分）
小丽获胜的可能性大·························································································6 分
四、解答题（ 6 6 8 8 10 10
21．解（1）开口向下······················································································· 2 分
顶点坐标 (1 2)， ································································································· 4 分
x， 的取值范围是③····································································· 6 分
x
（2）两个根 1
22．解：（1）2004 年接待游客人数： 30 2 60
2005 年接待游客人数： 39 3 117
2006 年接待游客人数： 50 2.5 125
接待游客最多的年份是 2006 年··········································································· 3 分
（2） 2 30 3 39 50 2.5
（万人）
（万人）
（万人）
60 117 125
（万人）
2
3
100.7
3
△
≌△
EDF
EBD
（或 ABF
这三年中全区平均每年接待游客 100.7 万人·························································· 6 分
）······························ 3 分
23．解：（1）能正确说明 ADB
···································································································· 4 分
BF DF∴
（其它方法参考以上标准给分）．
）················································· 7 分
（2）能得出 AEB
∴ ∥ ···································································································· 8 分
（其它方法参考以上标准给分）．
24．（1）方法 1
解：设一次函数的解析式（合作部分）是 y
， ， 是常数）
（或 EAD
（ 0
kx b
BDA
DBE
k b
BD
AE
k
由待定系数法解得 1
8
k
，
b
∴一次函数的表达式为 1
x
8
y
．
1
8
1
8
······································································· 2 分
x
1 1
8
x ，解得 9
当 1y 时， 1
8
∴完成此房屋装修共需 9 天··············································································· 4 分
方法 2
解：由正比例函数图像可知：甲的效率是 1
12
·························································1 分
乙工作的效率： 1
1
8 12
甲、乙合作的天数： 3
4
1
24
1
12
1
24
6
（天）
··············································································· 2 分
∵甲先工作了 3 天，∴完成此房屋装修共需 9 天····················································4 分
（2）由正比例函数图象可知：甲的工作效率是 1
12
················································· 5 分
4
9
（元）···························································8 分
····································································· 7 分
甲 9 天完成的工作量是： 1
12
3
4
∴甲得到的工资是： 3 8000 6000
25．解：能够合理装上平行四边形纱窗时的最大高度： 96 0.9 95.1
能够合理装上平行四边形纱窗时的高： 96sin 或 96 cos(90
)
°
96 0.987 94.752 95.1
当
∴此时纱窗能装进去，
当
∴此时纱窗能装进去．
当
∴此时纱窗装不进去．····················································································· 9 分
因此能合理装上纱窗时 的最大值是82°··························································10 分
（cm）··············· 2 分
··························5 分
81 °时，纱窗高： 96sin81
82 °时，纱窗高： 96sin82
83 °时，纱窗高： 96sin83
96 0.993 95.328 95.1
96 0.990 95.04 95.1
°
°
°
·
26．解：（1）
S
梯形
上底 下底 高 1 (4 8) 2 3 12 3
)
·································4 分
1 (
2
2
说明点 A 在圆上．
是直角三角形，说明点 A 在圆上．
（2）方法 1：得出 DO DA DB
OAB
方法 2：得出
方法 3：得出 2
OA
即 OAB△
（3）点 1M 位于点 C 上时，
°，即 OAB△
AB OB
90
2
1OM B△
，
2
与 OAB△
相似
是直角三角形，说明点 A 在圆上．························································· 7 分
M ， ············································································8 分
此时点 1M 的坐标为 1(6 2 3)
过 B 点作 OB 的垂线交 OA 的延长线于 2M ，
此时点 2M 的坐标为 2(8 8 3)
过 B 点作 OB 的垂线交 OC 的延长线于 3M ，
2OM B△
与 OAB△
相似
3OM B△
与 OAB△
相似
M ， ··········································································· 9 分
M
此时点 3M 的坐标为 3
8 3
， ········································································ 10 分
8
3
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
