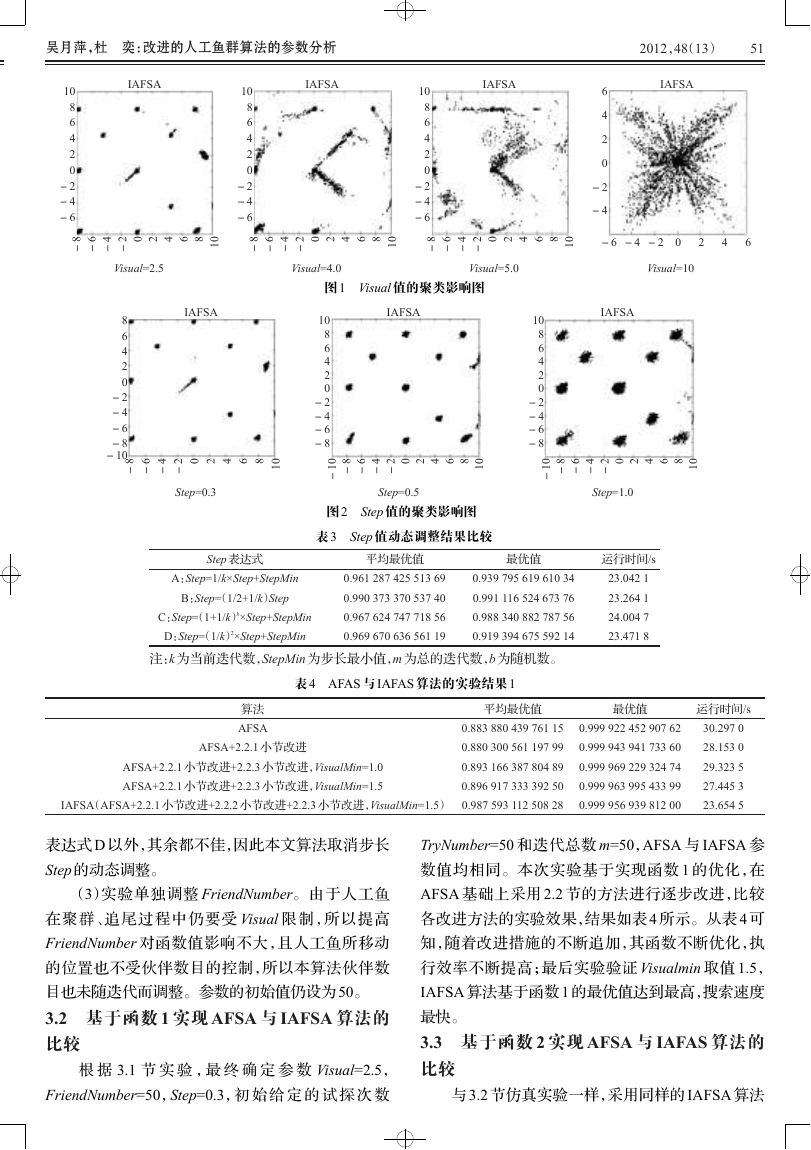
吴月萍，杜 奕：改进的人工鱼群算法的参数分析 IAFSA IAFSA 10 8 6 4 2 0 －2 －4 －6 10 8 6 4 2 0 －2 －4 －6 IAFSA 10 8 6 4 2 0 －2 －4 －6 6 4 2 0 －2 －4 2012，48（13） 51 IAFSA 8 6 4 2 0 2 4 6 8 － － － － Visual=2.5 0 1 8 6 4 － － － 2 0 2 4 6 8 － Visual=4.0 0 1 8 6 4 2 0 2 4 6 8 － － － － Visual=5.0 0 1 －6 －4 －2 0 2 4 6 Visual=10 图 1 Visual 值的聚类影响图 IAFSA 8 6 4 2 0 －2 －4 －6 －8 －10 IAFSA 10 8 6 4 2 0 －2 －4 －6 －8 IAFSA 10 8 6 4 2 0 －2 －4 －6 －8 8 － 6 － 4 － 2 0 2 4 6 8 － Step=0.3 0 1 8 － 6 － 4 － 0 1 － 2 0 2 4 6 8 － Step=0.5 0 1 8 － 6 － 4 － 0 1 － 2 0 2 4 6 8 － Step=1.0 0 1 图 2 Step 值的聚类影响图 表 3 Step 值动态调整结果比较 Step 表达式 平均最优值 最优值 A：Step=1/k×Step+StepMin B：Step=（1/2+1/k）Step C：Step=（1+1/k）b×Step+StepMin D：Step=（1/k）2×Step+StepMin 0.961 287 425 513 69 0.990 373 370 537 40 0.967 624 747 718 56 0.969 670 636 561 19 0.939 795 619 610 34 0.991 116 524 673 76 0.988 340 882 787 56 0.919 394 675 592 14 运行时间/s 23.042 1 23.264 1 24.004 7 23.471 8 注：k 为当前迭代数，StepMin 为步长最小值，m 为总的迭代数，b 为随机数。 表 4 AFAS 与 IAFAS 算法的实验结果 1 算法 AFSA AFSA+2.2.1 小节改进 AFSA+2.2.1 小节改进+2.2.3 小节改进，VisualMin=1.0 AFSA+2.2.1 小节改进+2.2.3 小节改进，VisualMin=1.5 IAFSA（AFSA+2.2.1 小节改进+2.2.2 小节改进+2.2.3 小节改进，VisualMin=1.5） 平均最优值 最优值 0.883 880 439 761 15 0.880 300 561 197 99 0.893 166 387 804 89 0.896 917 333 392 50 0.987 593 112 508 28 0.999 922 452 907 62 0.999 943 941 733 60 0.999 969 229 324 74 0.999 963 995 433 99 0.999 956 939 812 00 运行时间/s 30.297 0 28.153 0 29.323 5 27.445 3 23.654 5 表达式 D 以外，其余都不佳，因此本文算法取消步长 Step 的动态调整。 （3）实验单独调整 FriendNumber。由于人工鱼 在聚群、追尾过程中仍要受 Visual 限制，所以提高 FriendNumber 对函数值影响不大，且人工鱼所移动 的位置也不受伙伴数目的控制，所以本算法伙伴数 目也未随迭代而调整。参数的初始值仍设为 50。 3.2 基于函数 1 实现 AFSA 与 IAFSA 算法的 比较 根 据 3.1 节 实 验 ，最 终 确 定 参 数 Visual=2.5， FriendNumber=50，Step=0.3，初 始 给 定 的 试 探 次 数 TryNumber=50 和迭代总数 m=50，AFSA 与 IAFSA 参 数值均相同。本次实验基于实现函数 1 的优化，在 AFSA 基础上采用 2.2 节的方法进行逐步改进，比较 各改进方法的实验效果，结果如表 4 所示。从表 4 可 知，随着改进措施的不断追加，其函数不断优化，执 行效率不断提高；最后实验验证 Visualmin 取值 1.5， IAFSA 算法基于函数 1 的最优值达到最高，搜索速度 最快。 3.3 基于函数 2 实现 AFSA 与 IAFAS 算法的 比较 与 3.2 节仿真实验一样，采用同样的 IAFSA 算法 

52 2012，48（13） Computer Engineering and Applications 计算机工程与应用 表 5 AFAS 与 IAFAS 算法的实验结果 2 算法 平均最优值 最优值 运行时间/s 原最小值 迭代后最小值 AFSA IAFSA 2.291 150 772 509 121 E+003 3.083 480 070 041 062 E+003 3.596 369 278 384 290 E+003 3.599 512 547 387 318 E+003 24.754 500 000 000 00 22.596 800 000 000 00 5.828 732 265 503 80 5.828 732 265 503 80 47.557 043 615 810 15 60.524 403 823 872 00 对 函 数 2 进 行 优 化 ，其 中 ，Visual=1，Step=0.008， VisualMin=0.4，其他参数同上例，AFSA 与 IAFSA 参 数值均相同，实验结果如表 5 所示。从表 5 可以看 出，IAFSA 算法在函数最优值、迭代后的最小值、运 行时间上，都比 AFSA 算法得到了提高。 4 结论 本文对 AFSA 算法进行深入研究，根据 AFSA 的 原理，以及一些数学知识对 AFSA 算法进行改进；通 过仿真实验测试各参数值的影响，基于多个函数实 现了 IAFSA 算法的仿真实验，并与 AFSA 进行了比 较。实验结果表明，在合理设置参数值的前提下， IAFSA 算法能提高函数的求解精度以及人工鱼的搜 索速度。这些特性的提高，使算法更适用于各种优 化问题，例如：资源优化配置、车辆路径优化调度、解 决组合优化问题；同时也能更好地实现数据的聚类， 提高其在实现数据挖掘的其他算法中的应用，这也 是下一步值得研究的问题。 式：鱼群算法 [J].系统工程理论与实践，2002，22（11）： 32-38. [2] 李晓磊.一种新型的智能优化方法——人工鱼群算法[D]. 杭州：浙江大学，2003. [3] Xiao Jianmei，Zheng Xiaoming，Wang Xihuai，et al.A modified artificial fish-swarm algorithm[C]//Proceedings of the World Congress on Intelligent Control and Auto- mation（WCICA）.Piscataway，United States：IEEE，2006： 3456-3460. [4] 张梅凤，邵诚.多峰函数优化的生境人工鱼群算法[J].控制 理论与应用，2008，25（4）：773-776. [5] Song Zhiyu，Li Junjie，Wang Hongyu.Inverse research for gravity dam parameters based on chaos artificial fish swarm algorithm[J].Rock and Soil Mechanics， 2007，28（10）：2193-2196. [6] 王西邓.人工鱼群算法的改进研究[D].西安：西安建筑科技 大学，2007. [7] 范玉军，王冬冬，孙明明.改进的人工鱼群算法[J].重庆师范 大学学报：自然科学版，2007，24（3）：23-26. [8] 王会颖，章义刚.求解聚类问题的改进人工鱼群算法[J].计 算机技术与发展，2010，20（3）. 参考文献： [1] 李晓磊，邵之江，钱积新.一种基于动物自治体的寻优模 [9] 任子武，伞冶.自适应遗传算法的改进及在系统辨识中应 用研究[J].系统仿真学报，2006，8（1）：4l-43. （上接 43 页） of Machine Learning Research，2004（5）：1287-1330. [18] Herskovits E.Computer-based probabilistic network con- [23] Chickering D M.Learning equivalence classes of Bayes- struction[D].USA：Stanford University，1991. [19] Singh M，Valtorta M.Construction of Bayesian network structures from data：a brief survey and an efficient algo- rithm[J].International Journal of Approximate Reasoning， 1995，12（2）：111-131. [20] Heckerman D.A tutorial on learning with Bayesian net- works，Technical Report MSR-TR-95-06[R].Microsoft Research，1995. [21] Chickering D M.Learning Bayesian networks is NP- complete[D].Los Angeles：Computer science Department University of California，1994：120-225. [22] Chickering D M，Heckerman D，Meek C.Large-sample learning of Bayesian networks is NP-hard[J].Journal ian network structures[J].Journal of Machine Learning Research，2002（2）：445-498. [24] Proaki J.Digital communications[M].[S.l.]：McGraw-Hill， 2000. [25] Chickering D M.A transformational characterization of equivalent Bayesian network structures[C]//Proceedings of the 11th Conference on Uncertainty in Artificial Intelligence.San Francisco：Morgan Kaufmann，1995：87-98. the [26] Cooper D，Herskovits E.A Bayesian method for induction of probabilistic networks from data[J].Machine Learning，1992，9（4）：309-347. [27] Ronan D，Shen Qiang.Learning Bayesian equivalence classes with ant colony optimization[J].Journal of Arti- ficial Intelligence Research，2009，35：391-447.