写给新手程序员的一封信.pdf-资料库

GPS单点定位算法及实现摘要：本文主要介绍了 GPS 卫星轨道坐标计算数学模型，单点定位数学模型，并根据最小二乘原理，用 C++编写了几个小程序对 GPS 观测数据进行处理，包括时间转换程序、利用广播星历计算卫星坐标程序和地面点近似坐标计算程序。最后，选取实例进行计算并进行精度分析。关键词：GPS；单点定位；坐标计算；精度分析 1 引言 GPS是美国从20 世纪70 年代开始研制的, 于1994 年全面建成, 具有在海、陆、空进行全方位实时三维导航与定位能力的新一代卫星导航与定位系统。尤其是经过近几年的研究,GPS 更在测绘、航空遥感和气象等方面有了新的应用, 并以全天候、高精度、自动化、高效益等显著特点, 赢得广大用户的信赖。随着对定位精度要求的不断提高, 人们对GPS卫星星历的精度和实时性提出了越来越高的要求。卫星的星历, 是描述有关卫星运动轨道的信息。利用 GPS 进行定位, 就是根据已知的卫星轨道信息和用户的观测资料, 通过数据处理来确定接收机的位置及其载体的航行速度。所以, 精确的轨道信息是精密定位的基础。GPS 的卫星星历按照精度可分为精密星历和广播星历。精密星历是由国际 GPS 服务中心( IGS) 通过 Internet 发布,它的轨道精度可达到 10cm 左右, 足以满足精密定位的需要。但是精密星历只能在卫星观测的 11d 后获得, 无法为实时定位、导航、气象等实时性要求很强的应用提供有效的服务。广播星历是通过接收机接收卫星发射的含有轨道信息的导航电文, 经过解码获得的卫星星历推算得到卫星位置, 可以实现实时的导航和定位。本程序以 2009 年 11 月 21 日上海跟踪站（SHAO）的 RINEX 格式广播星历 shao3250.09n 和观测数据 shao3250.09o 为例，取了 200 个连续观测历元，在不同历元求出坐标值，最后求出坐标平差值，对平差值的各分量作比较。

2 GPS卫星轨道坐标计算数学模型广播星历就是卫星 GPS 将含有轨道信息的导航电文发送给用户接收机，然后经过解码获得的卫星星历。GPS 用户通过卫星广播星历，可以获得 16 个卫星星历参数，其中，1 个参考时刻，6 个相应参考时刻的开普勒轨道参数和 9 个摄动力影响的参数。这些参数的定义如下表所示：表 1 导航电文中的参考参数名称星历参数的参考历元轨道长半轴的方根轨道偏心率参数 nΔ Ω i 名称平均运行速度差升交点赤经变化率轨道倾角变化率参考时刻的轨道倾角 C C ,us uc 升交距角的调和改正项振幅参数 oet sa se 0i 0Ω 参考时刻的升交点赤经 C C ,is ic 轨道倾角的调和改正项振幅 sω 近地点角距 C C ,rs rc 卫星地心距的调和改正项振幅 sM 参考时刻的平近点角 AODE 星历数据的龄期其中，AODE 表示从最后一次注入电文起外推星历时 0 的外推时间间隔，它反映了外推星历的可靠程度。根据上述数据，便可外推出观测时刻 t 的轨道参数，从而计算卫星在不同参考系中的相应坐标。 2.1 用广播星历参数计算卫星位置在利用 GPS 信号进行导航定位时，为了解算用户在地心坐标系中的位置， GPS 接收机需要测定测站到卫星的距离并且要知道同一卫星在同一时刻的地心坐标[2]。卫星的地心坐标是从卫星的导航电文中提供的开普勒轨道参数和轨道摄动修正量按一定公式计算的。 1)计算卫星运行的平均角速度 n ：卫星的平均角速度用下式计算： 0n

n 0 = GM a / 3 2 (1) 式中，GM=398600.5 ( km s ) / 3 2 是WGS-84坐标系中地球引力常数。利用导航电文中给出的摄动改正数 nΔ ，用下式求卫星运行的平均角速度： n n = n 0 + Δ (2) n 2)对观测时刻做卫星钟差改正： 't t ' = − Δ t t t Δ = a 0 + a t ( 1 − t 0 e ) + a t ( 2 − 2 t )e 0 (3) 在计算卫星钟差改正时，t 可近似取。 tΔ 't 3)观测时刻的平近点角 sM 的计算： M M n t ( = + 0 s − t 0 ) e （4） 4)计算偏近点角 sE ： E M e + s s = s sin Es （5）（5）式可用迭代法进行计算，即先令 s E M= 代入上式，求出 sE 再代入上 s 式计算，由于偏心率e很小（只有0.01），因此收敛很快，只需迭代两次便可求出偏近点角。 5)真近点角的计算： ∵ cos f s = (cos E e − s s ) /(1 − e s cos E ) s sin f s = ( 1 − 2 e sin E s ) /(1 − e s cos E ) s ( E eω s s ) （6） ∴ f s = arctan( 1 e −− 2 sin E s ) / 6)计算升交角距及轨道摄动改正项： 0u 升交角距： u 0 fω= + 0 s 摄动改正项：

δ u δ r δ i = = = c us c rs c is u sin 2 u sin 2 u sin 2 0 0 0 c u cos 2 + uc c u cos 2 + rc c u cos 2 + ic 0 0 0 （7） 7)计算经过摄动改正的升交角距u 、卫星到地心距离 r 、轨道倾角i u u δ = + u 0 E e r a (1 cos − = s s s i t i i t ( δ = + + − i e 0 0 ) ) δ + （8） r 8)计算卫星轨道平面坐标系中的坐标：卫星在轨道平面坐标系中的坐标为 r = r = x y cos sin u u （9） 9)计算观测时刻升交点经度：升交点经度λ为该时刻升交点赤经 Ω 与格林尼治恒星时 GAST 之差，即 λ= Ω − GAST （10）观测时刻的升交点赤经 Ω 为参考历元的升交点赤经 0et 0eΩ 加上观测时刻与参考历元之间的升交点的赤经变化，即 Ω = Ω + Ω − t ( 0 e t 0 )e （11）另外，卫星电文中提供了一周开始时刻（星期六子夜）以秒计算的格林尼治恒星时 GATS 。由于地球的自转作用，GAST 也不断增加。增加量与地球自 )t 0( 转速率有关 =7.29211567× 510 − rad s / 。所以，观测时刻 GAST 用下式计算： eW eW GAST=GAST )t +0( (eW t t− 0 ) （12）考虑到（11）式和(12)式，则 λ= Ω + Ω − ( t 0 e t 0 e ) GAST( − t W t ( 0 − ) e − t 0) (13) 因为 Ω = Ω − 0 e 0 t GAST( ) 0 λ= Ω + Ω − ( t 0 t 0 e ) − W t ( e − t 0) 考虑到和都是从开始起算，即＝0，则(13)式为 t 0et 0t 0t

λ= Ω + Ω − 0 ( ) W t ( e − t 0 e ) − W t e 0e （14） 10)计算卫星在地心坐标系中空间直角坐标： X ⎡ ⎢ Y ⎢ Z ⎢ ⎣ ⎤ ⎥ ⎥ ⎥ ⎦ = ⎡ ⎢ ⎢ ⎢ ⎣ λ − λ cos sin 0 i sin cos λ i cos cos − λ i sin i sin sin λ cos sin λ i cos i 0 X ⎡ ⎤ ⎢ ⎥ Y ⎢ ⎥ 0 ⎢ Z ⎥ ⎦ ⎣ 0 （15） ⎤ ⎥ ⎥ ⎥ ⎦ 11)如果考虑极移影响，可求在协议地球坐标系中的空间直角坐标： X ⎡ ⎢ Y ⎢ Z ⎢ ⎣ ⎤ ⎥ ⎥ ⎥ ⎦ CTS x 1 ⎡ p ⎢ y 0 = − ⎢⎥ ⎢ x 1 − ⎣ 0 1 y p p ⎤ X ⎡ ⎥ ⎢ Y ⎢ ⎥ ⎢ Z ⎣ ⎦ p ⎤ ⎥ ⎥ ⎥ ⎦ （16） 3 GPS 单点定位数学模型由于接收机测量的是伪距，在观测值中存在着接收机钟差，加之测量点的三维坐标为待求值，一共有 4 个未知数。要求解出这 4 个未知数，必须有 4 个方程式。为此，要实现单点绝对定位必须同时观测 4 颗卫星，才能组成定位的基本方程[4]。设ρ为伪距观测量，R 为接收机到卫星的真距离，τ为接收机钟差，则观测方程为 ρ = + × τ R c = ( X s − X 2 ) p + Y ( s − Y p 2 ) + ( Z − Z p s 2 ) + × （17） c τ 式中，假定伪距观测量ρ已经过星历中的对流层和电离层改正；( X Y Z 为卫 ) , , s s s 星的瞬时地心坐标，可由卫星星历电文中求出；( 是待求量。 X Y Z 为接收机的地心坐标， , , p p p ) 为了求解方便和数据处理的需要，将式（17）进行微分，作线性化处理，并将接收机的概略坐标 0 p ( X , Y , Z 作为初始值代入，得到 p ) 0 p 0 X s d = ρ X − R 0 p 0 X d + p 0 dY Z ++ s Y Y − s R 0 Z − R 0 p 0 t dZ d （18）式中， ddt c τ= 为接收机钟差对应的空间距离，

R 0 = ( X s − X 2 ) + Y Y ( − s p 0 2 ) + ( Z s − Z 2 0) p p 0 从式（18）中看出，三个坐标分量的系数是接收机到卫星的单位矢径分别向三个坐标轴投影的方向余弦。采用符号 l = X s X p − R m = Y Y − s R p n = Z s Z p − R （19）规定上标为卫星号，下标i 为测站号，则组成伪距定位的基本方程 d 1 ρ i d 2 ρ i d 3 ρ i d 4 ρ i ⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎡ ⎢ ⎢= ⎢ ⎢ ⎣ l m n 1 1 i i l m n 2 1 i i l m n 3 1 i i l m n 4 1 i i 1 i 1 i 1 i 1 i 1 ⎡ − ⎤ ⎢ ⎥− 1 ⎢ ⎥ ⎢ ⎥− 1 ⎢ ⎥ 1 − ⎦ ⎣ i dX dY i dZ t d i （20） ⎤ ⎥ ⎥ ⎥ ⎥ ⎦ 采用矩阵表示 l i A i X i 则式（20）变为 = ⎡ = ⎣ ⎡ ⎢ ⎢ ⎢ ⎢ ⎣ [ = d 4 ρ ρ ρ ρ i d d d 2 i 3 i 1 i T ⎤ ⎦ 观测量 l m n 1 1 i i l m n 2 1 i i l m n 3 1 i i l m n 4 1 i i 1 i 1 i 1 i 1 i dX dY dZ i i 1 − ⎤ ⎥− 1 ⎥ ⎥− 1 ⎥ 1 − ⎦ ] d T t i 状态矩阵未知数 A X l− = （21） i 0 i i 对式（21）求解，便得到接收机地心坐标的唯一解 X i A l−= 1 i i （22）在计算过程中，下列几个问题必须注意[11]：

（1）卫星之间的钟差是利用导航电文中给出的钟差改正数统一到 UTC 时间。这里，考虑的钟差是指卫星与接收机之间的钟差。（2）在计算中采用了接收机的概略坐标，第一次计算出的结果是不精确的。因此，必须反复迭代计算，直到满足规定的限差为止。（3）在一般导航型接收机中，都是采用这一数学模型计算位置的。现有的接收机都能同时跟踪四个以上卫星，但在计算中仍然利用四个卫星，不过是结果挑选的四个卫星。为此，按卫星的星座分布分成若干组，计算其 PDOP，最后选择和利用一组其 PDOP 为最小的卫星作为计算数据，以得到最高的定位精度。在测地型接收机和高质量的导航接收机中，都具有 8 个以上的通道，能同时跟踪 7 颗以上的卫星。为了提高定位精度，在计算位置过程中，利用了所有的卫星观测值。在这样情况下，出现了多余观测，观测值的个数超过了未知数的个数，使得式（21）的右端不等于零 A X l υ− = （23） i i i i 式中， Tυ υ υ υ 3 = ( , , 1 2 , T ) 为残差向量。根据最小二乘法的原理，最后得到接收机的位置解为其精度为 iX = ( A A A l T T ) − 1 （24） D m Q m A A 1− ) = = T 2 0 ( 2 x 0 x （25）式中，为伪距测量中误差， 0m xQ 为权系数阵。这种多余观测的优点在于消除了卫星定位的系统误差。过去，我们经常发现在仅用 4 颗卫星的差分定位中，当中间更换卫星时，位置会出现较大的偏移，等过了数秒后又逐渐回到原位。定位精度越高，这一现象越明显，当应用 4 颗以上的卫星定位时，这一现象就不存在了。 4 程序设计用 C++编写了几个小程序对 GPS 观测数据进行处理，包括时间转换程序、利用广播星历计算卫星坐标程序和地面点近似坐标计算程序，程序比较简单，使

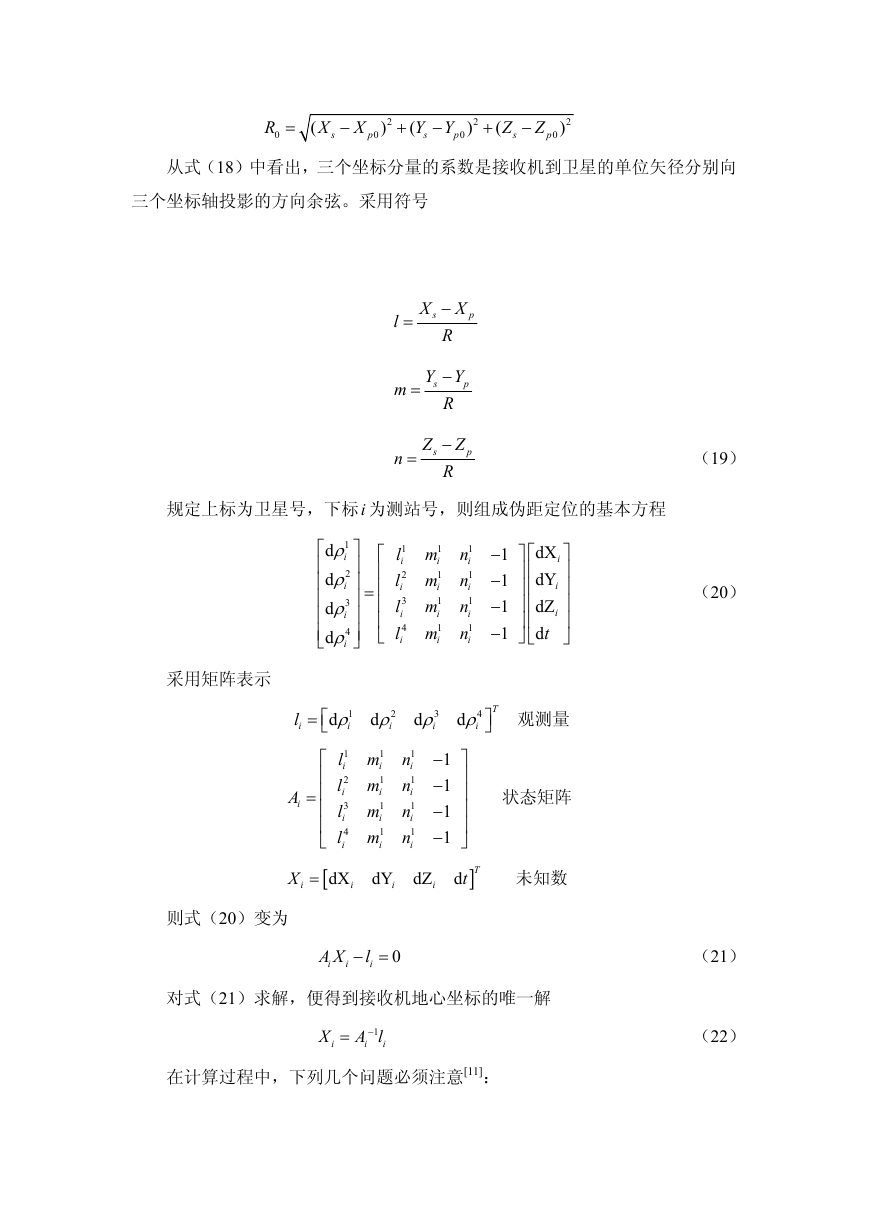
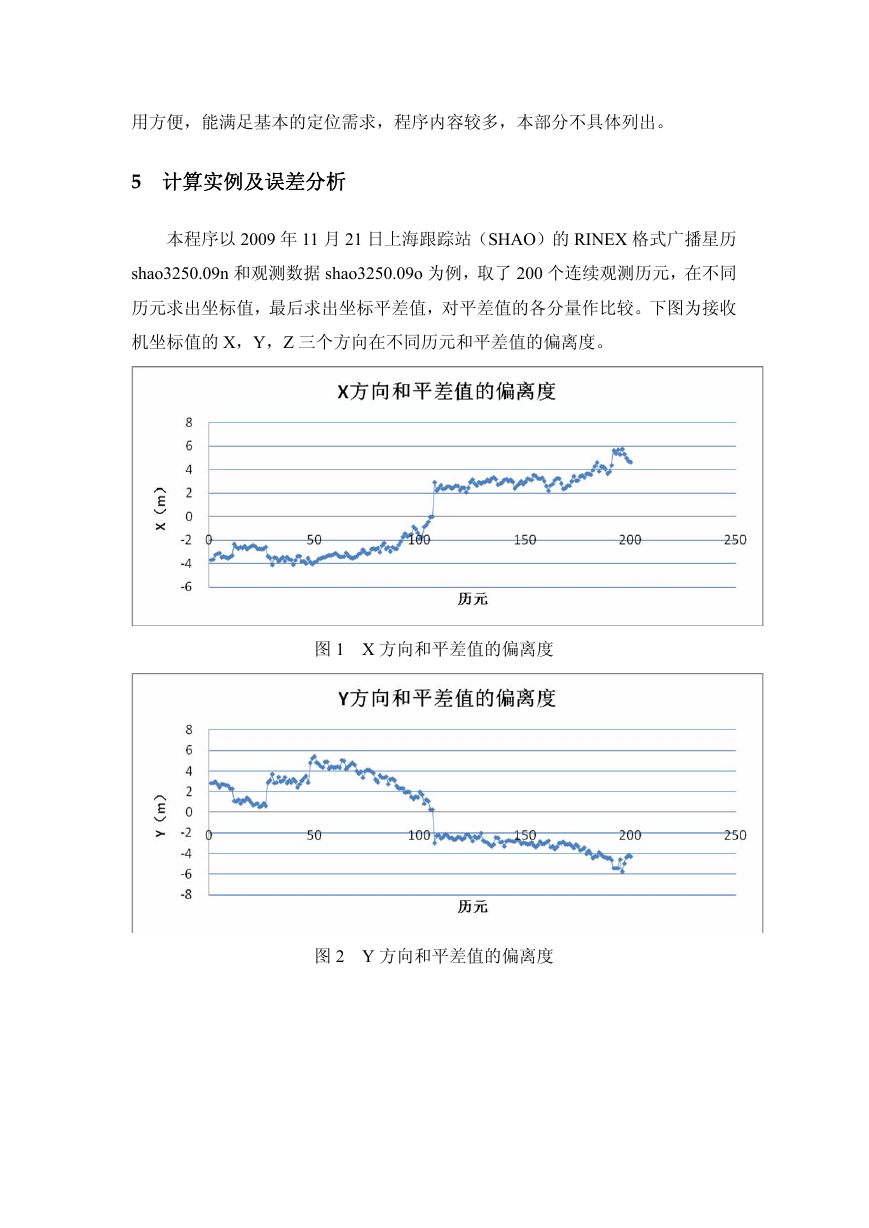
用方便，能满足基本的定位需求，程序内容较多，本部分不具体列出。 5 计算实例及误差分析本程序以 2009 年 11 月 21 日上海跟踪站（SHAO）的 RINEX 格式广播星历 shao3250.09n 和观测数据 shao3250.09o 为例，取了 200 个连续观测历元，在不同历元求出坐标值，最后求出坐标平差值，对平差值的各分量作比较。下图为接收机坐标值的 X，Y，Z 三个方向在不同历元和平差值的偏离度。图 1 X 方向和平差值的偏离度图 2 Y 方向和平差值的偏离度

资料库

写给新手程序员的一封信.pdf

相关推荐

课程资源

热门标签

最新资料