第1页 / 共52页
第2页 / 共52页
第3页 / 共52页
第4页 / 共52页
第5页 / 共52页
第6页 / 共52页
第7页 / 共52页
第8页 / 共52页
二机五节点的潮流程序.doc
摘 要
ABSTRACT
内蒙古科技大学课程设计任务书
第一章电力系统潮流计算简述
1.1 潮流计算简介
电力系统潮流计算是研究电力系统稳态运行情况的一种计算，它根据给定的运行条件及系统接线情况确定整个电力
电力系统潮流计算也分为离线计算和在线计算两种，前者主要用于系统规划设计和安排系统的运行方式，后者则用
对潮流计算的要求可以归纳为下面几点：
（1）计算方法的可靠性或收敛性；
（2）对计算机内存量的要求；
（3）计算速度；
（4）计算的方便性和灵活性。
电力系统潮流计算问题在数学上是一组多元非线性方程式求解问题，其解法都离不开迭代。因此，对潮流计算
1.2潮流计算的意义及发展史
第二章 潮流计算的数学模型
2.1 导纳矩阵的原理及计算方法
2.1.1自导纳和互导纳的确定方法
电力网络的节点电压方程：
为节点注入电流列向量，注入电流有正有负，注入网
为节点电压列向量，由于节点电压是对称于参考节点
节电导纳矩阵的节点电压方程：
展开为 ： (2
是一个n*n阶节点导纳矩阵，其阶数就等于网络中
(2-3)
节点i的自导纳数值上就等于与节点直接连接的所有
节点导纳矩阵的非对角元素 (j=1，2，
此可得互导纳数值上就等于在节点i施加单位电压，
节点j，i之间的互导纳数值上就等于连接节点j，
零元素相对愈来愈少，节点导纳矩阵的稀疏度，即零元素数与总元素的比值就愈来愈高。
2.2 潮流计算的基本方程
(a)潮流计算用的电网结构图
(b)在潮流问题中，任何复杂的电力系统都可以归纳为以下元件（参数）组成。
（1）发电机（注入电流或功率）
（2）负荷（注入负的电流或功率）
（3）输电线支路（电阻，电抗）
（4）变压器支路（电阻，电抗，变比）
（5）母线上的对地支路（阻抗和导纳）
（6）线路上的对地支路（一般为线路充电点容导纳）
集中了以上各类型的元件的简单网络如图(a).
采用导纳矩阵时，节点注入电流和节点电压构成以下线性方程组
其中
可展开如下形式 (2-6)
由于实际电网中测量的节点注入量一般不是电流而是功率，因此必须将式中的注入电流用节点注入功率来表示。
节点功率与节点电流之间的关系为
式中，
因此用导纳矩阵时，PQ节点可以表示为
把这个关系代入式中 ，得
（2-8）
式（3-4 ）就是电力系统潮流计算的数学模型-----潮流方程。它具有如下特点：
（1）它是一组代数方程，因而表征的是电力系统的稳定运行特性。
（2）它是一组非线性方程，因而只能用迭代方法求其数值解。
（3）由于方程中的电压和导纳既可以表为直角坐标，又可表为极坐标，因而潮流方程有多种表达形式---极坐
a。取 ，
(2-9)
b。 取 ，
(2-10)
c。取，
(2-11)
（4）它是一组n个复数方程，因而实数方程数为2n个但方程中共含4n个变量：P，Q，U和
2.3 电力系统节点分类
用一般的电路理论求解网络方程，目的是给出电压源(或电流源)研究网络内的电流(或电压)分布，作为基础的
①PQ节点
对这一类点，事先给定的是节点功率(P，Q)，待求的未知量是节点电压向量(U，
②PV节点
这类节点给出的参数是该节点的有功功率P及电压幅值U，待求量为该节点的无功功率Q及电压向量的相角
③平衡节点
在潮流计算中，这类节点一般只设一个。对该节点，给定其电压值，并在计算中取该节点电压向量的方向作为参考
关于平衡节点的选择，一般选择系统中担任调频调压的某一发电厂(或发电机)，有时也可能按其他原则选择，例
以上三类节点4个运行参数P、Q、U、中，已知量
2.4 潮流计算的约束条件
电力系统运行必须满足一定技术和经济上的要求。这些要求够成了潮流问题中某些变量的约束条件，常
1.节点电压应满足
(
2.从保证电能质量和供电安全的要求来看，电力系统的所有电气设备都必须运行在额定电压附近。PU节点电压
2.节点的有功功率和无功功率应满足
PQ节点的有功功率和无功功率，以及PU节点的有功功率，在给定是就必须满足上述条件，因此，对平衡节点的
4.节点之间电压的相位差应满足
(2-14)
为了保证系统运行的稳定性，要求某些输电线路两端的电压相位不超过一定的数值。这一约束的主要意义就在于
因此，潮流计算可以归结为求解一组非线性方程组，并使其解答满足一定的约束条件。常用的方法是迭代
第三章 牛顿－拉夫逊法概述
3.1 牛顿-拉夫逊法基本原理
电力系统潮流计算是电力系统分析中的一种最基本的计算，是对复杂电力系统正常和故障条件下稳态运行状态的计
牛顿--拉夫逊法(简称牛顿法)在数学上是求解非线性代数方程式的有效方法。其要点是把非线性方程式的求解
对于非线性代数方程组：
即
在待求量x的某一个初始估计值附近，将上式展开成
上式称之为牛顿法的修正方程式。由此可以求得第一次迭代的修正量
将和
上两式中：是函数
有上式可见，牛顿法的核心便是反复形式并求解修正方程式。牛顿法当初始估计值
牛顿潮流算法突出的优点是收敛速度快，若选择到一个较好的初值，算法将具有平方收敛特性，一般迭代4~5次
牛顿法的可靠收敛取决于有一个良好的启动初值。如果初值选择不当，算法有可能根本不收敛或收敛到一个无法运
这样一般能得到满意的结果。但若系统因无功紧张或其它原因导致电压质量很差或有重载线路而节点间角差很大时
3.2 牛顿---拉夫逊法潮流求解过程
以下讨论的是用直角坐标形式的牛顿—拉夫逊法潮流的求解过程。当采用直角坐标时，潮流问题的待求量为各节点
（3-7）
对PQ节点来说，是给定的，因而可以写出
（3-9）
求解过程大致可以分为以下步骤：
（1）形成节点导纳矩阵
（2）将各节点电压设初值U，
（3）将节点初值代入相关求式，求出修正方程式的常数项向量
（4）将节点电压初值代入求式，求出雅可比矩阵元素
（5）求解修正方程，求修正向量
（6）求取节点电压的新值
（7）检查是否收敛，如不收敛，则以各节点电压的新值作为初值自第3步重新开始进行狭义次迭代，否则转入下
（8）计算支路功率分布，PV节点无功功率和平衡节点柱入功率。
以直角坐标系形式表示
①.迭代推算式
采用直角坐标时,节点电压相量及复数导纳可表示为:
将以上二关系式代入上式中,展开并分开实部和虚部;假定系统中的第1,2,
⑴对于PQ节点
(3-11)
⑵对于PV节点
(3-12)
⑶对于平衡节点
平衡节点只设一个,电压为已知,不参见迭代,其电压为:
②.修正方程
选定电压初值及变量修正量符号之后代入式中,并将其按泰勒级数展开,略去
③.雅可比矩阵各元素的算式
式(3-7)中, 雅可比矩阵中的各元素可通过对式(3-11)和(3-12)进行偏导而求得.当
(3-15)
当时,雅可比矩阵中对角元素为:
(3-16)
3.3 牛顿—拉夫逊法的程序框图
第四章 关于电力系统潮流计算手工计算
4.1.节点导纳矩阵
4.2简化雅可比矩阵
4.3 修正、迭代
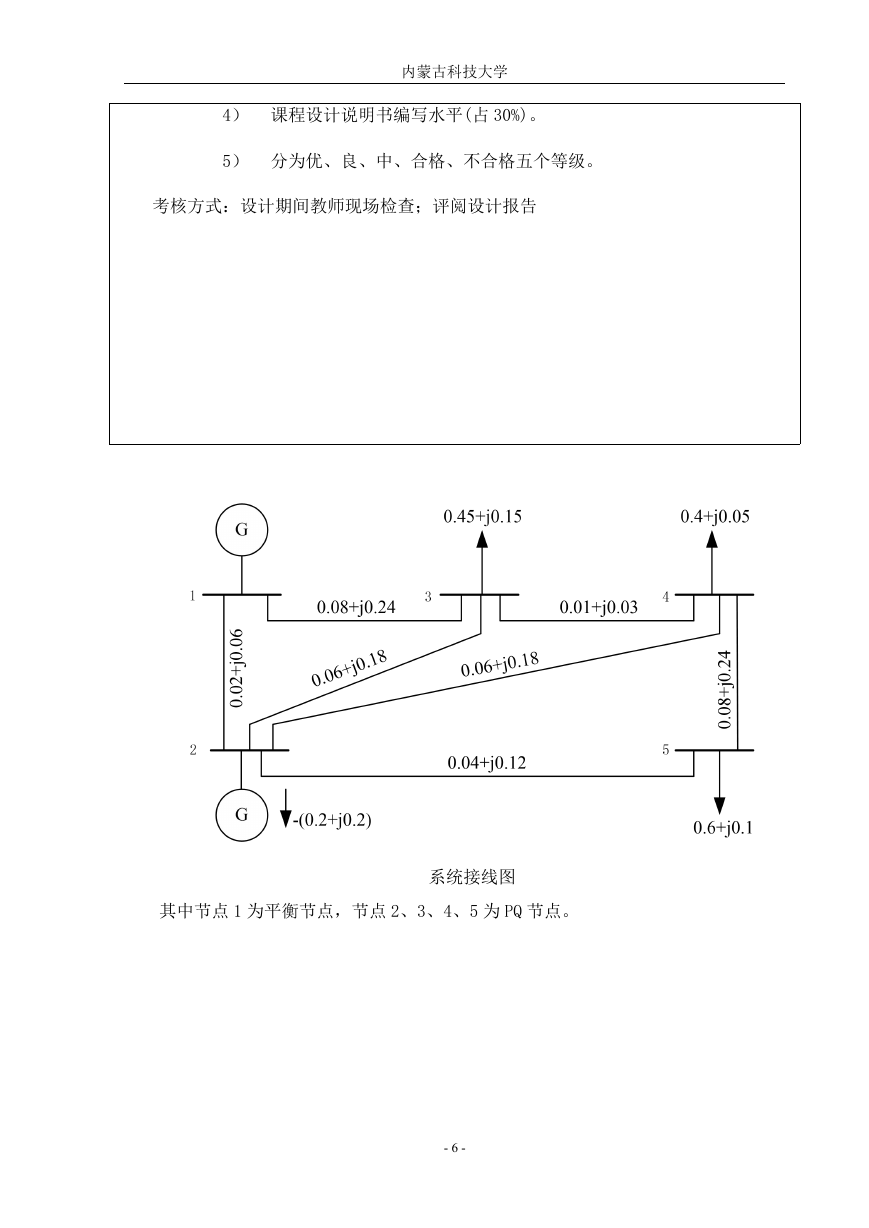
第五章 牛顿—拉夫逊法潮流具体计算
5.1 牛顿—拉夫逊直角坐标潮流计算Matlab程序及运行结果
5.1.1、Matlab程序
clc
clear
disp('节点总数为：');
N=5
disp('平衡节点为：');
1
disp('PQ节点为：');
JD=[2,3,4,5]
e=[1.06 1 1 1 1];
f=[0 0 0 0 0];
P1=0;
Q1=0;
P2=-0.2;
Q2=-0.2;
P3=0.45;
Q3=0.15;
P4=0.4;
Q4=0.05;
P5=0.6;
Q5=0.1;
G=[6.2500,-5.0000,-1.2500,0,0;-5.0000,10.8340,-1.6
B=[-18.75,15.0000,3.7500,0,0;15.0000,-32.5000,5.00
disp('节点电导矩阵G为:');
disp(G)
disp('节点电纳矩阵B为:');
disp(B)
k=0;
for v=1:7
I=[0,0;0,0;0,0;0,0;0,0];
for n=1:5
I(1,1)=I(1,1)+G(1,n)*e(n)-B(1,n)*f(n);
I(1,2)=I(1,2)+G(1,n)*f(n)+B(1,n)*e(n);
end
for n=1:5
I(2,1)=I(2,1)+G(2,n)*e(n)-B(2,n)*f(n);
I(2,2)=I(2,2)+G(2,n)*f(n)+B(2,n)*e(n);
end
for n=1:5
I(3,1)=I(3,1)+G(3,n)*e(n)-B(3,n)*f(n);
I(3,2)=I(3,2)+G(3,n)*f(n)+B(3,n)*e(n);
end
for n=1:5
I(4,1)=I(4,1)+G(4,n)*e(n)-B(4,n)*f(n);
I(4,2)=I(4,2)+G(4,n)*f(n)+B(4,n)*e(n);
end
for n=1:5
I(5,1)=I(5,1)+G(5,n)*e(n)-B(5,n)*f(n);
I(5,2)=I(5,2)+G(5,n)*f(n)+B(5,n)*e(n);
end
H=[];
N=[];
M=[];
L=[];
J=[];
P2=P2-e(2)*I(2,1)-f(2)*I(2,2); %有功功率的不平衡量
Q2=Q2-f(2)*I(2,1)+e(2)*I(2,2); %无功功率的不平衡量
P3=P3-e(3)*I(3,1)-f(3)*I(3,2);
Q3=Q3-f(3)*I(3,1)+e(3)*I(3,2);
P4=P4-e(4)*I(4,1)-f(4)*I(4,2);
Q4=Q4-f(4)*I(4,1)+e(4)*I(4,2);
P5=P5-e(5)*I(5,1)-f(5)*I(5,2);
Q5=Q5-f(5)*I(5,1)+e(5)*I(5,2);
for m=2:5
for n=2:5
if(m==n)
H(m,m)=-B(m,m)*e(m)+G(m,m)*f(m)+I(m,2)
N(m,m)=G(m,m)*e(m)+B(m,m)*f(m)+I(m,1);
M(m,m)=-G(m,m)*e(m)-B(m,m)*f(m)+I(m,1)
L(m,m)=-B(m,m)*e(m)+G(m,m)*f(m)-I(m,2)
else
H(m,n)=-B(m,n)*e(m)+G(m,n)*f(m);
N(m,n)=G(m,n)*e(m)+B(m,n)*f(m);
M(m,n)=-N(m,n);
L(m,n)=H(m,n);
end
end
end
J=[H(2,2),N(2,2),H(2,3),N(2,3),H(2,4),N(2,4),H(2,5
disp('雅克比矩阵J:');
disp(J);
A=[];
C=[P2;Q2;P3;Q3;P4;Q4;P5;Q5]
A=J\C;%解修正方程式
disp('第M次修正方程的解A:');
disp(A);
f(2)=f(2) +A(1,1);
e(2)=e(2) +A(2,1); %计算新值
f(3)=f(3) +A(3,1);
e(3)=e(3) +A(4,1);
f(4)=f(4) +A(5,1);
e(4)=e(4) +A(6,1);
f(5)=f(5) +A(7,1);
e(5)=e(5) +A(8,1);
disp('各点的电压实部e(单位:V)为(节点号从小到大排列):');
disp(e)
disp('各点的电压虚部f单位:V)为(节点号从小到大排列):');
disp(f);
u=e+f*i;
disp('节点电压的第C(k)次近似值:');
disp(u);
k=k+1;
disp('迭代次数:');
disp(k);
end
for m=1:5
I(m)=(G(1,m)+B(1,m)*i) *u(m);
end
disp('平衡节点的功率');
S1=u(1)*sum(conj(I))%计算平衡节点的功率
for m=1:5
for n=1:5
S(m,n)=u(m)*(conj(u(m))-conj(u(n)))*conj(-(
end
end
disp('各支路功率');disp(S) %结束
5.1.2、Matlab程序运行结果
节点总数为：
N =
5
平衡节点为：
ans =
1
PQ节点为：
JD =
2 3 4 5
节点电导矩阵G为:
6.2500 -5.0000 -1.2500 0 0
-5.0000 10.8340 -1.6670 -1.6670 -2.5000
-1.2500 -1.6670 12.9170 -10.0000 0
0 -1.6670 -10.0000 12.9170 -1.2500
0 -2.5000 0 -1.2500 3.7500
节点电纳矩阵B为:
-18.7500 15.0000 3.7500 0 0
15.0000 -32.5000 5.0000 5.0000 7.5000
3.7500 5.0000 -38.7500 30.0000 0
0 5.0000 30.0000 -38.7500 3.7500
0 7.5000 0 3.7500 -11.2500
雅克比矩阵J:
33.4000 10.5340 -5.0000 -1.6670 -5.0000
-11.1340 31.6000 1.6670 -5.0000 1.6670
-5.0000 -1.6670 38.9750 12.8420 -30.0000
1.6670 -5.0000 -12.9920 38.5250 10.0000
-5.0000 -1.6670 -30.0000 -10.0000 38.7500
1.6670 -5.0000 10.0000 -30.0000 -12.9170
-7.5000 -2.5000 0 0 -3.7500
2.5000 -7.5000 0 0 1.2500
C =
0.1000
0.7000
0.5250
0.3750
0.4000
0.0500
0.6000
0.1000
第M次修正方程的解A:
0.0473
0.0847
0.0863
0.1123
0.0922
0.1136
0.1076
0.1183
各点的电压实部e(单位:V)为(节点号从小到大排列):
1.0600 1.0847 1.1123 1.1136 1.1183
各点的电压虚部f单位:V)为(节点号从小到大排列):
0 0.0473 0.0863 0.0922 0.1076
节点电压的第C(k)次近似值:
1.0600 1.0847 + 0.0473i 1.1123 +
迭代次数:
1
雅克比矩阵J:
35.8747 9.9974 -5.5023 -1.5717 -5.5023
-10.4317 35.6555 1.5717 -5.5023 1.5717
-5.7052 -1.4227 44.0333 11.4624 -34.2310
1.4227 -5.7052 -10.5844 44.3968 8.5339
-5.7215 -1.3952 -34.3289 -8.3688 44.2915
1.3952 -5.7215 8.3688 -34.3289 -10.4101
-8.6564 -1.9888 0 0 -4.3282
1.9888 -8.6564 0 0 0.9944
C =
0.3304
0.8291
0.0524
0.1350
-0.0408
-0.0426
-0.0602
-0.0764
第M次修正方程的解A:
0.0006
0.0426
-0.0023
0.0355
-0.0031
0.0350
-0.0053
0.0331
各点的电压实部e(单位:V)为(节点号从小到大排列):
1.0600 1.1273 1.1478 1.1486 1.1514
各点的电压虚部f单位:V)为(节点号从小到大排列):
0 0.0479 0.0840 0.0891 0.1023
节点电压的第C(k)次近似值:
1.0600 1.1273 + 0.0479i 1.1478 +
迭代次数:
2
雅克比矩阵J:
36.5102 10.7859 -5.7161 -1.6398 -5.7161
-10.5284 37.7985 1.6398 -5.7161 1.6398
-5.8791 -1.4933 45.2683 12.0512 -35.2747
1.4933 -5.8791 -11.0902 45.8582 8.9577
-5.8913 -1.4693 -35.3479 -8.8133 45.6420
1.4693 -5.8913 8.8133 -35.3479 -11.0364
-8.8914 -2.1111 0 0 -4.4457
2.1111 -8.8914 0 0 1.0555
C =
0.2161
0.0969
-0.4743
-0.2439
-0.4389
-0.0915
-0.6573
-0.1748
第M次修正方程的解A:
-0.0475
-0.0199
-0.0853
-0.0428
-0.0908
-0.0436
-0.1052
-0.0469
各点的电压实部e(单位:V)为(节点号从小到大排列):
1.0600 1.1073 1.1050 1.1049 1.1045
各点的电压虚部f单位:V)为(节点号从小到大排列):
0 0.0003 -0.0013 -0.0018 -0.0029
节点电压的第C(k)次近似值:
1.0600 1.1073 + 0.0003i 1.1050 -
迭代次数:
3
雅克比矩阵J:
35.2528 12.2858 -5.5373 -1.8443 -5.5373
-11.6866 36.7320 1.8443 -5.5373 1.8443
-5.5229 -1.8487 42.6422 14.3784 -33.1375
1.8487 -5.5229 -14.2717 42.9630 11.0901
-5.5217 -1.8507 -33.1299 -11.1022 42.7999
1.8507 -5.5217 11.1022 -33.1299 -14.3648
-8.2764 -2.7827 0 0 -4.1382
2.7827 -8.2764 0 0 1.3913
C =
-0.1154
-0.7223
-0.5335
-0.4211
-0.4122
-0.0837
-0.6177
-0.1596
第M次修正方程的解A:
-0.0480
-0.0757
-0.0836
-0.1040
-0.0889
-0.1059
-0.1025
-0.1128
各点的电压实部e(单位:V)为(节点号从小到大排列):
1.0600 1.0317 1.0010 0.9990 0.9917
各点的电压虚部f单位:V)为(节点号从小到大排列):
0 -0.0476 -0.0849 -0.0907 -0.1054
节点电压的第C(k)次近似值:
1.0600 1.0317 - 0.0476i 1.0010 -
迭代次数:
4
雅克比矩阵J:
32.8618 12.9089 -5.0789 -1.9580 -5.0789
-12.5417 33.1637 1.9580 -5.0789 1.9580
-4.8637 -2.0933 37.8960 15.7849 -29.1823
2.0933 -4.8637 -16.6571 37.4917 12.5579
-4.8439 -2.1187 -29.0634 -12.7105 37.6263
2.1187 -4.8439 12.7105 -29.0634 -16.8168
-7.1742 -3.2695 0 0 -3.5871
3.2695 -7.1742 0 0 1.6347
C =
-0.3120
-0.8692
-0.0798
-0.2558
-0.0060
-0.0339
-0.0082
-0.0593
第M次修正方程的解A:
0.0002
-0.0651
-0.0007
-0.0714
-0.0010
-0.0721
-0.0017
-0.0749
各点的电压实部e(单位:V)为(节点号从小到大排列):
1.0600 0.9666 0.9297 0.9269 0.9168
各点的电压虚部f单位:V)为(节点号从小到大排列):
0 -0.0475 -0.0856 -0.0917 -0.1071
节点电压的第C(k)次近似值:
1.0600 0.9666 - 0.0475i 0.9297 -
迭代次数:
5
雅克比矩阵J:
31.5935 11.9468 -4.7538 -1.8487 -4.7538
-12.0832 30.2060 1.8487 -4.7538 1.8487
-4.5058 -1.9776 35.3997 14.8011 -27.0348
1.9776 -4.5058 -15.8476 34.4401 11.8638
-4.4815 -2.0036 -26.8889 -12.0200 34.8609
2.0036 -4.4815 12.0200 -26.8889 -15.9557
-6.6084 -3.0953 0 0 -3.3042
3.0953 -6.6084 0 0 1.5477
C =
-0.2131
-0.2019
0.4477
0.1455
0.4040
0.0467
0.6063
0.0943
第M次修正方程的解A:
0.0474
0.0385
0.0859
0.0782
0.0923
0.0814
0.1081
0.0930
各点的电压实部e(单位:V)为(节点号从小到大排列):
1.0600 1.0051 1.0079 1.0083 1.0098
各点的电压虚部f单位:V)为(节点号从小到大排列):
1.0e-003 *
0 -0.0853 0.3415 0.5798 0.9611
节点电压的第C(k)次近似值:
1.0600 1.0051 - 0.0001i 1.0079 +
迭代次数:
6
雅克比矩阵J:
33.5488 10.5814 -5.0254 -1.6759 -5.0254
-11.2029 31.7817 1.6759 -5.0254 1.6759
-5.0399 -1.6784 39.2521 12.9370 -30.2395
1.6784 -5.0399 -13.0738 38.8666 10.0684
-5.0424 -1.6779 -30.2541 -10.0654 39.0590
1.6779 -5.0424 10.0654 -30.2541 -12.9850
-7.5763 -2.5174 0 0 -3.7881
2.5174 -7.5763 0 0 1.2587
C =
0.0992
0.6861
0.5166
0.3398
0.3875
0.0273
0.5830
0.0557
第M次修正方程的解A:
0.0473
0.0775
0.0862
0.1015
0.0919
0.1023
0.1072
0.1051
各点的电压实部e(单位:V)为(节点号从小到大排列):
1.0600 1.0826 1.1093 1.1105 1.1149
各点的电压虚部f单位:V)为(节点号从小到大排列):
0 0.0472 0.0865 0.0925 0.1082
节点电压的第C(k)次近似值:
1.0600 1.0826 + 0.0472i 1.1093 +
迭代次数:
7
平衡节点的功率
S1 =
-1.2804 - 0.1912i 0.0000
各支路功率
0 -0.8712 - 0.1097i -0.4092 -
0.8849 + 0.1508i 0 -0.2575 -
0.4216 + 0.1187i 0.2613 + 0.0963i 0
0 0.2971 + 0.0963i 0.2157 -
0 0.5899 + 0.1581i 0
>>
5.1.3本程序的符号说明
本节主要介绍本设计任务书用到得指令。
（1）Clc，clear清屏，清除以前显示结果；
（2）disp 显示待输出的内容，如disp('节点总数为：')，显示：节点总数为：；
（3）while，end；，for，end；循环语句，用于要循环的地方；
（4）/ 正除；\ 反除；如DY=JJ\DW'
（5）sum 求和；
（6）conj 复数求共轭；
（7）' 矩阵的转置。
（8）% 注释
（9）： 自然数循环如1:5
（10）abs 取绝对值如abs(DY)
（11）max 取最大值如max(A)
（12）for- end 循环语句
（13）if-end语句
（14）if-else-end
总结及感想
参考文献及资料；
1、《电力系统稳态分析》，陈珩，中国电力出版社，2007，第三版
2、《Matlab在电气工程中的应用》，李维波，中国电力出版社，2007
3、《电力系统分析》，韩祯祥，浙江大学出版社，2005，第三版
4、《Matlab命令大全》姚东等，人民邮电出版社，2000，第一版
内蒙古科技大学
内蒙古科技大学
电力系统稳态分析课程设计
题
目：两机五节点网络潮流计算
—牛拉法
姓
学
学
专
班
名：朱润民
号：1167130230
院：信息工程学院
业：电气工程及其自动化
级：11 级电气 2 班
指导教师：刘景霞
1
内蒙古科技大学
目 录
目录 ............................................................................ - 1 -
摘 要 ......................................................................... - 2 -
ABSTRACT ........................................................................ - 3 -
内蒙古科技大学课程设计任务书 .................................................... - 3 -
第一章电力系统潮流计算简述 ...................................................... - 7 -
1.1 潮流计算简介 ............................................................ - 7 -
1.2 潮流计算的意义及发展史 ................................................... - 7 -
第二章 潮流计算的数学模型 ....................................................... - 9 -
2.1 导纳矩阵的原理及计算方法 ............................................... - 9 -
2.2 潮流计算的基本方程 .................................................... - 11 -
2.2 电力系统节点分类 ...................................................... - 11 -
2.4 潮流计算的约束条件 .................................................... - 11 -
第三章 牛顿－拉夫逊法概述 ...................................................... - 16 -
3.1 牛顿-拉夫逊法基本原理 ................................................. - 16 -
3.2 牛顿-拉夫逊法潮流求解过程 ............................................. - 16 -
3.3 牛顿—拉夫逊法的程序框图 .............................................. - 22 -
第四章 关于电力系统潮流计算手工计算 ........................................... - 23 -
4.1.节点导纳矩阵 ........................................................... - 23 -
4.2 简化雅可比矩阵 .......................................................... - 24 -
4.3 修正、迭代 ............................................................. - 24 -
第五章 牛顿—拉夫逊法潮流具体计算 ............................................. - 25 -
5.1 牛顿—拉夫逊直角坐标潮流计算 Matlab 程序及运行结果 ..................... - 25 -
5.1.1 Matlab 程序 ....................................................... - 25 -
5.1.2 Matlab 程序运行结果 ............................................... - 25 -
5.1.3 本程序的符号说明 .................................................. - 49 -
总结及感想 ..................................................................... - 50 -
参考文献及资料； ............................................................... - 51 -
1
内蒙古科技大学
摘 要
潮流计算的目的在于：确定电力系统的运行方式；检查系统中各元件是否过电压或
过载；为电力系统继电保护的整定提供依据；为电力系统的稳定计算提供初值，为电力
系统规划和经济运行提供分析基础。
牛顿迭代法（Newton's method）又称为牛顿-拉夫逊方法（Newton-Raphson method），
牛顿--拉夫逊法(简称牛顿法)在数学上是求解非线性代数方程式的有效方法。其要点是
把非线性方程式的求解过程变成反复地对相应的线性方程式进行求解的过程。MATLAB
是一种交互式、面向对象的程序设计语言，广泛应用于工业界与学术界，主要用于矩阵
运算．采用迭代法，通过建立矩阵的修正方程来依次迭代，逐步逼近真值来计算出电力
网的电压，功率分布。
采用迭代法，通过建立矩阵的修正方程来依次迭代，逐步逼近真值来计算出电力网
的电压，功率分布。
本文采用牛顿-拉夫逊法解算电力稳态潮流，用手算和计算机算法对其进行设计。
关键词： 电力系统潮流计算；牛顿—拉夫逊法潮流计算；程序；
- 2 -
内蒙古科技大学
ABSTRACT
The Power Flow computation's goal
lies in: Definite electrical power system's
movement way; In checkout system various parts whether overvoltage or overload; Provides
the basis for the electrical power system relay protection's installation; Provides the starting
value for electrical power system's stable computation, is the electrical power system plan and
the economical movement provides the analysis foundation.
The Newton iteration method (Newton's method) is called Newton - Rough to abdicate
the method (Newton - Rough method), Newton--Rough abdicates the law (i.e. Newton law) is
solves the misalignment algebraic equation in mathematics the efficacious device. Its main
point
is turns the misalignment equation solution process carries on repeatedly to the
corresponding linear equation the solution the process. MATLAB is one kind interactive,
the object-oriented programming language, widely applies in the industrial world and the
academic circle, mainly uses in the matrix operation. Uses the repetitive process, iterates in
turn through the establishment matrix's modified equation ,approaches the true value to
calculate electric power network's voltage gradually, the power distribution.
key word： Electrical power flow computation；Newton - Rough abdicates the law tidal
current computation； Procedure
- 3 -
内蒙古科技大学
内蒙古科技大学课程设计任务书
课程名称
电力系统稳态分析课程设计
设计题目
基于 Matlab 的两机五节点网络潮流仿真计算—牛拉法
指导教师
刘景霞
时间 1 周
一、教学要求
电力系统稳态分析课程设计以设计和优化电力系统的潮流分析为重点，提高学生
综合能力为目标，尽可能结合实际工程进行。设计内容的安排要充分考虑学校现有的设备，
设计时间及工程实际需要，并使学生初步学会运用所学知识解决工程中的实际问题。
二、设计资料及参数
（一）设计原始资料
1、待设计电气设备系统图
2、电力系统网络各元件参数
3、电力系统电气元件的使用规范
4、电力工程电气设计手册
（二）设计参考资料
1、《电力系统稳态分析》，陈珩，中国电力出版社，2007，第三版
2、《电力系统分析》，韩祯祥，浙江大学出版社，2005，第三版
3、《电力系统分析课程实际设计与综合实验》，祝书萍，中国电力出版社，2007，第
一版
- 4 -
内蒙古科技大学
三、设计要求及成果
1.根据给定的参数或工程具体要求，收集和查阅资料；学习相关软件（软件自选）。
2.在给定的电力网络上画出等值电路图。
3.运用计算机进行潮流计算。
4.编写设计说明书。
基本要求：
1.编写潮流计算程序；
2.在计算机上调试通过（？）；
3.运行程序并计算出正确结果（？）；
4.写出课程设计报告（包括以下内容）（1 份）
（1）程序框图；（2）源程序；（3）符号说明表；（4）算例及计算结果
5.编写计算说明书（1 份）。
四、进度安排
根据给定的参数或工程具体要求，收集和查阅资料（半天）
学习软件（MATLAB 或 C 语言等）（一天半）
编程计算复杂系统潮流计算（三天）
编写计算设计书（一天）
五、评分标准
课程设计成绩评定依据包括以下几点：
1） 工作态度（占 10%）；
2） 基本技能的掌握程度（占 20%）；
3） 程序编写是否合理是否有运行结果(40%)；
- 5 -
内蒙古科技大学
4） 课程设计说明书编写水平(占 30%)。
5） 分为优、良、中、合格、不合格五个等级。
考核方式：设计期间教师现场检查；评阅设计报告
其中节点 1 为平衡节点，节点 2、3、4、5 为 PQ 节点。
系统接线图
- 6 -
内蒙古科技大学
第一章电力系统潮流计算简述
1.1 潮流计算简介
电力系统潮流计算是研究电力系统稳态运行情况的一种计算，它根据给定的运行条
件及系统接线情况确定整个电力系统各部分的运行状态：各母线的电压，各元件中流过
的功率，系统的功率损耗等等。在电力系统规划的设计和现有电力系统运行方式的研究
中，都需要利用潮流计算来定量地分析比较供电方案或运行方式的合理性。可靠性和经
济性。此外，电力系统潮流计算也是计算系统动态稳定和静态稳定的基础。所以潮流计
算是研究电力系统的一种很重要和基础的计算。
电力系统潮流计算也分为离线计算和在线计算两种，前者主要用于系统规划设计和
安排系统的运行方式，后者则用于正在运行系统的经常监视及实时控制。
对潮流计算的要求可以归纳为下面几点：
（1）计算方法的可靠性或收敛性；
（2）对计算机内存量的要求；
（3）计算速度；
（4）计算的方便性和灵活性。
电力系统潮流计算问题在数学上是一组多元非线性方程式求解问题，其解法都离不
开迭代。因此，对潮流计算方法，首先要求它能可靠地收敛，并给出正确答案。由于电
力系统结构及参数的一些特点，并且随着电力系统不断扩大，潮流计算的方程式阶数也
越来越高，对这样的方程式并不是任何数学方法都能保证给出正确答案的。这种情况成
为促使电力系统计算人员不断寻求新的更可靠方法的重要因素。
1.2 潮流计算的意义及发展史
在电网规划阶段,通过潮流计算,合理规划电源容量及接入点,合理规划网架,选择无
功补偿方案,满足规划水平的大、小方式下潮流交换控制、调峰、调相、调压的要求。
在编制年运行方式时,在预计负荷增长及新设备投运基础上,选择典型方式进行潮流
- 7 -
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
