第 17 卷第 1 期 中国惯性技术学报 Vol.17 No.1 2009 年 2 月 Journal of Chinese Inertial Technology Feb. 2009 文章编号：1005-6734(2009)01-0085-04 贝叶斯神经网络建模预测方法及其应用 （1. 青岛科技大学 自动化与电子工程学院，青岛 266042；2. 上海交通大学 信息检测技术及仪器系，上海 200030） 樊春玲 1，孙四通 1，金志华 2 摘要：针对神经网络建模时，其模型的复杂性难以控制而且缺乏分析结果的工具，以及贝叶斯方法可以通过定 义一些超参数的模糊先验来控制模型参数复杂性，并且可对任何感兴趣的变量产生后验预测分布，使得置信区 间的计算成为可能。研究了贝叶斯神经网络的建模预测问题，通过融入模型参数的先验知识，在给定数据样本 及模型假设下进行后验概率的贝叶斯推理，使用马尔可夫链蒙特卡罗算法来优化模型控制参参数，实现了对神 经网络模型中不同部分复杂度的控制，获得了模型参数的后验分布及预测分布。通过动调陀螺仪漂移数据建模 应用分析结果证明此方法可以达到较好的建模预测效果。 关 键 词：贝叶斯神经网络；漂移建模；马尔可夫链蒙特卡罗（MCMC）；先验知识 中图分类号：U666.1 文献标志码：A Modeling & predictive method of Bayesian neural network FAN Chun-ling1, SUN Si-tong1, JIN Zhi-hua 2 (1. College of Automation and Electronic Engineering, Qingdao University of Science and Technology, Qingdao 266042, China; 2. Dept. of Information Measurement Technology and Instruments, Shanghai Jiao Tong Univ., Shanghai 200030, China) Abstract: With neural networks, the main difficulty in model building is controlling the complexity of the model and lack of tools for analyzing the results, such as confidence interval. However, Bayesian approach can handle such problems by defining vague priors for the hyperparameters that determine the model complexity. And the Bayesian analysis yields posterior predictive distributions for any variables of interest, making the computation of confidence intervals possible. Prior knowledge about the model parameters can be incorporated in Bayesian inference and combined with training data to control complexity of different parts of the model. Markov chain Monte Carlo method is applied to optimize the model control parameters and obtain the predictive distribution. The Bayesian neural network method is studied and used in the drift modeling for gyroscopes. Results show that the Bayesian neural network can produce better modeling and predictive performance. Key words: Bayesian neural network; drift modeling; Markov chain Monte Carlo (MCMC); prior knowledge 在贝叶斯数据分析中，所有未知变量的先验知识都是以概率分布的形式表示的。贝叶斯方法可以综合先验知识和观 测样本的数据信息，产生未知变量的后验分布。推理就是通过建立未知变量的后验条件概率分布来执行的，预测则是对 后验分布进行积分操作。当数据信息不充分的情况下，先验信息决定了最终的预测结果，随着数据信息的增加，先验信 息的影响也将逐渐减小[1]。 近年来，多层感知器（Multi-layer perception－MLP）神经网络在非线性建模、预测中的应用越来越普遍。对于神经 网络来说，它在建模上的一个主要困难是难以控制模型的复杂性。众所周知，模型最优自由度数目取决于训练样本数的 多少、样本的噪声程度以及所预测函数、方程的复杂性。对于标准神经网络来讲，确定正确的模型复杂性和设定理想的 网络复杂性的方法是非常粗糙的，且计算量非常庞大[2]。在贝叶斯方法中，神经网络的模型复杂度可以通过定义一些超参 数（hyperparameters）的模糊先验来控制模型参数复杂性的未知程度，再进一步通过对模型参数的分组，以及在各权组上 使用不同的公共超参数，允许模型在不同的部分有不同的复杂度，并且最终的模型是通过后验分布对整个模型的复杂度 收稿日期：2008-12-22；修回日期：2009-01-22 作者简介：樊春玲（1975—），女，副教授，从事陀螺仪可靠性及寿命预测、信息处理技术的研究。E-mail：peakfan@163.com 

86 中国惯性技术学报 第 17 卷 进行加权平均获得。标准神经网络中的另外一个主要问题是缺乏分析结果的工具，比如结论或结果的置信区间。而贝叶 斯分析对任何感兴趣的变量产生后验预测分布，使得置信区间的计算成为可能。因此，贝叶斯神经网络建模预测方法具 有较多优点，比如自动控制模型的复杂性，只用训练数据来选择正则化系数的值，而不需要运用不同的训练和验证数据； 对超参数可以运用先验信息和分等级模型（hierarchical model）；输出的结果是预测分布等等[3]。 陀螺仪作为惯性导航系统的测量基准元件，其漂移误差是决定惯性系统精度的主要因素之一。因此陀螺漂移数据的 处理和建模补偿工作显得非常重要。陀螺漂移中包含有规律的常值漂移和非确定性的随机漂移，前者可以在漂移测试的 基础上借助硬件或软件进行补偿；后者，尤其是动调陀螺仪的随机漂移是弱非平稳的有色噪声，通常采用自回归（AR） 模型进行建模。但是由于陀螺仪在启动过程中模型参数的不稳定性和逐次起动参数的不一致，很难建立准确、稳定的 AR 模型。文献[4]采用适当的递推算法，能够准确地估计出陀螺随机漂移中的随机游走项和发展趋势项。然而这些方法都是 采用 AR 模型建模，建模过程比较繁琐、费时。文献[5]论述了时间序列建模、BP 神经网络建模、Elman 动态递归神经网 络建模以及小波神经网络建模等主要的几种陀螺仪随机漂移建模方法，介绍了各种方法的特点及建模公式，但陀螺漂移 的建立还有很多工作要做。本文研究了贝叶斯神经网络建模方法，并且为了验证此方法的有效性和探讨新的动调陀螺仪 随机漂移建模方法，将其应用到动调陀螺仪的漂移建模中。 1 贝叶斯方法 贝叶斯方法的主要原理是在给定数据样本的情况下对模型中所有未知量建立后验概率分布。为了运用后验分布首先需 要对参数的先验分布进行明确定义。在给定样本数据 D 的情况下，根据式（1）贝叶斯法则模型 H 参数θ的后验分布为： p ( | θ D H , ) = p D ( | H p ( , ) | θ θ p D H | ( ) H ) （1） | , ) p D Hθ 是参数θ的似然函数； ( p p D H 是一个归一化常数。变量 H 定义了 式中， ( 关于选定模型的所有假设，比如选定模型为多层感知器（MLP）网络、特定的噪声模型等。所有的结果、推理都是基于 这些假设的，因此为了清楚起见将变量 H 写在方程之中。在这些定义下，归一化量 ( p D H 可以被直接理解为基于模 型假设 H 的条件下数据的边缘分布。它可以通过对所选择的假设 H 和先验 ( p Hθ 是参数θ的先验概率； ( Hθ 进行积分得到： ) ) ) ) | | | | 2 多层感知器（MLP）网络的贝叶斯学习 p D H ( | ) = ∫ θ p D H p ( ) | , θ ( | θ H )d θ （2） 在给定观测数据的情况下，贝叶斯建模的结果是感兴趣的未被观测变量的条件概率分布。在贝叶斯 MLP 网络中， 感兴趣的量是新输入值所对应的模型预测值，而对神经网络权值的后验分布不感兴趣。同样，在陀螺仪漂移建模预测时， 最终关心的不是神经网络权值的后验分布，而是根据此后验分布的模型预测值。 2.1 模 型 对于给定的训练数据 )} 测分布，可以依据模型的权值参数后验分布对模型预测进行积分： ),( {( ,( ), = n ( ) n ( ) (2) (2) 1 ( ) (1) , , , D x y x y x y ，在模型的新输入 newx 所对应的输出 newy 的后验预 p 式中，θ定义了所有的模型参数和先验结构的超参数； ( new p y ( new | x , D | ) x new new p y ( = ∫ Dθ 为权值参数后验分布。 | , | θ θ D p ) ( ) )d θ （3） p 对 于 测 量 的 概 率 模 型 ， ( D ( | θ ( ) θ θ p D ( ∝ p ) ) | p 的似然部分。在回归问题中带有加性噪声的概率模型为 θy x 包 含 了 所 选 择 的 逼 近 函 数 和 噪 声 模 型 。 它 也 定 义 了 后 验 概 率 项 ) , | 式中， ( ) f ⋅ 表示多层感知器 MLP 的函数方程 y = f x ( ; eθ )w + （4） f x ( ; θ = ) w 2 b + 2 w tan ( h b w x 1 + 1 ) （5） 、 、 、 ，分别对应于隐层的权值、偏差和输出层的权值、偏差。随机变量 e 是模 式中， wθ 定义了所有的参数 1 型残差，通常取为高斯噪声模型。对于多变量问题（多个输出）只需将式（4）的输出改为向量（这样输出有共同的残差 w b w b 1 2 2 模型）即可，或者通过完全不同的模型进行处理，或者是用具有一些公共部分的分等级模型（共同的隐层、不同的输出 权值和共同或分等级的噪声模型）来实现。 

第 1 期 樊春玲等：贝叶斯神经网络建模预测方法及其应用 87 2.2 预 测 当确定好模型和先验之后，和测量得到的样本数据信息进行组合，根据贝叶斯法则可以得到参数的后验分布， L 式中，θ代表模型中所有的参数和超参数； ( 所对应的模型预测值（加性零均值噪声模型）可以通过计算式（3）的后验预测分布的数学期望得到 | D L ) ~ ( ( ) θ （6） Dθ 为似然函数。根据模型预测均方误差的最优估计原则，一个新输入 p ( | θ ) D p ) | θ new ˆ y = E y [ new new | x , D ] = ∫ new f x ( , | θ θ p ) ( D )d θ （7） p 由于参数的后验分布 ( 参数逼近的方法或者借助数值积分近似法，如马尔可夫链蒙特卡罗法（MCMC）。 Dθ 带有多种模式，非常复杂，计算式（7）的积分是一个非常困难的任务。因此需要借助一些 ) | 2.3 马尔可夫链蒙特卡罗方法（MCMC） 由于在多层感知器 MLP 的贝叶斯学习中计算式（7）的积分是非常复杂、困难的，Neal 首先引入马尔可夫链蒙特卡 罗方法（Markov Chain Monte Carlo－MCMC）进行积分的计算[6]。MCMC 方法是一种新颖的非线性信号处理方法，越来 越受到人们的重视。在一种新框架下，它采用基于样本（Sampling-based）的方法能够进行贝叶斯检测。这类方法以寻找 最大后验概率解，即最优解为目的，它简单易实现，应用场合广泛，因此日益受到瞩目而成为研究的热点。 式（7）中的积分是函数 new f x θ 关于参数后验分布 ( p ( ) , Dθ 的期望，这个数学期望可以由 MCMC 方法来近似。 ) | 运用一组参数后验分布的采样值 ( )tθ 可得 new ˆ y n s + n 0 1 ≈ ∑ n s i n = 0 1 + new f x ( , t ( ) θ ) （8） 式中， 0n 为被舍弃的一些初始马尔可夫链以保证收敛性； sn 为来自平衡后验分布的权向量样本数。后验分布的采样是在 学习阶段进行的，因此其计算量可能非常庞大，但是运用相同的后验分布采样值和式（8），可以很快地计算出一个新输 入数据的预测输出值。 在 MCMC 中假设马尔可夫链满足遍历性，则由该链上的大量采样所达到的稳定分布就可代表式（6）的后验概率分 布。用结果马尔可夫链上的样本序列{ }tθ ，就可计算出式（8）。 3 应用与分析 由于陀螺仪漂移建模预测研究是动调陀螺仪性能的一个 重要组成部分，研究陀螺仪的漂移特性和漂移模型对陀螺仪 的可靠性非常重要。因此将动调陀螺仪的漂移数据用来进行 贝叶斯神经网络的建模预测有效性的研究。G01254-3 动调陀 螺仪实测的 100 天陀螺漂移数据如图 1 所示。 根据上述介绍的贝叶斯神经网络模型的理论，在进行贝 叶斯神经网络建模之前，首先需要确定网络的结构和网络权 值参数的先验分布。选择网络结构为一个输入变量、一个线 性输出变量和五个隐层节点，即 1-5-1 的神经网络模型。进行 训练的数据点为 ndata=20。由于漂移数据的先验知识不充分， 通常权值先验分布都采用最简单、最方便的高斯先验，因此 在此示例中，权值先验分布采用的是高斯分布。 确定好模型的结构和权值先验之后，就需要和测试数据 ) h / g e d ( / 移 漂 0.75 0.70 0.65 0.60 0.55 0.50 0.45 0.40 0.35 0 20 40 60 t/d 80 100 120 图 1 实测的 DTG 漂移 Fig.1 Real detected drift data 相结合，运用式（6）的贝叶斯法则，得到权值的后验分布；在后验分布的基础上，对一个新输入值，通过式（7）得 到其预测值；由于式（7）难以实现，通常采用 MCMC 来近似，权值的后验分布是通过 HMC 算法采样得到的一组收 敛的马尔可夫链。在进行采样之前，假定其权值衰减系数先验为 。接着，对网络 权值进行初始化，初始化值为对均值为 0，方差为 1 的高斯分布的随机采样值。然后，运用 HMC 采样算法进行权值后 验分布的采样，对后验权值的每个迭代过程进行 100 次采样，其中起始链中的前 200 个采样点被忽略，即 0 。 在采样过程中，当设定的阈值大于介于 0 和 1 之间的随机数，则接受新的状态。HMC 采样完成之后形成的数据链作为 网络的后验权值。 ；数据误差系数为 n = 200 0.01α= 100β= 

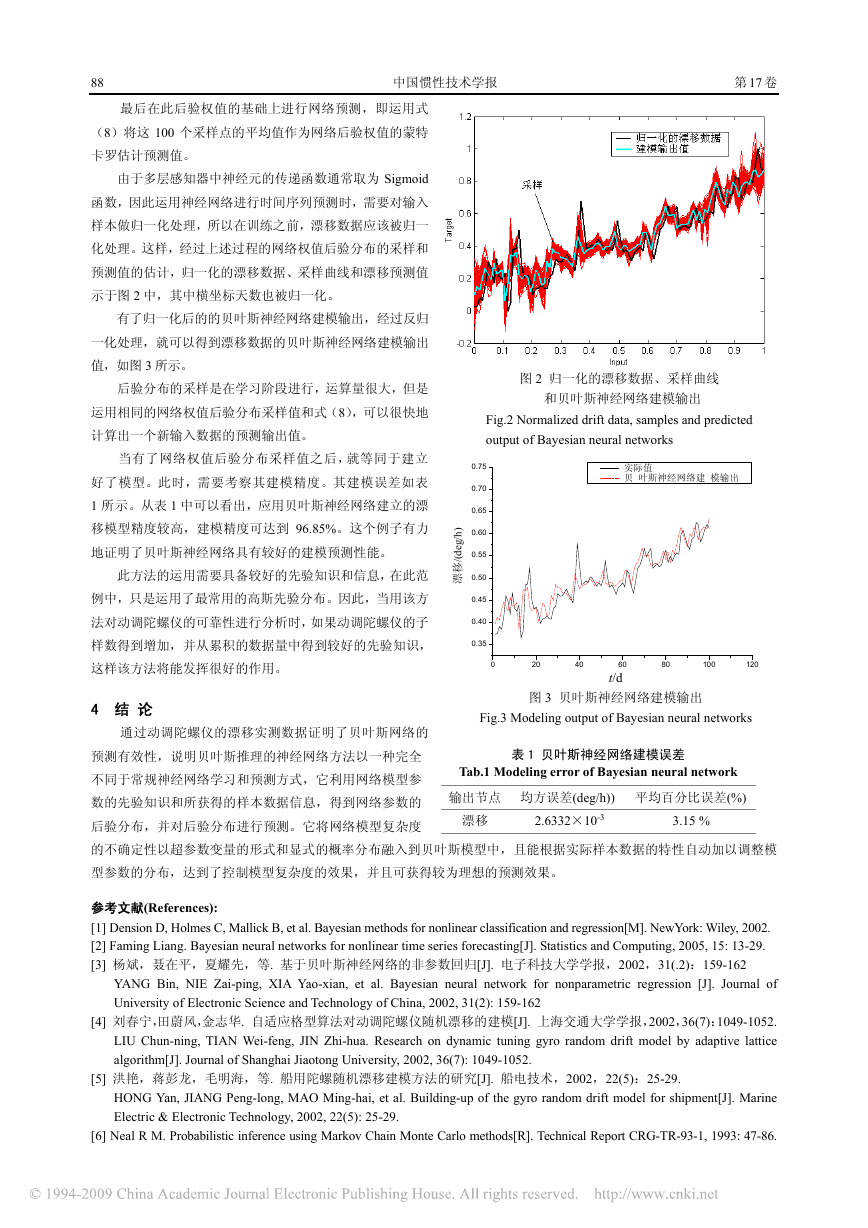
88 中国惯性技术学报 第 17 卷 最后在此后验权值的基础上进行网络预测，即运用式 （8）将这 100 个采样点的平均值作为网络后验权值的蒙特 卡罗估计预测值。 由于多层感知器中神经元的传递函数通常取为 Sigmoid 函数，因此运用神经网络进行时间序列预测时，需要对输入 样本做归一化处理，所以在训练之前，漂移数据应该被归一 化处理。这样，经过上述过程的网络权值后验分布的采样和 预测值的估计，归一化的漂移数据、采样曲线和漂移预测值 示于图 2 中，其中横坐标天数也被归一化。 有了归一化后的的贝叶斯神经网络建模输出，经过反归 一化处理，就可以得到漂移数据的贝叶斯神经网络建模输出 值，如图 3 所示。 后验分布的采样是在学习阶段进行，运算量很大，但是 运用相同的网络权值后验分布采样值和式（8），可以很快地 计算出一个新输入数据的预测输出值。 当有了网络权值后验分布采样值之后，就等同于建立 好了模型。此时，需要考察其建模精度。其建模误差如表 1 所示。从表 1 中可以看出，应用贝叶斯神经网络建立的漂 移模型精度较高，建模精度可达到 96.85%。这个例子有力 地证明了贝叶斯神经网络具有较好的建模预测性能。 此方法的运用需要具备较好的先验知识和信息，在此范 例中，只是运用了最常用的高斯先验分布。因此，当用该方 法对动调陀螺仪的可靠性进行分析时，如果动调陀螺仪的子 样数得到增加，并从累积的数据量中得到较好的先验知识， 这样该方法将能发挥很好的作用。 4 结 论 图 2 归一化的漂移数据、采样曲线 和贝叶斯神经网络建模输出 Fig.2 Normalized drift data, samples and predicted output of Bayesian neural networks 实际值 贝 叶斯神经网络建 模输出 ) h / g e d ( / 移 漂 0.75 0.70 0.65 0.60 0.55 0.50 0.45 0.40 0.35 0 20 40 60 t/d 80 100 120 图 3 贝叶斯神经网络建模输出 Fig.3 Modeling output of Bayesian neural networks 通过动调陀螺仪的漂移实测数据证明了贝叶斯网络的 预测有效性，说明贝叶斯推理的神经网络方法以一种完全 不同于常规神经网络学习和预测方式，它利用网络模型参 数的先验知识和所获得的样本数据信息，得到网络参数的 后验分布，并对后验分布进行预测。它将网络模型复杂度 表 1 贝叶斯神经网络建模误差 Tab.1 Modeling error of Bayesian neural network 输出节点 均方误差(deg/h)) 平均百分比误差(%) 漂移 2.6332×10-3 3.15 % 的不确定性以超参数变量的形式和显式的概率分布融入到贝叶斯模型中，且能根据实际样本数据的特性自动加以调整模 型参数的分布，达到了控制模型复杂度的效果，并且可获得较为理想的预测效果。 参考文献(References): [1] Dension D, Holmes C, Mallick B, et al. Bayesian methods for nonlinear classification and regression[M]. NewYork: Wiley, 2002. [2] Faming Liang. Bayesian neural networks for nonlinear time series forecasting[J]. Statistics and Computing, 2005, 15: 13-29. [3] 杨斌，聂在平，夏耀先，等. 基于贝叶斯神经网络的非参数回归[J]. 电子科技大学学报，2002，31(.2)：159-162 YANG Bin, NIE Zai-ping, XIA Yao-xian, et al. Bayesian neural network for nonparametric regression [J]. Journal of University of Electronic Science and Technology of China, 2002, 31(2): 159-162 [4] 刘春宁，田蔚风，金志华. 自适应格型算法对动调陀螺仪随机漂移的建模[J]. 上海交通大学学报，2002，36(7)：1049-1052. LIU Chun-ning, TIAN Wei-feng, JIN Zhi-hua. Research on dynamic tuning gyro random drift model by adaptive lattice algorithm[J]. Journal of Shanghai Jiaotong University, 2002, 36(7): 1049-1052. [5] 洪艳，蒋彭龙，毛明海，等. 船用陀螺随机漂移建模方法的研究[J]. 船电技术，2002，22(5)：25-29. HONG Yan, JIANG Peng-long, MAO Ming-hai, et al. Building-up of the gyro random drift model for shipment[J]. Marine Electric & Electronic Technology, 2002, 22(5): 25-29. [6] Neal R M. Probabilistic inference using Markov Chain Monte Carlo methods[R]. Technical Report CRG-TR-93-1, 1993: 47-86.