基于原-对偶内点法的电力市场实时电价计算.pdf-资料库

基于原-对偶内点法的电力市场实时电价计算 http://www.paper.edu.cn 张丽钦，袁越，钱科军河海大学电气工程学院，南京（210098） E-mail：zhangliqin711026@hhu.edu.cn 摘要：根据实时电价理论，结合实时电价与最优潮流之间存在的内在联系，即最优潮流中的拉格朗日乘子与实时电价中的有功无功电价有着相同的经济含义，建立以发电机燃料费用最小为目标函数，并考虑功率平衡约束及网络约束对电价的影响，利用最优潮流计算了电力市场下系统各节点的实时电价。考虑到原－对偶内点法最优潮流在每次迭代时都要重新计算修正方程系数矩阵及其因子表，占用了迭代计算的大部分时间，在很大程度上影响了计算速度，不利于实时电价的在线计算。本文将采用稀疏技术对修正方程系数矩阵中元素重新排列，大大减少注入元，提高计算速度。关键词：电力系统；电力市场；原－对偶内点法；实时电价 1. 引言中国的电力工业正在进行“厂网分开，竞价上网”的改革，目的是在发电领域逐步引入竞争机制，逐步形成开放发电侧的经营模式。电价是调节电力市场的杠杆，近几年来，电价问题成为一个许多专家研究的热点问题。由于实时电价能在给定时段向用户提供电能的边际成本，它能反映短期的电力生产成本和需求信息，从而指导用户合理用电、优化资源配制。实时电价理论的研究可以追溯到 70 年代末期。其早期的理论研究成果由 Schweppe 等人总结于文献[1]中。文献[2]研究了实时电价各组成部分的物理与经济意义。90 年代后，实时电价理论从两方面都得到了长足的发展：即模型本身的发展和计算方法的进步。模型的完善是人们长期以来对电力系统优化运行的理解逐步深入、经验逐步积累的自然结果，计算方法的进步则与最优潮流乃至优化数学本身的发展紧密相关。文献[3]应用修正的最优潮流研究了实时电价政策对用户的影响，这是最优潮流应用于实时电价的首次尝试。文献[4]进一步发展了这一模型，提出了利用最优潮流求解无功实时电价的方法，最重要的贡献是发现了最优潮流中对应于潮流平衡方程的拉格朗日乘子 λp，λq 与有功、无功负荷的实时电价具有相同的经济含义，从而说明了最优潮流是一种极具潜力的实时电价计算方法。但该模型的缺陷在于发电机节点的无功价格计算，在无功发电容量没有越限时，无功的价格为零，这显然不利于无功市场的形成。文献[5]提出了一种基于解耦最优潮流的有功、无功实时电价方法。本文根据实时电价理论，结合实时电价与最优潮流之间存在的内在联系，即最优潮流中的拉格朗日乘子与实时电价中的有功无功电价有着相同的经济含义，建立以发电机燃料费用最小为目标函数，并考虑功率平衡约束及网络约束对电价的影响，利用最优潮流计算了电力市场下系统各节点的实时电价。考虑到原－对偶内点法最优潮流在每次迭代时都要重新计算修正方程系数矩阵及其因子表，占用了迭代计算的大部分时间，在很大程度上影响了计算速度，不利于实时电价的在线计算。文中将采用稀疏技术对修正方程系数矩阵中元素重新排列，大大减少注入元，提高了计算速度。 2. 实时电价的概念 2.1 实时电价的提出电力是商品，商品交换靠的是价格，而价格应使供需双方都能接受才能成交，因此电价是电力市场的支点。现行的定价方式尽管考虑了不同的供电时段且具有不同的发电成本， - 1 -

http://www.paper.edu.cn 制订了时段电价和季节电价。但这种定价方式只反映供应侧成本，而将电力产品视为同一品质属性的商品，没有考虑用户特性[6]。 2.2 实时电价的作用实时电价充分利用电力市场供需状况对其的影响，自动反馈调节用户负荷，通过经济利益激励用户配合市场调度员共同实现电力负荷在一定时空的最佳分布, 从而实现电力商品的社会价值最优[7]。 2.3 实时电价的构成实时电价能反映短期的生产成本及用电量信息，能够指导用户优化用电。实时电价是在考虑运行和基本投资的情况下，在给定时段，如 0.5h 或更短时段向用户提供电能的边际成本。其数学表达式为[8]： ρ k = C ∂ W ∂ w d , k d , （1）式中：ρk,t－第 k 个用户在时段 t 的实时电价； Cw,d－供电系统为所有用户提供电量的总电量成本（即运行成本）；Ｗk,d－第 k 个用户在时段 t 的负荷。此数学表达式同时满足以下约束：（1）电量平衡约束，即发电量应为在时段 t 的负荷用电量与网络损耗之和；（2）发电功率约束，即负荷功率及损耗功率之和应小于系统总的可用发电容量；（3）线路功率约束，任一线路的潮流不能超过其极限值。 3. 实时电价计算数学模型 3.1 内点法应用于实时电价计算的可行性实时电价就是在考虑运行和基本投资的情况下，在给定时段向用户提供电能的边际成本。内点法最优潮流在计算实时电价方面具有很大的潜力，具体体现在：（1）内点法最优潮流本质上是拉格朗日（Lagrangian）函数、牛顿法和对数障碍函数三者的结合，因此不仅充分继承了牛顿法最优潮流的概念清晰、算法鲁棒性强、收敛速度快的优点，而且在处理不等式约束时将函数型不等式约束和变量型不等式约束一并处理，不需要额外的有效约束集确定程序，避免了牛顿法的缺陷。（2）内点法最优潮流中的对偶变量提供了丰富的经济信息，其值对应于相应约束的影子价格。（3）实时电价的模型中所需的数据都是内点法最优潮流中的各辅助变量，因此将内点法最优潮流转换为定价工具的工作量非常小。总的来说，最优潮流适合于计算实时电价，而内点法最优潮流与其他最优潮流算法相比，不仅在算法性能上更具优势，而且又能提供更丰富的经济信息。但是，实时电价的算法除了需要具备以上优点外，在计算速度上还需要具有绝对的优势来满足在线计算的要求。而内点法最优潮流在每次迭代时都要重新计算修正方程系数矩阵及其因子表，占用了迭代计算的大部分时间，在很大程度上影响了计算速度，不利于实时电价的在线计算。基于此，本文采用稀疏技术对修正方程系数矩阵中元素重新排列，大大减少了注入元，提高了计算速度。 3.2 目标函数设模型所描述的电力系统有 m 台发电机，n 个节点和 k 条线路。 - 2 -

本文采用发电费用作为目标函数。在电力市场中，除了有功费用外，无功费用也应被计及。本模型中的有功和无功生产费用均用二次曲线描述： http://www.paper.edu.cn 其中： f x min ( ) = f P ) ( gi pi f Q ) ( qi gi = = c P Pi gi c Q Qi gi 3.3 等式约束等式约束 g(X) = 0，即潮流方程： m i 2 ∑ 1 = + + 2 ( f P ( pi gi ) + f Q qi gi ( )) （2） b P Pi gi b Q Qi gi a+ Pi a+ Qi i ( i ( = = L 1, 1, L , , m ) m ) （3）（4） V G ij ( j V G ij ( j cos Bθ ij ij + sin θ ij ) 0 = （5） sin Bθ ij ij − cos θ ij ) 0 = （6） n ∑ j j 1 = i ≠ n ∑ j j 1 = i ≠ P gi − P V G V di i − − ii 2 i Q Q V B V i − − + gi di ii 2 i 3. 4 不等式约束不等式约束 h(X) = 0 包括：容量约束 P gi Q gi min min ≤ ≤ P gi Q gi ≤ ≤ P gi Q gi i max ( i max ( 1, = L 1, = L , , m ) m ) （7）（8）电压约束线路潮流约束 V i min ≤ V V i i ≤ i max ( 1, = L , m ) （9） − P ij max ≤ P ij ≤ P ij i max ( , j 1, = L , m ) （10）其中，X = (Pg, Qg, θ, V)T 为状态变量。 3. 5 实时电价计算公式引入松弛变量 l，u 将不等式约束变成等式约束，并引入对数障碍函数，并对等式约束引入拉格朗日乘子 z，w，得到增广的目标函数如下[9]： min L = m ∑ i 1 = ( f P ( pi gi ) + f Q qi gi ( )) − n ∑ i 1 = λ pi g pi − m ∑ i 1 = λ qi g qi − − − − m ∑ i 1 = k ∑ i 1 = n ∑ i 1 = w P gi pgi ( + u pgi − P gi max ) − m ∑ i 1 = z Q l − qgi ( gi − Q gi min ) − qgi z P l − pli ( li − P li min ) − pli k ∑ i 1 = w P u + ( pli li w V u + vi ( i − V i vi max ) − ( µ r ∑ i 1 = ln u i + r ∑ i 1 = n ∑ i 1 = − P li max ) − p li l ln ) i m ∑ i 1 = m ∑ i 1 = z ( P gi − l pgi − P gi pgi min ) w Q u qgi + ( gi − Q gi max ) qgi （11） z V l − vi vi ( i − V i min ) 其中，λ = ( λp, λq)T 为潮流等式约束的拉格朗日乘子。从经济意义上讲，各节点的有功（无功）实时电价（用 SP 表示）等于最优解处各节点的拉格朗日乘子的值，所以对实时电价的分解实际上就是对拉格朗日乘子进行分解： - 3 -

http://www.paper.edu.cn p SP i = q SP i = L ∂ P ∂ i L ∂ Q ∂ i = λ pi i ( = 1, L n , ) （12） = λ qi i ( = 1, L n , ) （13）设平衡节点编号为 s，Ploss，Qloss 分别为系统有功、无功网损，则对于系统整体，有：（14） = P P i s + P loss Q Q Q + = s i loss （15） i s ≠ ∑ ∑ i s ≠ 由（14）可以得到： P ∂ loss X ∂ = P i ∂ ∑ i s ≠ X ∂ + P ∂ s X ∂ = ∑ i s ≠ P ∂ loss P ∂ i P ∂ i X ∂ + ∑ i s ≠ P Q ∂ ∂ loss i Q X ∂ ∂ i （16）同理，有： ∑ i s ≠ Q ∂ loss P ∂ i P ∂ i X ∂ + ( ∑ i s ≠ Q ∂ loss Q ∂ i − 1) Q ∂ i X ∂ （17） = Q ∂ loss X ∂ 将上述两式写成矩阵形式： M P ∂ loss P ∂ i P ∂ loss Q ∂ i M ⎡ ⎢ ⎢ 1 ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ P ∂ s X ∂ − = J T ， Q ∂ s X ∂ = T J ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ M ⎡ ⎢ Q ∂⎢ loss P ∂ ⎢ i ⎢ Q ∂ ⎢ 1 loss Q ⎢ ∂ i ⎢ M ⎢ ⎣ − ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ i ，( = 1, L , n i ( ≠ s )) （18）由（11）可得： − = L ∂ X ∂ F ∂ X ∂ P F ∂ ∂ s P X ∂ ∂ s 将（18）代入（20）中，可得： = λ J ( ) ( T − 1 T J + + λ h T ∂ X ∂ Q F ∂ ∂ s Q X ∂ ∂ s ( z w + ) 0 = （19） ) + ( J T ) − 1 h T ∂ X ∂ ( z w ) + （20） p ( ) − = − = λ pi SP i (1 = − F ∂ P ∂ s P ∂ loss P ∂ i F ∂ P ∂ s Q F F ∂ ∂ ∂ loss P P Q ∂ ∂ ∂ i s s Q F ∂ ∂ loss P Q ∂ ∂ s i P F ∂ ∂ loss Q P ∂ ∂ s i P F ∂ ∂ loss Q P ∂ ∂ s 式（21）、（22）就是实时电价的计算公式。 P ∂ loss P ∂ i Q F ∂ ∂ loss Q Q ∂ ∂ i s Q F ∂ ∂ loss Q Q ∂ ∂ s F ∂ Q ∂ s (1 = − SP i λ qi + − = − = − + − ) ) ( ) q i i ( − h T ∂ P ∂ i h T ∂ P ∂ i h T ∂ Q ∂ i h T ∂ Q ∂ i ( − z w ) + z w ) + ( z w ) + （21） ( z w ) + （22） - 4 -

http://www.paper.edu.cn 4. 原-对偶内点法 4.1 概述自从1984年Karmarkar提出内点法以来，许多学者对该算法进行了广泛深入的研究。内点法本质上是拉格朗日函数、牛顿法和对数障碍函数法三者的结合，从初始内点出发，沿着最速下降方向，从可行域内部直接走向最优解。原-对偶内点法是在保持解的原始可行性和对偶可行性的同时, 沿一条原-对偶路径寻到最优解，并在此过程中能始终维持原始解和对偶解的可行性，在处理不等式约束以及迭代收敛方面显现出较明显的优势，该方法对初始点的选择不敏感[10]。对于常规非线性规划问题，其数学模型可以描述为[11]：目标函数： f x ( ) 0 g < h x = (22) ( ) 约束条件： g g x ( ) < 式中：x 为状态变量的集合， n x R∈ 。目标函数： ( ) h x , L ( ), 为 m 维列向量， 1 ； g 、 g 分别为不等式约束的上、下限，均为 r 维列向量。 g x L ( ) R→ ；等式约束 ( )h x ： n R ；不等式约束 ( )g x ： n R R→ 为 r 维列向量， h x [ ( ) = g x ( )]T , r f x ， nR = [ g x ( ), 1 h x m ( )]T 1 R→ m r 4.2 考虑稀疏技术的原－对偶内点法所谓引入稀疏排列技术[12]，就是将修正方程中的系数矩阵和修正量向量的元素进行交叉排列，使得系数矩阵具有和节点导纳矩阵类似的结构，这样就可根据节点导纳矩阵的结构形成修正方程系数矩阵，而且可以大大减少计算时的注入元数量。同时，对内点法最优潮流修正方程的排列结构改进之后，可以将 ∆l, ∆u, ∆z ∆w 的方程放在修正方程以外求解，使修正方程式系数矩阵仅由海森矩阵和雅克比矩阵构成，大大降低了系数矩阵的规模。 5. 基于原-对偶内点法的电力市场实时电价计算 5.1 计算流程基于原-对偶内点法的电力市场实时电价计算流程如下： - 5 -

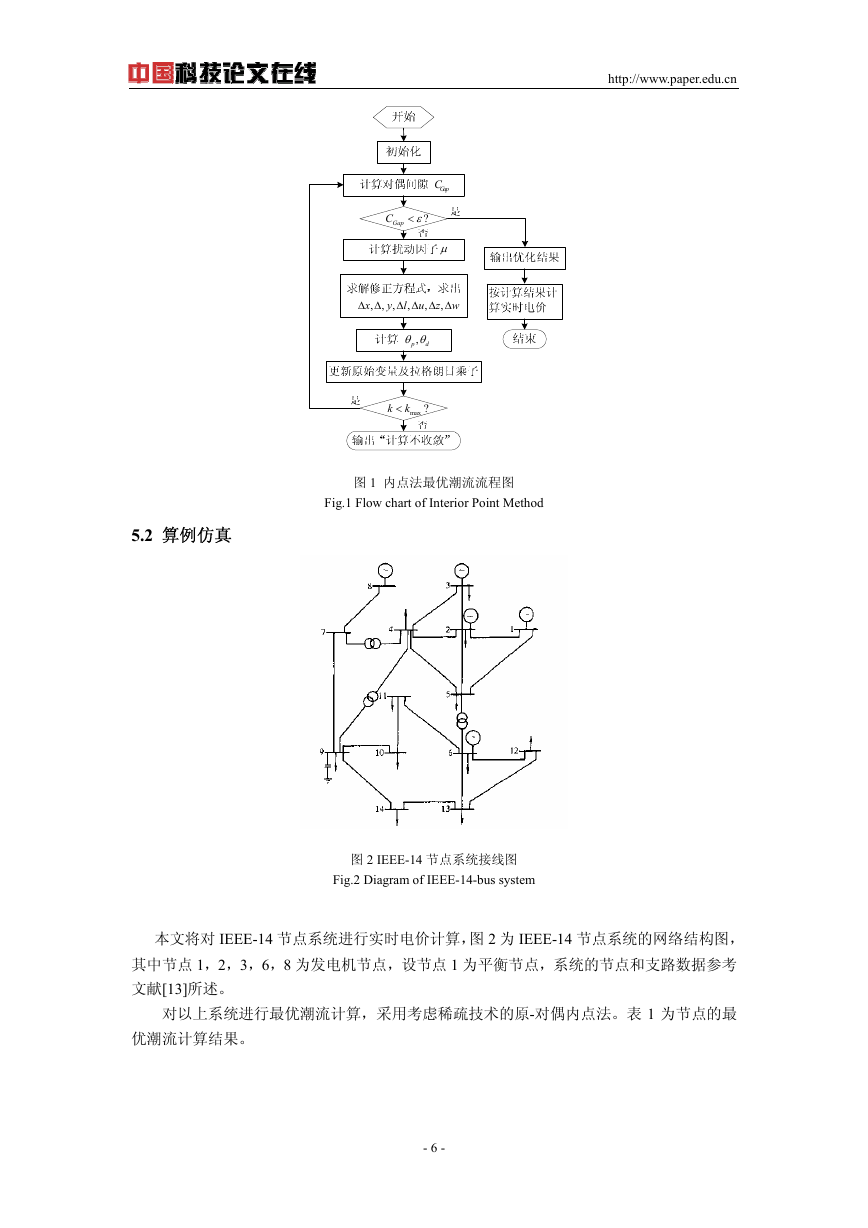
http://www.paper.edu.cn GapC ? ε< GapC µ x ∆ ∆ , , y , l ∆ ∆ ∆ ∆ z w , , u , ,p dθ θ k k< max ? 图 1 内点法最优潮流流程图 Fig.1 Flow chart of Interior Point Method 5.2 算例仿真图 2 IEEE-14 节点系统接线图 Fig.2 Diagram of IEEE-14-bus system 本文将对 IEEE-14 节点系统进行实时电价计算，图 2 为 IEEE-14 节点系统的网络结构图，其中节点 1，2，3，6，8 为发电机节点，设节点 1 为平衡节点，系统的节点和支路数据参考文献[13]所述。对以上系统进行最优潮流计算，采用考虑稀疏技术的原-对偶内点法。表 1 为节点的最优潮流计算结果。 - 6 -

http://www.paper.edu.cn 表 1 节点最优潮流计算结果 Tab. 1 Optimal power flow result of nodes for IEEE-14 bus sample system 节点 1 2 3 4 5 6 7 8 9 10 11 12 13 14 电压发电机功率负荷功率 V (p.u.) θ (°) Ps(MW) Qs(Mvar) Pd(MW) Qd(Mvar) 1.062 1.050 1.013 1.021 1.028 1.029 1.023 1.025 1.024 1.021 1.023 1.020 1.018 1.010 总的功率 0.00 -1.970 -9.431 -7.451 -6.220 -11.087 -10.177 -9.685 -11.960 -12.216 -11.847 -12.149 -12.239 --13.381 119.92 132.42 5.00 －－ 5.0 － 5.0 －－－－－－ 267.33 2.1 0.95 1.59 －－ 1.59 － 1.17 －－－－－－ 7.40 － 21.70 94.20 47.80 7.60 11.20 －－ 29.50 9.00 3.50 6.10 13.50 14.90 259.00 － 0.00 0.00 0.00 0.00 0.00 －－ 16.60 0.00 0.00 0.00 0.00 0.00 16.60 最小燃料费用 3745.01 ($ / h) 节点实时电价 ($/MWh、$/Mvar) 有功无功电价电价 0.028 12.398 12.648 0.014 0.326 11.624 0.078 13.382 0.077 13.025 13.211 0.103 0.085 13.395 0.085 13.394 13.404 0.088 0.091 13.451 0.098 13.379 0.108 13.440 13.514 0.109 0.104 13.745 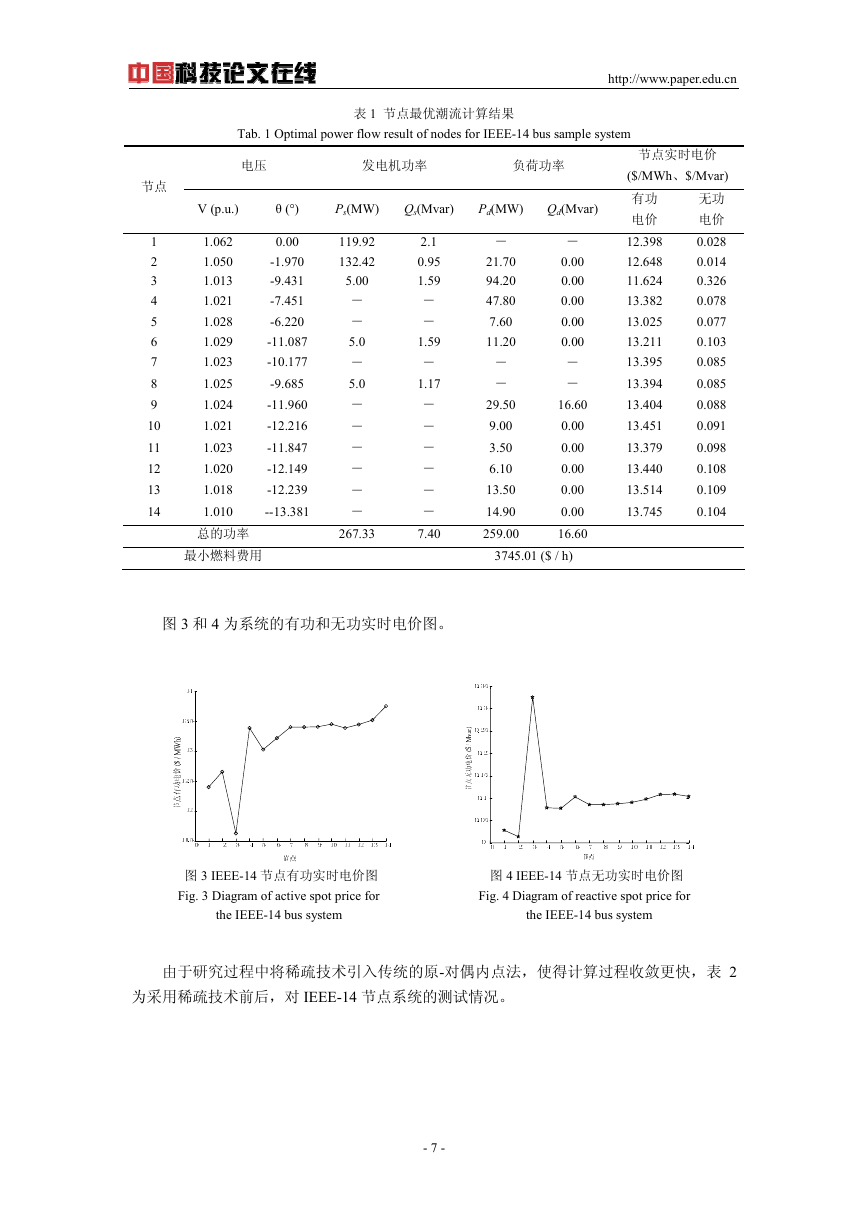图 3 和 4 为系统的有功和无功实时电价图。图 3 IEEE-14 节点有功实时电价图图 4 IEEE-14 节点无功实时电价图 Fig. 3 Diagram of active spot price for Fig. 4 Diagram of reactive spot price for the IEEE-14 bus system the IEEE-14 bus system 由于研究过程中将稀疏技术引入传统的原-对偶内点法，使得计算过程收敛更快，表 2 为采用稀疏技术前后，对 IEEE-14 节点系统的测试情况。 - 7 -

http://www.paper.edu.cn 表 2 采用稀疏技术前后的计算结果比较 Tab. 2 Comparison of computation results for the use of sparse technology 系统 IEEE-14 节点系统方法传统原-对偶内点法考虑稀疏后的原-对偶内点法迭代次数计算时间优化后发电费用 12 次 13 次 30 ms 12 ms 3 745.01 $ / h 3 745.01 $ / h 通过表中数据可以看出，采用稀疏技术能够大大加快原-对偶内点法的收敛速度，但不影响收敛的结果，能够较好地满足电力市场实时电价的计算要求。 6. 结果分析优化前，系统的有功损耗为 13.275MW，无功损耗为 54.76MVAR；而优化后，系统的有功损耗为 8.334MW，无功损耗为 35.54MVAR，显然，优化后的损耗要少的多。同时，优化后的燃料费用为 3 745.01$/h；而优化前的燃料费用为 3848.2$/h。通过对计算结果的分析还可以看出，传输线路的约束影响节点电价。当某线路的线路约束越界时（改变该线路的线路约束），节点电价（除流出节点）都在增加。如，当线路 1-2 的功率极限降低到 65MW 时，在计算过程中可以发现节点 2 的电价增加，而节点 1 的电价降低，造成其他节点的电价也相应增加。这是由于线路约束使得采用损耗大的线路来通过，同时重新分配发电机的出力，使得总的运行成本增加。参考文献 [1] [2] [3] [4] Einborn M, Siddiqi R. Electricity Transmission Pricing and Technology[J]. Kluwer Academic Publishers, 1996. River M, Perea-Ariaga I. Computation and Decomposition of Spot Price for Transmission Pricing[C]. In: 11 PSCC Conference, 1991. Ray D, Alvarado F. Use of an Engineering Model for Economic Analysis in the Electric Utility Industry[C]. In: Advanced Workshop on Regulation and Public Utility Economics. Rutgers University, 1988. Baughman M L, Siddiq S N. Real Time Pricing of Reactive Power: Theory and Case Study Results. IEEE Trans. on Power Systems, 1991,6(1). [5] Dandachi N, Rawlins M, Alsac O, et al. OPF for Reactive Pricing Studies on the NGC System. IEEE Trans. on Power Systems, 1996,11(1). [6] 于尔铿, 韩放, 谢开等. 电力市场 [M]. 北京: 中国电力出版社, 1998. [7] 华栋, 王玮, 张平. 输电服务的定价模式及方法 [J]. 武汉水利电力大学学报(社会科学版), 2000(5). [8] 姚建刚, 章建. 电力市场 [M]. 北京: 高等教育出版社, 1999. [9] 侯芳. 实时电价与输电定价的算法研究[D]. 湖南大学硕士论文, 2002. [10] Yue Yuan, J. Kubokawa, H. Sasaki. A Solution of Optimal Power Flow with Multi-Contingency Transient Stability Constraints [J]. IEEE Transactions on Power Systems, 8(3), 2003. [11] Yue Yuan, J. Kubokawa, H. Sasaki. A Study of Transient Stability Constrained Optimal Power Flow with Multi-Contingency [J]. Transactions of Institute of Electrical Engineers of Japan, 122-B(7), 2002. [12] David I. Sun, Bruce Ashley, et al. Optimal Power Flow By Newton Approach [J]. IEEE Trans. on Power Apparatus and Systems, Vo1.PAS-103, No.l0, October 1984. [13] 吴际舜, 侯志检. 电力系统潮流计算的计算机方法[M]. 上海：上海交通大学出版社，2000. - 8 -

资料库

基于原-对偶内点法的电力市场实时电价计算.pdf

相关推荐

开发技术

热门标签

最新资料