粒子群优化算法的研究现状.pdf-资料库

wjw1018-2388084-4744302542913523234.pdf-第1页.png

第1页 / 共7页

wjw1018-2388084-4744302542913523234.pdf-第2页.png

第2页 / 共7页

wjw1018-2388084-4744302542913523234.pdf-第3页.png

第3页 / 共7页

wjw1018-2388084-4744302542913523234.pdf-第4页.png

第4页 / 共7页

wjw1018-2388084-4744302542913523234.pdf-第5页.png

第5页 / 共7页

wjw1018-2388084-4744302542913523234.pdf-第6页.png

第6页 / 共7页

wjw1018-2388084-4744302542913523234.pdf-第7页.png

第7页 / 共7页

西安建大科技/总第 62 期/2005 第 2 期 ● 科研论文粒子群优化算法及其应用于帆 *，范娜（西安建筑科技大学，陕西西安 710055）【摘要】粒子群优化(PSO)算法是一种新颖的演化算法，它属于一类随机全局优化技术，PSO 算法通过粒子间的相互作用在复杂搜索空间中发现最优区域。PSO 的优势在于简单而又功能强大。本文介绍了基本的 PSO 算法、研究现状及其应用，并讨论将来可能的研究内容。关键词：粒子群优化算法；演化算法；群体智能 1. 1 引言从 20 世纪 90 年代初，就产生了模拟自然生物群体 (swarm) 行为的优化技术。 Dorigo等人从生物进化的机理中受到启发，的，但是整个生物群体却表现出处理复杂问题的能力，群体智能就是这些团体行为在人工智能问题中的应用。粒子群优化(PSO)最初是处理连续优化问题的，目前其应用已扩通过模拟蚂蚁的寻径行为，提出了蚁群优化展到组合优化问题[2]。方法；美国学者R.C.Eberhart和J.Kennedy 于 1995 年提出的粒子群优化 (Particle Swarm Optimization)算法是基于对鸟群、鱼群的模拟[1]。这些被称为群体智能(Swarm intelligence)。通常单个自然生物并不是智能同遗传算法(Genetic Algorithm，GA)、蚁群优化等大多数进化计算方法一样，PSO 也是一种基于群体的优化方法。但与其它进化计算方法相比，PSO 的主要特点为：l)每一个体(称为一个粒子)都被赋予了一个随机 * 作者简介：于帆，（1976— ）女，内蒙古赤峰市人，硕士系统工程专业，研究方向，优化技术研究 20

速度并在整个问题空间中流动；2)个体具有不断地修正自己的前进方向和速度大小，从记忆功能；3)个体的进化主要是通过个体之而形成群体寻优的正反馈机制。PSO 算法就间的合作与竞争来实现的。作为一种高效并是这样依据每个粒子对环境的适应度将个行优化方法，PSO 可用于求解大量非线性、体逐步移到较优的区域，并最终搜索、寻找不可微和多峰值的复杂优化问题，再加上到问题的最优解。PSO 算法具有鲜明的生物 PSO 算法的程序实现异常简洁，需要调整的社会背景:认知行为和社会行为，即在寻求一参数少，因而发展很快，出现了多种改进致的认知过程中，个体往往记住它们的信 PSO 算法，并已应用于许多科学和工程领域, 念，同时考虑其它同伴的信念，当个体察觉得到了众多学者的重视和研究。同伴的信念较好时，将进行适应性调整。 2. 2 粒子群优化算法介绍在PSO算法中，用粒子的位置表示待优 2.1 算法原理化问题的解，每个粒子性能的优劣程度取决 PSO 算法不像遗传算法那样对个体进于待优化问题目标函数确定的适应值，每个行选择、交叉和变异操作，而是将群体中的粒子由一个速度矢量决定其飞行方向和速每个个体视为多维搜索空间中一个没有质率大小。设在一个d维的目标搜索空间中，量和体积的粒子(点)，这些粒子在搜索空间有m个粒子组成一个群体，其中，在第t次迭中以一定的速度飞行，并根据粒子本身的飞代时粒子 i 的位置表示为 Xi(t)=(xi1(t) ，行经验以及同伴的飞行经验对自己的飞行 xi2(t)，…，xid(t))，相应的飞行速度表示为速度进行动态调整，即每个粒子通过统计迭 Vi(t)=(vi1(t)，vi2(t)，…，vid(t))。开始执行PSO 代过程中自身的最优值和群体的最优值来算法时，首先随机初始化m个粒子的位置和 21

速度，然后通过迭代寻找最优解，在每一次细搜索以获得高精度的解;c 1、c2:为两个学习迭代中，粒子通过跟踪两个极值来更新自己因子，一般取为 2;randl和rand2 为两个均匀的速度和位置:一个极值是粒子本身迄今搜分布在(0，l)之间的随机数;i=1，2，…，m; 索到的最优解，称为个体极值，表示为 k=1，2，…，d。另外，粒子在每一维的速 Pi(t)=(pi1(t)，pi2(t)，…，pid(t));另一个极值是度Vi都被一个最大速度Vmax所限制。如果当整个粒子群到目前为止找到的最优解，称为前粒子的加速度导致它在某一维的速度超全局极值，表示为Pg(t)=(pg1(t)，pg2(t)，…，过该维上的最大速度Vmax，则该维的速度被 pgd(t))。在第t+1 次迭代计算时，粒子i根据限制为最大速度。式①中第 1 部分可理解为下列规则来更新自己的速度和位置：粒子先前的速度或惯性；第 2 部份可理解为 Vik(t+l)= ω ν ik (t)+c1 randl (pik(t) －粒子的“认知”行为，表示粒子本身的思考能 xik(t))+c2 rand2 ① (pgk(t) － xik(t)) 力;第 3 部分可理解为粒子的“社会”行为，表示粒子之间的信息共享与相互合作。 Xik(t+l)=xik(t)+ νik (t+l) ② 2.2 算法流程式中ω为惯性权重，ω取大值可使算法标准PSO算法流程[2]如下: 具有较强的全局搜索能力，ω取小值则算法倾向于局部搜索。一般的做法是将ω初始取 0.9 并使其随迭代次数的增加而线性递减至 0.4，这样就可以先侧重于全局搜索，使搜索空间快速收敛于某一区域，然后采用局部精 22 (1)随机初始化粒子群体的位置和速度; 通常是在允许的范围内随机产生的,每个粒子的 pbest 坐标设置为其当前位置,且计算出其相应的个体极值(即个体的适应度值), 而全局极值(即全局的适应度值)就是个体极

值中最好的,记录该最好值的粒子序号,并将达到则停止计算。PSO 算法可用伪代码表示 gbest 设置为该最好粒子的当前位置; 如下： (2)计算每个粒子的适应值; 初始化粒子群; (3)对每个粒子，将其适应值与个体极值 DO 进行比较，如果较优，则更新当前的个体极值; (4)对每个粒子，将其适应值与全局极值 For 每个粒子计算其适应度; If (适应度优于粒子历史最佳值) 用Xi更新历史最佳个体Pi; End 选取当前粒子群中最佳粒子; 进行比较，如果较优，则更新当前的全局极 If (当前最佳粒子优于群历史最佳粒子) 值; (5)根据式①、②，更新每个粒子的位置和飞行速度; (6)如未达到预先设定的停止准则(通常设置为最大迭代次数)，则返回步骤(2)，若用当前群最佳粒子更新Pg; For 每个粒子按式①更新粒子速度; 按式②更新粒子位置; End While 最大迭代数未达到或最小误差未达到。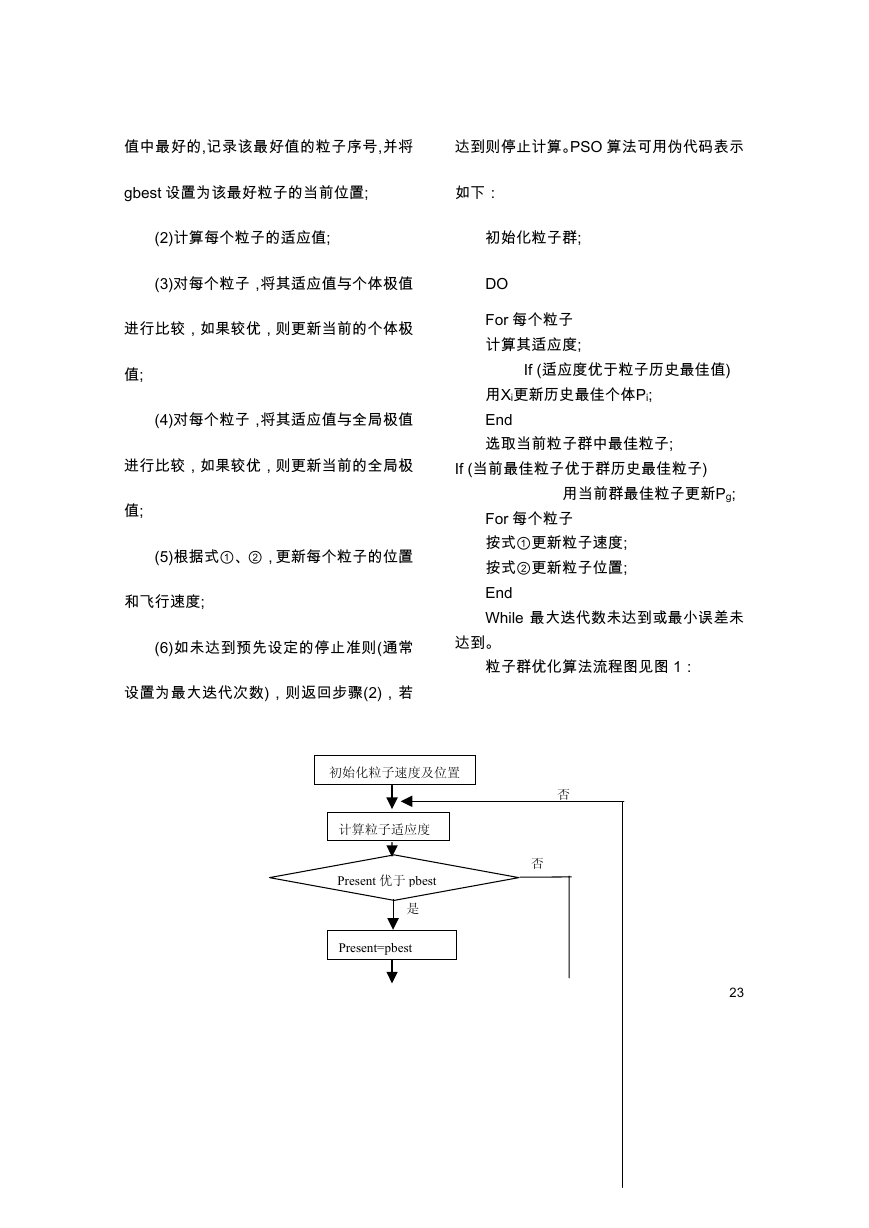粒子群优化算法流程图见图 1：初始化粒子速度及位置计算粒子适应度否否是 Present 优于 pbest Present=pbest 23

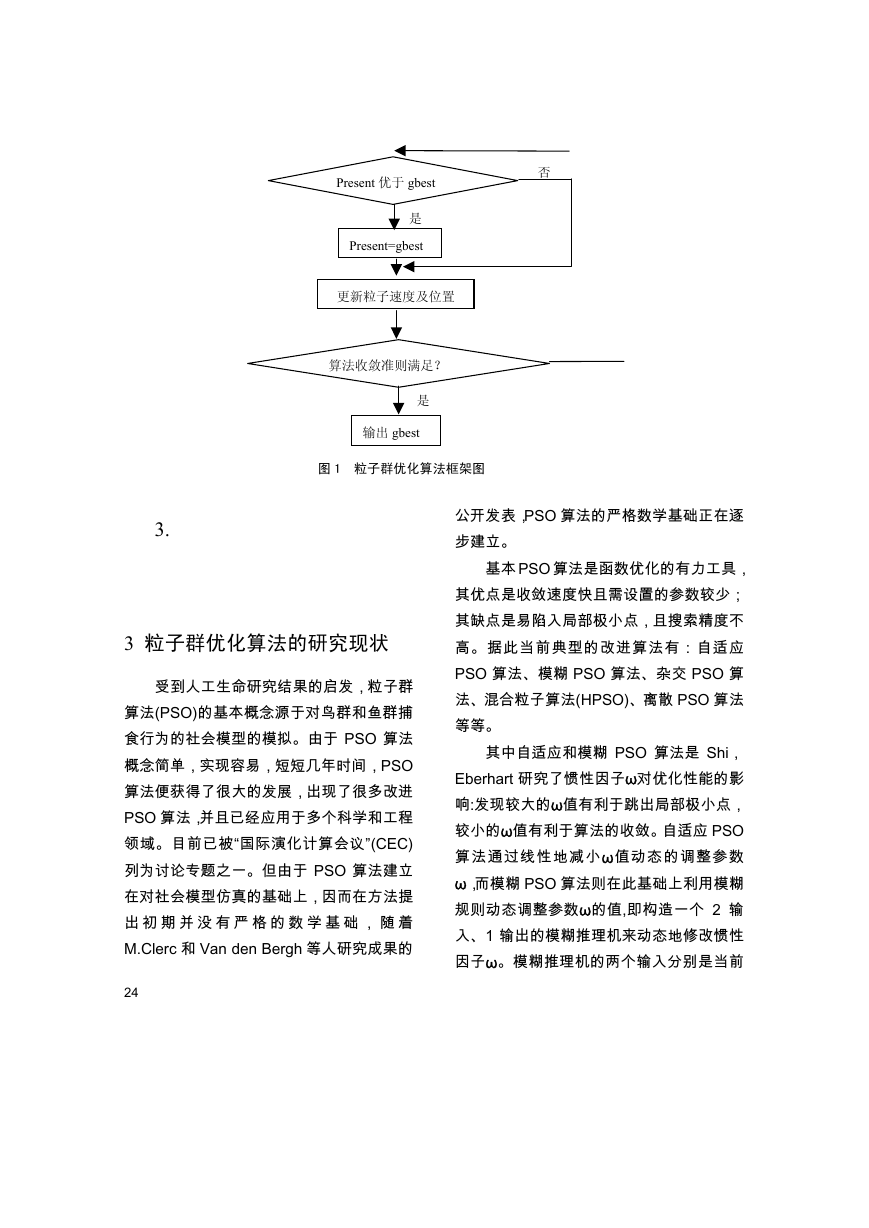
Present 优于 gbest 否是 Present=gbest 是更新粒子速度及位置算法收敛准则满足？输出 gbest 图 1 粒子群优化算法框架图 3. 3 粒子群优化算法的研究现状受到人工生命研究结果的启发，粒子群算法(PSO)的基本概念源于对鸟群和鱼群捕食行为的社会模型的模拟。由于 PSO 算法概念简单，实现容易，短短几年时间，PSO 算法便获得了很大的发展，出现了很多改进 PSO 算法，并且已经应用于多个科学和工程领域。目前已被“国际演化计算会议”(CEC) 列为讨论专题之一。但由于 PSO 算法建立在对社会模型仿真的基础上，因而在方法提出初期并没有严格的数学基础，随着 M.Clerc 和 Van den Bergh 等人研究成果的 24 公开发表，PSO 算法的严格数学基础正在逐步建立。基本 PSO 算法是函数优化的有力工具，其优点是收敛速度快且需设置的参数较少；其缺点是易陷入局部极小点，且搜索精度不高。据此当前典型的改进算法有：自适应 PSO 算法、模糊 PSO 算法、杂交 PSO 算法、混合粒子算法(HPSO)、离散 PSO 算法等等。其中自适应和模糊 PSO 算法是 Shi， Eberhart 研究了惯性因子ω对优化性能的影响:发现较大的ω值有利于跳出局部极小点，较小的ω值有利于算法的收敛。自适应 PSO 算法通过线性地减小ω值动态的调整参数 ω，而模糊 PSO 算法则在此基础上利用模糊规则动态调整参数ω的值,即构造一个 2 输入、1 输出的模糊推理机来动态地修改惯性因子ω。模糊推理机的两个输入分别是当前

ω值，以及其适应度;而输出是ω的增量。杂交和混合粒子算法(HPSO)是受遗传算法、自然选择机制的启示，将遗传算子与基本 PSO 相结合而得。其中，混合 PSO 算法是将基本 PSO 算法和选择机制相结合而成，基本 PSO 算法的搜索过程很大程度上依赖 pbest 和 gbest，它的搜索区域受到 pbest 和 gbest 的限制。在通常的遗传算法中，选择机制用来选择相对较好的区域和淘汰较差的区域，可以更合理地分配有限的资源。杂交 PSO 在基本 PSO 中引入了杂交算子，两者均取得了满意的结果，改善了算法的性能。离散二进制版PSO算法是用来解决工程实际中的组合优化问题。R.A.Eberhart等在提出的模型中将每一维xid和pbestid限制为 1 或者为 0，而速度vid不作这种限制。用速度来更新位置时，如果vid高一些，粒子的位置xid更有可能选 1，vid低一点则选 0，阈值在[0，l]之间。而有这种特点的函数就是 Sig moid函数: k idv k+1 k+1 k idv k+1 k+1 k+1 then = 1; )) )=l/(l+exp(- sig( 二进制版本 PSO 的公式为 idρ < sig idv idx if idx = 0 else idρ 的各个分量是[0，1]之间的随向量机数。为了防止 Sig moid 函数饱和，可以将 idv 钳位在[-4.0，+4.0]之间。二进制 PSO 其它部分与基本连续 PSO 类似。实验结果显示，在大多数测试函数中，二进制 PSO 都比遗传算法速度快，尤其在问题的维数增加时。 k 基本 PSO 算法是求解连续函数优化的有力工具，但对离散问题却无能为力。因此 J.Kenndy 和 R.A.Eberhart 又提出了离散型 PSO 算法，用于解决组合优化问题等，它在一定程度上完善发展了基本 PSO 算法，并将其应用于旅行商问题(TSP)的求解，取得了较好的结果。离散 PSO 算法扩展了基本 PSO 算法的应用领域，让人看到了 PSO 在组合优化问题中的应用前景。 4. 4 粒子群优化的应用 PSO 的优势在于算法的简洁性，易于实现，没有很多参数需要调整，且不需要梯度信息。PSO 是非线性连续优化问题、组合优化问题和混合整数非线性优化问题的有效优化工具[2]。目前已经广泛应用于函数优化、神经网络训练、模糊系统控制以及其他遗传算法的应用领域。PSO 最初应用到神经网络训练上在随后的应用中，PSO 又可以用来确定神经网络的结构。文献[5]中用改进的速度更新方程训练模糊神经网络。Parsopoulos 等将 PSO 用于解决多目标优化问题和最小最大化问题、整数规划问题和定位所有全局极值等问题。一般说来，PSO 比较有潜力的应用包括系统设计、多目标优化、分类、模式识别、调度、信号处理、决策、机器人应用等。其中具体应用实例有:模糊控制器设计、车间作业调度、机器人实时路径规划、自动目标检测、时频分析等[3] 。总之，PSO 算法的应用十分广泛，它有着比较好的发展前景，值得做进一步的研究。 5. 5 未来的研究 25

PSO 算法是一个新的基于群体智能的进化算法，其研究刚刚开始，远没有像遗传算法和模拟退火算法那样形成系统的分析方法和一定的数学基础，有许多问题还需要进一步研究： 1)适用范围。PSO 算法应用得最成功的是在进化神经网络方面，其它的一些应用许多还停留在研究阶段。显然，PSO 算法不会仅仅局限于目前的这些领域，如果将 PSO 算法引入机器学习、自动控制等领域，将大大地促进算法的研究与发展。 2)参数的选择与设计。 PSO 算法中参数的选择依赖于具体问题，设计合适的参数需要经过多次试验。研究如何选择和设计参数，使其减少对具体问题的依赖，也将大大促进 PSO 算法的发展和应用。 6. 6 结束语粒子群优化算法是一种新兴的有潜力的演化算法，在实际应用中被证明是有效的同时，还存在一些问题，如在给出其收敛性、收敛速度估计等方面的数学证明还没有，其理论和数学基础的研究还不够。 PSO在理论上并不能保证能够得到最优解。PSO算法在进行优化问题的求解时应用范围有限，尤其对离散的组合优化问题，其理论建模还处于起步阶段。PSO算法中的一些参数如学习因子c1，c2,惯性权重ω，以及粒子个数往往根据有限的应用经验确定，并不具有广泛的适应性。因此将PSO与进化算法、模糊系统、神经网络以及一些优化技术结合，根据不同的优化问题建立相应的PSO模型是PSO算法当前的研究重点。目前我国已有学者开始了对PSO算法的研究[4]，希望PSO可以为优化研究工作带来更多的新思路。（转第 27 页） 26

资料库

粒子群优化算法的研究现状.pdf

相关推荐

开发技术

热门标签

最新资料