2 2 2 第 28 卷 第 9 期 　 　　　 　　华 　中 　理 　工 　大 　学 　学 　报 　　　　 　　　Vol. 28 　No. 9 2000 年 　9 月 　　　　 　　　J . Huazhong Univ. of Sci. & Tech. 　　　　　　　　Sep. 　 2000 基于小波变换的三维温度场重建 彭劲松 　黄素逸 (华中理工大学动力工程系) 摘要 : 建立了基于小波变换的三维温度场重建的新算法. 与传统的变换法和级数展开法相比 ,该算法不仅能 分析信号的空间 频率特性 ,滤除噪声 ,而且能实现有限角重建 ,是一种实用性较好的算法. 通过数值模拟计 算 ,对小波变换法的重建效率和精度与 SAR T 及 AR T 作了对比. 关 　键 　词 : 温度场 ;小波变换 ;重建 中图分类号 : T K311 　　文献标识码 : A 　　文章编号 : 1000 8616 (2000) 09 0076 03 　　基于小波变换的三维温度场重建法是一种新 的用于激光全息层析干涉法测量温度场的重建方 法 ,该方法既可以实现对测量信号的空 频 (空间 频率) 域分析 , 滤除噪声 , 又可以实现非完全数 据重建 (有限角重建) ,因此在三维温度场重建中 具有广泛的应用前景. M = m a m h m v m d , m a为 I 的一维低频小波分解系 数 , m h为 I 的一维水平高频小波分解系数 , m v为 I 的一维垂直高频小波分解系数 , m d为 I 的一维 对角高频小波分解系数. 至此 , 对式 (2) 的求解 转换成对 1 　基于小波变换的温度场重建 采用激光全息层析干涉法测量温度场时 , 测 得的是被测场折射率 f 沿测量光线的线积分值 s ,重建过程即为由 s 求解 f 的过程[1 ]. 采用小波 变换重建时 ,首先将待建场划分为 K 个网格. 设 f k 为第 k 个网格内的折射率值 , sm为第 m 条光线 折射率线积分值 , I m , k为第 m 条光线与第 k 个网 格截距 , I m , k可以通过几何方法或解析代数方法 求得. 然后建立线性方程组 aS dS = m a m h m v m d a F d F 的求解. 解出 U 后 ,通过小波重构即可计算出 F , 即折射率场的分布 f k . 再通过换算可得到温度场 分布 , 完成重建. 事实上 , 使用上述方法进行温度 场重建时 ,可以对 V , U 和 M 进行多重分解 ,如 : U = [ a F , d F - 1 , d F - 2 , …, d Fj , …] T ,重构时 , 通过将 d Fj 置 0 ,即可实现任意频段滤波. 对于二 维分解 ,由 a F 和 d F 重构 F 时 , 若以 0 替代 d F , 则可实现低频重建. S = I ·F , 式中 , S = [ S 1 , S 2 , …, S M ] T ; F = [ f 1 , (1) f 2 , …, 2 　数值模拟计算 f K ] T ; I = I11 I12 … I1 K I22 … I2 K I21 … … … … IM 2 … IM K IM 1 . 由文献 [2 ] ,对 于求解式 (1) 的问题可变换为解 V = M ·U , (2) 式中 , V 和 U 为分块向量 , 其元素分别是向量 S 和 F 的 小 波 分 解 系 数 , 以 二 维 分 解 为 例 , V = [ aS 　dS ] T , U = [ a F 　d F ] T. M 为一分块距阵 , 对任一双高斯分布函数及叠加了高频噪声的 同一双高斯分布函数 ,分别采用小波分解法 、联合 代数法 ( SAR T) 及代数法 (AR T) 重建. 据文献 [3 ] ,定义误差 e = ∑ ∑ 式中 , ^f ij为点 ( i , j) 处重建值 ; f ij为同一点的实 际值 ;珔f ij为实际分布的平均值. 2. 1 　模拟计算结果 f ij | 2 ∑ f ij - 珔f ij | 2 , ∑ | | ^f ij - i = 1 j = 1 i = 1 j = 1 N M N M 图 1 ～ 图 4 为 采 用 小 波 全 频 、小 波 低 频 、 01 收稿日期 : 2000 11. 作者简介 : 彭劲松 (1967 基金项目 :国家教育部重点科学技术项目. ) ,男 ,博士研究生 ;武汉 ,华中理工大学动力工程系 (430074) . © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net 

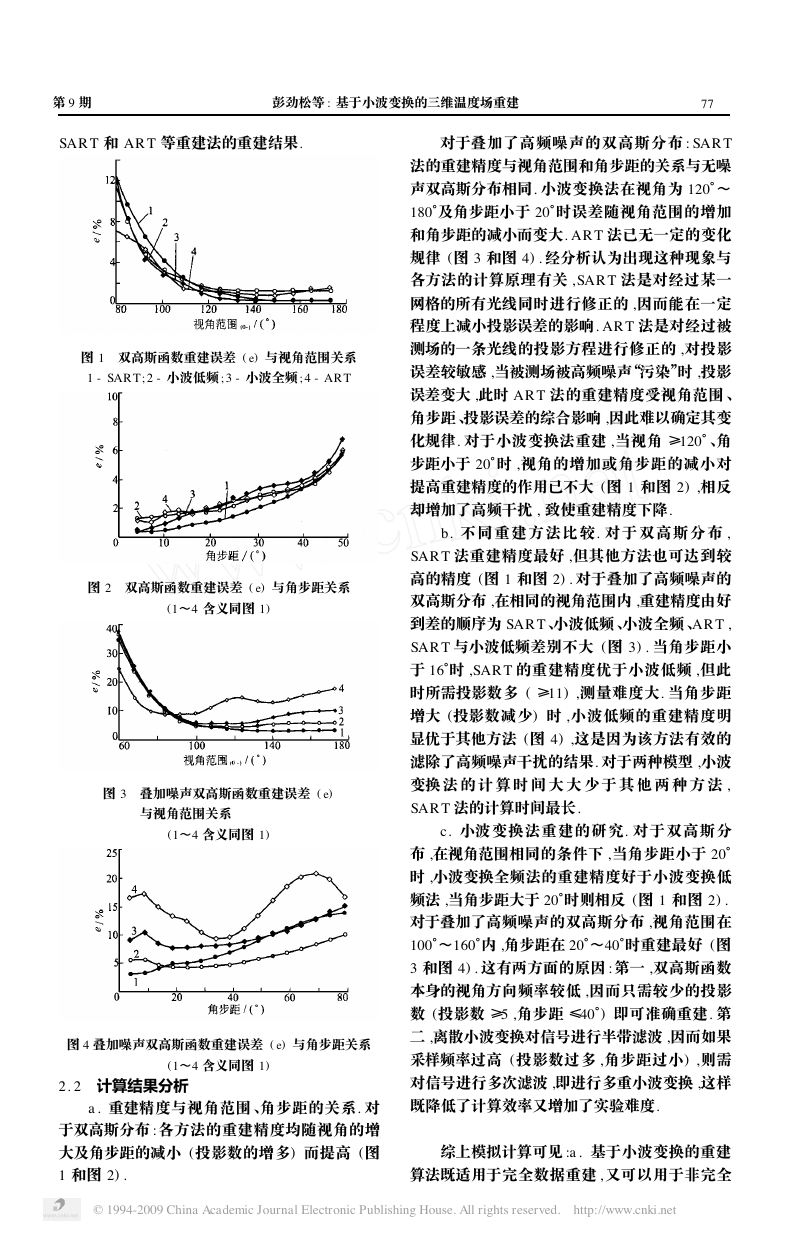
第 9 期 　　　　　 　　　　　 　　　彭劲松等 : 基于小波变换的三维温度场重建 　　　　　　　　　 　　　　　　　 77 SAR T 和 AR T 等重建法的重建结果. 图 1 　双高斯函数重建误差 ( e) 与视角范围关系 1 - SAR T;2 - 小波低频 ;3 - 小波全频 ;4 - AR T 图 2 　双高斯函数重建误差 ( e) 与角步距关系 (1～4 含义同图 1) 图 3 　叠加噪声双高斯函数重建误差 ( e) 与视角范围关系 (1～4 含义同图 1) 图 4 叠加噪声双高斯函数重建误差 ( e) 与角步距关系 (1～4 含义同图 1) 2. 2 　计算结果分析 a. 重建精度与视角范围 、角步距的关系. 对 于双高斯分布 :各方法的重建精度均随视角的增 大及角步距的减小 (投影数的增多) 而提高 (图 1 和图 2) . 对于叠加了高频噪声的双高斯分布 : SAR T 法的重建精度与视角范围和角步距的关系与无噪 声双高斯分布相同. 小波变换法在视角为 120°～ 180°及角步距小于 20°时误差随视角范围的增加 和角步距的减小而变大. AR T 法已无一定的变化 规律 (图 3 和图 4) . 经分析认为出现这种现象与 各方法的计算原理有关 , SAR T 法是对经过某一 网格的所有光线同时进行修正的 ,因而能在一定 程度上减小投影误差的影响. AR T 法是对经过被 测场的一条光线的投影方程进行修正的 ,对投影 误差较敏感 ,当被测场被高频噪声“污染”时 ,投影 误差变大 ,此时 AR T 法的重建精度受视角范围 、 角步距 、投影误差的综合影响 ,因此难以确定其变 化规律. 对于小波变换法重建 ,当视角 ≥120°、角 步距小于 20°时 ,视角的增加或角步距的减小对 提高重建精度的作用已不大 (图 1 和图 2) ,相反 却增加了高频干扰 , 致使重建精度下降. b. 不 同 重 建 方 法 比 较. 对 于 双 高 斯 分 布 , SAR T 法重建精度最好 ,但其他方法也可达到较 高的精度 (图 1 和图 2) . 对于叠加了高频噪声的 双高斯分布 ,在相同的视角范围内 ,重建精度由好 到差的顺序为 SAR T、小波低频 、小波全频 、AR T , SAR T 与小波低频差别不大 (图 3) . 当角步距小 于 16°时 ,SAR T 的重建精度优于小波低频 ,但此 时所需投影数多 ( ≥11) ,测量难度大. 当角步距 增大 (投影数减少) 时 ,小波低频的重建精度明 显优于其他方法 (图 4) ,这是因为该方法有效的 滤除了高频噪声干扰的结果. 对于两种模型 ,小波 变换 法 的 计 算 时 间 大 大 少 于 其 他 两 种 方 法 , SAR T 法的计算时间最长. c. 小波变换法重建的研究. 对于双高斯分 布 ,在视角范围相同的条件下 ,当角步距小于 20° 时 ,小波变换全频法的重建精度好于小波变换低 频法 ,当角步距大于 20°时则相反 (图 1 和图 2) . 对于叠加了高频噪声的双高斯分布 ,视角范围在 100°～160°内 ,角步距在 20°～40°时重建最好 (图 3 和图 4) . 这有两方面的原因 :第一 ,双高斯函数 本身的视角方向频率较低 ,因而只需较少的投影 数 (投影数 ≥5 ,角步距 ≤40°) 即可准确重建. 第 二 ,离散小波变换对信号进行半带滤波 ,因而如果 采样频率过高 (投影数过多 ,角步距过小) ,则需 对信号进行多次滤波 ,即进行多重小波变换 ,这样 既降低了计算效率又增加了实验难度. 综上模拟计算可见 :a. 基于小波变换的重建 算法既适用于完全数据重建 , 又可以用于非完全 © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net 

87　　　 　　　　　　　　　　　　　　华 　中 　理 　工 　大 　学 　学 　报 　　　　　　　　　　　　　　2000 年 数据重建 ;既能实现全频重建 ,又可实现低频重建 以滤掉高频噪声的干扰 ,且所需投影数较少 ,是一 种实用性较好的算法. b. 与 SAR T 和 AR T 相比 , 小波变换法的计算速度是最快的. c. 对于双高斯 型分布的温度场 ,采用小波变换法 (低频) 重建 时 ,在视角范围大于 100°,角步距为 20°～40°时 , 可得到较好的重建效果. 1990. [ 2 ] Wang Gaofeng , Zhang J un , Pan Guangwen. Solution of Inverse Problems in Image Processing by Wavelet Ex pansion. IEEE Transaction on Image Processing , 1995 , 4 (5) : 579～593 [3 ] Andersen A H. Algebraic Reconstruction in CT from IEEE Ttansactions on Medical Imag Limited Views. ing , 1989 , 8 (1) : 50～55 参 考 文 献 [ 1 ] 朱德忠. 热物理激光测试技术. 北京 : 科学出版社 , Reconstruction of Wavelet Based 3 D Temperature Field Peng Ji nsong 　Huang S uyi Abstract : Based on Wavelets base t heory , a new approach to 3 D temperature field reconstruction is estab lished. Compared wit h t he traditional reconstruction approaches , Transform met hods and Series expansion met hods , t he signal spatial frequency feature are not only analyzed , getting rid of t he noise effectively , but also limited view reconstruction can be done. The reconstruction efficiency and accuracy of t his met hod is contrasted wit h SAR T and AR T t hrough an analogous computation. Key words : temperature field ; Wavelet transform ; reconstruction Pen Jingsong 　Doctoral Candidate ; Dept . of Power Eng. , HUST , Wuhan 430074 , China. 华中理工大学专业介绍 (十一) 材料科学与工程学院 (四年制) 　　本院设有博士后流动站 、三个博士点 、一个硕士点 ,本科专业有材料 科学与工程 、材料成型与控制工程两个宽口径专业. 现有中国工程院院士 1 名 、博士生导师 21 名. 材料科学与工程专业 　主要学习材料科学与工程的基础理论 ,本专 业的学生受到各种先进材料的制备 、性能分析与检测技能的基本训练 ,掌 握材料设计和制备设计 ,提高材料性能和产品的质量 、开发研究新材料和 新工艺方面的基本能力. 主要课程有 :材料科学基础 、材料物理 、材料化 学 、材料力学 、材料显微分析 、纳米及非晶态材料 、表面工程学 、计算机在 材料科学中的应用. 材料成型与控制工程专业 　主要学习材料科学及各类热加工工艺的 基础理论与技术和有关设备的设计方法 ,本专业的学生受到现代机械工 程师的基本训练 ,具有从事各类热加工工艺及设备设计 、生产组织管理的 基本能力. 主要课程有 :材料科学基础 、材料成型工艺基础及设备 、材料成 型计算机控制 、检测技术 、现代模具设计 、CAD/ CAM 基础 、材料成型计算 机模拟. 毕业生就业面广 ,可以到企业 、科研设计院所从事应用开发 、生产组 织管理 、设计研究等工作 ,还可到高等院校从事科研和教学工作. © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net