logo资料库

能带图分析.pdf

发布时间：2022-06-08 发布人：admin 分类：说明书 资料大小：0.37M 资料格式：pdf 举报 版权申诉
第1页 / 共10页
第2页 / 共10页
第3页 / 共10页
第4页 / 共10页
第5页 / 共10页
第6页 / 共10页
第7页 / 共10页
第8页 / 共10页
资料共10页，剩余部分请下载后查看
    能带结构和态密度图的绘制及初步分析 前几天在 QQ 的群中和大家聊天的时候，发现大家对能带结构和态密度比较感兴趣，我 做计算已经有一年半了，有一些经验，这里写出来供大家参考参考，希望能够对初学者有所 帮助，另外写的这些内容也不可能全都正确，只希望通过表达出来和大家进行交流，共同提 高。 MS 这个软件的功能确实是比较强，但是也有一些地方不尽如人意的地方。（也可能是 我对一些结果不会分析所致，有些暂时不能解决的问题在最后一部分提出，希望大家来研究 研究，看看有没有实现的可能性）。 能带结构、态密度和布居分析是很重要的内容，在 分析能带结构和态密度的时候，往往是先作图，然后分 析。 软件本身提供的作图功能并不是很强，比如说能带结构 （只能带只能做 point 图和 line 图），不美观不说，对于 每一个能带的走势也不好观察，感觉无从下手。所以我 一般用 origin 作图（右图是用 origin 做的能带图）。能带 结构和态密度的作图过程请参考我给大家提供的动画。 接下来我们先开看看能带结构的分析和制作！ 第一部分：能带结构 这个部分打算先简单的介绍一下能带的基础知识，希望能对大家有所帮助，如果对能带 了解比较深入的朋友，可以跳过这个部分内容，之中不当之处请勿见笑。^_^ 第一个问题是： 1、能带是怎样形成——轨道和一维体系的能带。 这是最基本的一个问题，我们要对能带结构进行分析，首先要知道它是如何来的。其实 能带是一种近似的结果（可以看成一种近似），是周期边界条件（bloch 函数）下的一种近似。 先来看看一个最简单的问题，非周期体系有没有能带结构？答案是没有的，大家可以试试： ①建一个周期的晶胞 ②选择 build 菜单下的 symmetry 子菜单下的 none periodic superstructure 去掉周期边界条件性 ③看看还能够运行吗？运行（run）按钮变灰了，不能提 交作业了。这说明什么问题？这说明这个 CASTEP 这个模块不能计算非周期的体系，另外 可以参考 MS 中的 DMOL 模块，它可以计算非周期系统，虽然可以计算周期系统，但是仍 不能计算能带，大家可以试试，看看 property 中的 band structure 能不能选上，一定不能！！ ^_^ 从这里，我们可以得到一个结论，对于单个原子（分子、单胞）如果不加上周期边界条 件，是无法获得能带结构的。所以计算小分子体系，或者采用团簇模型的朋友，这部分内容 或许对你们没有帮助！那么，非周期体系的态密度能够计算吗？这应该是能够计算的，曾经 开到过文献采用团簇模型，计算出态密度的（phys. Rev. 上的文章）。 那么非周期体系为什么没有能带结构呢？ 看一个例子：一个 H2 分子有能带吗？没有，因为它没有周期边界条件，也就是说在 x， y，z 方向上没有重复，所以它没有能带结构。那 H2 分子有什么东西呢？有两个轨道，两个 1s 原子轨道，或者说两个轨道能级，它们成键参考右图。 再看另外一个例子：一维无限 H 原子链 H H H H H H 在一维无限 H 原子链体系中，产生了能带。 为什么在一维无限 H 原子链体系中能够产生能带呢？ 1
    因为，每一个 H 原子有一个 1s 轨道，由于在 X 轴方向（H 原子周期排列的方向）引入 周期边界条件，所以这个体系有无数（阿佛加得罗）个 H1s 的轨道能级，这些具有相同能 量的能级轨道处于简并的状态。如果两个相邻的 H 原子之间距离较大，不能够成键，那么 这无数个简并的能级将排成一条水平的直线，这条直线很长，无法画下来，那么我们只有压 缩它，将他压缩到一个区间（[0, π a ]），这样每一个能级用一个点表示，由于点较多，看起 来好像形成了一条线，这样能带就形成了。 如果用函数的语言来描述，周期排列我们采用 bloch 函数表示，我们解这些函数，就得 到了一些 k 矢量，在一维体系中 k 矢量表示平移操作，k 的取值见下图，由于 H1s 轨道能级 有无数个，所以 k 平移操作矢量就有无数个（注意 k 是量 子化的），所以将它们压缩到[0, π a ]这个区间，就成了能带 结构中的横坐标，另外这个矢量也可以指向-X 方向，所以在[- [0, π a ]对称。 π a ,0]这个区间能带的图像和 当 H 原子之间的距离逐渐接近，它们的原子轨道要进行组合，形成一个成键分子轨道 和一个反键分子轨道，那么原来能带是一条水平的直线，现在就要开始发生弯曲了（两个分 子轨道能量不一样，导致能带发生弯曲），所以[0, π a ]这个区间，能带开始有带宽（散度）， 随着 H 原子的距离逐渐接近，可以预料，成键分子轨道和反键分子轨道的分裂越大，能带 的带宽（最高能级－最低能级）越大。所以，相邻轨道之间的重叠越大，成键程度越大， 带宽就越大。 时，H1s 轨道组合成的分子轨道能量最高（原子轨道为＋－＋－……交替）。所以 另外值得一提的是，k 矢量还可以表示节点的数目。当 k＝0 的时候表示什么呢？表示 节点数为 0，没有节点，所以 k＝0 表示的 H1s 轨道组合（组成分子轨道的原子轨道都带＋ 号）具有最大的成键，能量最低。随着 k 值的增大，节点数逐渐增多，体系的能量上升，最 π 后 k＝ a π H 原子链的能带结构是一条向上弯曲的曲线（能带），k＝0 能量最低，k＝ a 这里要特别注意，并不是 k＝0 的时候节点数都为 0，比如（＋－，＋－，＋－，……） 这样的 p 轨道，如果它们沿着 X 轴周期排列，那么 k＝0 的时候将具有最大的节点数，这时 候形成的分子轨道将是能量最大的，随着 k 的逐渐增加，节点数逐渐减小，所以这时候能带 将向下伸展，这与 H 原子链的情况刚好相反。 时能量最高。 大家都知道，这样的 H 原子链是不可能稳定的，最后都要变成 H2 分子，能带要消失， 这是一个什么样的过程呢？在这个一维周期体系中轨道能级的数目假设为 N（无限大），那 么这个体系的电子数是多少呢？答案是 N，那么这些电子在这个能带上是如何分布的呢？当 然是按照能量从低到高的顺序来填充的了，这样由于每一个轨道能够容纳 2 个电子，而这个 能带只有较低能量的部分被填充（能带半充满），所以这时候要产生畸变（Peierls 畸变，即 固体物理中的姜－泰勒效应），H 原子之间要产生相对振动（虚模，能量不稳定），以降低体 系的能量，这样，H2 分子就形成了，而能带也由于 H2 原子的形成破坏了周期条件，当这 些 H2 分子不再沿着 X 轴方向形成周期排列的时候，能带也就消失了（变成非周期体系）。 结论：一个原子的一个原子轨道在一维周期条件下将产生一条能带，能带的带宽取决于 这些原子轨道的在周期方向上的成键强度，强度越大，带宽越大，成键越弱，带宽越小，如 2
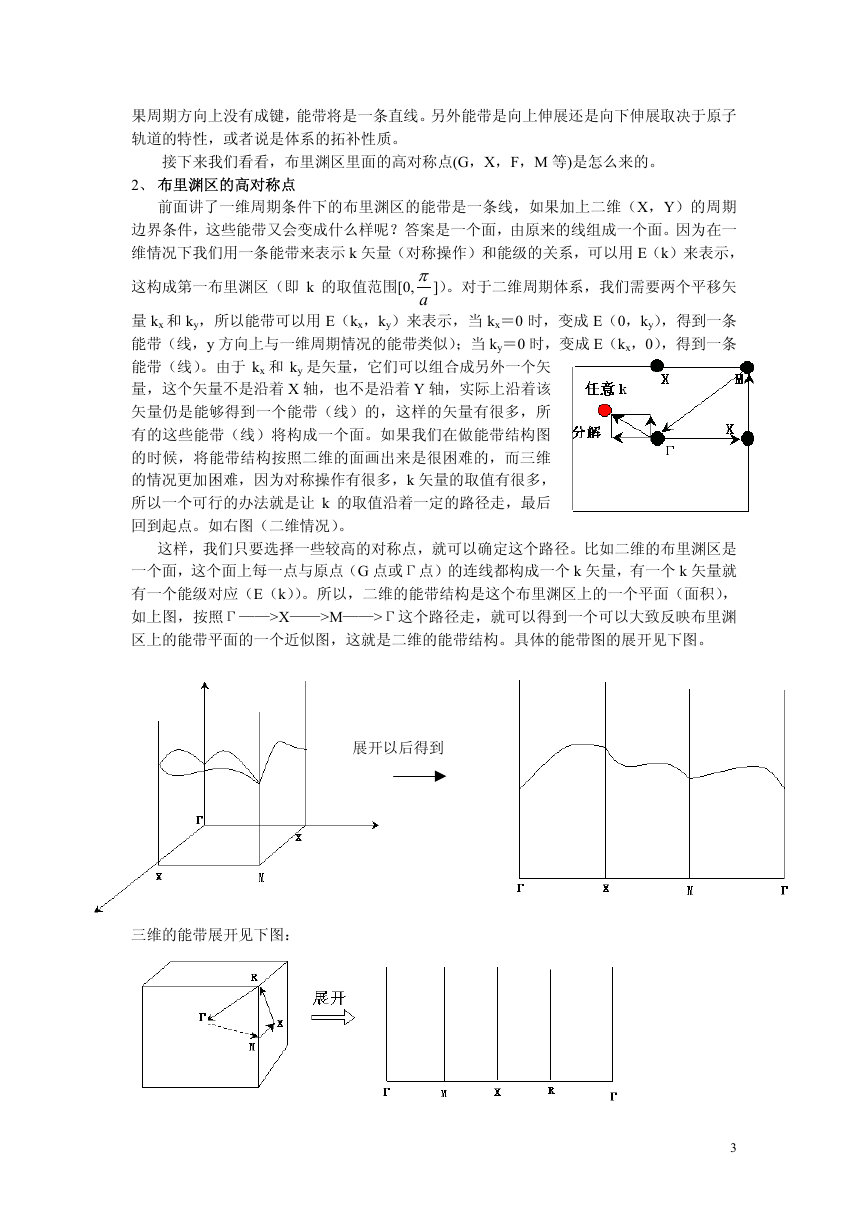
    果周期方向上没有成键，能带将是一条直线。另外能带是向上伸展还是向下伸展取决于原子 轨道的特性，或者说是体系的拓补性质。 接下来我们看看，布里渊区里面的高对称点(G，X，F，M 等)是怎么来的。 2、 布里渊区的高对称点 前面讲了一维周期条件下的布里渊区的能带是一条线，如果加上二维（X，Y）的周期 边界条件，这些能带又会变成什么样呢？答案是一个面，由原来的线组成一个面。因为在一 维情况下我们用一条能带来表示 k 矢量（对称操作）和能级的关系，可以用 E（k）来表示， 这构成第一布里渊区（即 k 的取值范围[0, π a ]）。对于二维周期体系，我们需要两个平移矢 量 kx 和 ky，所以能带可以用 E（kx，ky）来表示，当 kx＝0 时，变成 E（0，ky），得到一条 能带（线，y 方向上与一维周期情况的能带类似）；当 ky＝0 时，变成 E（kx，0），得到一条 能带（线）。由于 kx 和 ky 是矢量，它们可以组合成另外一个矢 量，这个矢量不是沿着 X 轴，也不是沿着 Y 轴，实际上沿着该 矢量仍是能够得到一个能带（线）的，这样的矢量有很多，所 有的这些能带（线）将构成一个面。如果我们在做能带结构图 的时候，将能带结构按照二维的面画出来是很困难的，而三维 的情况更加困难，因为对称操作有很多，k 矢量的取值有很多， 所以一个可行的办法就是让 k 的取值沿着一定的路径走，最后 回到起点。如右图（二维情况）。 这样，我们只要选择一些较高的对称点，就可以确定这个路径。比如二维的布里渊区是 一个面，这个面上每一点与原点（G 点或Γ点）的连线都构成一个 k 矢量，有一个 k 矢量就 有一个能级对应（E（k））。所以，二维的能带结构是这个布里渊区上的一个平面（面积）， 如上图，按照Γ——>X——>M——>Γ这个路径走，就可以得到一个可以大致反映布里渊 区上的能带平面的一个近似图，这就是二维的能带结构。具体的能带图的展开见下图。 展开以后得到 三维的能带展开见下图： 3
    前面讲了一维 H 原子链的能带结构，提到这个体系具有一个能带，并且是向上弯曲的 一个能带。这个能带是这样来的，H 原子链里面的基本单位（单体，单胞）是一个 H 原子， 每一个原子有一个原子轨道，即每一个基本单位有一个能级轨道，加上周期条件以后，这一 系列轨道能就变为一个能带了。假如，现在以两个 H 原子作为一个基本单位呢？能带结构 又是如何的呢？这就是能带重叠的问题 3、 能带的折叠 如上图，将 2 个氢原子作为一个基本单位，这时候能带结构是什么样子的呢？很容易理 解，根据前面的知识，单胞的原子轨道的数目决定了能带的数目，所以这样划分体系将有将 有两个能带。 但是这个体系与前面 1 个 H 原子周期链是一样的，只不过人为地进行了划分，能带结构 就变了吗？是的，能带确实变了，那么能带将怎样变化呢？下图分别是 1 个 H 原子为单胞 和 2 个 H 原子为单胞的能带结构。 第一个图可以清楚的看到，能带底部是成键的，能带的顶部是反键的，中间是非键的（成 键与反键相当），能带向上伸展（弯曲）。在第二个图，原来的中部的非键轨道分别变成了两 个能带的反键和成键轨道（相同颜色表示可以重叠成键，不同颜色表示中间有一个节点）。 实际上，这两个图是有关系的，能够反映相同的内容，首先，布里渊区从原来的[0, π a ]变为 [0, π a2 ]，这也是可以理解的，原来的能带长度要变成原来的一半（因为周期方向上的单胞 数减少一半，原来有 N 个单胞，以 2 个 H 原子为一个单胞后，单胞数变为一半，所以布里 4
    π a 渊区要减半）。其次，原来的能带在[0, ]展开，现在由于布里渊区减半，能带不能在[0, π a2 这个小区间画出来，所以能带结构将产生折叠，由原来的一个能带变为 2 个能带，并且是以 π k＝ a2 能带结构。如果我们将单胞取 3 个原子，或者取 4 个原子，体系的能带将如何变化？体系的 能带分别变为 3 条和 4 条能带，并且是 2 次或 3 次折叠原来的能带。 ]区间的能带折叠过去，所以就得到了 2H 原子为单胞的 为对称轴，将原来[ π a2 π ， a ] 另外，上面的例子我们也可以从另外一个角度考虑问题，即 2 个 H 原子组成一个 H2 分 子，形成成键分子轨道和反键分子轨道，把这两个分子轨道看成一个“原子”的两个“原子 轨道”，给这个“原子”加上周期条件以形成能带，这 样也得到 2 个能带。这种想法可以进行适当的扩充， 比如我们研究一个晶体，首先我们可以把单胞找出来， 然后将单胞的轨道能级画出来，考虑它们之间的成键， 最后得到一组分子轨道，以这组分子轨道为基础，给 它们加上周期条件，形成能带。这样的想法什么时候 有用呢?在组合成分子轨道以后，这些分子轨道并不是 不变的，有可能和相邻晶胞的分子轨道再次组合，这 种情况在过渡金属氧化物中非常普遍，所以在考虑成 键的时候除了单胞内成键情况以外，还需要考虑晶胞 间分子轨道的组合。 二次组合 二次组合 单胞1 单胞2 能带的折叠实际上是从不同的角度考虑问题而已，其实能带结构的本质还是一样的。 如果我们理解了这点，那么我们在分析能带的时候，就不会笨到建立一个很大的超胞去研究 其能带结构。所以我们要研究一个体系的能带结构时候，尽量选最小的单胞，以减少能带的 数目。 不幸的是，有时候我们往往要计算掺杂的情况而不得不建立一个很大的单胞（超胞）， 而掺杂的比例又与超胞的大小有关。如果要做 1/8 掺杂，那么起码要将 8 个晶胞做成一个单 胞（超胞），并将其中一个原子替换掉，从而实现掺杂。这样能带的数目将变为原来的 8 倍， 这样我们计算出来的能带将是一团曲线交缠在一起，再也无法分开。 大家可以试试建立一个超胞，然后计算能带，看看能带结构如何！ 所以能带结构的分析对于比较大的单胞（超胞）或者具有较多原子轨道的单胞将变得很 麻烦。而且 MS 中画出的能带结构很难看，如果我们要用 origin 作图的画，又要反复的 copy ＋paste 数据，所以建议在计算具有较多原子轨道（分子轨道）的体系时，尽量不用能带结 构分析问题（虽然它很有用^_^）。用态密度和 PDOS 就好多了。 另外，简单的提一下 Fermi 能级的概念，有很多书都将最高占据分子轨道（HOMO）的 顶部作为 Fermi 能级，所以我也采用这种观点，不知道大家是怎么理解的？ 下面我简单讲讲我做的体系的能带结构，具体做法参加我提供的动画演示。 4、3 维体系的能带——PbTiO3 的能带结构 要分析能带，首先要知道每个能带是属于那个轨道的，所以首先要画出单胞的轨道能级 图，下图是钛酸铅的轨道能级示意图，不是很准确（因为有一些轨道成键没有连线，仅给价 带和导带部分连线了）。 在轨道能级图里面先将各个原子的轨道能级标出来（横轴的能量是参考了 PDOS 加上的， 没有也没有关系^_^）。接着考虑成键，主要是中心 Ti 原子和 O 原子成键（模型参考下图）， 有 O 原子的 2p 轨道组成价带，2s 轨道的能量最低 Pb 的 4s 轨道比 O2p 轨道能量低，比 O2s 轨道高。另外 Ti 原子处于 TiO6 八面体中心，所以 3d 能级要分裂成 3 下（3t2g 态，3dxy,3dxz,3dyz 5
    2 轨道）和 2 上（eg 态，即 3dx 道在 Ti3d 轨道上面。 2,3dz -y 2 轨道），这些轨道构成导带。Pb 的 6d，Ti 的 4s，4p 轨 有了这些信息我们就可以绘制能带，并可以用不同的颜色表示不同轨道形成的能带，具 体的绘制过程见动画。 接下来看看能带能够说明什么问题。 第一点：O2s 能带有带宽，表明其参与成键（参与成 2 轨道，Ti4s，4pz 轨道，还有 Pb 原子轨道 键的有 Ti 的 3dz 的部分贡献，能带结构看不出来，但是态密度可以看出 来）。 第二点：Pb 的 6s 能带带宽比较大，说明 Pb6s 轨道参 与成键，由于 Pb 与 Ti 原子很远（3.45A）所以只能是与 O2p 轨道成键（能量相近，并且有带宽，从后面态密度分 析也可以得到同样的结论） 第三点：O2p 能带组成价带，体系中有 3 个 O 原子， 共有 9 条 O2p 能带，其中每 3 个是一组（G 点是 3 重简并 的）。 第四点：Ti3d 的 5 个能级分裂成 2 组，3 下 2 上，组成导带。 第五点：Pb 的 6p 和 6d 能带在 Ti 的 3 的能带上面，而且 Pb 的 6 的也要分裂，还有一 些能带图中未能表示出来，另外 Ti4s，4p 能带在最上面，且带宽比较大，说明它们参与了 与 O2p 轨道成键。 当然，能带结构还能给出很多信息，比如带隙等，由于水平有限，所以只能看出一些简 单的内容！希望对能带结构比较了解的朋友能够把这部分内容更加完善，大家共同探讨和学 习！ 下面我主要讲一下态密度的一些基本内容和初步的分析以及态密度的绘制。 第二部分：态密度 首先来看一下态密度的意义，前面提到当单胞（超胞）很大的时候，含有的原子轨道（分 子轨道）的数目就很多，采用能带分析的时候，必须处理很多能带。在单个分子中，我们可 以挑选出一个或一小组能决定分子的几何构型，反应性能等的轨道作为前线轨道或者价轨 道，但是，在多到几乎无法可数的晶体轨道（组成能带的能级）中，就没有可能找到某一个 能级来决定一种几何构型或反应性能。 举个例子来说，如果做表面成键或者吸附，首先要建立按照一定的晶面（如[110]面） 取向的表面构型，然后就是考虑吸附上去的原子对这个表面的影响情况，如果计算能带，当 6
    表面吸附的覆盖度很小时，这时候需要建的表面就很大，能带的数目自然就增加很大数目， 而影响到表面结构和性质的只要那么几条能带（吸附原子和被吸附原子的能带），如何从这 么多的能带中找到它们呢，这显然时吃力不讨好的事情（我觉得这时候用能带来解释不现 实），那么我们怎么考虑吸附质吸附上去以后，表面的结构和性质呢。我个人认为，只能靠 计算得到的态密度来分析了，特别时偏态密度（态密度投影或称 PDOS），比较被吸附原子 和吸附原子在吸附前或者吸附后的偏态密度应该能够很好的说明情况，而且如果能够加上布 居分析，局部的结构和性质应该可以弄清楚。比如做 TiO2[110]面吸附乙酸，我们可以计算 TiO2 晶体的态密度，计算 TiO2[110]，和吸附后的 TiO2[110]的态密度，这样，比较前两者， 就知道从晶体变到表面以后，吸附原子的成键变化情况，比较后两者，又可以知道吸附前和 吸附后，表面的结构怎么变化（成键等），性质发生什么变化。所以我个人认为，在计算表 面的结构性质的时候，应该更注意局部变化的情况。 那么态密度的物理意义是什么呢？ 1、 态密度的意义 态密度的物理意义应该是比较简单的。大家都知道，能带结构的纵坐标是能量，假如在 这个坐标轴上取ΔE 这一个很小能量范围（比如 0.005000～0.005001eV 这个范围），那么这 个能量间隔范围内又多少个能级，或者说又多少个原子轨道（分子轨道）呢？别忘了，能带 是怎么来的，是无数个能级“压缩”而成的，而且能带是量子化的，所以在这个能量范围必 然又一定数量的能级（轨道）存在。所以从这里开始，不再谈论单个的原子轨道或能级了， 因为这没有什么意义。而是我们将这一能量范围内的能级作为一组来考虑，所以态密度的概 念就得出来了，即 E＋dE 这个能量范围内的能级数，如果 E＋dE 这个能量范围内轨道（能级 数）越多越密集，态的密度越大，所以说态密度的概念是很贴切的。 而且要注意态密度是根据能带得来的，两者有一定的对应关系，比如在 E＋dE 这个能量 间隔没有能带，那么有态密度吗？这个答案是很显然的，没有能带，没有能级，哪能有态密 度呢？所以这时候态密度图在这个能量范围内将是 0。从这里可以得到一个结论，能带按照 纵坐标轴投影过去，就得到态密度，所以态密度为 0 的地方，能带图上一定没有能带经过。 在态密度中还有一个问题就是，有的峰很高，有的峰很低，这是为什么呢?为什么会产 生这种情况？这个很容易理解，比如一条水平的能带经过 E＋dE 这个区间，那么这个区间的 能级数是不是最大的呢？当然是，这个能带的所有能级都处于这个能量范围内，所以态的数 目最大，在态密度图中表现为一个很尖锐的峰。如果能带的带宽较大，这说明态密度图中它 很平缓，并且跨过的能量区间越大。一句话，能带越平，态密度峰越尖锐，能带越宽，态密 度越平缓，当然离域性越强了。 这里有两个问题：第一个问题：能带越平，是否成键越弱，或者不成键？即态密度峰越 尖锐，成键越弱或不成键呢？第二个问题：能带带宽越大，即态密度峰跨度越大越平缓，成 键是否越强？ 这两个问题，我查了一些书，但是没有答案，我个人的理解如下。对于第一个问题，能 带越平，不表示不成键或成键弱，为什么呢，比如两个原子轨道形成很强的σ键，那么根据 分子轨道理论，将形成一个成键分子轨道和一个反键分子轨道，成键越强，两者分离越大， 形成这两个分子轨道以后，在这个基础上在形成能带结构，也就是在 X，Y，Z 方向上加上周 期条件，假如在这 3 个周期方向单胞之间的距离比较远，那么两个分子轨道不能产生 2 次组 合，所以得到的能带只能是两条水平直线，所以我个人认为，能带平缓，或者态密度峰尖锐 不能说明这个轨道不成键或者成键比较弱。 第二个问题，我认为是这样的，带宽越大，成键越强，因为带宽越大，态密度峰跨度越 大，离域性越强，虽然不一定跟那个原子成键，但是其上面的电子离域了，肯定要成键，离 域越强，成键越强。 7
    上面两个问题是我自己思考的答案，当然不一定对，希望大家能够探讨探讨！ 接下来，想说说用态密度如何分析成键的问题。 2、 态密度与成键 下面的图是能级，能带以及态密度的关系，两个原子的原子轨道组合以后，得到两个分 子轨道，在周期边界条件下，这两个分子轨道形成两个能带，根据能带的宽度和斜率，可以 得到态密度的近似图。 上图右边的态密度图表示的是总的态密度，不是 PDOS，总态密度与 PDOS 的关系如何 呢？要解决这个问题，还得回到能带结构，在能带结构中，同一个能量 E 画一条水平横线， 与能带相交，交点有可以能很多个，并且有可能和几条能带相交，与这条直线相交的若干个 点对应于态密度图上能量为 E 的一个点，也就是说这个点包含了若干个能带的贡献，所以 得到总的态密度图，如果非要区分这些交点中属于那些轨道，则总态密度就得按照一定的原 则子划分到不同原子上，就得到了 PDOS。总之，总态密度是所有能带的贡献，而如果要对 这些贡献划分为某一个原子的贡献，则产生 PDOS。 再回到上面的图，上图中左边为分子轨道，这个分子轨道可以用波函数 c 1 1 χχψ 2 + = c 2 来描述，其中 1χ 和 2χ 表示两个原子轨道，那么它们组成的每一个分子轨道应该都有两个原 子轨道的贡献。但是对于成键轨道，主要以电负性大的原子的原子轨道为主（比如 O2p 轨 道），即成键分子轨道主要是电负性大的原子的原子轨道，当中掺入了部分另外一个原子轨 道的贡献；而反键分子轨道主要是由电负性小的原子的原子轨道构成，并且有电负性大的原 子轨道的贡献。也就是所这两个能带不是某一个原子轨道独自形成的的，每一个能带都是一 个原子轨道为基础，掺入了其他轨道的贡献，当然这个性质在能带结构中是无法反映的，你 不知道其他原子的原子轨道对某一个能带的贡献。那么，什么能够反映这个性质呢？答案是 态密度，更准确一些讲是 PDOS。下面看看如何用 PDOS 表示这个性质！ 如下图： 8
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料