第35卷 第1期河北工程大学学报（自然科学版）Vol.35 No.12018年3月Journal of Hebei University of Engineering(Natural Science Edition)Mar.2018GM(1，1)－星野法沉降预测模型研究与应用朱 婧1，2，洪宝宁1，2，刘 鑫2，3，常二阳1，2(1.河海大学 岩土力学与堤坝工程教育部重点实验室，江苏 南京 210098；2.河海大学 土木与交通学院，江苏 南京 210098；3.河海大学 隧道与地下工程研究所，江苏 南京 210098)摘要：围绕目前高速公路路基沉降预测精度不高，预测方法适用性不强等问题，基于组合预测理论，借助MATLAB计算软件，将基于灰色理论的GM(1，1)预测模型和星野法沉降预测模型线性组合，以组合预测误差的平方和最小为标准确定两种预测方法的权重系数，提出GM(1，1)－星野法组合预测模型。结合广东某高速公路施工期以及运营期路基实测沉降数据，GM(1，1)－星野法组合预测模型预测结果较两种方法单独预测结果具有更高的预测精度，工程适用性更强。关键词：GM(1，1)模型；星野法；MATLAB计算；组合模型；沉降预测中图法分类号：TU470.2 文献标识码：AResearch and application of GM (1，1) - Hoshino Nori settlement prediction model ZHU Qian1，2，HONG Baoning1，2，LIU Xin2，3，CHANG Eryang1，2 (1.Key Laboratory of geotechnical mechanics and embankment engineering of Ministry of education，Hohai University，Nanjing 210098；2.School of civil engineering and transportation，Hohai University，Nanjing 210098；3.Institute of tunnel and underground engineering，Hohai University，Nanjing 210098)Absract：The prediction accuracy of subgrade settlement is not high and the applicability of prediction method is not strong. Based on the combination forecast theory，with the help of MATLAB software，GM(1，1)—Hoshino Nori combination forecasting model is proposed. This model is based on the grey theory GM(1，1) forecasting model linear combination model and Hoshino Nori settlement prediction，taking the combination forecasting error square as standard to determine the weight coefficients of two kinds of prediction methods and minimum standards. With the Guangdong highway construction period and operation period of subgrade settlement data，GM(1，1)—Hoshino Nori combination forecasting model prediction results are better than the two methods separately predicted results. The present method has higher prediction precision，stronger engineering application. Key words：GM(1，1) model；Hushino method；MATLAB calculation；composite model；settlement prediction收稿日期：2017-09-06基金项目：国家自然科学基金青年基金(51609071)；江苏省自然科学基金青年基金(BK20140848)；广东省交通运输厅科技项目(科技-2015-02-013)作者简介：朱婧(1992-)，女，江苏扬州人，硕士，从事地基处理与地下工程方面研究。文章编号：1673-9469（2018）01-0062-04doi：10.3969/j.issn.1673-9469.2018.01.014近年来高速公路建设存在质量控制方面一些问题。其中高速公路路基沉降对路面平整性以及路面结构的稳定性影响巨大。因此有必要通过分析现场实测沉降资料，预测后期沉降，在施工过程中对路基沉降变形进行动态设计和施工控制[1]。GM(1，1)模型和星野法预测沉降被广泛应用到路基最终沉降的预测。张大海等[1]分析GM(1，1)预测模型存在的理论不足和缺陷，同时提出了新的预测计算公式，提高了预测精度。高蔚[2]将灰色预测模型与马尔可夫预测方法优化组合，提高了GM(1，1)模型的预测精度。GM(1，1)模型也被大量用于路基等建筑物沉降预测方面[3-6]。李爽等[7]将星野法预测模型应用到发电厂地基沉降预测中。部分研究者还根据组合方法理论用多种模型组成新的模型，获得一定中国煤炭期刊网 www.chinacaj.net

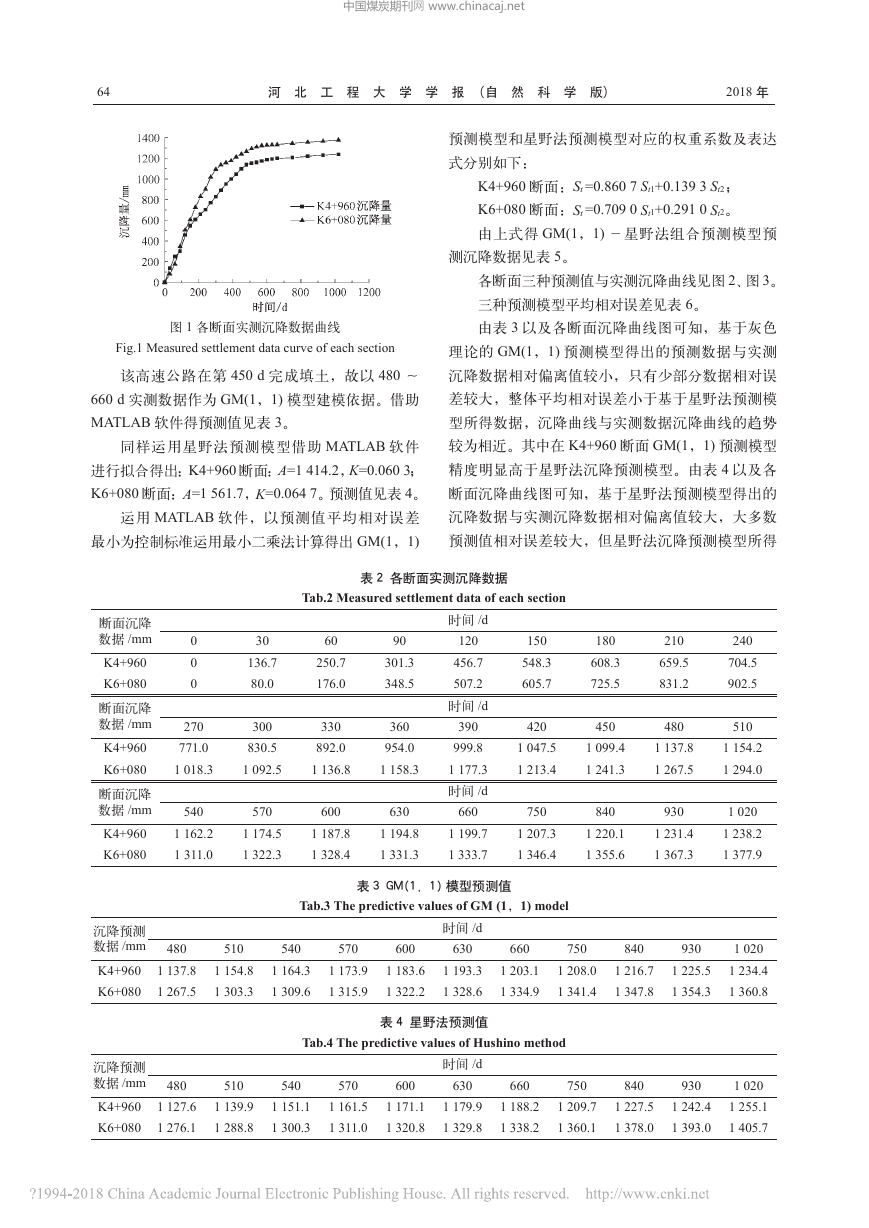
第4期63表1 各断面软土地基状况Tab.1 The condition of soft soil foundation in every section的成果。根据Logistic曲线和Compertz曲线的共性和个性，赵明华等[8]建立了最优加权几何平均组合沉降预测模型。欧阳炼[9]提出了GM(1，1)-Logistic组合路基沉降预测模型。本文以广东某高速公路路基沉降实测数据为基础，运用GM(1，1)、星野法组合预测模型对未来沉降进行预测，同时与单个预测模型预测结果进行对比分析。1 基本原理1.1 GM(1，1)预测模型灰色系统理论是20世纪80年代由我国邓聚龙教授提出的一种数学方法，可用来解决小样本的信息不完备系统的复杂问题，在岩土工程中得到了广泛的应用[9]。其建模的实质是对原始数据先进行一次累加生成，使生成的数据序列呈现一定规律，而后通过建立一阶微分方程模型，求得拟合曲线，用以对系统进行预测。具体过程如下：(1)原始数据序列x(0)={x(0)(1)，x(0)(2)，…，x(0)(n)}(2)累加生成序列x(1)={x(1)(1)，x(1)(2)，…，x(1)(n)}式中x(1)(k)=x(0)(i)，k=1，2，…，n。(3)其参数求解公式(4)解的离散形式x＾(1)(k+1)=(x(0)(1) － u—a )e－ak+ u—a，k=1，2，…，n(5)还原原始数据x＾(0) ={x＾(0)(2)，x＾(0)(3)，…，x＾(0)(n)式中x＾(0)(k)=x＾(1)(k)－x＾(1)(k－1)。1.2 星野法预测模型基于太沙基固结理论，在固结度U＜60%时，固结度U与时间平方根成正比。星野法通过对现场沉降值的研究，证明了总沉降(包括剪切应变的沉降在内)是与时间平方根成正比。其计算公式为总沉降为式中：S0为瞬时沉降量；S为经过t时间后的沉降量；St为最终沉降量；t0为初始瞬时沉降经过的时间；t为沉降经过的时间；A和K为待定系数。令∆S =St－S0，∆t =t－t0，变换上式得：令，，，x=∆t，则上式变换为y=Bx+D线性方程，由曲线拟合求出B和D，进而求出最终沉降量。1.3 GM(1，1)－星野法预测模型GM(1，1)预测模型和星野法沉降预测模型在依据实际沉降数据对未来沉降进行预测均具有自身的优势和不足，如何把这两者结合起来，取两者长处，组成新的预测模型是研究的重点。本文通过已知沉降数据，分别用GM(1，1)和星野法沉降预测模型对未来沉降进行预测。所得的结果以预测结果误差平方和最小为控制标准，建立线性曲线关系，由线性关系赋予两种方法不同的权重以达到提高预测精度的目的。计算公式为St = w1St1 + w2St2w1+ w2 = 1其中w1，w2分别为GM(1，1)预测模型和星野法沉降预测模型对应的权重系数。2 工程实例分析广东某高速公路A标的软基路段位于山丘与平原过渡区域，鱼塘密集分布，种植地和居住区集中，水网沟渠纵横，而且路堤填筑比较高(普遍大于8.0 m)，软土层厚，上覆土层薄甚至无覆土层，现场排水困难。本文分析了K4+960、K6+080两个断面的实测沉降数据，两个断面的软基及路堤填高情况见表1。两个断面沉降数据见表2，沉降曲线见图1。断面上覆土层厚/m软土层厚/m处理方式/m填土高度/mK4+9606.012.0塑料排水板10.4K6+080611.2塑料排水板8.1朱婧等：GM(1，1)－星野法沉降预测模型研究与应用中国煤炭期刊网 www.chinacaj.net

河北工程大学学报（自然科学版）642018年表2 各断面实测沉降数据Tab.2 Measured settlement data of each section断面沉降数据/mm时间/d0306090120150180210240K4+9600136.7250.7301.3456.7548.3608.3659.5704.5K6+080080.0176.0348.5507.2605.7725.5831.2902.5断面沉降数据/mm时间/d270300330360390420450480510K4+960771.0830.5892.0954.0999.81 047.51 099.41 137.81 154.2K6+0801 018.31 092.51 136.81 158.31 177.31 213.41 241.31 267.51 294.0断面沉降数据/mm时间/d5405706006306607508409301 020K4+9601 162.21 174.51 187.81 194.81 199.71 207.31 220.11 231.41 238.2K6+0801 311.01 322.31 328.41 331.31 333.71 346.41 355.61 367.31 377.9图1 各断面实测沉降数据曲线Fig.1 Measured settlement data curve of each section表3 GM(1，1)模型预测值Tab.3 The predictive values of GM (1，1) model沉降预测数据/mm时间/d4805105405706006306607508409301 020K4+9601 137.81 154.81 164.31 173.91 183.61 193.31 203.11 208.01 216.71 225.51 234.4K6+0801 267.51 303.31 309.61 315.91 322.21 328.61 334.91 341.41 347.81 354.31 360.8表4 星野法预测值Tab.4 The predictive values of Hushino method沉降预测数据/mm时间/d4805105405706006306607508409301 020K4+9601 127.61 139.91 151.11 161.51 171.11 179.91 188.21 209.71 227.51 242.41 255.1K6+0801 276.11 288.81 300.31 311.01 320.81 329.81 338.21 360.11 378.01 393.01 405.7预测模型和星野法预测模型对应的权重系数及表达式分别如下：K4+960断面：St =0.860 7 St1+0.139 3 St2；K6+080断面：St =0.709 0 St1+0.291 0 St2。由上式得GM(1，1)－星野法组合预测模型预测沉降数据见表5。各断面三种预测值与实测沉降曲线见图2、图3。三种预测模型平均相对误差见表6。由表3以及各断面沉降曲线图可知，基于灰色理论的GM(1，1)预测模型得出的预测数据与实测沉降数据相对偏离值较小，只有少部分数据相对误差较大，整体平均相对误差小于基于星野法预测模型所得数据，沉降曲线与实测数据沉降曲线的趋势较为相近。其中在K4+960断面GM(1，1)预测模型精度明显高于星野法沉降预测模型。由表4以及各断面沉降曲线图可知，基于星野法预测模型得出的沉降数据与实测沉降数据相对偏离值较大，大多数预测值相对误差较大，但星野法沉降预测模型所得该高速公路在第450 d完成填土，故以480 ～660 d实测数据作为GM(1，1)模型建模依据。借助MATLAB软件得预测值见表3。同样运用星野法预测模型借助MATLAB软件进行拟合得出：K4+960断面：A=1 414.2，K=0.060 3； K6+080断面：A=1 561.7，K=0.064 7。预测值见表4。运用MATLAB软件，以预测值平均相对误差最小为控制标准运用最小二乘法计算得出GM(1，1)中国煤炭期刊网 www.chinacaj.net

第4期65沉降曲线相对较平滑，同时，时间越久，预测沉降值与实际沉降值相对误差越大，并且向偏大的方向偏离，更偏向于保守预测。从K4+960、K6+080两个断面可知，GM(1，1)-星野法组合预测模型的平均相对误差较小，预测精度最高，星野法预测模型的相对误差较大，整体精度较低，基于灰色理论的GM(1，1)预测模型相对误差居中，预测精度居中。因此，为了掌握路基沉降的变化趋势，获得更精确的沉降预测值，GM(1，1)-星野法组合预测模型具有更强的适用性。3 结语1)基于灰色理论的GM(1，1)预测模型运用MATLAB软件根据实测值可以对未来沉降值进行预测，且预测精度相对较高。2)利用星野法预测模型所得预测沉降曲线较平滑，且随时间推移预测结果趋向于偏大，预测结果偏于保守，预测精度一般。3)通过在实际工程三个断面的应用，GM(1，1)-星野法组合预测模型得到的沉降曲线与实际沉降曲线更为接近，相较于两种单独的预测模型，组合法预测模型相对误差较小，具有更高的预测精度。因此在实际工程应用中，为了获得更高的预测精度，GM(1，1)-星野法组合预测模型具有更高的适用性。参考文献：[1]张大海，江世芳，史开泉.灰色预测公式的理论缺陷及改进[J].系统工程理论与实践，2002(8)：140-142. [2]高 蔚.基于Markov理论的改进灰色GM(1，1)预测模型研究[J].计算机工程与科学，2011，33(2)：159-163. [3]薛 祥，宋连亮，贾 亮，等.高速公路软土路基工后沉降预测的新方法[J].岩土工程学报，2011，33(Z1)：132-137.[4]高庆丰.软土地基路堤工后沉降计算与预测[D].杭州：浙江大学，2003.[5]陈 青.在高层建筑沉降预测中组合模型的应用研究[D].昆明：昆明理工大学，2011.[6]刘学文，虎旭林，丁丽宏.灰色系统与时序组合模型在高层建筑沉降预测中的应用[J].宁夏大学学报：自然版，2003，24(1)：60-62.[7]李 爽，郭晓昕，王文国，等.星野法在某发电厂地基沉降预测中的应用[J].水利科技与经济，2015(8)：99-100.[8]赵明华，龙 照，邹新军.基于Logistic曲线和Gompertz曲线的最优组合沉降预测模型及其应用[J].公路交通科技，2007，24(12)：1-5.[9]李恒凯，刘传立.基于灰色理论的变形智能预测模型库研究[J].岩土力学，2011，32(10)：3119-3124.(责任编辑 王利君)表5 组合法沉降预测值Tab.4 The predictive values of composite model沉降预测数据/mm时间/d4805105405706006306607508409301 020K4+9601 136.41 152.71 162.51 172.21 181.91 191.41 201.01 208.21 218.21 227.91 237.3K6+0801 270.01 299.11 306.91 314.51 321.81 328.91 335.91 346.81 356.61 365.61 373.9图2 K4+960沉降曲线Fig 2 Settlement curve of K4+960图3 K6+080沉降曲线Fig 3 Settlement curve of K6+080表6 三种预测模型平均相对误差断面平均相对误差/%GM(1，1)模型法星野法组合法K4+9600.1970.9890.178K6+0800.4730.9400.260朱婧等：GM(1，1)－星野法沉降预测模型研究与应用中国煤炭期刊网 www.chinacaj.net