第1页 / 共27页
第2页 / 共27页
第3页 / 共27页
第4页 / 共27页
第5页 / 共27页
第6页 / 共27页
第7页 / 共27页
第8页 / 共27页
编译原理第三版课后习题及答案.doc
P36-6
P36-7
P36-8
P36-9
P36-10
P36-11
P64–7
P64–8
P64–12
P64–14
P81–1
P81–2
P81–3
P133–1
P133–2
P133–3
P134–5
P164–5
P164–7
P217–1
P217–3
P218–4
P218–5
P218–6
P218–7
P219–12
P270–9
第二章
P36-6
(1)
L G(
)1 是 0~9 组成的数字串
(2)
最左推导:
N
ND
ND
N
N
ND
最右推导:
ND
N
ND
N
ND
N
P36-7
NDDD
34
D
DDD
NDD
DD
NDD
3
7
8
ND
4
D
ND
N
N
N
7
4
8
N
34
N
DDDD
0
DDD
01
DD
012
D
0127
5
DD
56
D
568
27
ND
27
N
127
D
127
0127
68
D
68
568
G(S)
O
N
D
S
A
|
|
|
N
1 3 5 7 9
|
|
2 4 6 8
|
|
|
O
|
0
|
O AO
|
AD N
P36-8
/
文法：
|
|
T E T E T
E
| * |
F T F T F
T
(
)|
E i
F
最左推导:
*
i T F
E T
E
)
*(
*
i E T
E
T
T F
)
*(
i T
i
i
F T
*
F F
)
i F
i T
*(
i E
)
i
T T
*(
*
i F
*(
i
i
*
i F F
i
)
*
i F
i
)
*(
T T
*
i
i
i
*(
i F T
)
最右推导:
*
E T F
E T
E
*
F F
T
E
*(
*(
F T i
F
F i
*
F T
)
*
E T i
)
*(
E
F
*(
)
F i
*(
i
i
*
E F i
E T
F
*(
)
i
)
)
i
*
i
F i
*(
)
E i
*
T i
i
)
E i
F
E F
*
i
*(
F
i
i
*
i
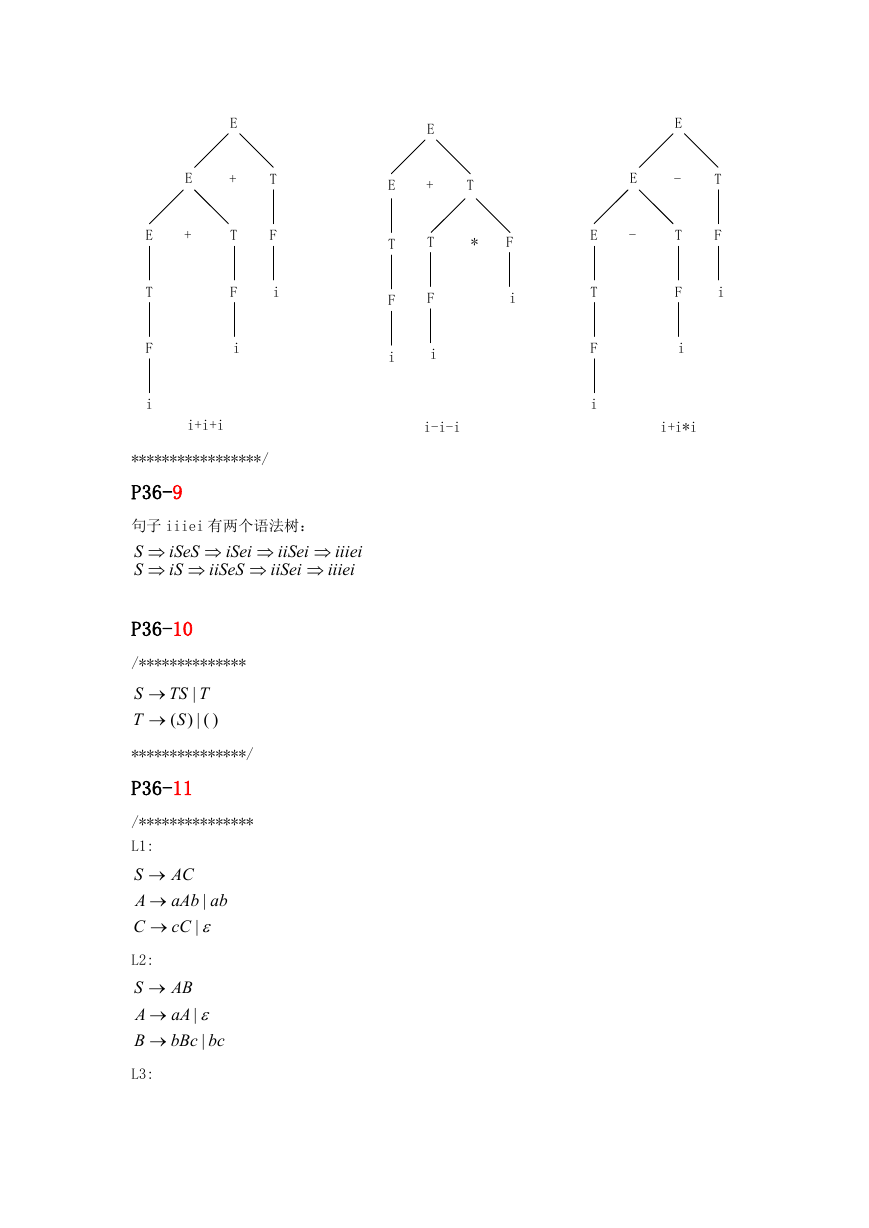
语法树：/********************************
E
+
T
F
i
T
F
i
E
+
E
T
F
i
E
+
T
F
i
E
T
F
i
T
*
F
i
E
-
T
F
i
T
F
i
E
-
E
T
F
i
i+i+i
i-i-i
i+i*i
*****************/
P36-9
句子 iiiei 有两个语法树：
S
iiSei
iiSei
S
iSeS
iS
iSei
iiSeS
iiiei
iiiei
P36-10
/**************
S
T
T
TS
) (|)(
S
|
***************/
P36-11
/***************
L1:
S
A
C
L2:
S
A
B
L3:
AC
aAb
cC
|
|
ab
AB
|
aA
bBc
|
bc
S
A
B
AB
aAb
aBb
|
|
L4:
S
A
B
|
BA
|10
A
|01
B
A
***************/
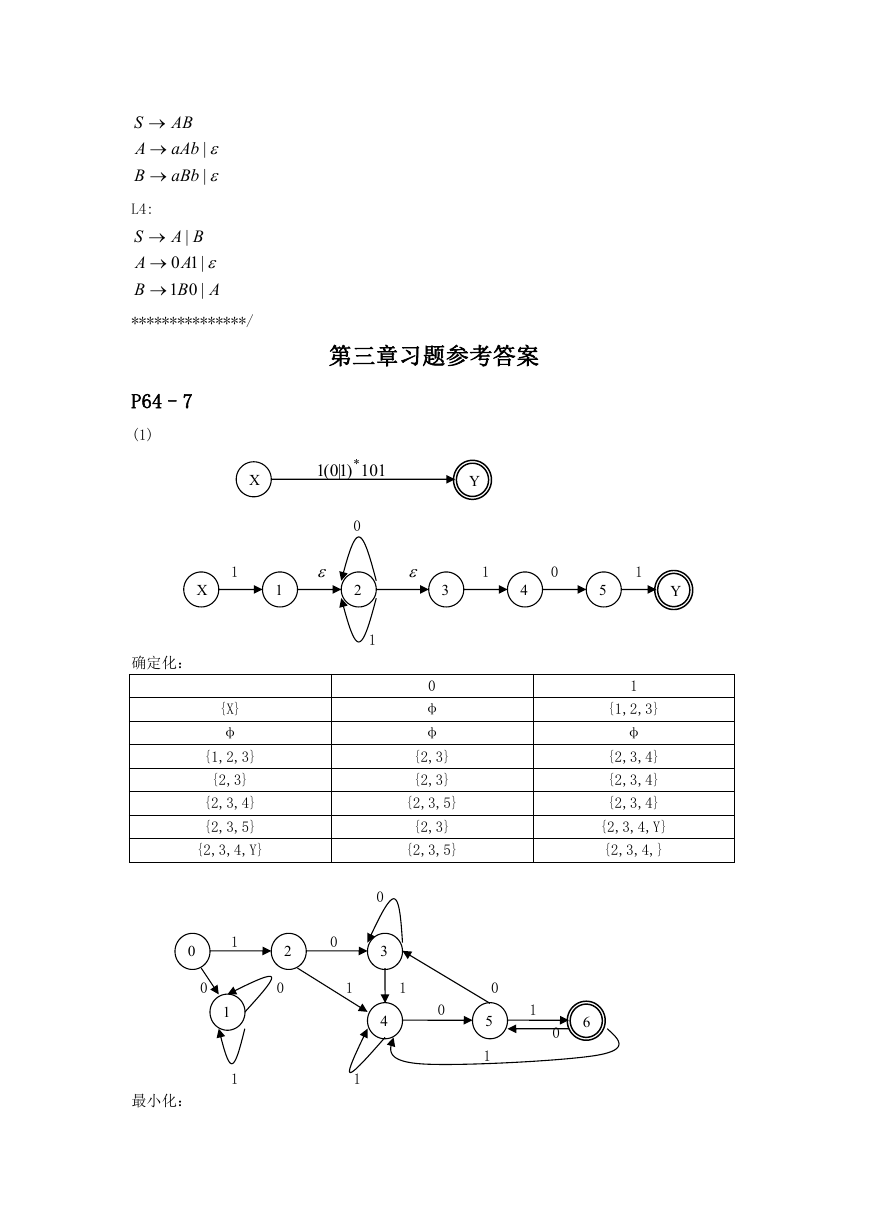
P64–7
(1)
第三章习题参考答案
X
( | )*
1 01 101
Y
1
X
1
确定化：
{X}
φ
{1,2,3}
{2,3}
{2,3,4}
{2,3,5}
{2,3,4,Y}
0
0
1
1
1
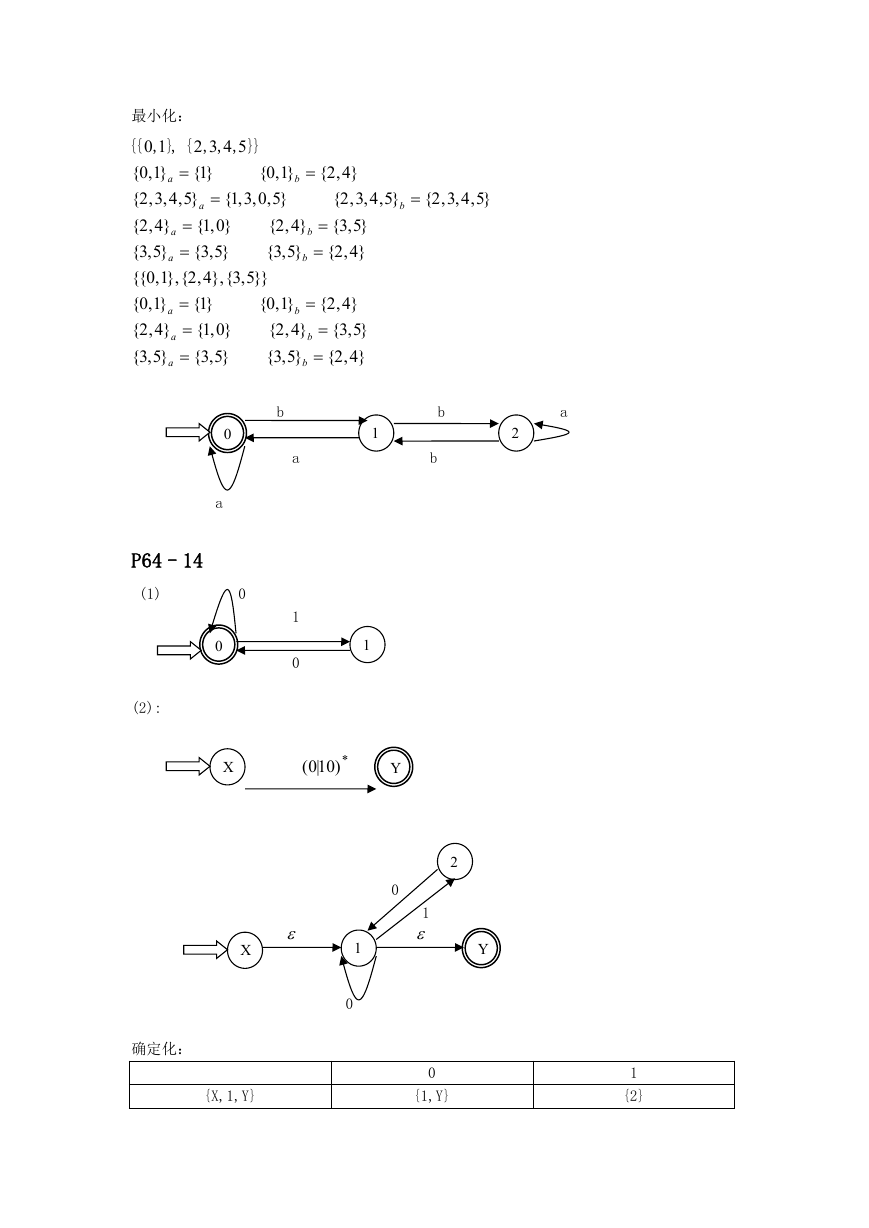
最小化：
2
0
0
1
0
2
1
0
3
4
1
3
1
0
1
4
5
Y
0
φ
φ
{2,3}
{2,3}
{2,3,5}
{2,3}
{2,3,5}
1
{1,2,3}
φ
{2,3,4}
{2,3,4}
{2,3,4}
{2,3,4,Y}
{2,3,4,}
1
0
0
5
1
1
6
0
, }
{ , ,
0 1 2 3 4 5
1
, ,
{ ,
, }
1 2 4 6
,
0
5
, },{ }
6
, ,
{ , ,
0 1 2 3 4 5
{ , , }
{ , ,
, ,
, }
0 1 2 3 4 5
1 3 5
, , },{ },{ }
{ , ,
0 1 2 3 4
6
, , }
{ , ,
{ , , }
0 1 2 3 4
1 3 5
0
4
5
, },{ },{ },{ }
{ , ,
0 1 2 3
6
{ , ,
0 1 2 3
3
, }
, }
{ , ,
{ ,
1
0 1 2 3
}
0
1
6
2 3 4
5
0 1
{ , },{ , }{ },{ },{ }
1 2
{ , }
1
{ }
0 1
{ , }
0 1
{ , }
0
1
2 3
4
2 3
3
{ }
{ , }
{ }
{ , }
0
1
5
1
6
{ },{ },{ , },{ },{ },{ }
0
2 3
4
1 2 4
{ ,
, }
0
2
3
1
0
0
1
0
1
1
1
0
0
4
1
1
5
0
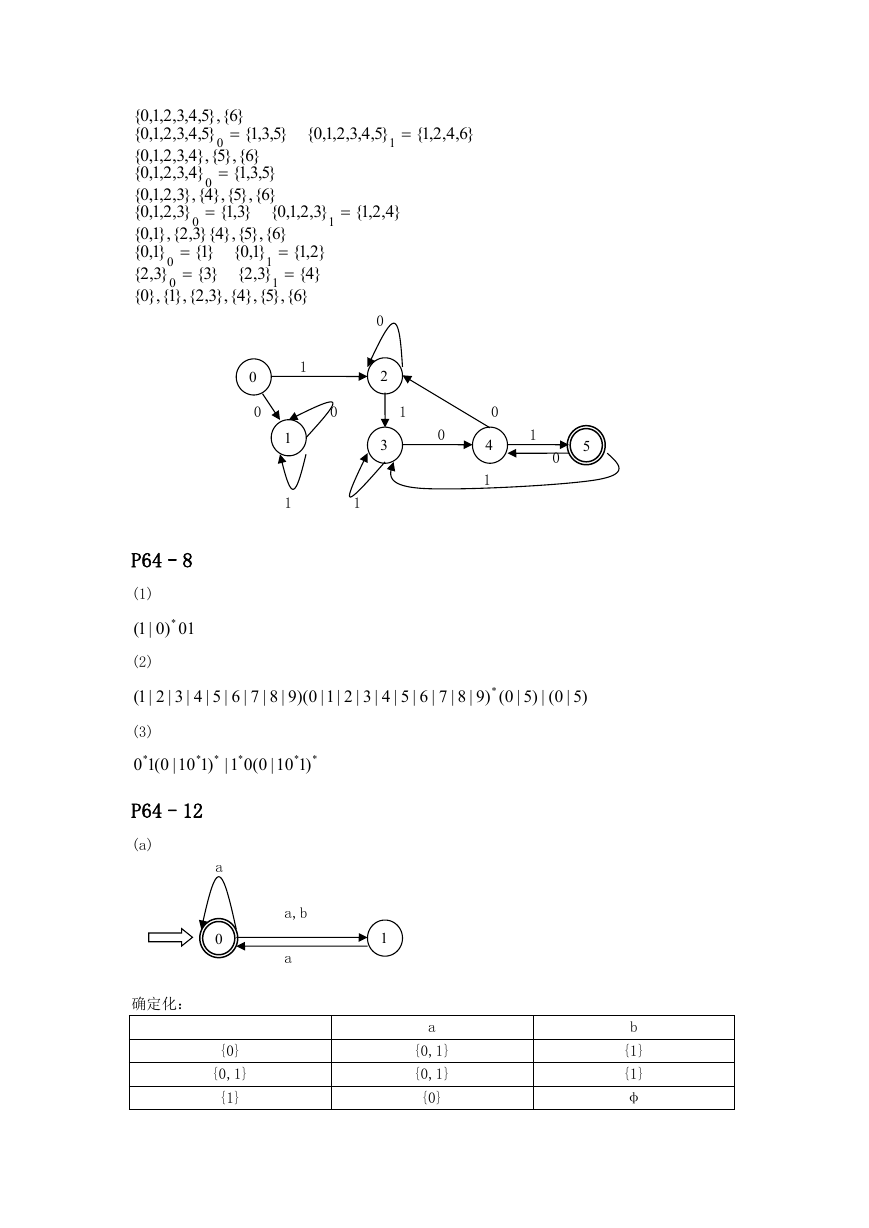
P64–8
(1)
01)0|1(
*
(2)
)5|0(|)5|0()9|8|7|6|5|4|3|2|1|0)(9|8|7|6|5|4|3|2|1(
*
(3)
*
)110|0(01|)110|0(10
*
*
*
*
*
P64–12
(a)
确定化：
a
0
{0}
{0,1}
{1}
a,b
a
1
a
{0,1}
{0,1}
{0}
b
{1}
{1}
φ
φ
b
2
2
3
3
φ
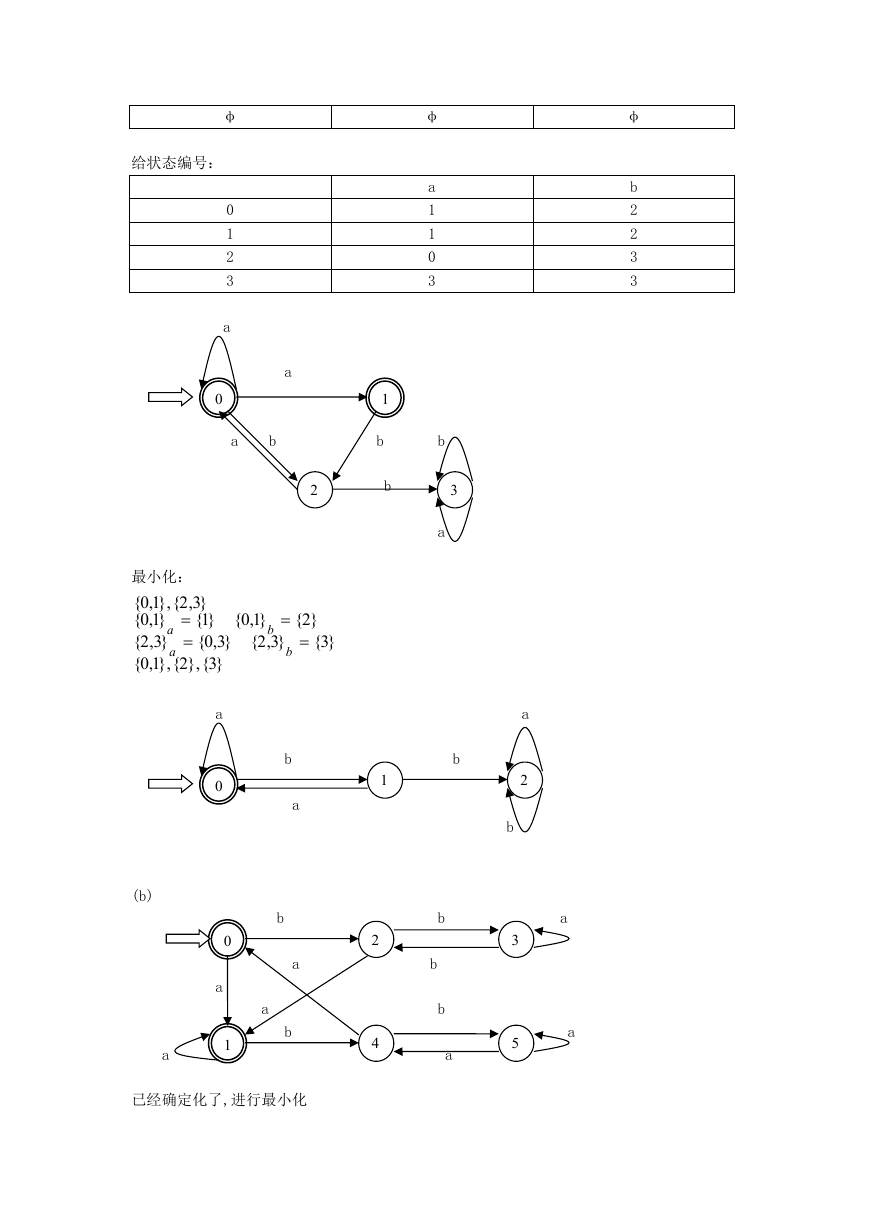
给状态编号：
0
1
2
3
a
0
a
b
a
2
1
b
b
φ
a
1
1
0
3
b
a
3
最小化：
2 3
{ , },{ , }
0 1
{ , }
0 1
{ }
1
a
{ , }
{ , }
2 3
0 3
a
2
{ , },{ },{ }
0 1
3
b
{ , }
0 1
b
{ , }
2 3
{ }
2
{ }
3
a
0
a
0
1
b
a
b
a
a
b
(b)
a
已经确定化了,进行最小化
a
2
b
3
5
a
a
b
1
2
4
b
b
b
a
最小化：
a
a
0 1
2 3 4 5
{{ , }, { , , , }}
0 1
{ , }
2 4
{ , }
0 1
{ , }
1
{ }
b
2 3 4 5
{ ,
, }
,
2 3 4 5
,
{ ,
, }
1 3 0 5
, }
{ ,
,
b
a
2 4
{ , }
1 0
3 5
{ , }
2 4
{ , }
{ , }
b
3 5
{ , }
2 4
{ , }
3 5
{ , }
3 5
{ , }
a
b
2 4
0 1
{{ , },{ , },{ , }}
3 5
1
0 1
{ , }
{ }
a
2 4
{ , }
{ , }
1 0
{ , }
{ , }
3 5
3 5
2 4
{ , }
{ , }
3 5
{ , }
2 4
0 1
{ , }
b
{ , }
2 4
b
{ , }
3 5
b
a
a
2 3 4 5
{ ,
, }
,
b
0
a
1
0
a
0
0
P64–14
(1)
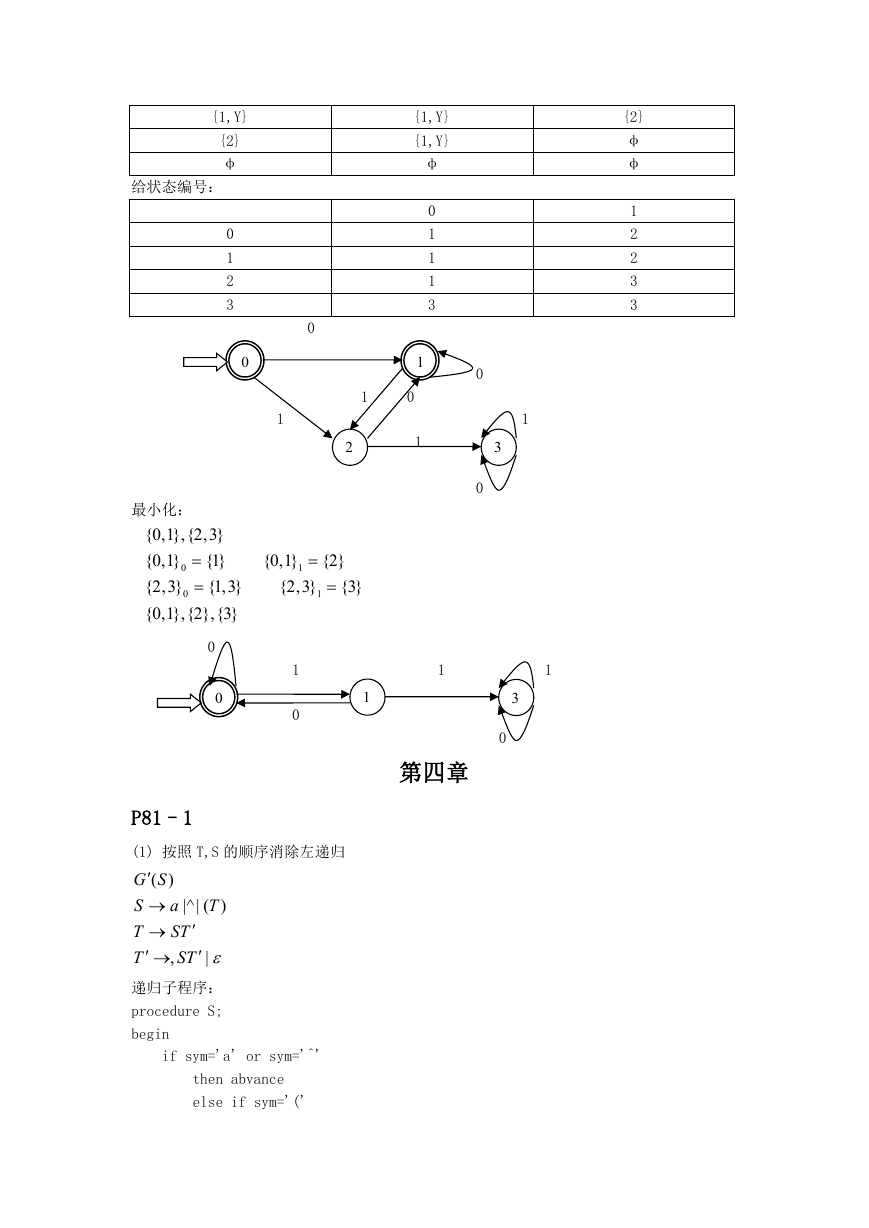
(2):
X
)*
( |
010
X
1
0
1
b
b
a
2
1
Y
0
2
1
Y
确定化：
{X,1,Y}
0
{1,Y}
1
{2}
{2}
φ
φ
1
2
2
3
3
{1,Y}
{2}
φ
给状态编号：
{1,Y}
{1,Y}
φ
0
1
2
3
0
0
1
1
1
3
1
1
0
1
0
1
2
0
0
1
3
最小化：
2 3
{ , },{ , }
0 1
{ }
{ , }
0 1
1
0
{ , }
{ , }
2 3
1 3
2
{ , },{ },{ }
0 1
3
0
{ , }
0 1
1
{ , }
2 3
1
{ }
2
{ }
3
0
0
1
0
1
1
1
3
0
第四章
P81–1
)(|
T
(1) 按照 T,S 的顺序消除左递归
)(
SG
|^
S
a
T
TS
|
,
TS
T
递归子程序：
procedure S;
begin
if sym='a' or sym='^'
then abvance
else if sym='('
then begin
advance;T;
if sym=')' then advance;
else error;
end
else error
end;
procedure T;
begin
S; T
end;
procedure
begin
T ;
if sym=','
then begin
advance;
S; T
end
end;
其中:
sym:是输入串指针 IP 所指的符号
advance:是把 IP 调至下一个输入符号
error:是出错诊察程序
(2)
FIRST(S)={a,^,(}
FIRST(T)={a,^,(}
FIRST( T )={,,}
FOLLOW(S)={),,,#}
FOLLOW(T)={)}
FOLLOW( T )={)}
预测分析表
a
S
a
ST
T
^
S ^
ST
T
(
S
T
T (
)
ST
)
,
#
T
T
ST,
S
T
T
是 LL(1)文法
P81–2
文法：
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
