探测器接近段自主导航的改进UD-EKF滤波算法应用.pdf-资料库

中国科技论文在线 http://www.paper.edu.cn 探测器接近段自主导航的改进 UD-EKF 滤波算法应用翟伟青岛科技大学自动化与电子工程学院自主导航与智能控制研究所，山东青岛（266042）摘要：本文针对深空探测任务对探测器实时性要求较高，然而星载计算机计算能力有限的问题，根据接近段轨道动力学模型建立状态方程，通过星光仰角建立观测模型,将一种改进的 UD-EKF 滤波算法应用到接近段自主导航方案中。通过协方差分解算法和多个观测量的逐步更新，避免繁杂的矩阵求导求逆运算，缩短了运行时间。通过计算机仿真证实了其可行性。关键词：自主导航；UD 分解；EKF 滤波；星光仰角中图分类号：V448.2 文献标识码：A 0 引言深空探测任务对探测器状态估计的实时性具有较高要求，然而星载计算机信息处理能力有限，这就需要在保证精度的情况下尽量减少估计时间。探测器轨道动力学模型的非线性导致经典的卡尔曼滤波在很多时候无法正常使用，基于泰勒展开的扩展卡尔曼滤波 EKF(Extended Kalman Filter)和 UKF1(Unscented Kalman Filter)就成为导航系统常用的滤波方法，但是它们在处理较为严重的非线性非高斯问题的时候，滤波性能大大降低[3]。就扩展卡尔曼滤波而言，虽然能够处理非线性问题，但是一方面存在较大的舍入误差，另一方面扩展卡尔曼滤波需要进行大量的矩阵运算，包括矩阵求导、矩阵求逆等浪费时间导致实时性大大降低。 UD 协方差分解的扩展卡尔曼滤波算法（UD-EKF）通过 UD 分解算法和多个观测量逐个更新，减少舍入误差的影响以及计算量和数据存储量[1]。对一步预测误差方差阵进行 UD 分解，分解为上三角矩阵和对角矩阵相乘的形式，再加以迭代运算，保证了协方差矩阵的非负定性和对称性，避免了繁杂的雅可比矩阵求导、矩阵求逆，节约了状态估计的时间。但是, UD 分解过程中受处理器字长的限制，矩阵中的某个元素小于处理器的最小精度值时便被置零[2]，导致误差的积累影响估计精度甚至有可能影响系统的稳定性。改进的 UD-EKF 通过有效分析编排状态量的方法克服 UD 分解算法的局限性[2]，在一定程度上解决误差积累的问题，达到了较好的估计结果。本文在详细介绍 UD-EKF 滤波及其改进方法后，将探测器接近段轨道动力学模型加以简化，结合恒星仰角观测模型将改进的 UD-EKF 滤波应用到探测器自主光学导航里面去，在保证必要的精度的前提下，提高了状态估计的速度。 1 UD-EKF 及其改进 1.1 UD 分解的 EKF 滤波算法 UD-EKF 滤波算法的实质是把协方差矩阵 KP 分解成的形式。其中 D 为对角矩阵，U 为上三角矩阵。也就是说 UD-EKF 滤波并不直接求解协方差矩阵 kP 而是求解其对应的U 阵和 D 阵来保证滤波过程中的 ( ) kP UDU kP + 和 ( ) kP − 的非负定性。 = T UD-EKF 公式的获得是对 EKF 的五个重要公式进行必要的变换，基本过程如下所示：第一步，状态量的一步预测： -1-

中国科技论文在线 http://www.paper.edu.cn ∧ X = Φ − 1 − k k , k k , 第二步，误差协方差矩阵的一步预测： P k = Φ k k , 对误差协方差矩阵进行 UD 分解： U = P k k , P k k , k k , − − − 1 1 1 X k 1 − 1 （1-1） T Φ 1 − k k , − 1 + Q k − 1 （1-2） D k k , − 1 U 1 T k k , − 1 − （1-3）具体分解方法如下：首先，对于 D 阵有： D n n , = P n n , D j , = j P j , j 其次，对于 U 阵有： n − ∑ k j 1 = + D U k k , 2 j k , （1-4） U i n , U i , j i n n n − 1, 2, ,1 = − P ⎧ i n , i ⎪= ⎨ P n n , ⎪ = 1 ⎩ 0 > ⎧ ⎪ ⎪ 1 ⎪ = = ⎨ ⎪ ⎪ ⎪ ⎩ ∑ j 1 = + D j D U U < P i k k , − j k , i k , i i i n k j j , , （1-5） j j j （1-6）第三步，滤波增益矩阵的一步预测：取 T k k , − k k , U F D k 1 F G U k 1 − S H G R + k k k = = = k k , k k H T k 1 − （1-7） ( H H P k k 1 D U T 1 k k , k k , − 1 T k R + k − H H U H ( T k k k k , / k 1 − 1 − ) D k k , − 1 U 1 T k k , − H T k 1 − + R k ) − 1 （1-8） − 1 + ∧ K Z H X − ( K K K K K / − ) 1 K K / （1-9）则一步预测的滤波增益矩阵： T k − k − 1 1 − k / k K = = = P k U k k , G S k 第四步，状态量更新： ∧ X ∧ X ∧ X = K + 第五步，误差协方差矩阵更新： = K K − 1 / G S K ∧ Z H X K − K 1 − K ( K K / − ) 1 -2-

中国科技论文在线 http://www.paper.edu.cn 1 − [ k k , K K P K I K H P ] − = K K , D G S U 1 − = [Ι − Η ] k k K , Κ K U D U U T = − k k k k 1 1 , , k k 1 , − D F S F U U ) ( T 1 − = K K 1 K 1.2 UD-EKF 滤波算法的改进 k k , k k , k k , − − − − − 1 1 1 − − U T 1 k k , D 1 − k k , T k k , 1 − U 1 T k k , − 1 − 1 H S H U K k k 1 , − K − K D k k , − 1 U 1 T k k , − 1 − （1-10）具体方法：选好状态量，在进行系统仿真的时候先进性必要的分析，把驱动噪声方差较小（只考虑误差值不考虑单位）的状态量放在前面，避免误差积累导致的绝对值小于处理器可执行最高精度的最小值而被错误置零[2]。 2 改进的 UD-EKF 在接近段自主导航中的应用 2.1 系统模型 2.1.1 系统状态方程探测器接近目标天体时，由于距离目标天体较近，虽然仍旧受到太阳引力的作用，但是其主要的摄动力为目标天体的万有引力和太阳光压。因此建立在 2000 的接近段轨道动力学方程形式如下【4】： • r • v T a [ µ a = − v r r + = + − − + ] J r r r 3 r r t r 3 t AG mr 3 k m µ s r 3 （2-1）日心黄道坐标系中其中 sµ 为太阳引力常数； aµ 为目标天体引力常数； A 为探测器截面积，m 为探测器质量， → G 为太阳光压系数。T 为推力矢量；a 器在 2000 J 日心黄道坐标系中的位置矢量和速度矢量，并且 r 为各种其他摄动加速度矢量。r 和v r= 分别为导航探测； tr 为大行星在日心黄 r 道坐标系中的位置矢量，且 t r= t ； rr r 为大行星相对探测器的位置矢量，且 r r t = − r 并 [4]。 r r 且 r r= 忽略次要摄动力的影响建立探测器接近段状态模型为： + ω x + ω y + ω z x y z dx V = dt dy V = dt dz V = dt dV x dt dV y dt dV z dt ⎧ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ = − = − ( ( = − ( （2-2） + ω V x + ω V y + ω V z µ s r 3 µ s r 3 µ s r 3 + + + 3 AG x ) mr AG y ) mr AG z ) mr 3 3 -3-

中国科技论文在线 http://www.paper.edu.cn 选择状态矢量和状态噪声矢量为： x [ = [ = x y v v v X t ( ) ] T y x z tω ω ω ω ω ω ω ( ) ] T v x z x y v v x z 则：（2-3） + 表达航天器运动的状态方程如下所示： + 2 y 2 x → |r = | 2 z （2-4） X t ( ) = 2.1.2 系统观测方程 f X t [ ( ), ] t ω t + （2-5）探测器执行任务时，利用微型图像相机和分光仪对目标天体和背景星进行光学测量，获得了目标天体和背景星的图像信息。利用地平仪感知目标天体地平并实时测量观测量与地平之间的星光仰角以确定自身所在的位置。如下图所示[5]： → p 航天器 ( , V x y z , ) η → r i 地平矢量 s 恒星 → pr 目标天体中心O 图 1 目标天体的恒星仰角测量 Fig.1 Measurement of the target object stellar elevation 假设恒星在以目标天体为中心坐标系中的赤经和赤纬分别为α和β，则恒星的方向余弦为[6]： ∧ i = (cos ,sin ) α β α β β ,sin cos cos （2-6） → 设探测器到目标天体中心的距离矢量为 r x y z ，则二者有如下关系： , ) 为 ( , ；在以目标天体为中心的坐标系中的位置矢量 + 2 y + 2 z （2-7） x 根据图 1 恒星仰角的量测方程为： | 2 → |r = η = arccos( 为星光方向上的单位矢量， pr − 其中 i r i ⋅ r | | r p r | | | | ) arcsin( − ) （2-8）由目标天体中心垂直指向地平矢量 s 的矢量。 -4-

中国科技论文在线 http://www.paper.edu.cn 取仰角η作为观测量得系统的观测方程为： Z t ( ) = arccos( − cz ax by + x y z 2 2 + + + 2 ) arcsin( − R y 2 x + 2 + 2 z ) + V （2-9） λ 其中 R 为目标天体的半径，V λ为仰角误差。 2.2 计算机仿真 2.2.1 生成深空背景为了验证改进的 UD-EKF 在接近段自主导航系统中的应用前景，首先利用 5.0 Starry Night 1）探测器轨道初始轨道参数为：长半轴 7136 生成的深空背景并假定如下： a = km ，偏心率 e = 1.8 10 × − 5 ，升焦点赤经 Ω = 0.00 ，轨道倾角 65.00 i = ，近升角距0.05 ； 2）忽略探测器周围的次要恒星的光压摄动、伴随天体的引力摄动、大气阻力摄动及目标天体的非球星引力摄动； 3）系统噪声和观测噪声的统计特性： kE w [ 假定系统噪声和量测噪声满足： ] 0 = 6 1 × ； [ kE v = 且系统噪声与观测噪声互不 ] 0 相关，即 E vω [ T ] 0 = 6 1 × ； π 4）测量误差：夹角测量精度为 ' '2 ，测量时间间隔为 2 2.2.2 改进的 UD-EKF 的引入 s；固连坐标系中 z 方向上的误差主要是惯导初始对准误差和陀螺漂移率误差，误差形式如下所示[5]： • ε βε z = − z 2 yAε βη 1 + z （2-10）其中 Aε 陀螺随机漂移方差， zβ 为过程相关时间， 1η 为强度为 1 的白噪声。其误差为 y− 平面内的误差为惯导初始对准误差和速度误一阶马尔科夫过程因此影响相对较小；而 x 差相对较大；各个方向上的速度误差为惯导初始对准误差和加速度计误差，因此其误差最大 z x , [7]。也即探测器在特殊的接近段自主导航任务中有下式成立： ∆ < ∆ ∆ < ∆ ∆ ∆ 。因此，为了尽量减少 UD 分解过程中的误差积累，状态量的选择如下： v x v y v z y , , X t ( ) 对应的噪声向量为：初始状态取： = x z [ y v v y x v ]T z （2-11） tω ω ω ω ω ω ω v x [ = ( ) x z x y v v x ] T （2-12） = (0 | 0) X 6.06× [4.73 10 6 × 10 m 4.15 10 m s / 5.18 10 × × 6 6 m m 3.23 10 × m s 5.86 10 / 6 6 × 6 （2-13） m s / ]T 初始状态估计误差协方差矩阵： diag (0 | 0) P = [( 2) 2 ( 2) 2 ( 2) 2 (0.1) 2 (0.1) 2 (0.1) ] 2 （2-14）在上述假设背景条件下将以上重新编排了的状态量结合初始条件按照式 1-1 至式 1-10 的 UD-EKF 滤波进行迭代，通过 MATLAB 仿真与传统的 EKF 滤波进行比较，仿真结果如图 2-3 所示，表 1-2 为两种算法的复杂度比较。 -5-

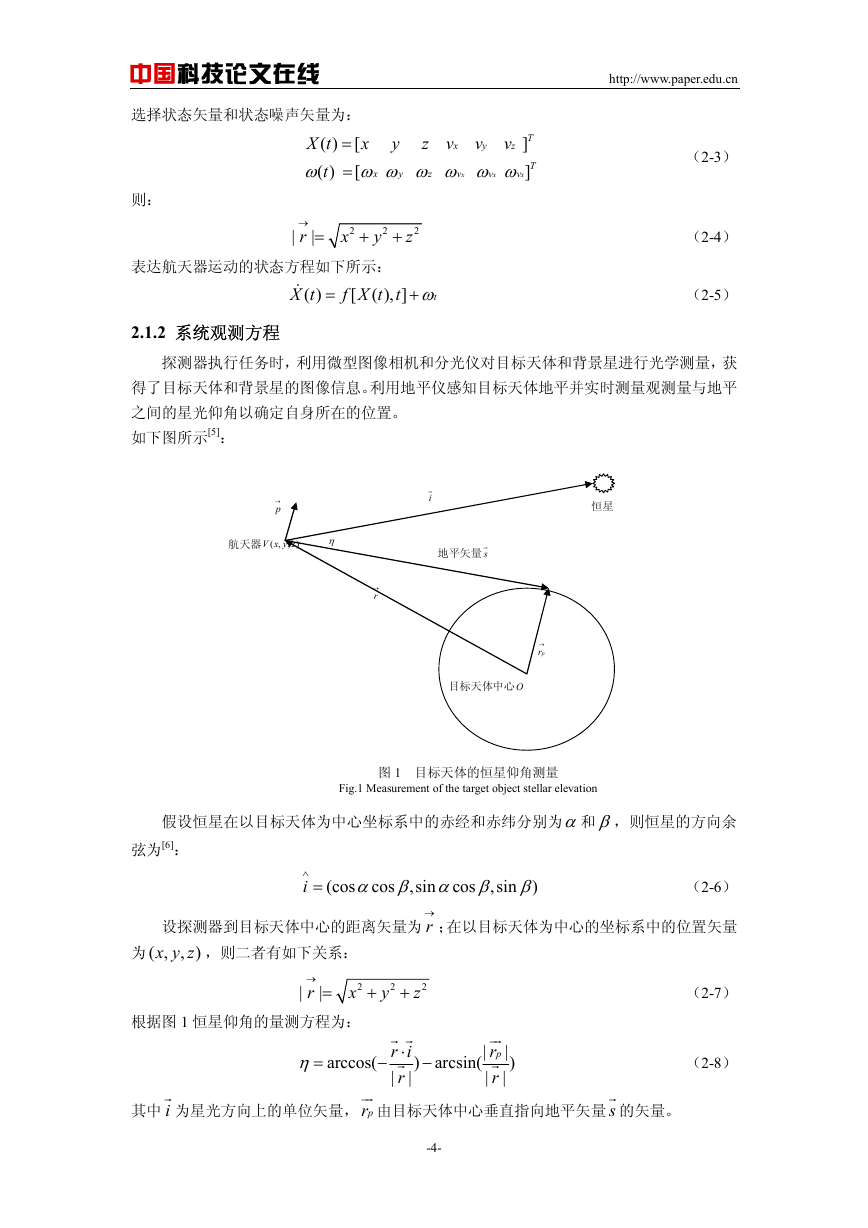
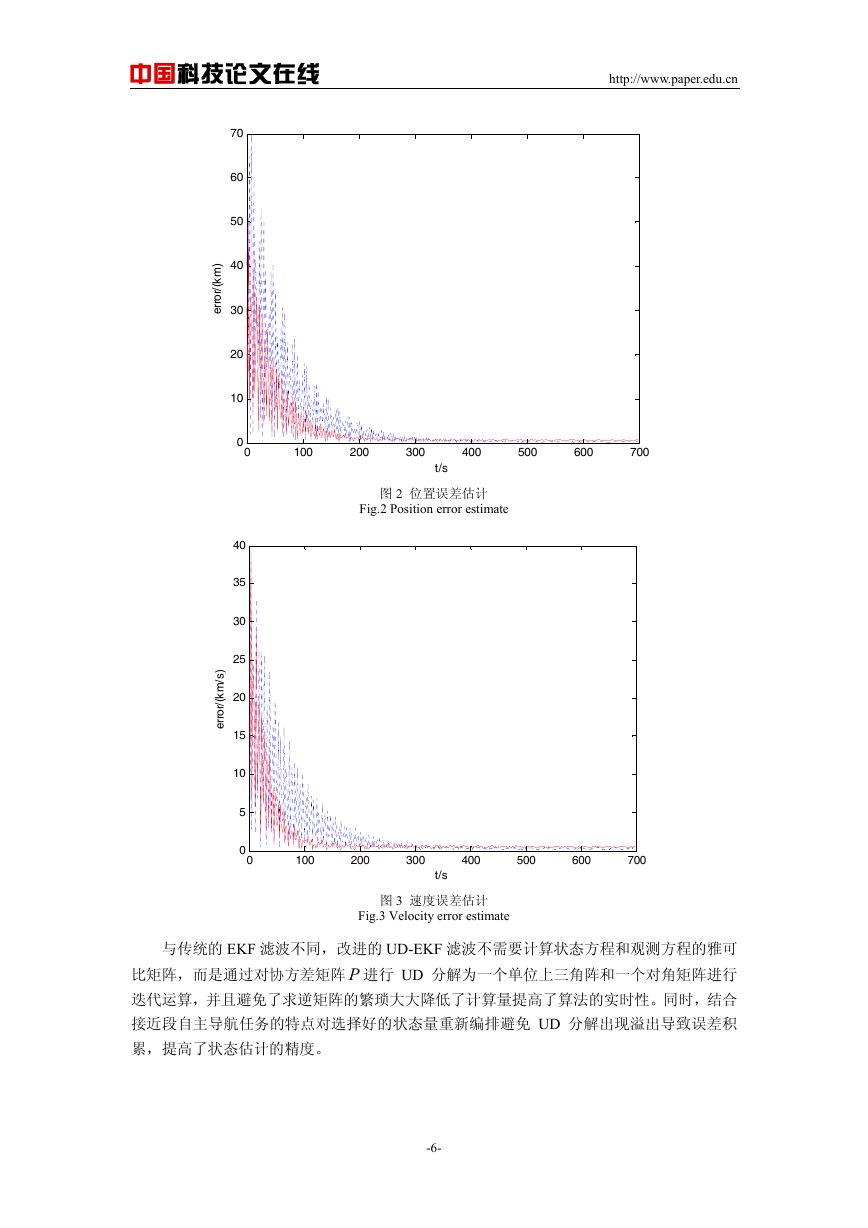
中国科技论文在线 http://www.paper.edu.cn ) m k ( / r o r r e ) s / m k ( / r o r r e 70 60 50 40 30 20 10 0 0 40 35 30 25 20 15 10 5 0 0 100 200 300 400 500 600 700 t/s 图 2 位置误差估计 Fig.2 Position error estimate 100 200 300 400 500 600 700 t/s 图 3 速度误差估计 Fig.3 Velocity error estimate 与传统的 EKF 滤波不同，改进的 UD-EKF 滤波不需要计算状态方程和观测方程的雅可比矩阵，而是通过对协方差矩阵 P 进行 UD 分解为一个单位上三角阵和一个对角矩阵进行迭代运算，并且避免了求逆矩阵的繁琐大大降低了计算量提高了算法的实时性。同时，结合接近段自主导航任务的特点对选择好的状态量重新编排避免 UD 分解出现溢出导致误差积累，提高了状态估计的精度。 -6-

中国科技论文在线 http://www.paper.edu.cn 表 1 时间更新算法时间复杂度比较算法维数 2 3 4 5 6 算法维数 2 3 4 5 6 EKF 44 126 272 500 828 表 2 观测更新算法时间复杂度比较 EKF 20 54 112 200 324 改进的UD-EKF 12 54 144 300 540 改进的 UD-EKF 23 40 61 86 115 通过计算两种算法的复杂度可知，改进的 UD-EKF 无论是时间更新还是观测更新都具有相对较少的运算量且随着维数的增加计算量的简化更为明显。能够大大减少探测器星载计算机状态估计的时间提高算法的实时性，大大满足接近段任务实时性强的要求。 3 结论本文将接近段绝对运动的动力学模型加以简化，结合目标天体的星光仰角测量模型确立了状态方程和观测方程，并将改进的 UD-EKF 滤波算法应用到接近段自主导航系统中去提高了状态估计的精度，仿真证明在接近段自主导航系统中改进的 UD-EKF 滤波与传统的 EKF 滤波相比实时性具有较大提高，能够更好的满足接近段的迅速捕获目标天体运行状态任务的要求，具有广泛的应用前景。 -7-

中国科技论文在线 http://www.paper.edu.cn 参考文献 [1]袁健. 深空探测器自主光学导航方案及非线性滤波算法研究[D].青岛：青岛科技大学, 2007. [2]冯鹏,邹世开.卡尔曼滤波器 UD 分解滤波算法的改进[J].遥感遥控,2005,26(1)：10-14. [3] 龚享铱,周良柱.一种变换空间的稳定卡尔曼滤波算法[J],长沙：电子与信息学报，2005：27（6）：896-899. [4]刘宇飞. 深空自主导航方法研究及在接近小天体中的应用[D].哈尔滨：哈尔滨工业大学, 2007. [5]胡小平.自主导航理论与应用[M].长沙：国防科技大学出版社,2002. [6] 刘伟,杨博.利用 UKF 的航天器自主导航方法研究[J].航天控制,2005,23(3)：55-59. [7]陈哲.捷联惯导系统原理[M].北京：宇航出版社,1984. [8]张树侠,孙静.捷联式惯性导航系统[M].北京：国防工业出版社,1992. Application of improved UD-EKF Filter in The Probes Approach Stage Autonomous Navigation Institute of Autonomous Navigation and Intelligent Control,Qingdao University of Science &Technology, Qingdao, Shandong (266042) Zhai Wei Abstract The state equation was established by the approach stage dynamic model. Combined with the elevation angle of star model, an improved UD-EKF filtering algorithm was put forward into the navigation scheme. The time of calculating was reduced by covariance decomposing and observations updating, and complex matrix operations were avoided too. The feasibility was proved by the computer simulation. Keywords: autonomous navigation; UD decomposing; EKF filter; elevation angle of star 作者简介：翟伟（1983—），男，青岛科技大学硕士，自主导航与智能控制研究所助理， E-mail：zhaiweiyoujian@163.com. -8-

资料库

探测器接近段自主导航的改进UD-EKF滤波算法应用.pdf

相关推荐

开发技术

热门标签

最新资料