朴素贝叶斯分类器（wine红酒数据集）.pdf-资料库

c64546cc-6ac4-45a1-8efc-b39e00bbf3a4.pdf-第1页.png

第1页 / 共7页

c64546cc-6ac4-45a1-8efc-b39e00bbf3a4.pdf-第2页.png

第2页 / 共7页

c64546cc-6ac4-45a1-8efc-b39e00bbf3a4.pdf-第3页.png

第3页 / 共7页

c64546cc-6ac4-45a1-8efc-b39e00bbf3a4.pdf-第4页.png

第4页 / 共7页

c64546cc-6ac4-45a1-8efc-b39e00bbf3a4.pdf-第5页.png

第5页 / 共7页

c64546cc-6ac4-45a1-8efc-b39e00bbf3a4.pdf-第6页.png

第6页 / 共7页

c64546cc-6ac4-45a1-8efc-b39e00bbf3a4.pdf-第7页.png

第7页 / 共7页

朴素贝叶斯分类器 2019 年 4 月 28 日目录 1 作业说明 2 解题思路 2.1 数据预处理 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2.2 理论准备 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2.3 训练集和验证集划分 . . . . . . . . . . . . . . . . . . . . . . . 2.4 求取分类准确率 . . . . . . . . . . . . . . . . . . . . . . . . . . 2.5 ROC 曲线绘制 . . . . . . . . . . . . . . . . . . . . . . . . . . 2 2 2 2 4 5 6 1

1 作业说明给定 wine 数据集，包含 178 个样本，分为三个类别，第一类 59 个样本，第二类 71 个样本，第三类 48 个样本，每个样本包含 13 个属性（酒的成分）和样本类别的标识（数字表示）。要求分别使用朴素贝叶斯方法学习样本，构建模型，并最终实现对新样本类别进行识别。已知样本数据 Xn = (x1 别 y = cn; n = f1; 2; 3g 我们的模型为： n; x2 n; : : : ; x13 n), n = 1; : : : ; 178 和样本所输类 y = f (Xn) (1) 我们的目标就是找到合适的 y, 让模型不仅和已知训练集样本适配，完整的体现训练集样本的特征，还能在实践中很好地预测测试集样本特征，也就是所谓的分类问题（监督学习）。已知样本的各维特征均属于连续型数据，所以在实际中我们可以用正态分布类型对单维度数据进行模拟。 2 解题思路 2.1 数据预处理通过观察得知，所有数据量纲虽有不一致的情况，但是使用正态分布进行模拟的时候会屏蔽掉量纲的问题，所以此处就不进行数据归一化处理。 2.2 理论准备贝叶斯分类方法是统计学中的一种经典分类方法，其分类原理就是利用贝叶斯公式根据某对象的先验概率计算出其后验概率，然后选择具有最大后验概率的类作为该对象所属的类别。之所以称之为“朴素”，是因为贝叶斯分类只做最原始、最简单的假设（所有特征之间是统计独立的）。首先，先看贝叶斯定理，P (AjB) 称之为后验，P (BjA) 称之为先验，可以从已知类别中提取，是人们对这一类别所掌握的知识，P (A) 称之为似然值,P (B) 称之为证据：

P (AjB) = P (BjA)P (A) P (B) 在本题中，可以具体化为： P (Y = ckjX = x) = ∑ P (X = xjY = ck) P (Y = ck) k P (X = xjY = ck) P (Y = ck) (2) (3) 因为朴素贝叶斯法对条件概率分布做了条件独立性假设，所以我们的似然值可以做进一步的转化： P (X = xjY = ck) = P (X1 = x1; ; X13 = x13jY = ck) = 13∏ j=1 P (Xj = xjjY = ck) (4) 将公式4代入公式3可得出： P (Y = ckjX = x) = ∑ P (Y = ck) k P (Y = ck) ∏ ∏ j P (Xj = xjjY = ck) j P (Xj = xjjY = ck) ; k = 1; 2; 3 (5) 于是我们的目标就变为在所有的类别中最大化函数值： y = f (x) = arg max ck P (Y = ck) k P (Y = ck) ∑ ∏ ∏ j P (Xj = xjjY = ck) j P (Xj = xjjY = ck) (6) 因为在三个类别中，同一样本计算过程中上述公式6的分母相同，所以在比较过程之中不需要进行该项的计算，最终我们只需要最大化如下计算式即可： y = arg max ck P (Y = ck) ∏ j P (Xj = xjjY = ck) (7) 另一个问题就是如何计算类别下某属性的条件概率值呢？当特征属性是离散值时，可以很方便地在特征样本中进行直接统计数值，最终得出结果。不过需要注意的是当某特征出现次数为 0 是应该如何处理，我们比较典型的方法就是取次数为 1，以防使最终的概率值为 0，这种校正方法在实际中经常用到。

当特征属性是非离散值时，我们最好的方法就是使用现有模型去拟合数据，并使用样本值在拟合模型之中求取条件概率数值，最常见的方法就是假定其数值服从高斯分布，似然概率值计算方法如下（代表样本标准差代表样本均值）： 1p 2 (x)2 22 e g(x; ; ) = P (xkjci) = g (xk; ci; ci) (8) (9) 2.3 训练集和验证集划分分层随机抽样，每类样本中随机划分三分之一的样本为测试集，其他为训练集。划分代码如下： for i in set(train_result_lists): # 遍历三种类别 count_of_one = train_result_lists.count(i) # 某种类型对应的频 # 随机数，采取前十个样本作为测试机样本 shuffled_num = list(range(0, count_of_one)) 合的划分顺序数 # 确定交叉验证集 random.shuffle(shuffled_num) shuffled_num = shuffled_num[0:int((1/3)*count_of_one)] shuffled_num.sort(reverse=True) # 直接获取测试集样本 # print([train_matrix_lists.pop(temp_count + num) for num in # 逆序排列 shuffled_num]) test_matrix_lists.extend([train_matrix_lists.pop(temp_count + num) for num in shuffled_num]) test_result_lists.extend([train_result_lists.pop(temp_count + num) for num in shuffled_num]) # print([shuffled_num[num] + temp_count for num in range(0, 10 temp_count += count_of_one - int((1/3)*count_of_one) )])

2.4 求取分类准确率准确率的求取方式，我使用的是十次循环迭代，求取平均值，为保证随机性，每一次训练集和测试集的划分都保证其随机性，并在最终的过程之中得到体现，另外为了防止迭代下溢，我使用自然对数函数将乘法转化为了加法进行相似度比较，以下展示用样本到类型样本集合中计算相似的所使用的函数： def get_mean(attributes): # 获取均值向量 return np.mean(attributes , axis=0) def get_std(attributes): # 获取方差向量 average = get_mean(attributes) variance = np.sum((attributes - average)**2, axis=0)/float(len (attributes)) return np.sqrt(variance) def get_prior(x_list): prior_list = [] for num in set(x_list): prior_list.append(list(x_list).count(num)/len(x_list)) return prior_list def get_Likelihood(x, mean , std): # 获取似然概率密度 exponent = np.exp(-(x-mean)**2/(2*std**2)) return (1/(np.sqrt(2*math.pi)*std))*exponent def get_jointLikelihood(x_list , mean_list , std_list): # 运用拉 likelihood = 0 for x in range(0, len(x_list)): 普拉斯方法 likelihood += math.log(get_Likelihood(x_list[x], mean_list[x ], std_list[x])) return likelihood def get_hypothesis(prior_list , x_list , mean_lists , std_lists): grade_list = [] for k in range(0, 3):

grade_list.append(math.log(prior_list[k]) + get_jointLikelihood(x_list , mean_lists[k], std_lists[k])) return grade_list.index(max(grade_list))+1 分类准确率为：0.9810344827586207 然后使用最后一次迭代的参数计算混淆矩阵等相关数值：类型类型一类型 2 类型三类型一 18 类型二 0 类型三 0 1 22 0 0 1 16 表 1: 混淆矩阵运算数值：类型正确率类型一 1.0 类型二 0.9565217391304348 类型三 0.9411764705882353 召回率 0.9473684210526315 0.9565217391304348 1.0 F 值（调和平均值） 0.972972972972973 0.9565217391304348 0.9696969696969697 表 2: 计算数值 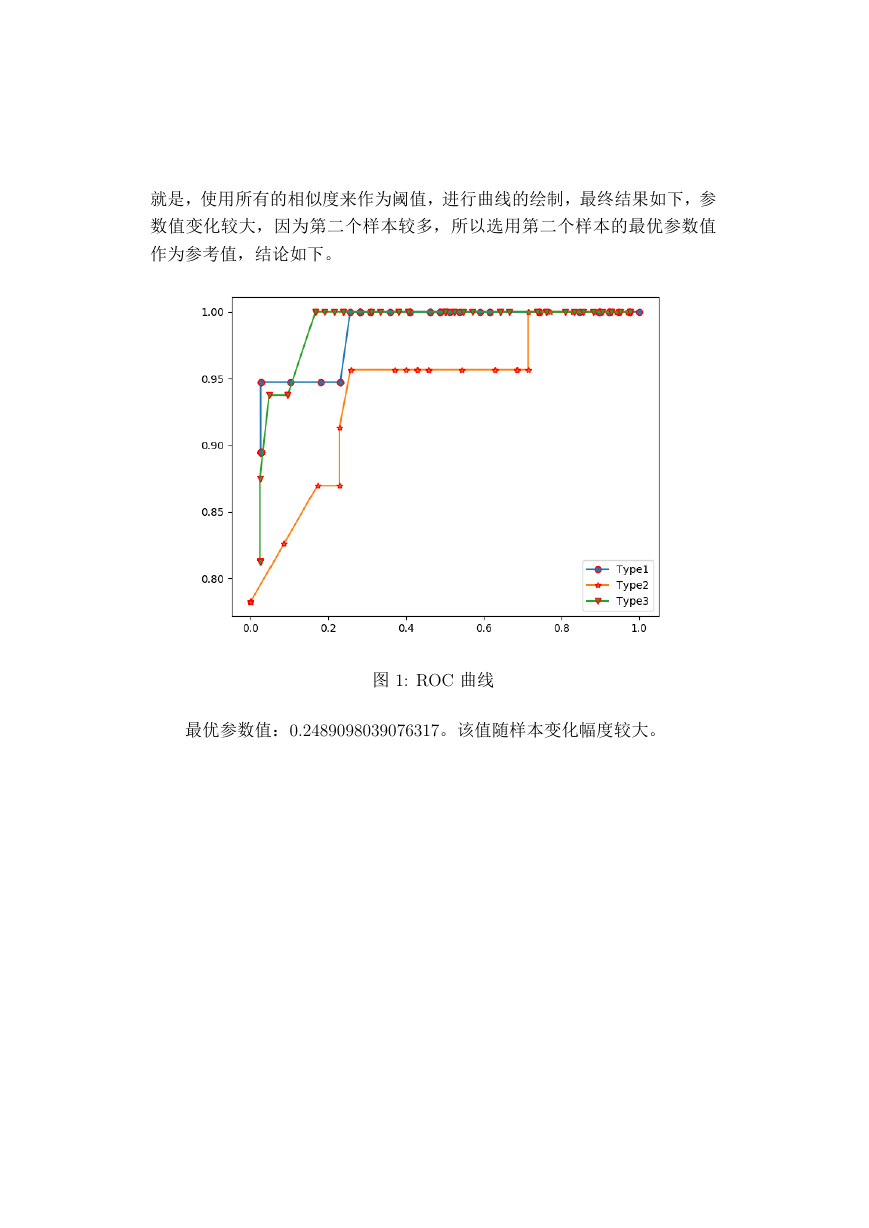2.5 ROC 曲线绘制 ROC 曲线指受试者工作特征曲线 / 接收器操作特性曲线, 是反映敏感性和特异性连续变量的综合指标, 是用构图法揭示敏感性和特异性的相互关系，它通过将连续变量设定出多个不同的临界值，从而计算出一系列敏感性和特异性，再以敏感性为纵坐标、（1-特异性）为横坐标绘制成曲线，曲线下面积越大，诊断准确性越高。在 ROC 曲线上，最靠近坐标图左上方的点为敏感性和特异性均较高的临界值。本题目中比较难选择的是阈值，因为相似度在度量过程之中量级相差超过 50，进行非线性变换后，依然相差较大，所以我在此题中绘制的思路

就是，使用所有的相似度来作为阈值，进行曲线的绘制，最终结果如下，参数值变化较大，因为第二个样本较多，所以选用第二个样本的最优参数值作为参考值，结论如下。图 1: ROC 曲线最优参数值：0.2489098039076317。该值随样本变化幅度较大。

资料库

朴素贝叶斯分类器（wine红酒数据集）.pdf

相关推荐

人工智能

热门标签

最新资料