双层网络上的演化博弈.pdf

发布时间：2022-05-29 发布人：admin 分类：说明书资料大小：0.41M 资料格式：pdf 举报版权申诉

weixin_38625351-12163768-4744302542855808716.pdf-第1页.png

第1页 / 共6页

weixin_38625351-12163768-4744302542855808716.pdf-第2页.png

第2页 / 共6页

weixin_38625351-12163768-4744302542855808716.pdf-第3页.png

第3页 / 共6页

weixin_38625351-12163768-4744302542855808716.pdf-第4页.png

第4页 / 共6页

weixin_38625351-12163768-4744302542855808716.pdf-第5页.png

第5页 / 共6页

weixin_38625351-12163768-4744302542855808716.pdf-第6页.png

第6页 / 共6页

文本预览

中国科技论文在线 http://www.paper.edu.cn 双层网络上的演化博弈陈长权，代琼琳，杨俊忠** （北京邮电大学理学院, 北京 100876）摘要：在这个工作中，研究双层网络上的演化博弈，通过引入合作为显性或者背叛为显性来关联两层网络。设定个体在一层网络进行囚徒困境博弈，在另一层网络上进行雪堆博弈。探索在不同网络层中合作者所占比例与博弈参数和网络中初始时刻合作者所占比例的依赖关系。在双层二维方格子网络中的结果为：当合作为显性时，网络中初始时刻合作者所占比例强烈影响进行囚徒困境博弈的网络层中合作者所占比例，但并不影响进行雪堆博弈的网络层中合作者所占比例。在背叛为显性时，网络中初始时刻合作者所占比例既影响进行囚徒困境博弈的网络中合作者所占比例，也影响影响进行雪堆博弈的网络上合作者所占比例。还发现在混合的显隐性模式下，进行雪堆博弈的网络层中可能存在最佳的混合概率，使得网络层上的合作者所占比例达到最大值。关键词：复杂网络；演化博弈；双层网络；显性策略中图分类号：O414.21+1 Evolutionary games in two-layer networks CHEN Changquan, DAI Qionglin, YANG Junzhong (School of Science, Beijing University of Posts and Telecommunications, Beijing 100876) Abstract: In this work, we study evolutionary games in two-layer networks by introducing the correlation between two layers through the C-dominance or the D-dominance. We assume that individuals play the Prisoner's Dilemma game (PDG) in one layer and the Snowdrift game (SDG) in the other. We explore the dependence of the fraction of the strategy cooperation in different layers on the game parameter and initial conditions. The results on two-layer square lattices show that, when cooperation is the dominant strategy, initial conditions strongly influence cooperation in the PDG layer while have no impact in the SDG layer. When defection is the dominant strategy, initial conditions influence cooperation in the PDG layer and the SDG layer. We also find that when in a mixing strategy, players in the SDG layer may exist a maximun in a appropriate probability. Key words: complex network; evolutionary game; two-layer network; dominant strategy 5 10 15 20 25 30 0 引言演化博弈理论是研究在很多领域合作行为出现和保持的一个数学模型，该理论的基础问题是在自私个体之间研究合作的演化和保持。在过去的二十年间，很多研究显示，种群的结构对合作的行为有重大影响[1-3]。比如说：在进行囚徒困境博弈的网络中合作者通过形成紧密的团簇结构来防止背叛者的入侵[1]。作为对比，进行雪堆博弈的网络中合作者的种群结构 35 更倾向于形成一种树突状[2]。具体地，Szolnoki A 研究了度混合模式对 SF 网络中合作的影响。发现了在度同配网络中，度大的点趋向于和度大的点相互连接，破坏了合作的维持，促进了背叛者的入侵；对应在度异配的网络中，中心节点之间的隔离性保护了合作的中心节点作者简介：陈长权,男,复杂网络上的演化博弈动力学通信联系人：代琼琳（1979-），女，副教授，网络博弈等. E-mail: qldai@bupt.edu.cn - 1 -

中国科技论文在线 http://www.paper.edu.cn 保持他们原始的策略避免消亡[3]。考虑了网络拓扑对合作演化的影响，为进一步研究网络中的合作演化，很多物理学家们将不确定性因素加入网络拓扑中，即考虑噪声对合作演化的影响。Szolnoki A 工作中，他们研究进行公共物品博弈不同规则网络中合作演化与策略更新过程中噪声的关系。发现了团体越大越有利于合作演化；还发现噪声较小的时候，团体中出现 5 了相变点[4]。以上的所有这些工作都是基于单层网络上的研究，在最近的几年里，多层网络上的演化博弈理论已经吸引了很多物理学家的兴趣。物理学家们研究了双层网络上的种群结构对合作演化的影响[5-12]。最近两篇综述性的文章提供了在多层网络上的一些基本概念等信息，并对多层网络上的 10 一些研究文章中出现的有趣现象做了个总结[5-6]。具体地，比如 Wang B 等人在双层进行不同的演化博弈的相互依赖的网络上研究合作演化动力学[7]。他们发现，随着网络依赖性的增加，进行囚徒困境博弈的网络层中合作水平显著提升，反之，进行雪堆博弈的网络层中合作水平有所下降。在 Wang Z 等人的工作中，他们发现当在一层网络中选择一半的个体与另一网络层中个体相连，并且个体收益受另一层网络中连接点的收益影响越大，越有利于合作的 15 演化[8]。 1 模型 1.1 初始网络结构研究了在两层相互依赖的网络上的合作演化动力学。每层网络上都有 N 个个体。设定在一层网络上进行囚徒困境博弈，在另一层网络上进行雪堆博弈。 20 研究的是方格子网络。这里设定进行囚徒困境博弈的网络为网络 A，进行雪堆博弈的网络为网络 B。网络 A 和网络 B 都是二维方格子网络，大小为，并且具有周期边界条件和冯·诺依曼邻居。两个网络上都没有空的地址，网络上的每个格点都被一个个体占据，A 网络中的个体数等于 B 网络中的个体数，并且所有的个体都被周围四个个体包围着。网络 A 中的个体从 1 编号到 10000，网络 B 中的个体也从 1 编号到 10000，并且两个网络中 25 对应点对应编号一一连接。 1.2 初始节点状态网络中的处于节点位置上的个体状态只有两种，一种为合作者，另一种为背叛者。初始时刻我们会以一定的概率给网络上的所有个体赋予合作者或者背叛者。 1.3 累积收益过程 30 为了将网络 A 与网络 B 中的个体相关联起来，这里将两网络中对应编号的个体作为一组策略对。将遗传学中的显隐性规则引入该模型中，则每组策略对可以看成是一组等位基因，这里引入两种累积收益的机制，主要有以下两种方式：（1）当合作为显性时（类似于遗传学中合作为显性时），A、B 网络中对应编号对应点，只要其中有一个为合作者时，两个个 - 2 - 100100

中国科技论文在线 http://www.paper.edu.cn 体进行累积收益的时候都表现为合作者，这种情况的策略对有（C，C）、（C，D）、（D， C）；只有当两个个体都表现为背叛者时，两个个体进行累积收益的时候才表现为背叛者，这种情况的策略对只有（D，D）。（2）当背叛为显性时（类似于遗传学中背叛为显性时）， A、B 网络中对应编号对应点，只要其中有一个为背叛者时，两个个体进行累积收益的时候都表现为背叛者，这种情况的策略对有（C，D）、（D，C）、（D，D）；只有当两个个 5 体都表现为合作者时，两个个体进行累积收益的时候才表现为合作者，这种情况的策略对只有（C，C）。两层网络中的个体只与本网络中的个体进行累积收益，只不过个体的表现形式受另一网络中对应点个体状态的影响。这里将囚徒困境博弈和雪堆博弈的收益矩阵进行重新调节，使 10 之只依赖于一个参数 r。对于囚徒困境博弈我们将收益矩阵改写为，对于雪堆博弈将收益矩阵改写为，这里参数 r 的取值范围为[0，1]。 1.4 策略更新规则这里采取的策略更新规则为费米演化规则。在网络 A 中或者网络 B 中，每个个体 x 随 15 机选取它的一个邻居 y，并且会根据两者收益的差值决定下一轮中学习 y 所采取的策略的概率。其中，学习策略的概率根据统计物理中费米函数给出：（1）这里为网络 A 或网络 B 中个体 x 的总收益，为网络 A 或网络 B 中个体 y 的总收益，需要强调的是本网络中的个体只与本网络中的个体相互作用。表示策略更新过 20 程中的选择强度。对于一个给定的值，若 x 的总收益小于 y 的总收益，则 x 倾向于学习 y 的策略，并且两者的收益差值越大，越倾向于学习 y 的策略；当然若 x 的总收益大于 y 的总收益，也有可能学习 y 的策略，只不过这时候的概率很小。如果，选择强度就很强，只要 x 的收益低于 y 的收益，x 就采取 y 的策略，若，选择强度就很弱，过程由随机漂移主导，策略更新完全是随机的。在这篇工作中，取 0.1。 25 2 计算结果如果没有特别说明，所有的数据都是经过 10000 步的演化后达到稳定状态，在选取之后的 1000 步的值取平均得到的，同时，所有的结果也都是经过了 50 次系统平均得到的结果。引入系统平均可以很好地消除网络初始时刻的不同合作者比例而引起的误差。这个工作中采用的更新方式为同步更新。 30 2.1 合作为显性合作为显性时的时间演化图如图 1 所示。图 1(a)为进行囚徒困境博弈的网络层，图 1(b) 为进行雪堆博弈的网络层。具体地，表示进行囚徒困境博弈的网络上初始时刻合作者所 - 3 - 011RrrPTS0111rr]/)exp[(11W,,BAyBAxx,BAy,BA0ac

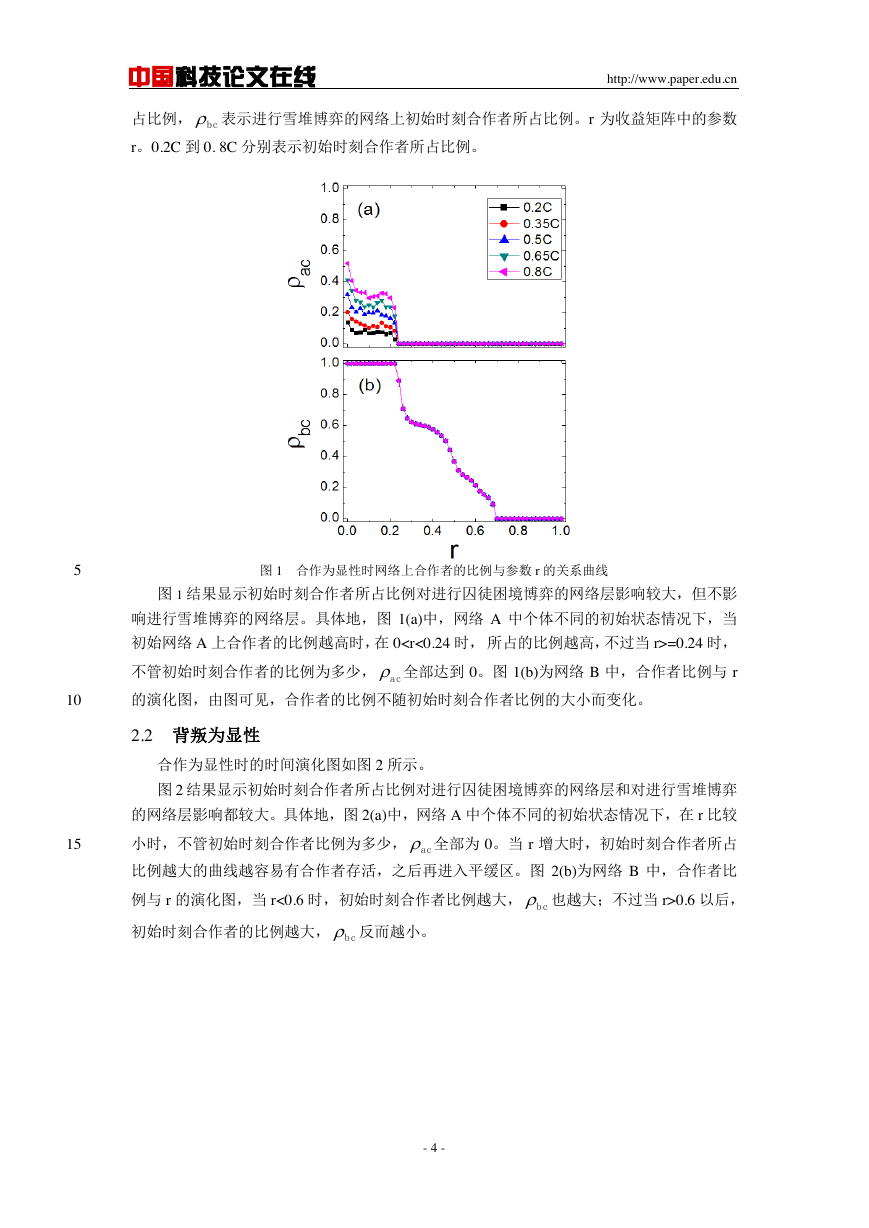
中国科技论文在线 http://www.paper.edu.cn 占比例，表示进行雪堆博弈的网络上初始时刻合作者所占比例。r 为收益矩阵中的参数 r。0.2C 到 0. 8C 分别表示初始时刻合作者所占比例。 5 图 1 合作为显性时网络上合作者的比例与参数 r 的关系曲线图 1 结果显示初始时刻合作者所占比例对进行囚徒困境博弈的网络层影响较大，但不影响进行雪堆博弈的网络层。具体地，图 1(a)中，网络 A 中个体不同的初始状态情况下，当初始网络 A 上合作者的比例越高时，在 0=0.24 时，不管初始时刻合作者的比例为多少，全部达到 0。图 1(b)为网络 B 中，合作者比例与 r 10 的演化图，由图可见，合作者的比例不随初始时刻合作者比例的大小而变化。 2.2 背叛为显性合作为显性时的时间演化图如图 2 所示。图 2 结果显示初始时刻合作者所占比例对进行囚徒困境博弈的网络层和对进行雪堆博弈的网络层影响都较大。具体地，图 2(a)中，网络 A 中个体不同的初始状态情况下，在 r 比较 15 小时，不管初始时刻合作者比例为多少，全部为 0。当 r 增大时，初始时刻合作者所占比例越大的曲线越容易有合作者存活，之后再进入平缓区。图 2(b)为网络 B 中，合作者比例与 r 的演化图，当 r<0.6 时，初始时刻合作者比例越大，也越大；不过当 r>0.6 以后，初始时刻合作者的比例越大，反而越小。 - 4 - bcacacbcbc

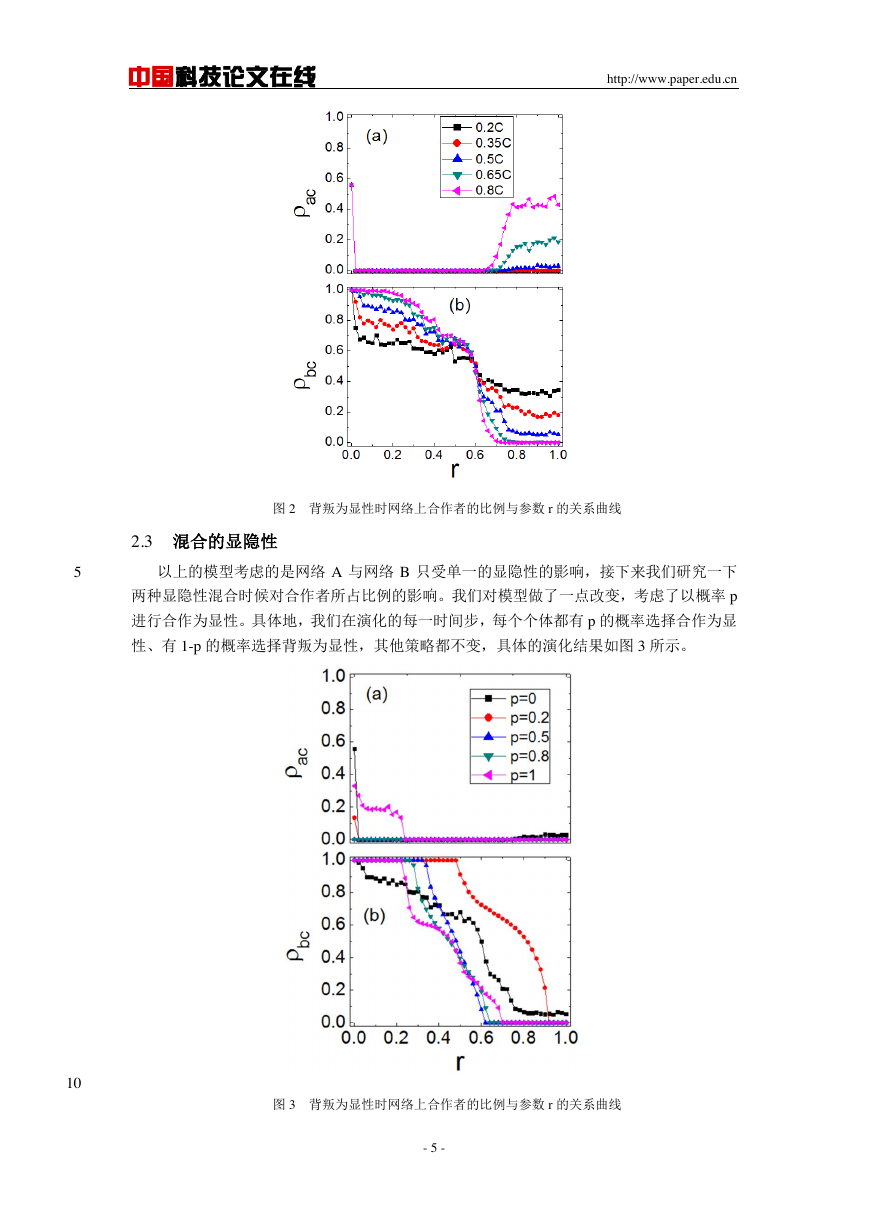
中国科技论文在线 http://www.paper.edu.cn 图 2 背叛为显性时网络上合作者的比例与参数 r 的关系曲线 2.3 混合的显隐性 5 以上的模型考虑的是网络 A 与网络 B 只受单一的显隐性的影响，接下来我们研究一下两种显隐性混合时候对合作者所占比例的影响。我们对模型做了一点改变，考虑了以概率 p 进行合作为显性。具体地，我们在演化的每一时间步，每个个体都有 p 的概率选择合作为显性、有 1-p 的概率选择背叛为显性，其他策略都不变，具体的演化结果如图 3 所示。 10 图 3 背叛为显性时网络上合作者的比例与参数 r 的关系曲线 - 5 -

中国科技论文在线 http://www.paper.edu.cn 在图 3 中，我们发现网络 A 中合作者所占比例、网络 B 中合作者所占比例与概率 p 强相关。图 3(a)中，我们发现在参数 r 值较小的时候，只有概率 p 为 1 时（即只有合作为显性的影响）合作者还存在，在混合的显隐性模式下，合作者完全消亡了。相反当参数 r 值较大时，只有概率 p 为 0 时（即只有背叛为显性的影响）合作者还存在，在混合的显隐性模式下，合作者完全消亡了。因此进行囚徒困境博弈的网络层中，混合的显隐性模式并不利于合作的演化。在图 3(b)中，当概率 p 为 0 或者概率 p 为 1 时，与我们之前得到的图形完全一致。但是在混合的显隐性模式下，我们发现当概率 p 值较小时（即背叛为显性占优），合作者所占比例相对较大；随着概率 p 的增大，合作者所占比例随着 r 的不同，占优的 p 值也不同，当 r 值小于 0.54 时，p 值越小合作者所占比例越高，当 r 值大于 0.54 时，p 值越大合作者所占比例越高。特别的是，在图 3(b)中，我们发现可能存在一个最佳的概率 p，使得进行雪堆博弈的网络层上的合作者所占比例达到最大值。 5 10 3 结论综上所述，考虑在双层网络上不同的网络层进行不同的演化博弈，比如模型中，一个网络层进行囚徒困境博弈，另一层进行雪堆博弈。通过在两层网络上引入合作为显性和背叛为 15 显性的关联性，来研究在双层网络上合作者的演化模型。发现了在合作为显性时，网络中初始时刻合作者所占比例影响进行囚徒困境博弈的网络中合作者所占比例，但不影响进行雪堆博弈的网络上合作者所占比例。在背叛为显性时，网络中初始时刻合作者所占比例既影响进行囚徒困境博弈的网络中合作者所占比例，也影响影响进行雪堆博弈的网络上合作者所占比例。还发现在混合的显隐性模式下，进行雪堆博弈的 20 网络层中可能存在最佳的混合概率，使得网络层上的合作者所占比例达到最大值。 [参考文献] (References) [1] Nowak M A, May R M. Evolutionary games and spatial chaos[J]. Nature, 1992, 359: 826-829. [2] Fu F, Nowak M A, Hauert C. Invasion and expansion of cooperators in lattice populations: prisoner's dilemma vs. snowdrift games[J]. J. Theor. Biol., 2010, 266(3): 358-366. [3] Rong Z H, Li X, Wang X F. Roles of mixing patterns in cooperation on a scale-free networked game[J]. Phys. Rev. E, 2007, 76: 027101. [4] Szklnoki A, Vukov J, Szabó G. Topology-independent impact of noise on cooperation in spatial public goods games[J]. Phys. Rev. E, 2009, 80(2): 056112. [5] Wang Z, Wang L, Szolnoki A, et al. Evolutionary games on multilayer networks: A colloquium[J]. Eur. Phys. J. B, 2015, 88(5): 1-15. [6] Kenett D Y, Perc M, Boccaletti S. Networks of networks - An introduction[J]. Chaos Solitons Fractals, 2015, 80: 1-6. [7] Wang B, Pei Z, Wang L. Evolutionary dynamics of cooperation on interdependent networks with the Prisoner's Dilemma and Snowdrift Game[J]. Europhys. Lett., 2014, 107(5): 58006. [8] Wang Z, Szolnoki A, Perc M. Optimal interdependence between networks for the evolution of cooperation[J]. Sci. Rep., 2013, 3(34): 2470. [9] Wang Z, Szolnoki A, Perc M. Self-organization towards optimally interdependent networks by means of coevolution[J]. New J. Phys., 2014, 16(3): 033041. [10] Jiang L L, Perc M. Spreading of cooperative behaviour across interdependent groups[J]. Sci. Rep., 2013, 3(8): 2483. [11] Wang Z, Szolnoki A, Perc M. Interdependent network reciprocity in evolutionary games[J]. Sci. Rep., 2013, 3(1): 1183. [12] Wang Z, Szolnoki A, Perc M. Evolution of public cooperation on interdependent networks: the impact of biased utility functions[J]. Europhys. Lett., 2012, 97(4): 48001. 25 30 35 40 45 - 6 -

分享到：

赞收藏

资料库

双层网络上的演化博弈.pdf

相关推荐

开发技术

热门标签

最新资料