logo资料库

高阶带通滤波器的设计.pdf

发布时间：2022-06-21 发布人：admin 分类：说明书 资料大小：0.33M 资料格式：pdf 举报 版权申诉
第1页 / 共7页
第2页 / 共7页
第3页 / 共7页
第4页 / 共7页
第5页 / 共7页
第6页 / 共7页
第7页 / 共7页
资料共7页，全文预览结束
    第25卷第6期 2007年12月 嘉应学院学报(自然科学) JOURNAL OF JIAYING UNIVERSITY(NATURAL SCIENCE) V01．25 No．6 Dec．20cr7 高阶带通滤波器的设计 陈昭炎 (嘉应学院物理系，广东梅州514015) [摘要]以椭圆函数滤波器为例，讨论了如何采用低通和高通椭圆函数滤波器进行高阶带通滤波器 设计方法。利用MATLAB提供的函数，设计了椭圆函数带通滤波，并用EDA对该滤波器进行了仿真。 该方法可使椭圆函数滤波器的设计变得更加简单、快捷、直观。 [关键词]椭圆有理函数；带通滤波器；MATLAB与Multisim仿真 [中图分类号]TP 274．2 [文献标识码】A [文章编号】1006-642X(2007)06-0013一06 O 引言 凡是有能力对信号频谱进行处理的装置都可以称为滤波器。在各类电子设备中，滤波器应用极 为广泛，滤波器的优劣直接决定产品的优劣。由于计算机技术、集成工艺和材料工业的发展，滤波器 的发展上了一个新台阶，并且朝着低功耗、高精度、小体积、数字化方向努力。现以2 400 Hz一3 400 Hz带通滤波器为例，介绍如何采用低通和高通椭圆函数滤波器进行设计，借助MATLAB和EDA技 术对滤波器进行设计与仿真，并根据仿真结果对参数进行修改，使滤波器的性能满足设计的要求。 1 滤波器传递函数的表示形式 N阶滤波器的传递函数的一般形式为 郴，=器=等等等若等 ㈩ 式中，m≤凡；6。，b。一l’．…”，bo和口。一1，．“，a。是滤波器网络有关参数。 根据线性网络理论…，一个复杂的传递函数可以分解成几个简单传递函数的乘积，若，t为偶数 时，分解成n／2个二阶滤波器的级联；若，l为奇数时，分解成一个一阶滤波器和(，l一1)／2个二阶滤 波器的级联。因此，二阶滤波器是组成高阶滤波器的基本单元。根据(1)式并令ao=∞2，口。=o．030可 得二阶滤波器的传递函数为： A(。)：掣!生甚 广+aO)o$+∞； (2) 式中，∞。为滤波器的固有频率，a表示滤波器的阻尼度。 2带通滤波器的设计方法 2．1滤波器的设计方案 [收稿日期]2007—09—30 [作者简介]陈昭炎(1964一)，男，广东梅州人，副教授，硕士，主要研究方向：电声、测控技术。 一13— 万方数据
    2 400 Hz一3 400 Hz带通滤波器由一个截频3 400Hz的低通滤波器和一个截频2 400 Hz的高通 滤波器级联而成。在最常用的巴特沃斯、切比雪夫、反切比雪夫和椭圆函数四种型式滤波器中，在给 定阶数和通带、阻带衰减要求的前提下，椭圆函数滤波器是最好的，具有最窄的过渡带心】。在VCVS、 三电容和双二次型三种椭圆函数滤波器电路中，双二次型椭圆函数滤波器具有带内起伏小，电路容 易调整的优点，因而在这里选用双二次型椭圆函数滤波器进行设计。根据技术要求，利用参考文 献[33中附录Ⅳ的性能表，在通带波动宽度PRW=0．1 dB，过渡带宽TⅣ=0．1 KHz条件下，当阶数Ⅳ =4时阻带最小衰减MSL=40 dB，当阶数N=5时阻带最小衰减MSL=55 dB，考虑到电阻和电容 精度带来的误差，为满足技术要求需要留有足够的余量，因而在这里选Ⅳ=5。 2．1．1设计指标 带通滤波器技术指标要求：频带宽度在2 400 Hz一3 400 Hz；带内起伏一0．1 dB；带外衰减，2 kHz 和4 kHz处衰减一55 dB。 2．1．2函数逼近问题 椭圆函数滤波器的设计基于椭圆有理函数，椭圆有理函数定义为两个多项式之比，它可由雅可 比椭圆函数导出。 样本椭圆逼近K是实变量菇的n阶有理函数：匠(菇)=8I尺(n，f，菇)I，其中尺是椭圆有理函数， 满足条件： 0≤l尺(n，亭，菇)I，l石I≤1 L(n，亭)≤lR(n，f，菇)I，f≤l菇I≤+∞ 式中￡是鉴别系数，表示当…≥f时R的最小幅值可由下式计算： ￡(n，f)=lR(n，手，孝)I。 归一化的过渡带1<龙
    图如图1所示。 其中的元件值与参数A、B、c有如下关系：p=一石e7；倒。=瓦瓦而R4 图1双二次型椭圆函数低通滤波器电路图 ；触。=之苟； 归。=巧砭1百虿。规定R：见=R1R7．,R7=Rs,用式(5)中的各项参数代入上式，解得各电阻为： 耻面A丽混=南汽=瓦1石池=A丽R7； 耻面1汽=警。 选K=l，c，=c2=o．01妒，R，=i壬=4．7 KQ，求得电阻值如表2所示。 表2椭圆函数低通滤波器电阻理论值预算 l【n 奇数阶椭圆函数低通滤波器传递函数为： 瓦V2=丽KCw,： 电路图如图2所示。选K=1，c’l=o．01斗F，尺’l=币1 K S+∞。 (1。) 、7 =7．784 kQ。 —==- 图2奇数阶椭圆低通滤波器电路图 2．2五阶椭圆函数高通滤波器的设计 五阶椭圆函数高通滤波器由2个二阶双二次型椭圆函数高通滤波器和一个奇数阶椭圆函数高 通滤波器级联而成。 低通滤波器经过频率变换可以转换成高通滤波器，低通到高通的转换关系式为： 一15一 万方数据
    式中Q=耽／耽扭为品质因数，S。=8／耽，Wo为中心频率，％定义为 5^ p；害晕；业 p2了———_2一 甄=厄瑶半…·墨>l LW3dB J5 (11) 、■1／ 可以看出，低通到高通的转换总是得到成对的^『P滤波器。 截止频率山。的二阶高通滤波器传递函数，可以在归一化低通滤波器的传递函数中以f．O。／S代替 s／E而获得。传递函数为： VK2一_妒+K(鼬(S2／+cw)：s／A+)丽 K一妒+(鼬／c)s+∞：／c (12) ¨叫 其中p=K，a=1／,4，卢=B／C，y=1／C o 因此．进行代换后，可以用图1所示电路来实现二阶高通滤波节。求得各电阻值如表3所示。 表3椭圆函数高通滤波器电阻理论值kQ 奇数阶椭圆函数高通滤波器传递函数为： 鲁=南，选矧，c，：-o．∞7一肚矗地。Q 3 3．1 matlab仿真 Matlab滤波仿真程序 椭圆函数滤波器可以实现在通带和阻带内都是等波纹的，且椭圆函数滤波器有着最窄的过渡 带，是∞的多项式，而醒(∞)是gO的有理式，椭圆函数滤波器的转移函数不但有极点，而且在如轴 上还有零点。MATLAB的信号处理工具箱提供了有关椭圆函数滤波器的函数有ellipap，eflip，ellipord [b，a]= 等，该函数的调用格式如下‘41“z，P，k]=ellipap(N，Rp，Rs) [b，a]=ellip(N，Rp，Rs) eflip(N，Rp，wn，’竹pe’，’s’)。Maflab仿真程序如下： ％设定阶数 ％通带波纹抖动(最大衰减) ％通频带下限频率 ％通频带上限频率 ％阻带最小衰减 ％求传递函数零极点和增益系数 ％求传递函数的b，a系数 ％求带通滤波的中心频率 ％求带通滤波的频带宽度 ％低通滤波变换带通滤波 ％带通滤波器的频率响应 ％画出频响的波形图 ％设定波形的显示范围 N=5： Rp=O．1； wl=2400； wh=3400； Rs=55； [z，p，k]=ellipap(N，Rp，Rs)； [b，a]=zp2ff(z，P，k)； Wo=sqrt(wl木wh)； Bw=wh—wl； [bt，at]=lp2bp(b，a，Wo，Bw)； [H，W]=freqs(bt，at)； semilogy(W，abs(H))； axis([0，6000，le一6，1．1])； Mabel(’Frequency(pi rad／s)’)； ylabel(7IH(jw)I’)； 一1 6— 万方数据
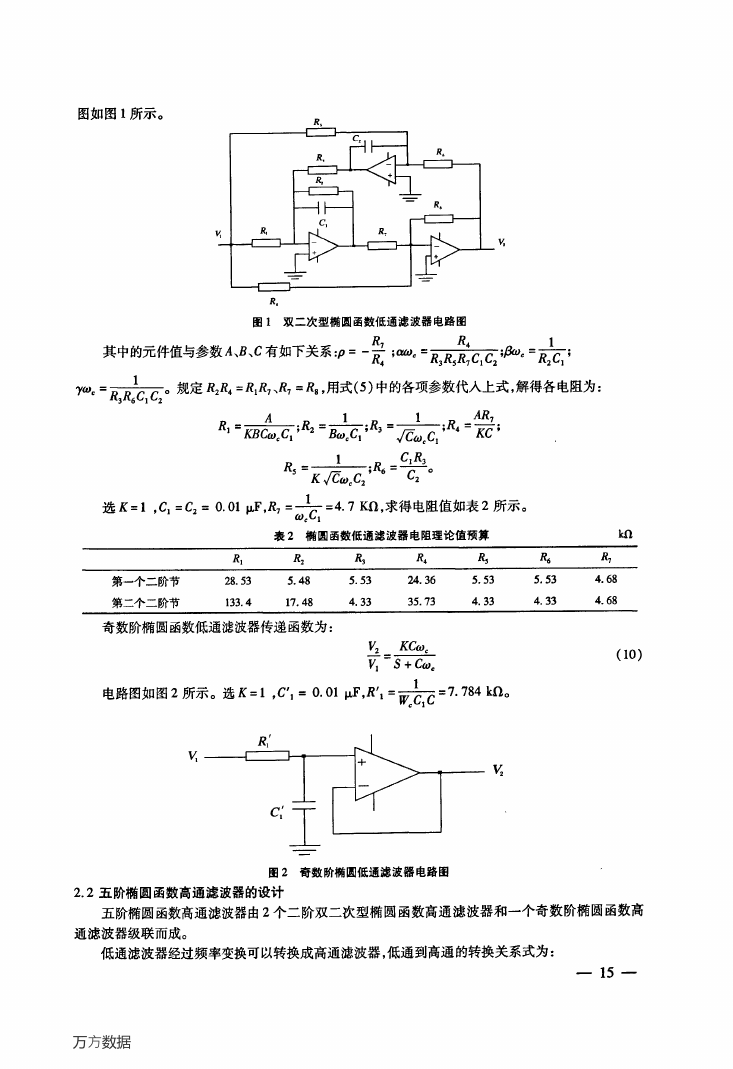
    title(‘椭圆函数带通滤波幅频响应’) 咖d on MATLAB仿真波特图如图3所示。 椭圆函数带通滤波幅频响应 善 三 Frequency(pi豫d，8) 图3眦tkIb仿真波特图 4 电路电容电阻的实际取值及仿真 根据表2、表3所得电路元件的理论值，可按元件的实际标称进行取值，即得表4。 表4椭圆函数低通滤波器电路电阻标称值 m 奇数阶椭圆函数高通滤波器电路电容电阻标称值： K=I,C'I=0．047 Is,F’彤l 2蠢。820 Q r 五阶低通椭圆滤波器和五阶高通椭圆滤波器级联后，带通的带宽为B。=厶一五=3400hZ一 2 400 hZ=1 000 hZ，带通的几何中心频率为以=“丽=V：—2 400 x—3 400=2 856．57 hZ，品质因数 一17— 万方数据
    为Q=fo／B。=2．857，用Muhisim仿真，结果如图4所示。 图4级联后带通滤波器频翠响应图 从前面的分析及其计算，我们得到了一种有源带通滤波器特征频率及放大倍率的使用计算公 式，通过适当的参数选取可以得到一定倍率、一定特征频率的具有良好的幅频特性和相频特性的有 源带通滤波器。 5 结束语 利用Matlab和Muhisim结合来设计滤波器要比传统设计步骤简便、直观的多，Matlab作为一种 交互式的程序语言，在滤波的应用中有着自己独特的优点。运用给定的信号处理工具箱函数，编制 相应的程序，可实现各种形式的模拟、数字滤波器，这对于信号的传输与处理有着极其重要的作用。 而且从Matlab和Multisim仿真可知，采用椭圆函数设计滤波器有其最窄的过渡带，由椭圆函数滤波 器也可以设计切比雪夫一型和二型滤波器，这可由实际容差要求确定采用何种函数逼近。 [参考文献】 [1]郑南雁，楚方求，程友发．有源滤波器的设计[J]．测控技术，1999。18(7)：60．． [2]MiroslavD．Lutovac．信号处理滤波器设计一基于Matlab和Mathematica的设计方法[M]．朱义胜，董辉，译．北京：电子工业出版 社，1994：109，387，456． [3]约翰逊DE，约翰逊JR，穆尔HP．有源滤波器精确设计手册[M]．李国荣，译．北京：电子工业出版社，1984：13，33，45． [4]飞思科技产品研发中心．Matlab7辅助信号处理技术与应用[M]．北京：电子工业出版社，1995：157，189． [5]张莜华，林莘．滤波技术[M]．北京：人民邮电出版社。1994：87。107—156． [6]哈里，Y—F，拉姆．模拟和数字滤波器设计与实现[M]．陆延丰，译．北京：人民邮电出版社，1985． [7]D．M．Rabrenovlc，M．D．Lutovac，Ellipticfilters withminimalQ一‰[J]．Electronicskt细，1994(30)：206—207 Design of the High—·order Band--pass Filters (Department ofPhysics，Jiaying uni傀rsity，Meizhou 514015，China) CHEN Zhao—-yan [Abstract]This article presents an elliptic function filter to explore the method of designing high—order band—pass filter using low—pass and high—pass elliptic function filters．The MATLAB built—in function is used to design the band—pass filter，and EDA is used to do did a simulation．With this method the ellip- tic function filter design will be easier，faster and more visualized． [Key words]elliptic rational function；band—pass filter；MATLAB and Multisim simulation —18一 万方数据
    高阶带通滤波器的设计 作者： 陈昭炎， CHEN Zhao-yan 作者单位： 刊名： 嘉应学院,物理系,广东,梅州,514015 嘉应学院学报 英文刊名： JOURNAL OF JIAYING UNIVERSITY(NATURAL SCIENCE) 2007,25(6) 年，卷(期)： 参考文献(7条) 1.D.M.Rabrenovie;M.D.Lutovae EUiptie filters with minimal Q-factors 1994(30) 2.哈里,Y-F;拉姆;陆延丰 模拟和数字滤波器设计与实现 1985 3.张莜华;林莘 滤波技术 1994 4.飞思科技产品研发中心 Matlab7辅助信号处理技术与应用 1995 5.约翰逊DE;约翰逊JR;穆尔HP;李国荣 有源滤波器精确设计手册 1984 6.Miroslav D.Lutovac;朱义胜;董辉 信号处理滤波器设计-基于Matlab和Mathematica的设计方法 1994 7.郑南雁;楚方求;程友发 有源滤波器的设计[期刊论文]-测控技术 1999(07) 本文读者也读过(4条) 1. 史燕.杨小雪 基于Matlab和Multisim的综合性实验——椭圆滤波器设计与仿真[期刊论文]-北华航天工业学院学 报2008,18(z1) 2. 李小英.陈子龙 低噪声带通滤波器精确设计与MATLAB仿真[期刊论文]-声学与电子工程2003(4) 3. 曾喆昭.李仁发 高阶带通滤波器设计研究[期刊论文]-通信学报2001,22(10) 4. 许碧荣.赖玉平.温丽梅.吴祯芸.XU Birong.LAI Yuping.WEN Limei.WU Zhenyun 采用Multisim软件仿真设计有 源滤波器[期刊论文]-南平师专学报2006,25(4) 本文链接：http://d.g.wanfangdata.com.cn/Periodical_jydxxb200706003.aspx
    分享到：
    赞 收藏

    相关推荐

    资料库

    移动开发

    共收录1376份资料，累计14个分类，关注成员有19位，主要包括：IOS,Symbian,webOS,WindowsPhone,小程序,Flash,BlackBerry,bada,JavaME,HTML5,iOS,Android,QT,其它

    热门标签

    IOS Symbian webOS WindowsPhone 小程序 Flash BlackBerry bada JavaME HTML5 iOS Android QT 其它

    最新资料