logo资料库

数字设计原理与实践 第四版 (john F.Wakerly ) 课后答案.pdf

发布时间：2022-06-09 发布人：admin 分类：说明书 资料大小：0.43M 资料格式：pdf 举报 版权申诉
第1页 / 共60页
第2页 / 共60页
第3页 / 共60页
第4页 / 共60页
第5页 / 共60页
第6页 / 共60页
第7页 / 共60页
第8页 / 共60页
资料共60页，剩余部分请下载后查看
    第 1 章习题参考答案: 1-6 一个电路含有一个 2 输入与门（AND2），其每个输入/输出端上都 连接了一个反相器；画出该电路的逻辑图，写出其真值表；能否将该 电路简化？ 解：电路图和真值表如下： 由真值表可以看出，该电路与一个 2 输入或门（OR2）相同。 第 2 章习题参考答案: 2.2 将下面的八进制数转换成二进制数和十六进制数。 (a) 12348=1 010 011 1002=29C16 (b) 1746378=1 111 100 110 011 1112=F99F16 (c) 3655178=11 110 101 101 001 1112=1EB4F16 (d) 25353218=10 101 011 101 011 010 0012=ABAD116 (e) 7436.118=111 100 011 110.001 0012=F1E.2416 (f) 45316.74748=100 101 011 001 110.111 100 111 12=4ACE.F2C16 2.3 将下面的十六进制数转换为二进制数和八进制数。 (a) 102316=1 0000 0010 00112=100438 (b) 7E6A16=111 1110 0110 10102=771528
    (c) ABCD16=1010 1011 1100 11012=1257158 (d) C35016=1100 0011 0101 00002=1415208 (e)9E36.7A16=1001 1110 00110110.0111 10102=117066.3648 (f)DEAD.BEEF16=1101 1110 1010 1101.1011 1110 1110 11112 =157255.5756748 2.5 将下面的数转换成十进制数。 (a) 11010112=107 (b) 1740038=63491 (c) 101101112=183 (d) 67.248=55.3125 (e)10100.11012=20.8125 (f)F3A516= 62373 (g) 120103=138 (h) AB3D16=43837 (i) 71568=3694 (j) 15C.3816=348.21875 2.6 完成下面的数制转换。 (a) 125= 1 111 1012 (b) 3489= 66418 (c) 209= 11 010 0012 (d) 9714= 227628 (e) 132= 10 000 1002 (f) 23851= 5D2B16 (g) 727= 104025 (h) 57190=DF6616 (i) 1435=26338 (j) 65113=FE5916 2.7 将下面的二进制数相加，指出所有的进位： (a) S：1001101 C：100100 (b) S: 1010001 C: 1011100 (c) S: 101000000 C: 111111110 (d) S: 11011111 C: 11000000
    2.8 利用减法而不是加法重复训练题 2.7，指出所有的借位而不是进 位： (a) D：011 001 B：110000 (b) D：111 101 B：1110000 (c) D：10000110 B：00111000 (d) D：1101101 B：11110010 2.11 写出下面每个十进制数的 8 位符号－数值，二进制补码，二进 制反码表示。 (a) +25 原码: 0001 1001 反码: 0001 1001 补码: 0001 1001 (b) +120 0111 1000 0111 1000 0111 1000 (c) +82 0101 0010 0101 0010 0101 0010 (d) –42 10101010 11010101 11010110 (e) –6 1000 0110 1111 1001 1111 1010 (f) –111 1110 1111 1001 0000 1001 0001 2.12 指出下面 8 位二进制补码数相加时是否发生溢出。 (a)1101 0100+1110 1011= 1011 1111 不存在溢出 (b)1011 1111+1101 1111= 1001 1110 不存在溢出 (c)0101 1101+0011 0001= 10001110 存在溢出 (d)0110 0001+0001 1111= 1000 0000 存在溢出 2.33 对于 5 状态的控制器，有多少种不同的 3 位二进制编码方式？ 若是 7 状态或者 8 状态呢？ 解：3 位二进制编码有 8 种形式。 对于 5 状态，这是一个 8 中取 5 的排列：N=8x7x6x5x4= 6720
    对于 7 状态，这是一个 8 中取 7 的排列：N=8x7x6x5x4x3x2= 40320 对于 8 状态，种类数量与 7 状态时相同。 2.34 若每个编码字中至少要含有一个 0，对于表 2-12 的交通灯控制 器，有多少种不同的 3 位二进制编码方式？ 解：在此条件下，只有 7 种可用的 3 位二进制码，从中选取 6 个进行 排列，方式数量为：N=7x6x5x4x3x2=5040 2.35 列出图 2-5 的机械编码盘中可能会产生不正确位置的所有“坏” 边界。 解：001/010、011/100、101/110、111/000 2.36 作为 n 的函数，在使用 n 位二进制编码的机械编码盘中有多少 个“坏”边界？ 解：有一半的边界为坏边界：2n-1。 数字逻辑第 3 章参考解答： 3.11 对图 X3.11（a）所示的 AOI 电路图，采用 AND，OR,INV 画出对 应的逻辑图。 解： ( = Z )'DCBA +⋅ +
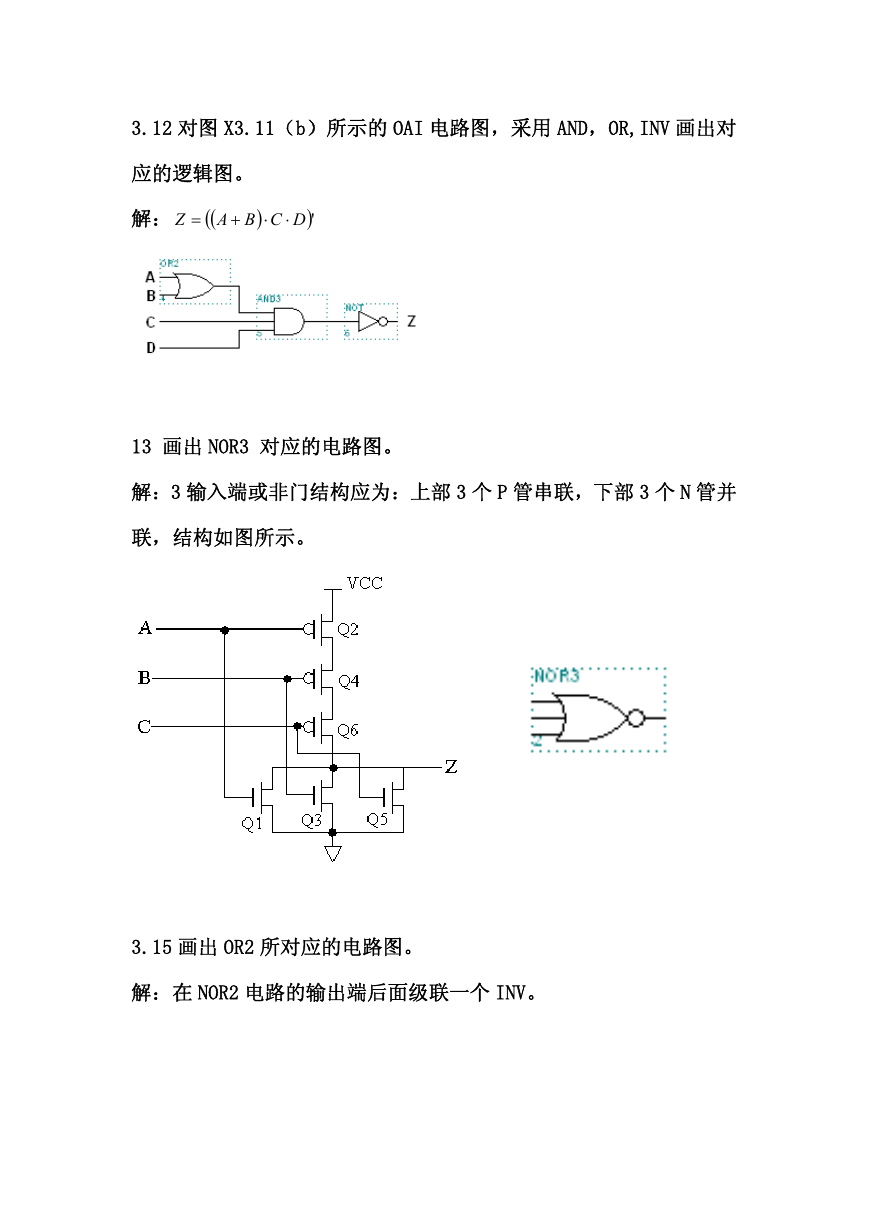
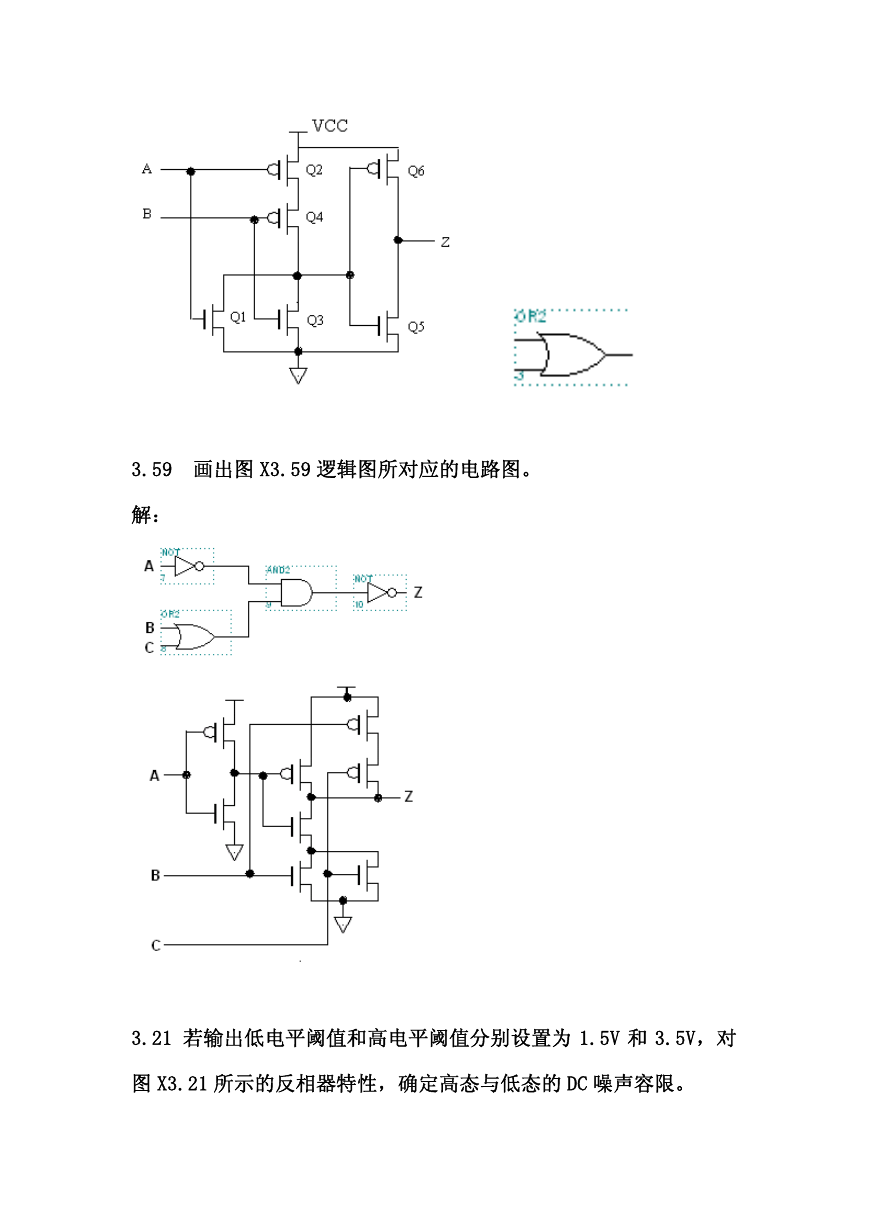
    3.12 对图 X3.11（b）所示的 OAI 电路图，采用 AND，OR,INV 画出对 应的逻辑图。 解： ( ( Z = )'DCBA + ) ⋅ ⋅ 13 画出 NOR3 对应的电路图。 解：3 输入端或非门结构应为：上部 3 个 P 管串联，下部 3 个 N 管并 联，结构如图所示。 3.15 画出 OR2 所对应的电路图。 解：在 NOR2 电路的输出端后面级联一个 INV。
    3.59 画出图 X3.59 逻辑图所对应的电路图。 解： 3.21 若输出低电平阈值和高电平阈值分别设置为 1.5V 和 3.5V，对 图 X3.21 所示的反相器特性，确定高态与低态的 DC 噪声容限。
    解：由图中可以看到，输出 3.5V 对应的输入为 2.4V,输出 1.5V 对应 的输入为 2.5V； 所以，高态噪声容限为：3.5-2.5=1 V ;低态噪声 容限为：2.4-1.5=0.9 V。 3.26 利用表 3-3 计算 74HC00 的 p 通道和 n 通道的导通电阻。 解：采用极端值计算（对商用芯片，最低电源电压设为 4.75V） 表中所列输出电压与电流关系如图所示： 根据电流定律，高态输出时可以建立下列方程： ⎛ ⎜ ⎜ ⎝ 35.0 R p − 02.0 ⎞ ⎟ =⎟ ⎠ 4.4 R n ⎛ ⎜ ⎜ ⎝ 91.0 R p − 4 ⎞ ⎟ =⎟ ⎠ 84.3 R n 联立求解可得： R p = k 151.0 =Ω 151 Ω 低态输出时可以建立下列方程： ⎛ ⎜⎜ ⎝ 02.01.0 R − n ⎞ =⎟⎟ ⎠ 65.4 R p ⎛ ⎜⎜ ⎝ 33.0 R n − 4 ⎞ =⎟⎟ ⎠ 42.4 R p 联立求解可得： Rn = .0 060 k Ω=Ω 60 3.27 对 于 表 3-3 所 列 的 74HC00 ， 若 设 VOLmax=0.33V,VOHmin=3.84V,Vcc=5V,对于下列电阻负载，确定该系列的
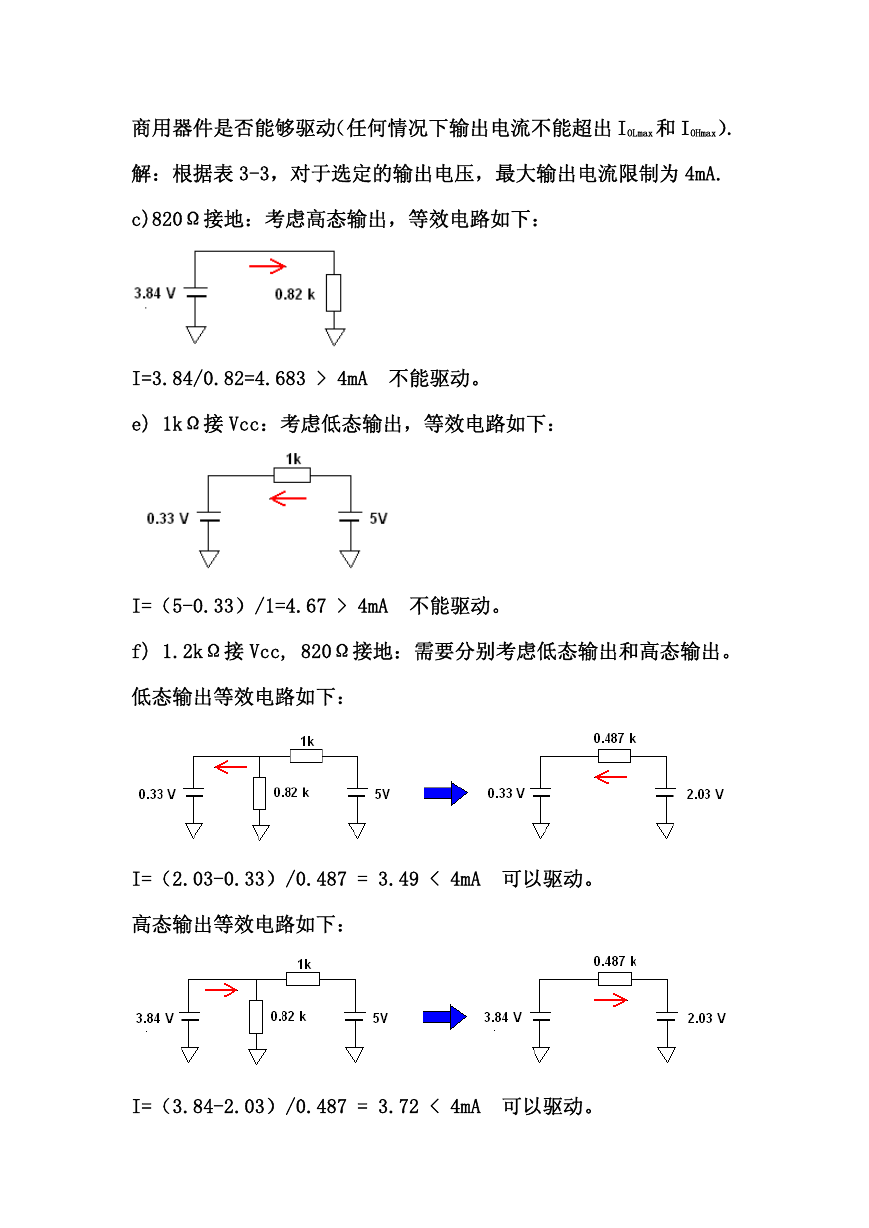
    商用器件是否能够驱动（任何情况下输出电流不能超出 IOLmax 和 IOHmax）. 解：根据表 3-3，对于选定的输出电压，最大输出电流限制为 4mA. c)820Ω接地：考虑高态输出，等效电路如下： I=3.84/0.82=4.683 > 4mA 不能驱动。 e) 1kΩ接 Vcc：考虑低态输出，等效电路如下： I=（5-0.33）/1=4.67 > 4mA 不能驱动。 f) 1.2kΩ接 Vcc, 820Ω接地：需要分别考虑低态输出和高态输出。 低态输出等效电路如下： I=（2.03-0.33）/0.487 = 3.49 < 4mA 可以驱动。 高态输出等效电路如下： I=（3.84-2.03）/0.487 = 3.72 < 4mA 可以驱动。
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料