航空航天结构有限元法

第 1 章绪论 1.1 有限元法的发展简史有限元法是一种求解微分方程的数值计算方法。与传统的解析方法相比，有限元法具有理论完善，物理意义直观明确，解题效率高等优点。随着电子计算机的发展和应用，有限元法已经成为解决许多科学和工程实际问题的有效的工具。有限元法最早的概念可以追溯到 1943 年，数学家 Courant 应用定义在三角形区域上的分片连续函数，与最小势能原理相结合，来求解 St. Venant 扭转问题。1955 年，Argyris 和 Kelsey 利用最小势能原理，得到了系统的刚度方程，推广杆系结构矩阵分析法，对连续结构进行了分析。1956 年，波音公司 Turner, Clough, Martin 和 Topp 等人在分析大型飞机结构时，第一次给出采用直接刚度法推导出的三角形单元，将结构力学中的位移法推广到平面应力问题。Clough 于 1960 年在一篇论文中首次使用“Finite Element”（有限元或有限单元）这一名称。1963 年，Besseling 等人证明了有限元法是基于变分原理的 Ritz 法的另一种形式。 1969 年，Oden 将有限元法推广应用于加权残量法（如 Galerkin 法）。同年，Zienkiewicz 提出了等参元的概念，从而使有限元法更加普及与完善。 1970 年代以后，随着电子计算机硬件和软件技术的发展，有限元法的研究和应用得到了飞速地进展。出现了一些大型结构分析软件，同时，有限元法应用的领域不断扩大。从弹性力学平面问题扩展到空间问题和板壳问题，从静力平衡问题扩展到动力响应问题和结构稳定问题，从固体力学扩展到流体力学和传热学等学科，从弹性材料扩展到弹塑性、塑性、粘弹性、粘塑性和复合材料等，从航空领域扩展到宇航、土木建筑、机械制造、水利工程、造船与核工程等领域。 1.2 弹性力学的基本概念有限元法是在求解弹性力学平面问题时显露其有效性的。这是由于弹性体的变形能和外力势可以表示为形式划一的二次泛函。为了浅显地介绍有限元法，这里我们简要地介绍弹性力学的基本概念。 1.2.1 三维问题 1.2.1.1 应力与平衡方程弹性体在外力或者温度发生变化等条件作用下，内部各部分之间将产生内力。内力的大小通常用应力来表示，单位面积上所受到的内力就称为应力。在弹性体内的一点 P 附近作一平行微元六面体，其棱边平行于各坐标轴。微元六面体中有三个面的外法线方向分别与 x 轴、y 轴和 z 轴同向，其余三个则与坐标轴反向。作用在 - 1 -

垂直于 x 轴平面上的应力分量为,, ，作用在垂直于 y 轴平面上的应力分量为 ,,，作用在垂直于 z 轴平面上的应力分量为,,，如图 1.1 所示。这 9 个应力分量构成一个张量，称为应力张量。 z o C zσ zxτ xzτ xyτ zyτ xzτ xσ yzτ xyτ yxτ P zyτ zxτ zσ yxτ yσ yzτ xσ A yσ B y x 图 1.1 微元六面体上的应力 - 2 - 由微元六面体力矩的平衡可得切应力互等定律，即从图 1.1 中可以看出，应力分量表示垂直于 x 轴的坐标面上的正应力（受拉取正，受压为负）；而应力分量,则表示垂直于 x 轴的坐标面上的切应力（使扭转角变为锐角的为正）。 ,,,; 11 12 13 面围成的四面体的平衡条件，可以得到作用于该斜面的应力的三个分量因此，应力张量是对称的，其分量只有六个是独立的。在有限元法中，通常把六个应力分量排成下列次序的列向量经过点 P 作一任意的斜面（图 1.2），其法线 N 的方向余弦为（l, m, n），利用与三坐标

C yxτ xp yzτ P zyτ yσ A xyτ zp xσ xzτ yp zxτ zσ z o N B y x 而切应力大小为的平衡方程为图 1.2 四面体微元上的应力作用于该斜面上的正应力为力主轴，而其正应力称作 P 点的主应力。可以证明，在弹性体内任意一点，一定存在三个互相正交的主应力，其中最大（小）的一个就是该点的极大（小）正应力。三个正应力之和 222 14 15 如果斜面上切应力0，则该斜面称作 P 点的应力主面，相应的法线称作 P 点的应 16 设作用于 P 点的体积力为，对微元六面体进行平衡分析，可以得到力 0 0 0 17 称为体积应力，它在坐标变换下是个不变量，因而等于三个主应力之和。 - 3 -

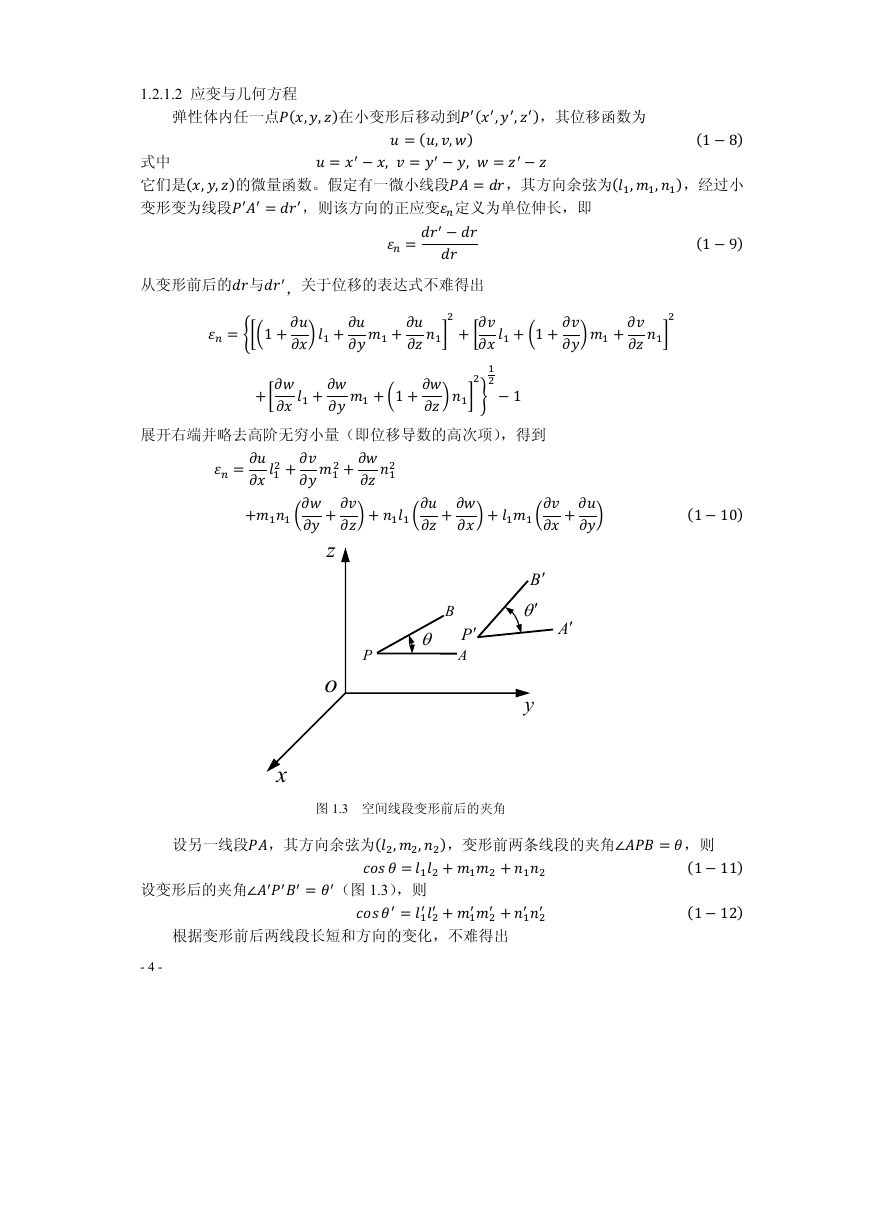
1.2.1.2 应变与几何方程弹性体内任一点,,在小变形后移动到,,，其位移函数为 ,, 18 式中 ,, 它们是,,的微量函数。假定有一微小线段，其方向余弦为,,，经过小变形变为线段，则该方向的正应变定义为单位伸长，即 19 从变形前后的与 11 11 110 展开右端并略去高阶无穷小量（即位移导数的高次项），得到，关于位移的表达式不难得出 z B P′ A θ P o B′ θ′ A′ y x 图 1.3 空间线段变形前后的夹角设另一线段，其方向余弦为,,，变形前两条线段的夹角，则 111 设变形后的夹角（图 1.3），则 112 根据变形前后两线段长短和方向的变化，不难得出 - 4 -

1 2 113 , , 114a,b,c ,, 114d,e,f 对照（1－11）和（1－13）可知，只要在 P 点给定如下六个导数值就可以完全确定 P 点邻近的变形状态。 ,,表示沿坐标轴的正应变，,, 表示经过小变形后坐标方向之间的直角改变量，即所谓切应变，如图 1.4 115 所示。变形后原直角变成锐角为正，变成钝角为负。如同切应力，切应变同样满足互等定律。这六个量称为应变分量，记作 o y x A α A′ P B P′ β B′ 图 1.4 切应变 xyγ βαγ =xy + 同样可以证明，在弹性体内任意一点，一定存在互相正交的应变主轴，变形后三轴交角仍然保持直角，即切应变为零；三主轴的应变称为主应变，而且其中最大（小）的一个就是该点的极大（小）的正应变。三个正应变之和称为体积应变，也是不变量，而且表示微元中每单位体积的改变量。对于各向同性体来说，应力主轴与应变主轴的方向是一致的。关系式（1－14）称为几何方程，其矩阵形式为 116 0 0 117 0 0 1, 21 1 118a,d 0 0 0 0 0 1.2.1.3 物理方程应变与应力之间的一般关系式，即物理方程为 - 5 -

称为剪切弹性模量。从（1－18）求逆得出应力与应变之间的关系式 1, 21 1 118b,e 1, 21 1 118c,f 式中,分别称为弹性模量和泊松比，G 21 ⁄ 2, 119a,d 2, 119b,e 2, 119c,f 2 0 0 0 或写成矩阵形式 2 0 120 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 式中 112 ⁄ 与 G 称为拉梅系数，e 是体积应变，它与体积应力成正比 12 或＝ 12 121a,b 式中比例常数 12 弹性体的边界承受面力 122 的方式有三种：固定支承，荷载支承和弹性支承。设的三种支承部分分别记为、和， ①几何约束条件：在上给定位移，即 , , 在上 123 ②面力平衡条件：在上给定荷载即面力 q，,,表示上任一面积元素的外法线方向余弦，由应力与面力平衡得到在上 124 ③耦合平衡条件：在上弹性体与另一弹性体接触，这些接触边界上的位移既不受约束也不自由，而是具有与给定位移,,成正比的弹性反力。在单位面积上它的三个分量为 1,2,3 125 这里弹性支承系数矩阵Cc是正定的，而可以看作为给定的面力。同样，这反力应由上的应力来平衡。于是，平衡条件为则边界条件可表示为 ⁄ 1.2.1.4 边界条件称为体积弹性模量。 - 6 -

在上 126 1.2.2 二维问题中面为 xy 平面，假定 z 无关，从几何方程可知对于承受拉伸的薄板，可以认为沿板厚方向的正应力和切应力都为零。通常以薄板的 1.2.2.1 平面应力问题（1）力的平衡方程题。对于受到沿长度方向不变的外力作用的相当长的棱柱体（例如水坝），可以认为各点只 0, 0 只有沿 xy 平面的三个应力分量，即,和，且与坐标 z 无关。这就是平面应力问有平行其横截面（取为 xy 平面）的位移（即0），且其位移沿长度方向不变（即 u, v 与 0, 0 有沿 xy 平面的三个应变分量，即,和，且与坐标 z 无关。这就是平面应变问题。 0 0 127 , , 128 1 1 129 21 1 1 21 130 （2）几何方程（3）物理方程用应变表达应力则为 - 7 -

从物理方程（1－18）还可推导出（4）边界条件为 1.2.2.2 平面应变问题 1 131 假定边界 Γ 的固定支承、荷载支承和弹性支承分别记作、和，则边界条件可表示 , 在上 132 在上 133 在上 134 力的平衡方程、几何方程和边界条件同平面应力问题一样，从0和（1－18）可推 1 1 1 1 135 21 1 121 1 用应变表达应力则为 121 1 21 对照平面应力问题的物理方程可以看出，只要把其中的,分别换为E1 1 ⁄ 136 ，就可得到平面应变问题的物理方程。 ⁄ , 出物理方程为 1.3 有限元法的基本概念 1.3.1 结构离散化有限元法的基本思想是将一个连续的求解域（连续体）离散化，即分割成彼此用结点（离散点）互相联系的有限个单元，在单元体内假设近似解的模式，用有限个结点上的未知参数表征单元的特性。然后用适当方法，将各个单元的关系式组合成包含这些未知参数 - 8 -

资料库

航空航天结构有限元法_12345.pdf

相关推荐

课程资源

热门标签

最新资料