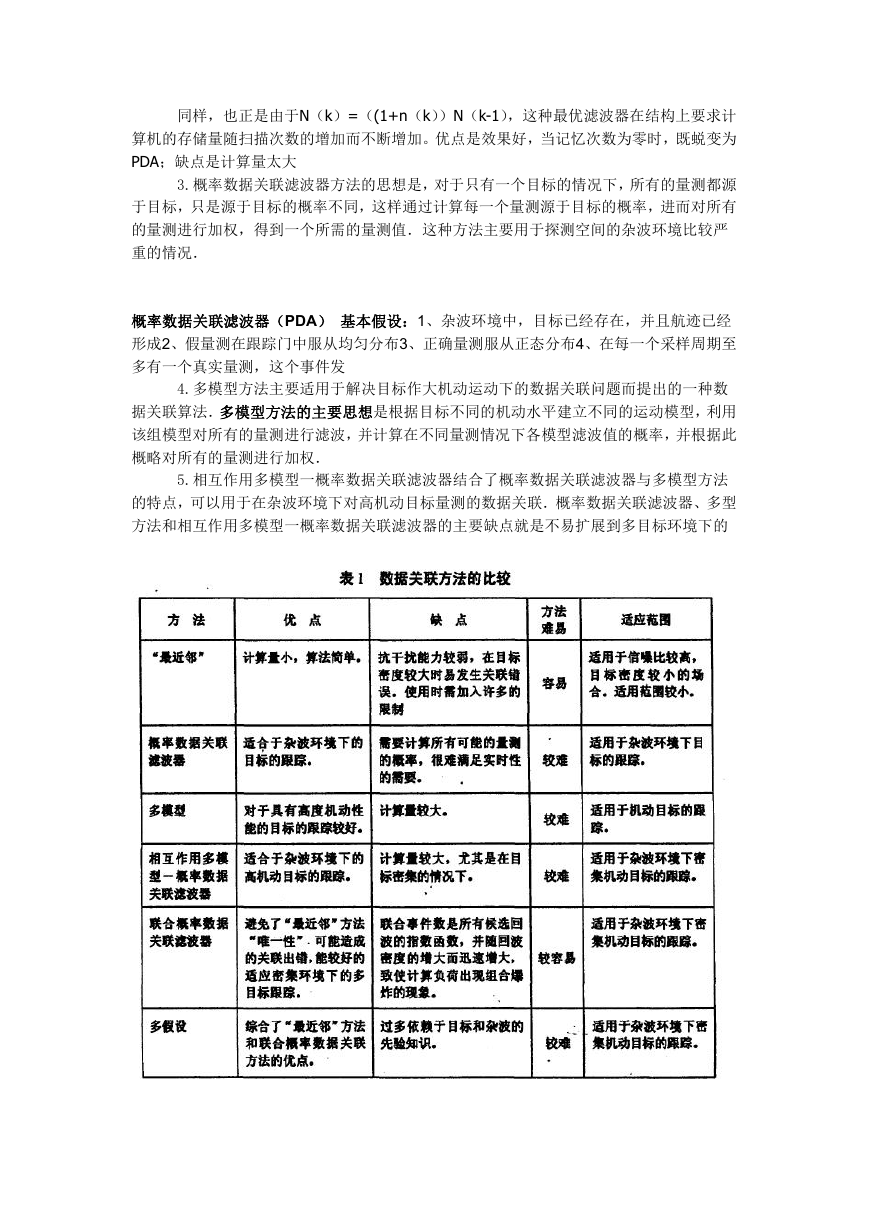
多目标跟踪的基本理论 所谓多目标跟踪，就是为了维持对多个目标当前状态的估计而对所接收到的量测信息进 行处理的过程。 目标模型不确定性 是指目标在未知的时间段内可能作己知的或未知的机动。一般情况下，目标的 非机动方式及目标发生机动时的不同的机动形式都可以通过不同的数学模型来加 以描述。在进行目标跟踪过程中，采用不正确的目标运动模型会导致跟踪系统跟踪 性能的严重下降。因而在目标跟踪过程中，运动模型采用的正确与否对目标的跟踪 性能是至关重要的。 观测不确定性 是指由传感器系统提供的量测数据可能是外部的干扰数据，它有可能是由杂波、虚警和 相邻的目标所引起的，也可能是由被跟踪目标的对抗系统所主动发出来的虚假信息。这种不 确定性在本质上显然是离散的，给目标跟踪问题提出了极大的挑战，相应地也就产生了数据 关联的问题。 数据关联 数据关联的作用主要有：航迹保持、航迹建立和航迹终结。 数据关联算法主要有：“最近邻”方法，“全邻”最优滤波器方法、概率数据关联滤 波器方法、多模型方法、相互作用多模型一概率数据关联滤波器方法、联合概率数据关联滤 波器方法、多假设方法、航迹分裂方法。 1.“最近邻”方法的思想是：在落入跟踪波门中的所有量测中，离目标跟踪预测位置最 近的量测认为是有效量测。“最近邻”方法的好处是算法最简单，但是精度差，抗杂波干扰 的能力差。“最近邻”方法因为简单，算法易实现，因此也是目前广泛采用的一种数据关联 算法． 2 .“全邻”最优滤波器 Singer,Sea 和 Housewright 发展了一类“全邻”滤波器，这种滤波器不仅考虑了所有候选 回波（空间累积信息），而且考虑了跟踪历史，即多扫描相关（时间累积信息）假定多余回 波互不相关并且均匀分布于跟踪门内，则任何跟踪门的体积 V 内多余回波的数目 Cx 服从均 值为βV 的泊松分布。假定在 K-1 时刻，轨迹 a′正确的概率为 Pa(k-1)。 关键问题是计 算 k 时刻轨迹的正确概率 Pa(k)。 

同样，也正是由于N（k）=（(1+n（k））N（k-1），这种最优滤波器在结构上要求计 算机的存储量随扫描次数的增加而不断增加。优点是效果好，当记忆次数为零时，既蜕变为 PDA；缺点是计算量太大 3.概率数据关联滤波器方法的思想是，对于只有一个目标的情况下，所有的量测都源 于目标，只是源于目标的概率不同，这样通过计算每一个量测源于目标的概率，进而对所有 的量测进行加权，得到一个所需的量测值．这种方法主要用于探测空间的杂波环境比较严 重的情况． 概率数据关联滤波器（PDA） 基本假设：1、杂波环境中，目标已经存在，并且航迹已经 形成2、假量测在跟踪门中服从均匀分布3、正确量测服从正态分布4、在每一个采样周期至 多有一个真实量测，这个事件发 4.多模型方法主要适用于解决目标作大机动运动下的数据关联问题而提出的一种数 据关联算法．多模型方法的主要思想是根据目标不同的机动水平建立不同的运动模型，利用 该组模型对所有的量测进行滤波，并计算在不同量测情况下各模型滤波值的概率，并根据此 概略对所有的量测进行加权． 5.相互作用多模型一概率数据关联滤波器结合了概率数据关联滤波器与多模型方法 的特点，可以用于在杂波环境下对高机动目标量测的数据关联．概率数据关联滤波器、多型 方法和相互作用多模型一概率数据关联滤波器的主要缺点就是不易扩展到多目标环境下的