中国科技论文在线 http://www.paper.edu.cn 神经网络系统辨识法综述 张国钧，李岚 太原理工大学信息工程学院，太原（030024） E-mail: lilan3207@163.com 摘 要：随着系统辨识技术发展的逐渐成熟，人工神经网络的系统辨识方法也越来越多的应 用于各个领域，本文首先将神经网络系统辨识方法与经典辨识法相比，总结出它的优越性， 然后再通过几种改进后的算法具体对其加以说明，最后展望了神经网络系统辨识法的未来发 展前景。 关键词：神经网络，系统辨识，系统建模 1 引言 L.A.Zadeh 曾给辨识下过这样的定义[Zadeh,1962]：“辨识就是在输入和输出数据的基础上， 从一组给定的模型类中，确定一个与所测系统等价的模型。”这明确说明了辨识的三个基本 要素:合适的模型、合适的观测数据和合适的评价准则。而 1978 年,L.Ljung 给辨识下的定义 则更加实用:“辨识有三个要素——数据,模型类和准则。辨识就是按照一个准则在一组模型类 中选择一个与数据拟合得最好的模型。”综上所述，辨识的实质可以归结为：从一组模型类 中选择一个模型,按照某种准则,使之能最好地拟合所关心的实际过程的静态或动态特性。 如今，经典的系统辨识方法的发展已经比较成熟和完善,包括阶跃响应法、脉冲响应法、 频率响应法、相关分析法、谱分析法、最小二乘法和极大似然法等。其中最小二乘法(LS) 是 一种经典的和最基本的,也是应用最广泛的方法。但随着人类社会的发展进步,越来越多的实 际系统很多都是具有不确定性的复杂系统。而对于这类系统,经典的辨识建模方法难以得到 令人满意的结果,即就是说,经典的系统辨识方法还存在着一定的不足: (1) 利用最小二乘法的系统辨识法一般要求输入信号已知,并且必须具有较丰富的变化, 然而,这一点在某些动态系统中,系统的输入常常无法保证； (2) 极大似然法计算耗费大，可能得到的是损失函数的局部极小值； (3) 经典的辨识方法对于某些复杂系统在一些情况下无能为力。 而随着科技的发展，人们发现人工神经网络具有良好的非线性映射能力、自学习适应能 力和并行信息处理能力,为解决未知不确定非线性系统的辨识问题提供了一条新的思路。所 以，神经网络系统辨识方法成为20 世纪末迅速发展起来的一门高等技术，并已经在各个领 域得到了广泛地应用。 本文首先介绍神经网络系统辨识法的概念，并与其他经典辨识法进行比较，接着结合几 个工程项目实例具体讲解神经网络系统辨识法的应用，最后指出神经网络这种系统辨识法的 前景。 2 神经网络系统辨识法 2.1 神经网络系统辨识法的定义 在神经网络辨识中,神经网络(包括前向网络和递归动态网络) 将确定某一非线性映射的 问题转化为求解优化问题,而优化过程可根据某种学习算法通过调整网络的权值矩阵来实现, 从而产生了一种改进的系统辨识方法。在辨识非线性系统时，人们可以根据非线性系统的神 经网络辨识结构,利用神经网络所具有的对任意非线性映射的任意逼近能力来模拟实际系统 -1- 

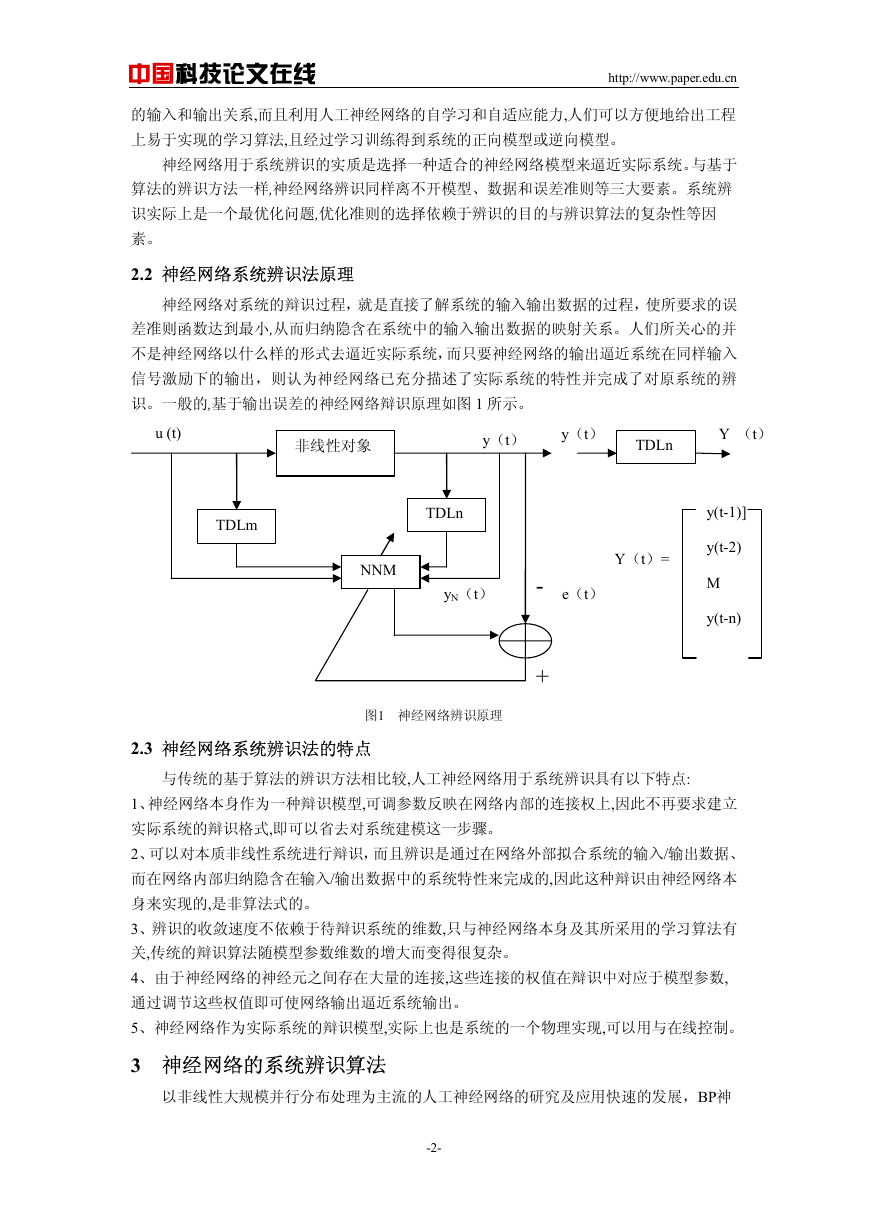
中国科技论文在线 http://www.paper.edu.cn 的输入和输出关系,而且利用人工神经网络的自学习和自适应能力,人们可以方便地给出工程 上易于实现的学习算法,且经过学习训练得到系统的正向模型或逆向模型。 神经网络用于系统辨识的实质是选择一种适合的神经网络模型来逼近实际系统。与基于 算法的辨识方法一样,神经网络辨识同样离不开模型、数据和误差准则等三大要素。系统辨 识实际上是一个最优化问题,优化准则的选择依赖于辨识的目的与辨识算法的复杂性等因 素。 2.2 神经网络系统辨识法原理 神经网络对系统的辩识过程，就是直接了解系统的输入输出数据的过程，使所要求的误 差准则函数达到最小,从而归纳隐含在系统中的输入输出数据的映射关系。人们所关心的并 不是神经网络以什么样的形式去逼近实际系统，而只要神经网络的输出逼近系统在同样输入 信号激励下的输出，则认为神经网络已充分描述了实际系统的特性并完成了对原系统的辨 识。一般的,基于输出误差的神经网络辩识原理如图 1 所示。 u (t) 非线性对象 y（t） y（t） TDLn Y （t） TDLm TDLn NNM yN（t） - e（t） Y（t）= + 图1 神经网络辨识原理 y(t-1)] y(t-2) M y(t-n) 2.3 神经网络系统辨识法的特点 与传统的基于算法的辨识方法相比较,人工神经网络用于系统辨识具有以下特点: 1、神经网络本身作为一种辩识模型,可调参数反映在网络内部的连接权上,因此不再要求建立 实际系统的辩识格式,即可以省去对系统建模这一步骤。 2、可以对本质非线性系统进行辩识，而且辨识是通过在网络外部拟合系统的输入/输出数据、 而在网络内部归纳隐含在输入/输出数据中的系统特性来完成的,因此这种辩识由神经网络本 身来实现的,是非算法式的。 3、辨识的收敛速度不依赖于待辩识系统的维数,只与神经网络本身及其所采用的学习算法有 关,传统的辩识算法随模型参数维数的增大而变得很复杂。 4、由于神经网络的神经元之间存在大量的连接,这些连接的权值在辩识中对应于模型参数, 通过调节这些权值即可使网络输出逼近系统输出。 5、神经网络作为实际系统的辩识模型,实际上也是系统的一个物理实现,可以用与在线控制。 3 神经网络的系统辨识算法 以非线性大规模并行分布处理为主流的人工神经网络的研究及应用快速的发展，BP神 -2- 

中国科技论文在线 http://www.paper.edu.cn 经网络完全可以用于非线性系统辨识。BP 网络(Back Propagation Network) 称为误差反向传 播神经网络,它是一种能朝着满足给定的输入/ 输出关系方向进行自组织的神经网络, 它由 三部分组成:输入层、隐含层、输出层,三部分之间通过各层节点之间的连接权依次前向连接。 目前,在人工神经网络的实际应用中,决大部分的神经网络模型是采用BP 网络和它的变化形 式,它也是前馈型网络的核心部分,并体现了人工神经网络最精华的部分。BP 网络主要应用 于函数逼近、模式识别、分类以及数据压缩中。 BP 网络用于函数逼近就是用输入矢量和相应的输出矢量训练一个网络逼近一个函数, 即可实现从输入到输出的任意的非线性映射。用于非线性系统辨识的三层BP 神经网络 x ( x x , 0 = ' ANN(n2m21) , 假设输入向量为 ，网络的输出为y 。记输入层与第二层间的连接权为 ijw ，阈值 x 为 jθ ， 第二层与输出层间的连接权为 jw ，阈值为θ，则每个层神经元的输出满足： ，中间隐层的输出向量为 x x , x − ,..., ( ) = ' 1 ' 1 m T 0 1 ' ,..., 1 x − n T ) y = f ⎛ ⎜ ⎝ m 1 − ∑ j x ' j = f ' ⎞ w x θ − ⎟ ⎠ j j n 1 − ∑ i = 0 w x θ − ij i j ⎞ ⎟ ⎠ 其中， j = 0,1,..., m 1 − 0 = ⎛ ⎜ ⎝ 对于总数为 h 个样本,按 δ 学习律,如果第 p 个样本 差为: n E p y −∑总 = t 1 2 p 1 = ( px 网络,得到输出 py ,则其总误 p )2 其中 pt 为教师值。 故E总为一个有关权 sqw 的非线性误差函数。BP 网络的训练过程也就是优化问题 w E 总 的求解过程。 min BP 算法的改进主要有两种途径,一种是采用启发式学习方法,如带动量的梯度算法,可看 作是共轭梯度法的近似;另一种是采用更有效的优化算法,如共轭梯度法和牛顿法等。以下为 列举的几种改进的算法。 3.1 基于混合混沌优化法的 BP 神经网络算法 由于传统的BP 神经网络关于权的学习算法普遍采用单纯的梯度法进行权的优化处理, 难免会使网络在学习过程中陷入局部最优的尴尬局面,从而影响神经网络权的训练和收敛速 度,所以有必要对网络训练的算法进行再研究。 混沌是非线性系统所独有且广泛存在的一种非周期的运动形式,表现出介于规则和随机 之间的一种行为。禁忌搜索法(tabu search , TS) 是一种全局逐步寻优的搜索算法,通过记忆能 -3- 

中国科技论文在线 http://www.paper.edu.cn 力和期望准则达到搜索解空间的目的。利用混沌所具有的搜索全局的能力和禁忌搜索法的 “记忆”能力,建立混合混沌优化算法。在BP神经网络的训练过程中,结合混合混沌优化法使总 误差E 总 达到最小,可得基于混合混沌优化法的BP 神经网络。 优化后的算法汲取了混合混沌优化法的优点,避免了网络训练过程中陷入局部最优的可 能性,且具有较强的非线性逼近性能、预测能力和分类判断能力、训练过程快速,算法简单, 有利于误差控制，所以具有很好的实际应用价值。 3.2 基于 LM 算法的神经网络系统辨识 LM 算法是一种利用标准的数值优化技术的快速算法,它是梯度下降法与高斯- 牛顿法 的结合,也可以说成是高斯- 牛顿法的改进形式,它既有高斯- 牛顿法的局部收敛性,又具有梯 度下降法的全局特性。它的形式为: 1 − Δ J T x ( ) 0μ> 为常数,I 是单位矩阵。如果比例系数 0μ= ,则为高斯- 牛顿法;如 该式中比例系数 果μ取值很大,则LM 算法接近梯度下降法, 每迭代成功一步,则μ减小一些,这样在接近误 差目标的时候,逐渐与高斯-牛顿法相似。 Iμ ( ) x ( ) x + J ⎡ ⎣ J ( ) x e x = − ⎤ ⎦ 由于LM 算法利用了近似的二阶导数信息,它比梯度下降法快得多,实践证明,采用LM 算法可以较原来的梯度下降法提高速度几十甚至上百倍,在精度和稳定性上也有很大的提高, 且辨识效果也相当理想,在非线性系统建模中具有非常广阔的应用前景。 4 结束语 目前，人工神经网络已经在各个领域得到了广泛地应用,尤其是在智能系统中的非线性 建模及控制器的设计、模式分类与模式识别、联想记忆和优化计算等方面得到了人们的极大 兴趣。因此，人工神经网络在非线性系统辨识中的应用具有很重要的研究价值和广泛的应用 前景。 参考文献 [1] 何玉斌,李新忠. 神经网络控制技术及其应用[M]. 北京:科学出版社, 2000. [2] K. S. Narendra & K. Parthasarathy, Identification and Control for Dynamical Systems Using Neural Networks IEEE Trans. Neu2ralNetworks,Vol. 1,No. 1, 4 - - 27, 1990. [3] 潘巨辉. 非线性系统辨识及其仿真研究——应用神经网络方法[ J ]. 计算仿真. No. 2 32 - 38, 1993. [4] 焦李成. 神经网络计算[M]. 西安:西安电子科技大学出版社,1993. [5] 胡守仁. 神经网络应用技术[M]. 长沙:国防科技大学出版社,1993. [6] Lippman R P. An Introduction to Computing with Neural Net [J ] . IEEE ASSP Magazine ,1989 ,4 (2) :4 - 22. [7] Venugopal K P ,Pandya A S. Alopex Algorithm for Training Multilayer Neural Networks [ C ] . IEEE Int . Conf . onNN ,1991 ,21 (2) :196 - 201. [8] Montana D J ,Davis L. Training Feedforward Network Using Genetic Algorithms [ C] . Int . J . Conf . on AI ,1989 ,32(5) :762 - 767. [9] Singhal S ,Wu L. Training feed - forward networks with the extended Kalman algorithms[C] . IN : Proc. of the IEEE Int . Conf .on Acoustics , Speech and Signal Processing ,Glasgow ,1989 :1 187 - 1 190. [10] 赵 弘,周瑞祥,林廷圻. 基于 Levenberg-Marquardt 算法的神经网络监督控制. 西安交通大学学报. 2002, 36(5): 523-527. [11] 杨 德. 简论非线性系统的神经网络辨识. 运城学院学报 Vol. 23 No. 2, 2005. [12] 徐小平 ,王 峰,胡 钢. 系统辨识研究的现状. 自动化技术. 1004 - 373X(2007) 15 - 112 – 05. [13] 张伟标. 基于混合混沌优化法的 BP 神经网络算法. 上海工程技术大学学报. Vol. 18 No. 1, 2004. [14] 黄豪彩,黄宜坚, 杨冠鲁. 基于 LM 算法的神经网络系统辨识. 自动化技术. 1001 - 2265 (2003) 02 - 0006 – 04. -4- 

中国科技论文在线 http://www.paper.edu.cn [15] 王永骥, 涂 键.神经网络控制. 北京:机械工程出版社,1998. [16] 闻 新,周 露, 王丹力. MATLAB 神经网络应用设计. 北京:科学出版社,2000. [17] 易继锴,侯媛彬. 智能控制技术[M]. 北京:北京工业大学出版社,1999. [18] 李孝安. 一种基于遗传算法与进化编码的系统辨识方法[J]. 控制与决策. 1996,11(3) :404-407. [19] 李红 星. 基于遗传算法的闭环系统辨识方法[J]. 电气传动. 2000,31(3) :57-60. [20] 李茶玲,孙德保.遗传算法在系统辨识中的应用[J]. 华中理工大学学报. 1998,26(7) :57-58. [21] 徐丽娜,李琳琳.遗传算法在非线性系统辨识中的应用研究[J]. 哈尔滨工业大学学报. 1999,31(2) :39-42. [22] 吴广玉.系统辨识与自适应[M]. 哈尔滨:哈尔滨工业大学出版社,1987. [23] Zadeh L A .From Circuit Theory to System Theory[J]. Proc. IRE, 1962 ,50(5) : 856 - 865. [24] Leec H, Tengc C. Identification and Control of Dynamic Systems Using Recurrent Fuzzy Network [J].IEEE Trans. On Fuzzy Systems ,2000 ,8(4) :349 -366. [25] Kreinovich V ,Sirisaengtaksin O ,Cabrera S. Wavelet Neural Networks are Asymptotically Optimal Approximators for Functions of One Variable[C].IEEE Int.Conf.on Neural Networks,2002:2 174- 2 179. A Survey on Neural Network of System Identification Zhang Guojun, Li Lan Taiyuan University of Technology, Taiyuan (030024) Abstract With the development of the System Identification, the application of the Neural Network of System Identification is more and more. This paper firstly compares the Neural Network with the Traditional System Identification and summarizes the superiorities of the Neural Network, secondly illuminates concretely by some correct Algorithms to demonstrate its superiorities, finally points out its future development. Key words: neural network, system identification, system modeling 作者简介： 张国钧，男，1956 年生，副教授，主要研究方向是工业控制系统的分析与应用。 李岚，女，1984 年生，硕士研究生，主要研究方向是模式识别、工业控制系统的分析与应 用。 -5-