logo资料库

格子Boltzmann方法处理复杂边界.pdf

发布时间：2022-06-13 发布人：admin 分类：说明书 资料大小：1.03M 资料格式：pdf 举报 版权申诉
第1页 / 共10页
第2页 / 共10页
第3页 / 共10页
第4页 / 共10页
第5页 / 共10页
第6页 / 共10页
第7页 / 共10页
第8页 / 共10页
资料共10页，剩余部分请下载后查看
    第37卷 第4期 力 学 季 刊 Vol.37 No.42016年12月 CHINESE QUARTERLY OF MECHANICS Dec. 2016 doi: 10.15959/j.cnki.0254-0053.2016.04.001 收稿日期： 2016-11-18 基金项目： 作者简介： 国家自然科学基金(91441104)；上海市教育委员会科研创新项目(14YZ038) 薛海虹(1967−)，女，上海人，博士．研究方向：心血管．Email: haihong_xue@163.com 通信作者： 钱跃竑．Email: yuehongqian@126.com 格子Boltzmann方法处理复杂边界新进展 薛海虹1，王政道2，钱跃竑2 (1．上海交通大学 新华医院，上海 200092；2．上海大学 理学院力学所，上海 200072) 摘要：格子玻尔兹曼方法是相对较新的计算流体力学方法，具有其独特的优点，如自然并行计算以及复杂边界的处理．在日益重要的高性能计算上，将发挥越来越大的作用．在已经较为成熟的计算模型基础上，为计算复杂几何边界对流场的作用，大量学者提出了各类针对格子玻尔兹曼方法的边界处理格式．边界处理方式对计算的影响主要有三个方面：计算精度，算法稳定性以及并行性．本文简单介绍格子玻尔兹曼方法在边界处理上的一些最新进展．并通过对实际算例的计算比较各类边界处理方式的优劣． 关键词：计算流体力学；并行计算；流-固耦合 中图分类号：O357 文献标志码：A 文章编号：0254-0053(2016)04-0615-10 Recent Progress on Complex Boundary Treatments for Lattice Boltzmann Method XUE Hai-hong1, WANG Zheng-dao2, QIAN Yue-hong2 (1. School of Medicine, Shanghai Jiao Tong University, Shanghai 200092, China; 2. College of Science, Shanghai University, Shanghai 200072, China) Abstract: Lattice Boltzmann Method is a relatively new method in computational fluid dynamics. It possesses some intrinsic advantages over traditional methods, for example, inherent capability for parallel computing and great convenience in treating complex boundaries. With the increase of the importance for supercomputing, lattice Boltzmann method will play a more and more important role. The calculation model has been relatively mature. Considering the effect of complex geometric boundary, a large number of scholars put forward various boundary treatment in lattice Boltzmann method. The influence of boundary treatment for computing mainly lies in three aspects: accuracy, stability and parallelism. In this paper, we will give a brief review for the recent progress of lattice Boltzmann method for treating complex boundary conditions. We make a comparison about the advantages and disadvantages of other kinds of boundary treatments, through some calculations of some typical examples. Key words: computational fluid dynamics; parallel computing; fluid-solid interactions 流体力学研究如何准确预测流体对于物体的作用，无论对工程应用还是生活实践都有很大的指导意义．流体力学的最基本问题是求解著名的Navier-Stokes方程，加上合适的初始条件和边界条件．在一般情况下，对于稳态流动或者准稳态流动，初始条件对于流动终态的影响不大．对依赖初始条件的流动，初始条件一般由测量给出．边界条件的处理，在流场的求解当中有着重要的地位．对于固体和流体的接触面，我们一般将其处理为无滑移边界，在微流动中，固壁边界通常会参照实验结果处理为部分滑移边界．
    616 力学季刊 第37卷 但是，上述方程的精确解却难以求得．一般地，学术界通过三类方式指导实践：理论分析、实验测量和数值模拟．理论分析方面，由于上述控制方程为非线性方程，直接求解方程的难度非常大，只有一些极为特殊的条件下能够，求得精确解，一般研究人员会采用一些近似方法，如采用小参量摄动展开，或者新发展起来的同伦分析法等．实验方面，利用量纲分析等手段，抓住主要问题，忽略次要问题，将模型合理缩放，进行实验，从而对所关心结果进行预测．为了减少缩放带来的误差，有时会进行全尺寸的实验模拟．当然，一般而言，这样的实验耗资都非常高昂．数值模拟方面，研究人员通过各种方式，用计算机对上述方程进行求解，从而对实际情况进行求解．数值模拟的成本较低，一套算法开发出来之后，依照求解对象，修改参数，就可以对所关心的工况进行模拟．所以数值模拟在优化方面有着不可替代的优势．当然，其可行范围受多个参数影响，其精度、稳定性也有很大限制．一般而言，采用数值模拟设计出的最终结果，还需要实验验证后才会较可信地应用到实践指导中去． 数值模拟的可靠性直接涉及到设计成本．为降低成本，需要采用可信度较高的计算方法．传统的计算流体力学方法建立在网格基础之上，计算结果强烈地依赖于网格的质量．对于动边界的问题，网格往往难以随体运动．变形网格、滑移网格、嵌套网格等多种处理动边界的网格技术不断被提出．但是，仍然会出现网格重叠、交错等问题，而且网格质量难以保证．不同类型网格的交接面上还非常容易出现非物理现象．然而在实际工况的计算中，固壁边界的几何结构和运动的复杂性往往会影响到网格质量．例如在燃气涡轮发动机的模拟当中，涡轮机本身的结构较为复杂，加之转子在不同航速下，以不同的转速的高速旋转，使得还原真实情形的网格的构建十分困难．另外，发动机的噪音也是实际应用当中相当关注的一个问题．在传统的计算当中，由于湍流模型对流动的平均，在处理噪音的问题上，有从实验入手，通过对实验数据的分析，从而获得燃烧室产生的总声功率级的经验或估算公式[1-3]．也有需要加入适当的气动模型，然而现有的一些处理方法中，能够较为准确模拟的方法，在计算成本上比较高昂；而能够采用较少计算资源的计算方法在计算精度上又不尽人意[4]． 图1 航空燃气涡轮发动机典型结构 Fig.1 Typical structure of aviation gas turbine engine 格子Boltzmann方法，采用笛卡尔直角坐标系，不涉及网格的变形和运动．这避免了传动方法中计算对网格的依赖．另一方面，其算法的设计出发点是介观尺度的粒子行为，摆脱了流体力学对宏观连续介质的假设，在微尺度方面也有很好的表现．对于连续Boltzmann方程的求解，可结合各类不同的计算方法，得到多种不同的数值模拟方式，Qian等[5]于上世纪90年代初建立起来的格子Boltzmann方法结合了格子气自动机和Boltzmann方程两者的优点，能够快速、稳定地处理流动信息．格子气自动机是Hardy、Pomeau和Pazzis[6]最先提出的一种基于分子碰撞的四边形格子模型，即HPP模型．模型因缺乏足够的对称，于1986年由Frisch、Hasslacher和Pomea[7]改进，并提出了FHP模型，同时Wolfram[8]也独立提出了该模型．新模型基于六边形格子，建立了更为复杂的碰撞规则，具有更好的对称性．能满足质量、动量及能量的守恒，能够在宏观极限下得到N-S方程．为格子Boltzmann方法的建立提供了很好的参考． 以最经典的D2Q9模型为例，模型采用9个方向的离散速度来描述2维速度空间．平衡态方程定义为[5]
    第4期 薛海虹，等：格子Boltzmann方法处理复杂边界新进展 617 ()−++=αββαβααααδρ22221siissiieqiccccuucucwtxf, (1) 其中，ρ为密度，αu为速度，iw为权重系数，可通过质量(=ρif)、动量守恒(=ααρucfii)、动量通量守恒(+=αββαβαδρpuuccfiieqi)以及各向同性的条件求得 ====854103619194~~///iiiwi (2) 同时可以求得声速txcsδδ31=．通过Chapman-Enskog展开可将离散方程：()()()()[]txftxftxftttcxfeqiiiii,,,,αααααωδδ−−=++恢复至Navier-Stokes方程．并通过比较得到松弛因子ω和剪切粘性ν直接的关系：tcsδων−=2112．格子Boltzmann方法因其实现简便，并行化容易，因此在模拟应用中得到了广泛地应用．在实际工程应用中，边界条件的精度很大程度地决定了计算结果的可靠性．在过去的几十年中，前人在边界处理方面进行了大量的工作． 1 启发式边界处理方式 最初的依照介观概念提出的启发式边界处理方式是一类最简洁的边界处理方式．一般分为三类边界条件的处理：周期边界条件，滑移边界和无滑移边界． 图2 周期格式 Fig.2 Periodic scheme 周期边界条件要求从一侧流出的质量、动量从另一侧流入．上图给出该处理格式的示意图．由于该边界处理格式并没有引入系统外由于插值或是别的矫正而带来的误差，因此该边界能够有效回避各种由边界条件引起的精度问题和稳定性问题．其表达式可写成 ()()()()0,,,0,,',,',iiiLiLiifxctttfxtfxctttfxtααααααδδδδ++=++= (3) 其中，离散速度i的方向是指向等号右侧指向流场内部的方向．0表示左边界，L表示右边界．对于不需要考虑有限边界的工况，如：各向均匀湍流的演化、两相分离的模拟等，采用该边界无疑是首选．另外两种启发式边界格式分别是滑移格式和无滑移格式，均是从碰撞反弹(Bounce-back)模型发展而来，常用的还有图3中示意的半步长反弹(Half-way)格式以及修正反弹格式．以广泛使用的反弹格式为例，该计算格式要求碰撞至固体壁面的粒子质量相等，动量相反地反弹回来．由于壁面执行反弹时间上引入了一定的误差[9]，造成该格式精度较低．此后Ladd[10]改进了半步长碰撞反弹处理方式，引入了边界速度，其表
    618 力学季刊 第37卷 达式可写成 ()()22swiiiicucwtxfttxfααααρδ−=+,', (4) 其中，i表示方向i的反方向，wu表示壁面速度．该模型成功模拟了动边界问题． 图3 半步长反弹格式 Fig.3 Half-way bounce back scheme 然而，碰撞反弹处理方式的依旧存在着其模拟的边界只能在格点上或是格点中间的位置．这对复杂边界的模拟极其不利．为了解决这一问题，Verberg与Ladd[11-12]又引入了考虑体积分数的亚格子尺度(sub-grid-scale)模型，通过体积分数2α解决半满格子的问题，并模拟了真实大理石圆柱中的流动．于前人工作的基础上，Yin和Zhang[13]改变思路，通过插值得到格点中间处的速度来执行半步长反弹，用如下表达式表示 ()()>−−−<−−+=21221121232121λλλλλλααααα.,ffwfwmuuuuu (5) 其中各参数定义可见图4．该方法进一步改进了碰撞反弹格式．为了解决运动边界而造成的质量流失问题，2015年，Oulaid和Zhang[14]又在前述工作的基础上考虑了动边界中质量流失的问题，对质量进行了修正． 图4 曲边界参数示意图 Fig.4 Schematic illustration of interpolation treatment for curved boundary 2 插值密度分布函数的边界处理方式 这一类边界处理的方式是在边界处的格点上通过插值边界格点的质量密度分布函数，从而在执行碰撞迁移之后获得无滑移的边界条件．1998年Filippova和Hänel[15]首次采用了虚拟平衡态的方式考虑壁面
    第4期 薛海虹，等：格子Boltzmann方法处理复杂边界新进展 619 的精确位置，并且采用加密网格，对圆柱绕流问题进行了模拟．其插值函数如下 ()()()()()221swibisnibisnicuctxwtxftxftxfααααααρχχ,,,','*−+−= (6) 其中，*if是虚拟平衡态，其表达式为 ()()()−++=∗22422221sbsbisifisnicucuccuctxwtxfααααααρ,,* (7) 其中，**121:,2111121:,.2bbbuuuuuαααααλλχτλλλχλλτ−<==−−−≥=+= 因其稳定性不够理想，Mei等[16]在Filippova和Hänel的工作基础上，增加了一个点，扩大了其稳定性范围．采用如下参数选取 −=+−=≥−−==<τλχλλλλτλχλααααα12112121221,:,:**bbfuuuuu (8) 之后，Guo等[17]将密度分布函数分开平衡态和非平衡态两部分考虑，利用插值的方式将速度、密度、非平衡态部分的密度分布的数值插值到边界格点上．利用线性插值，可获得流体内第一临近点处的线性插值信息 ()bwsnφλλλφφ−−=11 (9) 其中wb/φ表示插值点或壁面处的速度αu． 然而在处理λ偏小，尤其是当0→λ时，壁面处的误差会被大幅放大．为解决这一问题，Guo等[17]引入流体内第二个点处的线性插值信息 ()fwsnφλλλφφ+−−+=11122 (10) 并将其同第一个点的信息，以加权的方式求得插值点的信息．通过加权系数的乘积来消除放大因子λ1．依照Guo等[17]，该较小的范围选取为0.75．最终，其表达式可表述为 ()()()()<−+≥=7501750211...,λφλλφλφφsnsnsnsn (11) 其中snφ可表示速度αu或非平衡态信息neqif．该方法在稳定性与精度上都取得了较好的结果，并成功模拟了同轴圆柱之间的Couette流．此后，Wang等[18]又在前述工作的基础上，考虑分段函数带来的稳定性和精度上的问题，摒弃了分段形式，提出了如下统一的插值格式
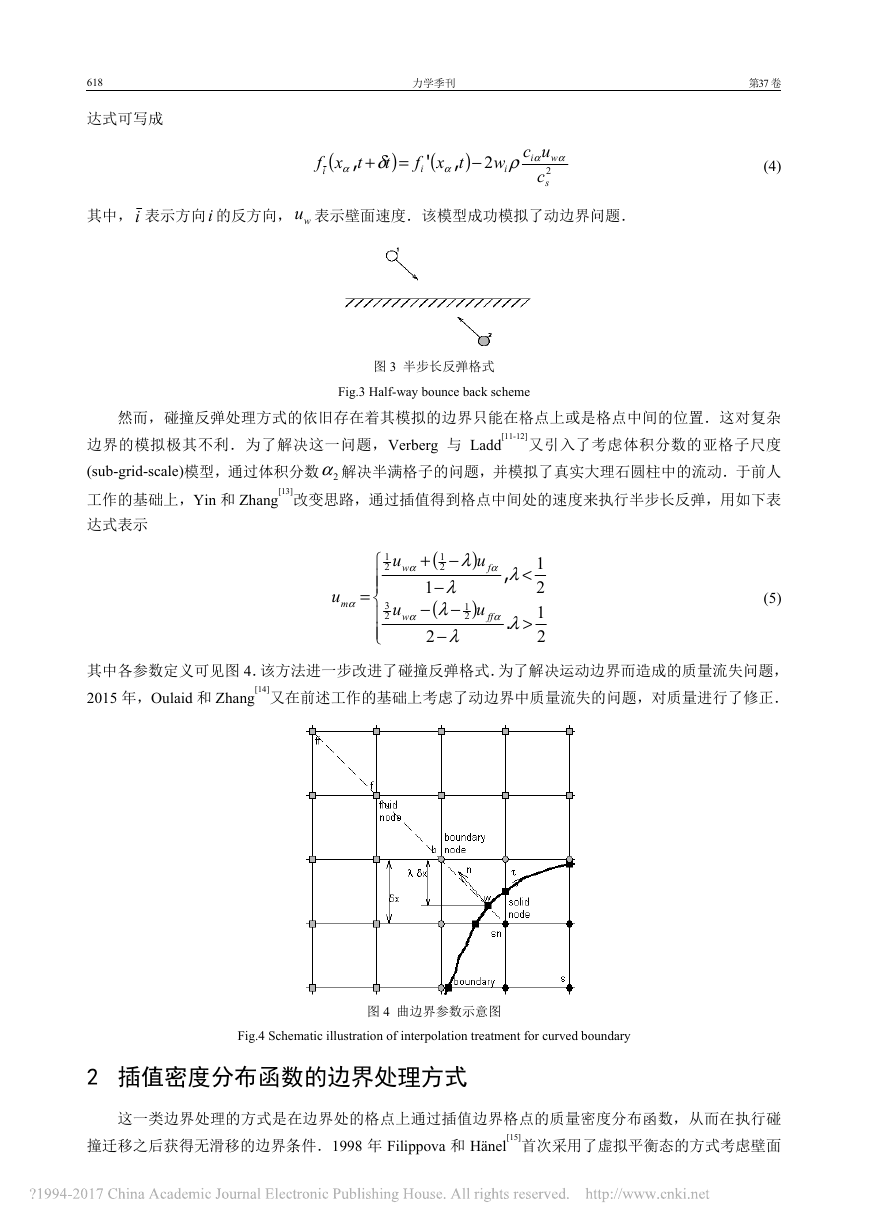
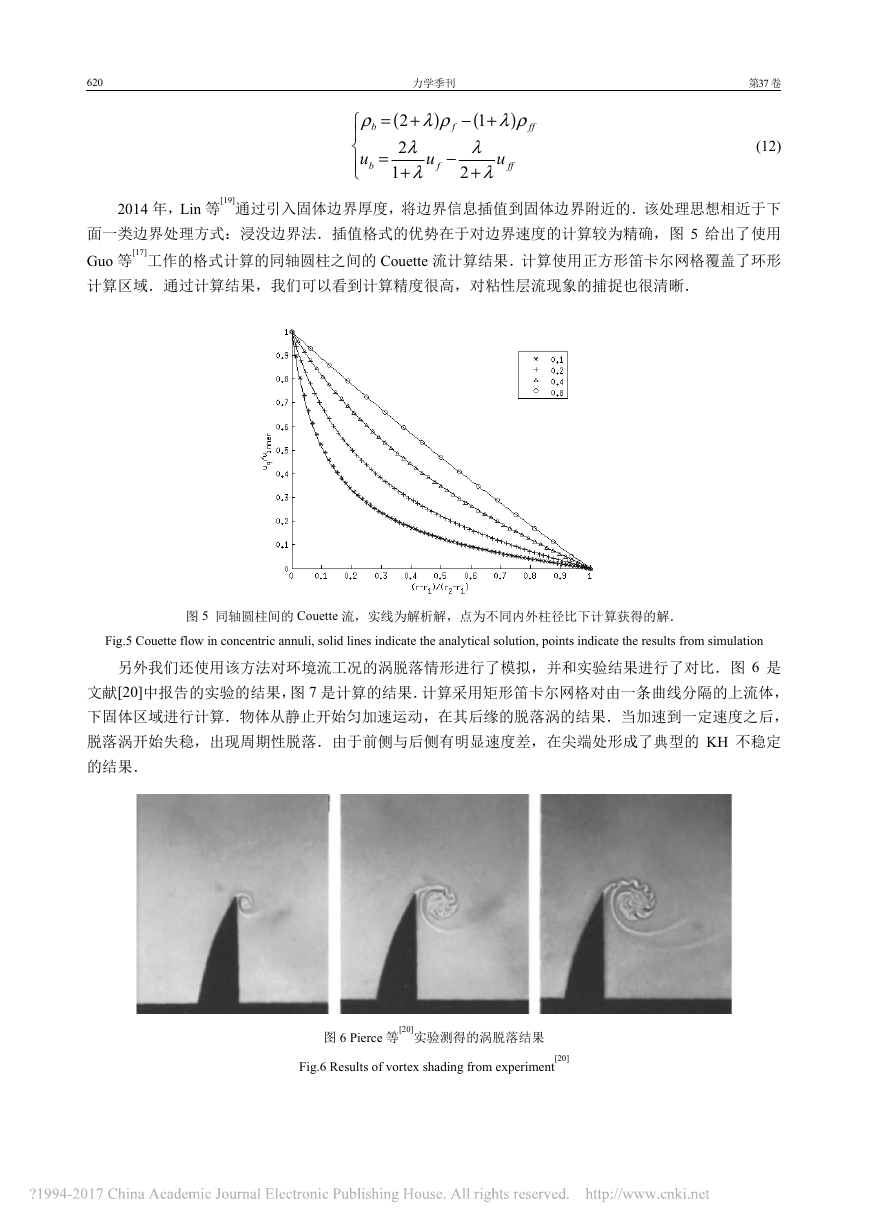
    620 力学季刊 第37卷 ()()+−+=+−+=fffbfffbuuuλλλλρλρλρ21212 (12) 2014年，Lin等[19]通过引入固体边界厚度，将边界信息插值到固体边界附近的．该处理思想相近于下面一类边界处理方式：浸没边界法．插值格式的优势在于对边界速度的计算较为精确，图5给出了使用Guo等[17]工作的格式计算的同轴圆柱之间的Couette流计算结果．计算使用正方形笛卡尔网格覆盖了环形计算区域．通过计算结果，我们可以看到计算精度很高，对粘性层流现象的捕捉也很清晰． 图5 同轴圆柱间的Couette流，实线为解析解，点为不同内外柱径比下计算获得的解． Fig.5 Couette flow in concentric annuli, solid lines indicate the analytical solution, points indicate the results from simulation 另外我们还使用该方法对环境流工况的涡脱落情形进行了模拟，并和实验结果进行了对比．图6是文献[20]中报告的实验的结果，图7是计算的结果．计算采用矩形笛卡尔网格对由一条曲线分隔的上流体，下固体区域进行计算．物体从静止开始匀加速运动，在其后缘的脱落涡的结果．当加速到一定速度之后，脱落涡开始失稳，出现周期性脱落．由于前侧与后侧有明显速度差，在尖端处形成了典型的KH不稳定的结果． 图6 Pierce等[20]实验测得的涡脱落结果 Fig.6 Results of vortex shading from experiment[20]
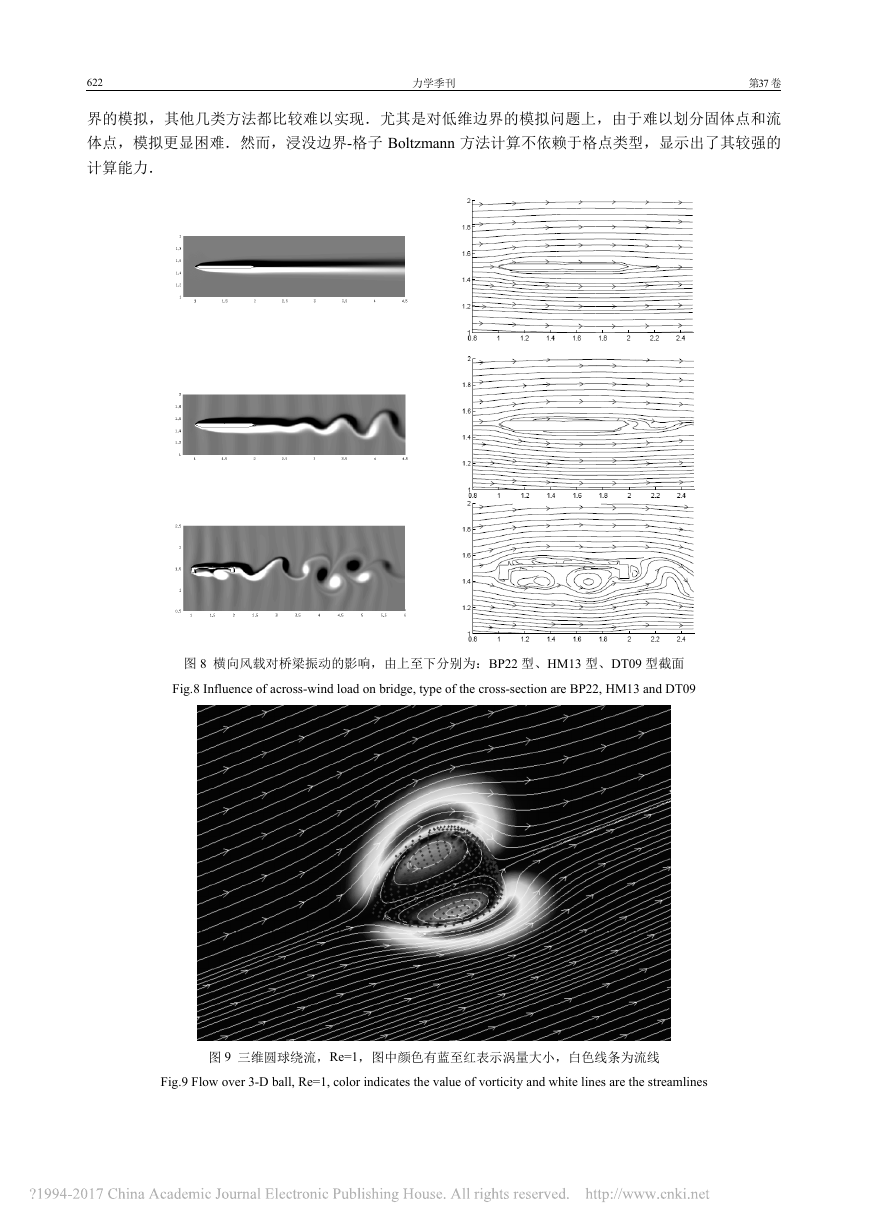
    第4期 薛海虹，等：格子Boltzmann方法处理复杂边界新进展 621 图7 计算获得的涡脱落结果 Fig.7 Results of vortex shading from simulation 3 浸没边界-格子Boltzmann方法 还有一种边界处理的方式是浸没边界与格子Boltzmann方法结合的处理方式(IB-LBM)．该类处理方法是将固体施加给流体的表面力从体力代替．通过保证边界处的无滑移条件，从而引入一个修正力．最初Feng和Michaelides[21]将浸没边界法与格子Boltzmann方法结合，通过可调的弹簧参数描述了一个与速度相关的修正力 ()tuukFwδααα−−= (13) 其中，弹簧参数02.=k．并成功模拟了颗粒沉降的问题．此后，Feng等[22]又在先前工作的基础上对修正力进行讨论，采用直接力模型描述该修正力 puuutuFααβαββααμρ∂+∂−∂+∂∂=2 (14) 并给出一种可行的离散模型 ()()()()()()nnnnnwnipuuutuuFααβαββααμδρ∂+∂−∂+−=++211 (15) 这种模型能够大大提高模拟精度和稳定性，但是对于极多边界点描述边界的情况，其计算量比起前者也将大大提高．之后，Niu等[23]考虑格子Boltzmann方法的特点，通过于边界点处交换的动量来计算修正力．该处理方式能够极大地满足复杂边界的任意性，然而，其中仍旧存在无法精确满足无滑移边界条件．此后，针对其精确度这一问题，Shu等[24]采用了插值速度的方式进行研究，将边界点处的速度通过线性插值取代δ函数来获得．Wu等[25]采用了隐式格式处理δ函数，对该类方法进行了改进，通过求解隐式方程ijijBXA=中系数矩阵ijA的逆矩阵来计算修正力的分布．其中，iiuXαδ=，()−Δ−=SiwiwisxxuuBδααααα，()()−Δ−Δ=SjjwiwijslxxxxAδδαα． 前述修正方法均取在计算中得了较好的结果．之后，Wang等[26]延续Shu等[24]的思路，通过二阶格式插值格点上的速度来计算修正力，并且成功模拟了鱼游和蜻蜓扑翼两种生物运动．2016年，Wang等[27]通过隐式格式计算修正力，并且将速度修正考虑在内，对3维圆球绕流进行了详细的模拟分析，获得了较好的结果．该类方法的优势在于对各种大变形复杂运动边界的处理上．图8为采用该类方法对三种典型桥梁甲板截面在一定参数下受横向风风载被迫振动的流场．图9为采用该类方法对三维圆球绕流在极低雷诺数(Re=1)的情况下进行的模拟得到的涡量流线图，红色点为球面上布的边界点．采用该类方法能够较容易地进行三维大规模并行计算．图10为对柔性绳在均匀流中扑动的情形．对于大变形低维动边界边
    622 力学季刊 第37卷 界的模拟，其他几类方法都比较难以实现．尤其是对低维边界的模拟问题上，由于难以划分固体点和流体点，模拟更显困难．然而，浸没边界-格子Boltzmann方法计算不依赖于格点类型，显示出了其较强的计算能力． 图8 横向风载对桥梁振动的影响，由上至下分别为：BP22型、HM13型、DT09型截面 Fig.8 Influence of across-wind load on bridge, type of the cross-section are BP22, HM13 and DT09 图9 三维圆球绕流，Re=1，图中颜色有蓝至红表示涡量大小，白色线条为流线 Fig.9 Flow over 3-D ball, Re=1, color indicates the value of vorticity and white lines are the streamlines
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料