第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
改进的遗传算法用于工业测量数据处理.doc
改进的遗传算法用于工业测量数据处理
潘国荣 1’2)，谷川 1)
⒈ 同济大学测量与国土信息工程系，上海 200092；
⒉ 现代工程测量国家测绘局重点实验室，上海 200092
摘 要：从遗传算法的两个缺陷入手，在几个方面对其进行改进，并且用 MATLAB语言编程
实现了改进后的算法。文章用一个工程实例，探讨了将改进后的遗传算法应用于工业测量和逆
向工程领域的可行性，并且通过比较发现改进后的算法在全局收敛以及收敛速度方面都有了较
大的改善，说明了文章所作的改进是有效的。文章提出的遗传算法的改进和应用的探讨具有较
好的实用价值。
关键词：遗传算法 改进 全局收敛性 收敛速度 工业测量 数据处理 马鞍面（双曲抛物面）
Application of Improved GA in Industrial Surveying Data Processing
PAN Guorong1, 2), GU Chuan1)
(⒈ Department of Surveying and Geo-informatics, Tongji University, Shanghai 200092; ⒉ Key Laboratory of Modern
Engineering Surveying, SBSM, Shanghai 200092)
Abstract: Viewing from two defects of traditional simple genetic algorithm, this paper modifies it
from several aspects, and realizes the improved algorithm using MATLAB language programming.
Using an engineering example, this paper discusses the feasibility of applying improved GA into
industrial surveying and reverse engineering. Through comparison, this paper finds out that the
improved GA has good betterment in global convergence and convergence rate, which reflects that the
improvement is effective. The improvement of GA and its application has good practicability.
Keywords: genetic algorithm,
surveying, data processing, hyperbolic paraboloid
1 引言
improvement, global convergence, convergence rate,
industrial
在工业测量以及逆向工程中，由于实物的形状通常有严格的数学公式描述，通过采集其表
面数据点的三维坐标，可以拟合出实物表面在空间三维坐标系中的几何方程，这对于发现实物
的整体变形以及生成模型设计CAD图纸是至关重要的。对于平面拟合问题，已经得到很好的解
决，但对于复杂曲面，即便是简单的二次曲面的最小二乘拟合的研究也相对较少，而且已有的
拟合算法存在方程求解问难、有奇异值和算法不稳定等问题[1]，因此一种好的全局优化算法就
显得极其必要。
遗传算法(Genetic Algorithm，简称GA)是由美国Michigan大学的John H. Holland教授于1975
年在他的著作《Adaptation in Natural and Artificial Systems》中根据C. R. Darwin的生物进化论和
G. Mendel的遗传变异理论提出的一种基于种群搜索的优化算法。其思想是随机产生初始种群,
通过选择(Reproduction)、交叉(Crossover) 和变异(Mutation) 等遗传算子的共同作用使种群不断
进化, 最终得到最优解[2]。
与其他优化方法相比，遗传算法以单一字符串的形式描述所研究的问题，只需利用适应度函数
进行优化计算, 而不需要函数导数等其他信息，特别适合解决其他学科技术无法解决或难以解
投稿日期：2008-01-12
基金项目 国家自然科学基金（40674010）;“十一五”科技支撑项目（2006BAC01B02-02-02, 05）
作者简介：潘国荣：教授、博士生导师，主要研究方向为精密工程测量、工业测量与测量数据
处理。Email: pgr2@163.com
决的复杂和非线性问题，是继专家系统、人工神经网络之后又一受人青睐的人工智能学科，一
直是研究的一个热点，被广泛地应用于组合优化、机器学习、自适应控制、规划设计、智能机
器系统、智能制造系统、系统工程，人工智能、人工生命等领域，是21世纪智能计算中的关键
技术之一[3]。
习惯上将John H. Holland提出的遗传算法称为简单遗传算法(Simple Genetic Algorithm, 简
称SGA)。和其它优化方法一样，由于全局性的要求，简单遗传算法作为一种通用的自适应随机
搜索算法，还存在着早熟收敛(过早收敛于局部最优值)和收敛速度慢这两个缺陷，而且比较难
克服,这给遗传算法的应用带来了很大的不便。
⒉ 遗传算法的改进
出现早熟往往是由于种群中出现了某些超级个体，随着模拟生物演化过程的进行，这些个
体的基因物质很快占据种群的统治地位，导致种群中由于缺乏新鲜的基因物质而不能找到全局
最优值；另一个主要原因是由于遗传算法中选择及杂交变异等算子的作用，使得一些优秀的基
因片段过早丢失，从而限制了搜索范围，使得搜索只能在局部范围内找到最优值，而不能得到
满意的全局最优值[4]。
Whitley认为，遗传算法中最重要的两个因素就是“种群多样性”和“选择压力”，而选择
压力过大是导致早熟收敛的一个重要原因。过大的选择压力虽然可以加快算法的收敛速度，却
会使种群中适应度不利于问题的求解的个体迅速“死亡”，种群的多样性遭到破坏，使得算法
搜索空间减小，进而导致算法错误地收敛到局部最优值。降低选择压力虽然可以增大算法搜索
到全局最优值的概率，但却会降低搜索效率，使算法的收敛速度变慢。为了使算法具有良好的
性能，必须在提高选择压力和保持种群多样性之间达到某种平衡[5]。
为提高遗传算法的搜索效率并保证得到问题的最优解，从以下几个方面对简单遗传算法进
行改进：
2.1 初始种群产生
在遗传算法中，采用实数编码策略比二进制编码策略具有精度高、搜索范围大、表达自然
直观等优点。如此，能克服二进制编码所存在的诸多缺点，如不易求解高精度问题、不便于反
应所求问题的特定知识及无法借鉴一些经典优化算法的宝贵经验等。
2.2 个体适应度计算
计算适应度，需先构造适应度函数。合理的适应度函数能引导搜索朝最优化方向前行。本
文的适应度函数是基于顺序的基础，其特点是个体被选择的概率与目标函数的具体值无关，仅
与顺序有关。构造方法是先将种群中所有个体按目标函数值的好坏进行排序，设参数β∈(0,1)，
定义基于顺序的适应度函数为：
eval
i=1,2,…m
1(
)
(1)
i
1
(
'
iX
)
iX 为种群个体按优劣排序后的第 i 个个体。β一般在 0.01~0.3 之间取值。
式中， '
2.3 选择与交叉
放弃赌轮选择，避免早期的高适应度个体迅速占据种群和后期的种群中因个体的适应度相
差不大而导致种群停止进化。此处采用基于种群的按个体适应度大小排序的选择算法代替赌轮
选择方法，其过程伪码描述如下：
fitsort()
{
将种群中的个体按适应度大小进行排序；
}
while(种群还没有扫描完) do
{
排在最前面的个体复制两份；
排在中间的个体复制一份；
排在后面的个体不复制；
}
在不破坏种群基因多样性的前提下加快算法的进化速度。
交叉率 Pc 按照公式(2)进行自适应调整：
'
f
f
f
f
1
k
Pc
max
max
k
2
ave
f
'
f
'
f
ave
f
ave
(2)
式中，fmax 为群体中最大的适应度值；fave 为每代群体的平均适应度值；f’为要交叉的两个个体中
较大的适应值。此处，只要设定 k1，k2（在[0，1]取值）的值，Pc 即可进行自适应调整。
2.4 个体子代的产生
在选择出父本和母本后，按照交叉方法（单点、多点、一致交叉）进行 n 次交叉，产生 2n
个个体，再从这 2n 个个体中选出最优的两个个体加入到新的种群中。如此，既保留了父本和母
本的基因，又在进化的过程中种群中个体的平均性能。
2.5 变异
在遗传算法中，如采用固定的变异概率 Pm，则当 Pm 取值很小时，变异算子对群体不会产
生影响，不利于新的基因的引入；而当 Pm 取值很大时，有可能破坏群体中的优良基因，使得
算法收敛速度变慢甚至不收敛。此处，本文采用动态确定变异概率的方法，该方法既可防止优
良基因因为变异而遭破坏，又可在陷入局部最优解时引入新的基因，该方法的伪码描述如下：
if 个体的适应度>平均适应度
then Pm 取值很小或为 0；
else
Pm 取值相对很大；
end if
如此，使得种群中好的基因不被破坏，既有利于不良基因的去除，又有利于新的基因的引
入，从而可以很大程度的提高遗传算法的性能。
具体的自适应调整的公式为：
Pm
k
3
k
4
f
f
max
max
f
f
ave
f
f
ave
f
f
ave
(3)
式中，fmax 为群体中最大的适应度值；fave 为每代群体的平均适应度值；f’为要变异个体的适应度
值。此处，只要设定 k3，k4（在[0，1]取值）的值，Pm 即可进行自适应调整
2.6 种群的进化与进化终止条件
将初始种群和产生的子代种群放在一起，形成新的种群，然后计算新的种群各个体的适应
度，将适应度排在前面的 m 个个体保留，将适应度排在后面 m 个个体淘汰，这样种群便得到了
进化。
每进化一次计算一下各个个体的目标函数值，当相邻两次进化平均目标函数之差小于等于
某一给定精度ε时，即满足如下条件：
(
XF
)1(
t
XF
(
t
)
(4)
式中，
)1(
tXF
(
为第 t+1 次进化后种群的平均目标函数值，
tXF
(
)
为第 t 次进化后种群的平均
目标函数值，此时，可终止进化。
2.8 遗传算法流程及编程实现
遗传算法流程的伪码表示为：
Procedure Genetic Algorithm;
begin
k=0;
初始化 P(k);
计算 P(k)的适应值；
while (不满足停止准则) do
begin
k=k+1;
从 P(k-1)中选择 P(k);{复制算子}
重组 P(k)；{杂交和变异算子}
计算 P(k)的适应值；
end
end
end
作者采用 MATLAB 编程语言，实现了本文提出的改进遗传算法的程序包[6]。为了证明其有
效性和探讨其用于工业测量和逆向工程领域求取复杂模型参数的有效性，采用了一个钢结构部
件表面方程拟合的工程实例来说明问题。
⒊ 改进遗传算法用于工业测量数据处理
某钢结构工业构件的表面为马鞍面（双曲抛物面），用工业测量的手段测得了其表面数
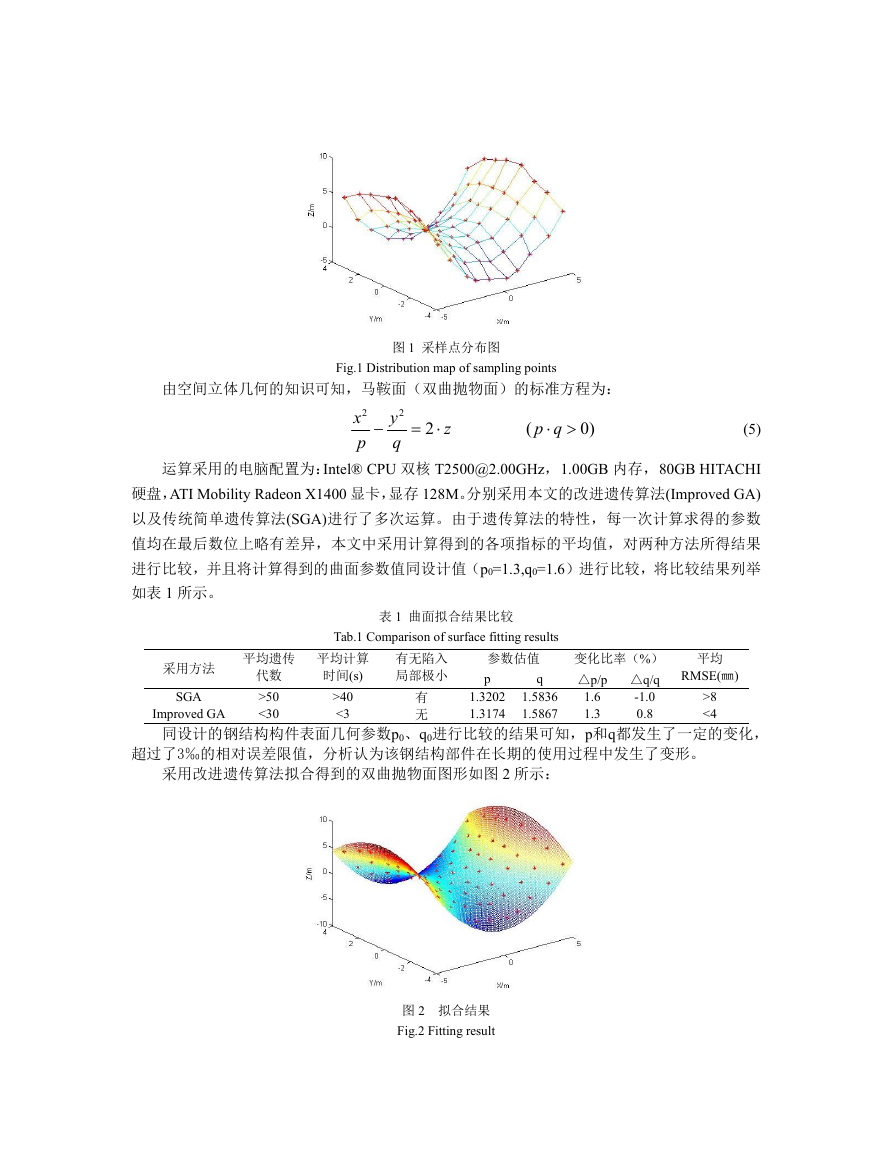
十个点的坐标，标记为(Xi, Yi, Zi)。由于工业测量系统采用的是与该构件相一致的坐标系统，故
无须进行旋转平移等操作。得到的测量点临近点相连接得到如图 1 所示的图形。
图 1 采样点分布图
Fig.1 Distribution map of sampling points
由空间立体几何的知识可知，马鞍面（双曲抛物面）的标准方程为：
2
x
p
2
y
q
2
z
(
qp
)0
(5)
运算采用的电脑配置为：Intel® CPU 双核 T2500@2.00GHz，1.00GB 内存，80GB HITACHI
硬盘，ATI Mobility Radeon X1400 显卡，显存 128M。分别采用本文的改进遗传算法(Improved GA)
以及传统简单遗传算法(SGA)进行了多次运算。由于遗传算法的特性，每一次计算求得的参数
值均在最后数位上略有差异，本文中采用计算得到的各项指标的平均值，对两种方法所得结果
进行比较，并且将计算得到的曲面参数值同设计值（p0=1.3,q0=1.6）进行比较，将比较结果列举
如表 1 所示。
采用方法
SGA
平均遗传
代数
>50
<30
表 1 曲面拟合结果比较
Tab.1 Comparison of surface fitting results
平均计算
时间(s)
有无陷入
局部极小
参数估值
p
q
>40
<3
有
无
1.3202
1.3174
1.5836
1.5867
变化比率（%）
△p/p △q/q
1.6
-1.0
0.8
1.3
平均
RMSE(㎜)
>8
<4
Improved GA
同设计的钢结构构件表面几何参数p0、q0进行比较的结果可知，p和q都发生了一定的变化，
超过了3‰的相对误差限值，分析认为该钢结构部件在长期的使用过程中发生了变形。
采用改进遗传算法拟合得到的双曲抛物面图形如图 2 所示：
图 2 拟合结果
Fig.2 Fitting result
⒋ 结语
本文针对遗传算法的两个缺陷从几个方面着手进行了改进，并且用一个钢结构工业构件表
面检测的工程实例说明了改进算法的有效性和探索其应用于工业测量和逆向工程的可行性。
通过文中的实例和比较结果发现，改进后的遗传算法在全局收敛性和收敛速度方面都有了
很大的改善，并且快速准确有效地求得复杂结构物体数学描述方程的参数，由此可以得出结论，
改进后的遗传算法具有很好的优势，并且完全可以应用于工业测量和逆向工程领域。
参考文献:
1 顾步云，周来水，刘胜兰，陈涛.逆向工程中二次曲面拟合方法的研究[J].南京：机械制造与研
究，2004 , 33 ( 1)：11-14.
1 Gu Buyun, Zhou Laishui, Liu Shenglan, Chen Tao.Study on algorithm of quadric surface fitting in
reverse engineering[J]. Nanjing: Machine Building & Automation, 2004 , 33 ( 1) : 11-14.
2 Holland J. Adaptation in natural and artificial systems[M].University of Michgan Press,1975.
3 王福林，王吉权，吴昌友，吴秋峰.实数遗传算法的改进研究[J].鞍山：生物数学学报，2006，
21（1）：153-158.
3 Wang Fulin, Wang Jiquan, Wu Changyou,Wu Qiufeng.The improved research on actural number
genetic algorithms. Anshan: Journal of Biomathematics, 2006，21(1): 153-158.
4 黄绪明.一类改进的遗传算法[J].长沙：长沙大学学报，2005，19（5）:1-4.
4 Huang Xuming. A kind of improved hereditary algorithm. Changsha, Journal of Changsha
University, 2005, 19(5): 1-4.
5 Whitley D. The genetic algorithm and selection pressure: why rank-based allocation reproduction
trials is best[A].In Schaffer J, Proceeding of the 3rd international conference on genetic algorithm[C].
Los Altos: Morgan Kaufmann publishers, 1989.
6 雷英杰，张善文，李续武，周创明. MATLAB遗传算法工具箱及应用[M].西安：西安电子科技
大学出版社，2005.
6 Lei Yingjie, Zhang Shanwen, Li Xuwu, Zhou Chuangming. MATLAB genetic algorithm toolbox
and application[M].Xi’an: Xidian Unversity Press, 2005.
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
