logo资料库

论文研究-复杂网络中节点重要度评估的节点收缩方法.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书 资料大小：0.31M 资料格式：pdf 举报 版权申诉
第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
资料共6页，全文预览结束
    2 2 　2006 年 11 月 文章编号 :1000 系统工程理论与实践 第 11 期 　 0079 05 6788 (2006) 11 复杂网络中节点重要度评估的节点收缩方法 谭跃进 ,吴 　俊 ,邓宏钟 (国防科技大学 信息系统与管理学院管理系 ,长沙 410073) 摘要 : 　首先定义了网络的凝聚度 ,在此基础上提出了一种评估复杂网络节点重要度的节点收缩方法 , 认为最重要的节点就是将该节点收缩后网络的凝聚度最大 ,其算法的时间复杂性为 O ( n3 ) . 该方法综合 考虑了节点的连接度以及经过该节点最短路径的数目 ,克服了节点删除法的弊端. 最后的实验分析表明 该方法直观 、有效且运算速度快 ,对于大型复杂网络可以获得理想的计算能力. 关键词 : 　复杂网络 ;凝聚度 ;节点重要度 ;节点收缩 中图分类号 : 　N949 　　　　　　　　文献标志码 : 　A 　　　 Evaluation Method for Node Importance based on Node Contraction in Complex Networks TAN Yue jin , WU Jun , DENG Hong zhong (Department of Management , School of 410073 , China) Information System and Management , National University of Defense Technology , Changsha Abstract : 　Complex networks with inhomogeneous topology are very fragile to intentional attacks on the“hub nodes”. It is very important and desirable to evaluate the node importance and find these “hub nodes”. The networks agglomeration is defined firstly. A node contraction method of evaluation of node importance in complex networks is proposed based on a new evaluation criterion ,i. e. the most important node is the one whose contraction results in the largest increase of the networks agglomeration. With the node contraction method ,both degree and position of a node are considered and the disadvantage of node deletion method is avoided. An algorithm whose time complexity is O(n3 ) is proposed. Final experiments verify its efficiency. Key words : 　complex networks ; agglomeration ; node importance ; node contraction 1 　引言 我们被网络包围着 ,几乎所有的复杂系统都可以抽象成网络模型 ,这些网络往往有着大量的节点 ,节 点之间有着复杂的连接关系. 随着复杂网络的小世界效应[1 ] 及无标度性[2 ] 的发现 ,复杂网络研究逐渐成为 多个学科共同关注的前沿热点[3 ,4 ] . 作为复杂网络的一个重要研究方向 ,复杂网络的容错抗毁性也随之兴 起[5～7 ] . 研究表明不同拓扑结构的网络对不同打击具有不同的抗毁性 ,在随机打击下无标度网络比随机网 络具有更强的容错性 ,但在选择性打击下 ,无标度网络却又显得异常脆弱 ,5 %的核心节点被攻击 ,网络就 基本瘫痪[5 ] . 所谓选择性打击就是先攻击网络中重要的“核心节点”,那么对复杂网络中节点的重要度进行 评估将是一项非常有意义的工作. 通过节点重要度评估找出那些重要的“核心节点”,一方面可以重点保护 这些“核心节点”来提高整个网络的可靠性 ,另外一方面也可以攻击这些“薄弱环节”达到摧毁整个网络的 目的. 相对于网络中边的重要度评估[8～10 ] ,网络中节点的重要度评估一直以来并未受到太多关注 ,现有的评 估方法很有限. 最简单地我们可以把节点的连接度 (节点连接的边数) 作为节点重要度的衡量标准[5 ] ,认为 收稿日期 :2005 资助项目 :国家自然科学基金 (70501032) 22 09 　　作者简介 :谭跃进 (1958 - ) ,男 ,博士生导师 ,主要研究方向为系统理论与综合集成 ;吴俊 (1980 - ) ,男 ,博士研究生 ,主 要研究方向为系统管理与综合集成 ,复杂网络理论 ;邓宏钟 (1974 - ) ,男 ,博士 ,主要研究方向为复杂系统理论 ,分布式人工 智能和遗传算法.
    08 系统工程理论与实践 2006 年 11 月 与节点相连的边越多则该节点越重要 ,显然这种评估方法具有片面性 ,有些重要的“核心节点”并不一定具 有较大的连接度 ,比如只有两条边相连的“桥节点”. 文献[ 11 ,12 ]中提出的介数 (betweenness centrality) 似乎 能很好地衡量节点的重要度 ,即经过该节点的最短路径越多该节点越重要 ,但计算节点的介数非常复杂 , 因为我们不仅要计算各个节点对之间的最短路径长度 ,还要记录这些最短路径的路线. 文献[ 13 ,14 ]基于 源点到汇点最短路径来评价节点重要度 ,定义最重要的节点为删除该节点使源点到汇点最短路径距离增 加最大. 文献[15 ]提出了一种基于生成树数目的节点删除法 ,定义最重要的节点为去掉该节点使得生成树 数目最小. 文献[13～15 ]都用到了节点的删除方法 ,即假设节点失效 ,通过比较删除节点前后网络性能的 变化来评估节点重要度. 节点删除法存在一个问题 ,就是如果多个节点的删除都使得网络不连通 ,那么这 些节点的重要度将是一致的 ,从而使得评估结果不精确. 例如 ,在很多实际复杂网络中都存在大量连接度 为 1 的“末梢节点”,如果这些“末梢节点”所依附的节点被删除 ,网络就不再连通 ,由此推断这些被依附节 点的重要度相同显然是不合理的. 本文提出了一个新的评估准则 ,即假设在节点正常工作的情况下 ,通过 收缩与该节点相连的边 ,认为收缩后得到的网络凝聚程度越高则该节点越重要 ,这样就克服了节点删除法 的上述弊端. 这种方法综合考虑了节点的连接度以及节点所处位置 ,直接评估了节点正常工作对网络的贡 献大小. 本文首先介绍了节点重要度评估的网络模型和假设 ,然后定义了网络的凝聚度 ,在此基础上给出了基 于凝聚度的节点收缩方法及其算法 ,最后通过实验分析验证了该方法的有效性. 2 　符号及假设 复杂网络可以用图 G = ( V , E) 来表示 ,其中 G 是一个无向的连通图 ,有 n 个节点 , m 条边 , V = { v1 , V ×V 代表边的集合. G 的邻接矩阵 H = [ hij ]有 n 行 v2 , v3 , …, vn }代表节点集合 , E = { e1 , e2 , e3 , …, em } n 列 , H 中元素 hij 定义如下 : hij = 1 , 第 i 个节点与第 j 个节点有边相连 0 , 第 i 个节点与第 j 个节点没有边相连 , (1) 对于图 G ,我们作如下假设 : 1) 所有节点和边的失效概率相同 ; 2) 节点只有两种状态 :正常和失效 ; 3) 节点的失效是相互独立的. 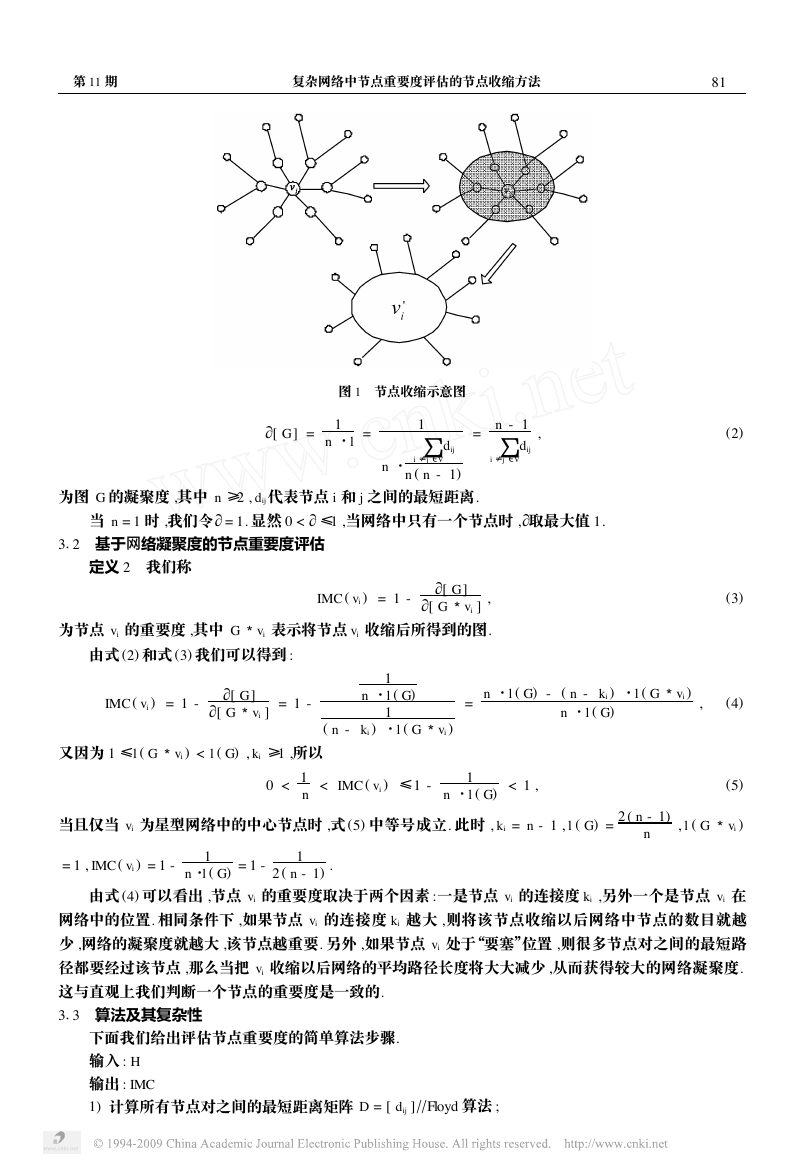3 　基于网络凝聚度的节点收缩法 3 1 　节点收缩及网络凝聚度 假设 vi 是图 G = ( V , E) 中的一个节点 ,我们用 G vi 表示将节点 vi 收缩后所得到的图. 所谓将节点 vi 收缩是指将与节点 vi 相连接的 ki 个节点都与节点 vi 融合 ,即用一个新节点代替这 ki + 1 个节点 ,原先 与它们关联的边现在都与新节点关联 ,如图 1 所示. 直观上可以这样理解节点的收缩 :我们把与节点 vi 相连接的 ki 个节点通过收缩都与节点 vi 融合 ,这 相当于节点 vi 将它周围的 ki 个节点“凝聚成了一个节点”. 如果节点 vi 是一个很重要的“核心节点”,那么 将它收缩后整个网络将更好的凝聚在一起. 最典型的例子就是如果我们将星形网中的中心节点收缩 ,整个 网络就收缩成了一个节点 ,而将其它节点收缩整个网络的凝聚程度不会发生太大的改变. 所以我们可以认 为收缩后使得网络凝聚程度越高的节点就越重要. 下面我们来定义网络的凝聚程度. 网络的凝聚程度首先取决于网络中各个节点之间的连通能力 ,我们用节点之间的平均路径长度 l 来 衡量 ,即所有节点对之间最短距离的算术平均值. 其次 ,网络的凝聚程度还取决于网络中节点数目 n. 例如 在一个社会关系网里 ,人员之间联系越方便 ( l 越小) 、人数越少 ( n 越小) ,整个网络的凝聚程度就越高. 我 们将网络的凝聚度定义为节点数 n 与平均路径长度 l 乘积的倒数. 定义 1 　我们称
    1 第 11 期 ΠΠ 复杂网络中节点重要度评估的节点收缩方法 图 1 　节点收缩示意图 　 [ G] = 1 n ·l = 1 ∑ dij n · i ≠j ∈V n ( n - 1) = n - 1 ∑ dij i ≠j ∈V , 为图 G 的凝聚度 ,其中 n ≥2 , dij代表节点 i 和 j 之间的最短距离. 当 n = 1 时 ,我们令 = 1. 显然 0 < ≤1 ,当网络中只有一个节点时 , 取最大值 1. 3 2 　基于网络凝聚度的节点重要度评估 定义 2 　我们称 为节点 vi 的重要度 ,其中 G vi 表示将节点 vi 收缩后所得到的图. IMC ( vi ) = 1 - [ G] [ G vi ] , 18 (2) (3) 由式 (2) 和式 (3) 我们可以得到 : IMC ( vi ) = 1 - [ G] [ G vi ] = 1 - 1 n ·l ( G) 1 ( n - ki ) ·l ( G = vi ) n ·l ( G) - ( n - ki ) ·l ( G n ·l ( G) vi ) , (4) 又因为 1 ≤l ( G vi ) < l ( G) , ki ≥1 ,所以 0 < 1 n < IMC ( vi ) ≤1 - 1 n ·l ( G) < 1 , 当且仅当 vi 为星型网络中的中心节点时 ,式 (5) 中等号成立. 此时 , ki = n - 1 , l ( G) = (5) 2 ( n - 1) n , l ( G vi ) = 1 , IMC ( vi ) = 1 - 1 n·l ( G) = 1 - 1 2 ( n - 1) . 由式 (4) 可以看出 ,节点 vi 的重要度取决于两个因素 :一是节点 vi 的连接度 ki ,另外一个是节点 vi 在 网络中的位置. 相同条件下 ,如果节点 vi 的连接度 ki 越大 ,则将该节点收缩以后网络中节点的数目就越 少 ,网络的凝聚度就越大 ,该节点越重要. 另外 ,如果节点 vi 处于“要塞”位置 ,则很多节点对之间的最短路 径都要经过该节点 ,那么当把 vi 收缩以后网络的平均路径长度将大大减少 ,从而获得较大的网络凝聚度. 这与直观上我们判断一个节点的重要度是一致的. 3 3 　算法及其复杂性 下面我们给出评估节点重要度的简单算法步骤. 输入 : H 输出 : IMC 1) 计算所有节点对之间的最短距离矩阵 D = [ dij ] Floyd 算法 ;
    28 系统工程理论与实践 2006 年 11 月 ] ; st [ G [ G] ; 主循环 ,评估所有节点重要度 ; 2) 根据 (2) 式计算网络初始凝聚度 3) FOR i = 1 to n {计算节点 vi 收缩后所有节点对之间的最短距离矩阵 D ( i) = [ d ( i) 　根据 (2) 式计算节点 vi 收缩后网络的凝聚度 　根据 (3) 式计算 IMC ( vi ) ; } 从上述算法步骤可以看出 ,整个算法的时间复杂性取决于节点 vi 收缩后所有节点对之间最短距离矩 阵 D = [ dij ]的计算. 因为 Floyd 算法的时间复杂性为 O ( n3 ) ,所以如果我们在每次节点收缩操作以后重新 用 Floyd 算法计算 D ( i) ,整个算法的时间复杂性将为 O ( n4 ) . 下面我们将给出一个计算 D ( i) 的时间复杂性 为 O ( n2 ) 的新算法 ,该算法只需在初始最短距离矩阵 D 基础上作少量计算即可得到 D ( i) . 这样整个评估 算法的时间复杂性将下降为 O ( n3 ) ,运算量也随之大大减少. vi ] ; 由 G 的邻接矩阵 H = [ hij ]可以得到 G 的直接距离矩阵 C = [ cij ] n ×n cij = 0 i = j i ≠ j 且 hij = 1 1 ∞ i ≠ j 且 hij = 0 , (6) 令 I = { vk ∈V| cki ≠∞}表示节点 vi 的所有相邻节点及其自身集合 ,则节点 vi 收缩相当于令 cst = 0 ,其中 s , t ∈I ,此时网络中任意节点对 ( vp , vq) ∈V ×V 之间最短距离 d′pq相对于 dpq的变化规律如下 : 1) vp ≠vi 且 vq ≠vi ①dpi + diq = dpq ,即节点 vi 处于 vp , vq 之间的最短路径上 ,则 d′pq = dpq - 2 ; ②dpi + diq = dpq + 1 ,即节点 vi 处于 vp , vq 之间的次优路径上 ,则 d′pq = dpq - 1 ; ③dpi + diq ≥dpq + 2 ,则 d′pq = dpq ; 2) vp , vq 有且仅有一个为 vi ,则 d′pq = dpq - 1 ; 3) vp = vq = vi ,则 d′pq = dpq = 0. 节点 vi 收缩以后 I 中所有节点都被新节点 v′i 代替 ,节点数目变为 n - ki ,此时只需将[ d′pq ]中与 vi ] . 在这个计算 D ( i) 的算法中 ,由于 G 是一个无向图 ,所以 2 个节点对之间的最短距离 ,从而该算法的时间复杂性为 O ( n2 ) ,整个评估算 st 相邻节点对应的行和列删去即得到 D ( i) = [ d ( i) 我们只需要计算 n ( n - 1) 法的时间复杂性为 O ( n3 ) . 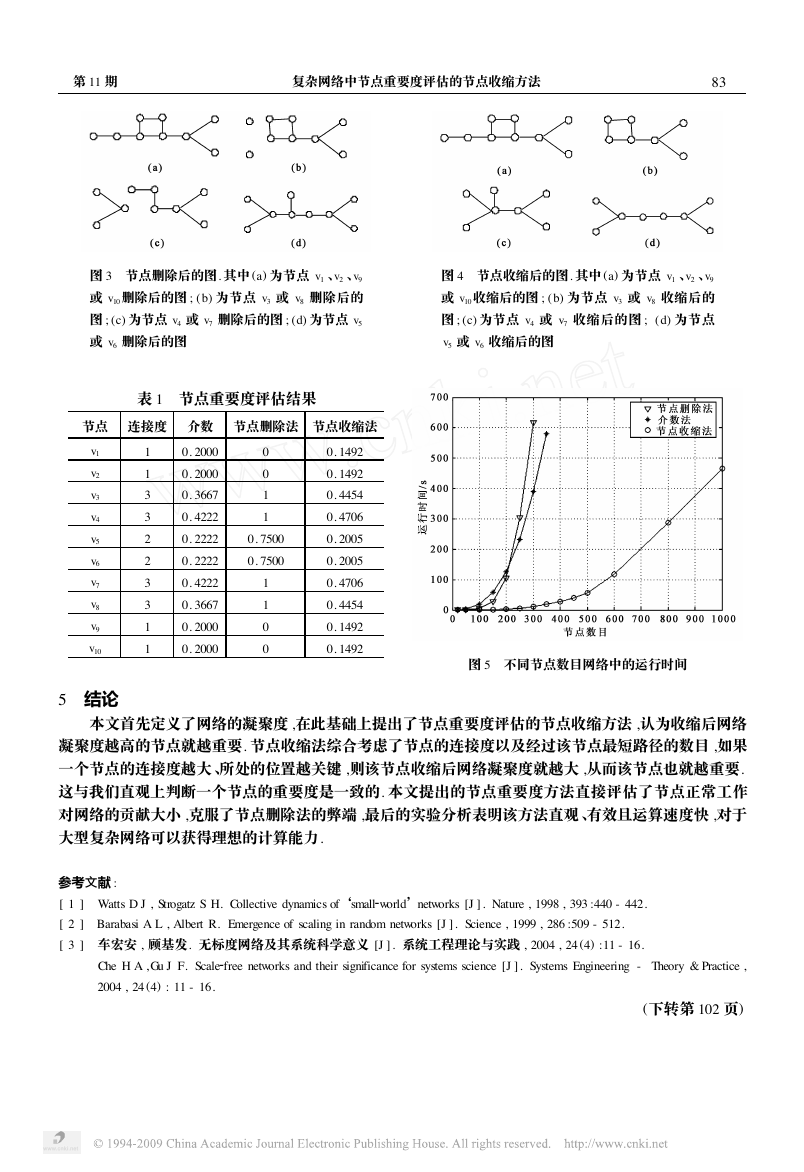4 　实验分析 如图 2 所示 ,网络中有 10 个节点 ,10 条边. 显然节点的连接度不能很好的衡量节点的重要度 ,节点 v3 、v4 、v7 、v8 的连接度都为 3 ,但它们的重要度显然不同. 分别采用文献 [ 15 ]中方法和本文方法作节点删 除 、节点收缩操作 ,结果分别如图 3 、图 4 所示. 从图 3 可以看出 v3 、v4 、v7 、v8 的删除都使得网络不再连通 , 即这些节点删除后生成树数目都为 0 ,从而重要度都为 1. 但从直观上判断 , v3 、v8 与 v4 、v7 的重要度是有 差异的. 本文方法则避免了这种情况的发生 ,区分了 v3 、v8 与 v4 、v7 的重要度. 本文方法与介数法的排序 结果是一致的 ,即 v4 , v7 →v3 , v8 →v5 , v6 →v1 , v2 , v9 , v10 . 具体评估结果如表 1 所示. 分别用本文方法 、文献[15 ]中的节点删除法和介数法在 Pentium4 2 4G Hz 微机上运行 Matlab 程序对不 同节点数目的随机网络 ( ER 模型[16 ] ,连接概率 P = 0 3) 进行重要 度评估 ,运行时间 (多次取样平均值) 如图 5 所示. 从图 5 可以看 出 ,当节点数目较多时 ,本文方法要明显快于其他两种方法 ,评估 100 个节点的重要度不超过 1 秒 ,评估 1000 个节点的重要度也不 超过 10 分钟. 这说明本文提出节点重要度评估方法是有效的 ,对 于大型复杂网络可以获得理想的计算能力. 图 2 　某网络拓扑结构图
    2 复杂网络中节点重要度评估的节点收缩方法 38 2 第 11 期 图 3 　节点删除后的图. 其中 (a) 为节点 v1 、v2 、v9 或 v10删除后的图 ; (b) 为节点 v3 或 v8 删除后的 图 ; (c) 为节点 v4 或 v7 删除后的图 ; (d) 为节点 v5 或 v6 删除后的图 图 4 　节点收缩后的图. 其中 (a) 为节点 v1 、v2 、v9 或 v10收缩后的图 ; (b) 为节点 v3 或 v8 收缩后的 图 ; (c) 为节点 v4 或 v7 收缩后的图 ; (d) 为节点 v5 或 v6 收缩后的图 　 　 表 1 　节点重要度评估结果 节点 连接度 介数 节点删除法 节点收缩法 v1 v2 v3 v4 v5 v6 v7 v8 v9 v10 1 1 3 3 2 2 3 3 1 1 0. 2000 0. 2000 0. 3667 0. 4222 0. 2222 0. 2222 0. 4222 0. 3667 0. 2000 0. 2000 0 0 1 1 0. 7500 0. 7500 1 1 0 0 0. 1492 0. 1492 0. 4454 0. 4706 0. 2005 0. 2005 0. 4706 0. 4454 0. 1492 0. 1492 图 5 　不同节点数目网络中的运行时间 5 　结论 本文首先定义了网络的凝聚度 ,在此基础上提出了节点重要度评估的节点收缩方法 ,认为收缩后网络 凝聚度越高的节点就越重要. 节点收缩法综合考虑了节点的连接度以及经过该节点最短路径的数目 ,如果 一个节点的连接度越大 、所处的位置越关键 ,则该节点收缩后网络凝聚度就越大 ,从而该节点也就越重要. 这与我们直观上判断一个节点的重要度是一致的. 本文提出的节点重要度方法直接评估了节点正常工作 对网络的贡献大小 ,克服了节点删除法的弊端 ,最后的实验分析表明该方法直观 、有效且运算速度快 ,对于 大型复杂网络可以获得理想的计算能力. 参考文献 : [ 1 ] 　Watts D J , Strogatz S H. Collective dynamics of‘small [ 2 ] 　Barabasi A L , Albert R. Emergence of scaling in random networks [J ]. Science , 1999 , 286 :509 - 512. [ 3 ] 　车宏安 , 顾基发. 无标度网络及其系统科学意义 [J ]. 系统工程理论与实践 , 2004 , 24 (4) :11 - 16. world’networks [J ]. Nature , 1998 , 393 :440 - 442. Che H A ,Gu J F. Scale 2004 , 24 (4) : 11 - 16. free networks and their significance for systems science [J ]. Systems Engineering - Theory & Practice , (下转第 102 页)
    ­ Santa Fe , New Mexico , USA. [ 5 ] 　王勋 ,凌云 ,费玉莲. 基于 Web 日志和缓存数据挖掘的电子商务推荐系统[J ]. 情报学报 ,2005 ,24 (3) :324 - 328. Wang Xun ,Ling Yun , Fei Yulian. Personalization recommendation system based on web log & cache data mining[J ]. Journal of the China Society for Scientific and Technical Information ,2005 ,24 (3) :324 - 328. [ 6 ] 　Fu X ,Budazik J , Hammond K J . Mining navigation history for recommendation[ C] Proc of the International Conf on Intelligent 201 系统工程理论与实践 2006 年 11 月 User Interfaces , ACM. New Orleans. LA , ACM , 2000 :106 - 112. [ 7 ] 　Qiubang Li , Rajiv Khosla. An adaptive algorithm for improving recommendation quality of E recommendation systems [ C ] CIMS2003 , Switzerland , 29 - 31 ,July 2003 :109 - 203. International Symposium on Computational Intelligence for Measurement Systems and Applications. Lugano , [ 8 ] 　高琳琦 ,李龙洙. 基于顾客行为的产品推荐方法[J ]. 计算机工程与应用 ,2005 (3) :188 - 190. Gao Linqi ,Li longzhu. Production recommender method based on customer’s behavior[J ]. Computer Engineeting and Applications , 2005 (3) :188 - 190. [ 9 ] 　梁邦勇 , 李涓子 , 王克宏. 基于语义 Web 的网页推荐模型 [J ]. 清华大学学报 (自然科学版) ,2004 ,44 (9) :1272 - 1276. Liang Bangyong , Li Juanzi , Wang Kehong. Web page recommendation model for the semantic web [J ]. Journal of Tsinghua University (Science & Technology) , 2004 ,44 (9) :1272 - 1276. [10 ] 　崔林 ,宋瀚涛 , 陆玉昌. 基于语义相似性的资源协同过滤技术研究[J ]. 北京理工大学学报 ,2005 , 25 (5) : 402 - 405. Cui Lin , Song Hantao , Lu Yuchang. A study on item Transactions of Beijing Institute of Technology , 2005 , 25 (5) : 402 - 405. based collaborative filtering algorithm using semantic similarity [ J ]. [ 11 ] 　Robin Burke. Semantic ratings and heuristic similarity for collaborative filtering[DB OL ]. 2000 ,http : www. igec. umbc. edu kbem final burke. pdf. [12 ] 　Budanitsky , Alexander , Hirst , Graeme. Evaluating wordNet based measures of semantic distance [J ]. Computational Linguistics , 2006 ,32 (1) :13 - 47. [13 ] 　Yuhua Li , Zuhair A. Bandar , David McLean. An approach for measuring semantic similarity between words using multiple information sources[J ]. IEEE Transactions on Knowledge and Data Engineering ,2003 ,15 (4) . [14 ] 　Matthew Garden and Gregory Dudek. Semantic feedback for hybrid recommendations in Recommendz [ DB OL ]. http : www. citeulike. org user bj article 380924. (上接第 83 页) [ 4 ] 　方锦清 , 汪小帆 , 刘曾荣. 略论复杂性问题和非线性复杂网络系统的研究 [J ]. 科技导报 , 2004 , (2) : 9 - 12 ,64. Fang J Q , Wang X F , Liu Z R. On the study of complexity and nonlinear complex networks [J ]. Science & Technology Review , 2004 , (2) : 9 - 12 , 64. [ 5 ] 　Callaway D S , Newman M E J , Strogatez S H , et al. Network robustness and fragility : Percolation on random graphs [J ]. Phys Rev Lett , 2000 , 85 (25) : 5468 - 5471. [ 6 ] 　Albert R , Jeong H , Barabási A [ 7 ] 　Gallos L K, Cohen R , Argyrakis P. Stability and topology of scale L. Error and attack tolerance of complex networks [J ]. Nature , 2000 , 406 : 378 - 382. free networks under attack and defense strategies [J ]. Phys Rev Lett , 2005 , 94 : 188701. [ 8 ] 　Ball M O , Golden B L , Vohra R V. Finding the most vital arcs in a network [J ]. Oper Res Lett , 1989 , 8 : 73 - 76. [ 9 ] 　Page L B , Perry J E. Reliability polynomials and link importance in networks [J ]. IEEE Tans Reliability , 1994 , 43 (1) : 51 - 58. [10 ] 　Hsu L H , Jan R H , Lee Y C , et al. Finding the most vital edge with respect to minimum spanning tree in weighted graphs [J ]. Info Proc Lett , 1991 , 39 : 277 - 281. [11 ] 　Freeman L C. A set of measures of centrality based upon betweenness [J ]. Sociometry , 1977 , 40 : 35 - 41. [12 ] 　Wasserman S , Faust K. Social Network Analysis : Methods and Applications[M]. Cambridge : Cambridge University Press , 1994. [13 ] 　Corley H W , Sha D Y. Most vital links and nodes in weighted networks [J ]. Oper Res Lett , 1982 , 1 : 157 - 160. [14 ] 　Nardelli E , Proietti G, Widmayer P. Finding the most vital node of a shortest path [J ]. Theoretical Computer Science , 2001 , 296 (1) : 167 - 177. [15 ] 　陈勇 , 胡爱群 , 胡骏 ,等. 通信网中最重要节点的确定方法[J ]. 高技术通讯 , 2004 , 1 : 573 - 575. Chen Y, Hu A Q , Hu J , et al. A method for finding the most vital node in communication networks [J ]. High Technol Lett , 2004 , 1 : 573 - 575. [16 ] 　Erd s P , Rényi A. On random graphs [J ]. Publ Math , 1959 , 6 : 290 - 297.
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料