灵敏度过滤技术在拓扑优化中的应用研究 http://www.paper.edu.cn 赵丹宁 1，丁繁繁 2 1 河海大学工程力学系，江苏南京（210098） 2 苏州二建集团钢结构分公司，江苏苏州 (215000) E-mail：zdn19811981@163.com 摘 要：棋盘格现象是结构拓扑优化中的普遍现象。本文介绍了连续体结构拓扑优化中的棋 盘格现象以及产生原因，并对目前解决这一问题的各种方法进行了分析研究。本文借鉴灵敏 度再分配抑制棋盘格的过滤方法，给出基于一阶灵敏度再分配的算法流程及程序框图，编制 相应的计算机程序，减弱结构拓扑优化中的棋盘格现象，并通过算例进行比较分析，证明此 方法的可行性。 关键词：棋盘格，拓扑优化，灵敏度过滤技术，连续体 1. 引 言 结构拓扑是当前结构优化领域内最具有挑战性的课题之一，也是当前结构优化设计领域 的研究热点。由于其难度大，连续体结构拓扑优化理论的研究直到近十多年才取得飞速发展。 结构拓扑优化主要是指在特定的设计区域内，满足给定的约束条件，寻求目标函数最小或最 大的最优的材料分布形式，从而确定结构中空洞的数量、位置及其连接形式[1][2]。 棋盘格式是连续体结构拓扑优化中常见的一种现象。对于棋盘格产生的原因，目前尚没 有本质上的定论。在拓扑优化中，棋盘格式的出现与所采用的材质设计变量无关，即不论是 采用均匀化设计方法还是采用密度法，均会出现棋盘格式。在早期结构拓扑优化研究中，有 些学者误人为这事一种较为较优的理想的结构。但从生产角度来讲，不但加工困难，成本也 很高，不符合实际应用。从材料本身讲，也不符合材料的最优分布原则，棋盘格使结构形状 的提取和制造变得困难，因为设计者必须在元素与孔洞之间作取舍。因而这并不是我们需要 的最优解。 近代一些学者针对此现象提出了自己的看法，Jog 和 Haber 认为是密度变量和唯一变量 的混合变分问题，并证明在特定的组合下是可以避免棋盘格的出现，其中 Haber 提出的周长 约束法，此法是通过限制结构的周长来抑制棋盘格式的出现但周长的约束值事先难以确定， 只能通过试验方法得到，给实际应用带来困难[3][4]；Kikuchi 认为棋盘格式的出现是由于相邻 单元间设计变量值变化过大引起的，基于此理论 Kikuchi 提出了一种超级单元法，但这种方 法并不能彻底消除棋盘格式[5]。 解决棋盘格式最简单的方法是采用高阶有限单元代替低阶有限单元，增加单元自由度， 如采用多节点单元。但在单元数目相同的情况下，分析高节点单元结构的时间要比分析低节 点单元结构的长得多，尤其在三维结构上更加明显。 上述这些方法都能不同程度的解决棋盘格现象，但是不能完全解决，而是在某些程度上 减弱了棋盘格现象。本文中使用的方法是参考 Li、Qing 和 Steven 等人在二维结构上减弱棋 盘格单元的应用[6]。该方法是在拓扑优化过程中对作为材料删除判据的灵敏度进行再分配 （如本文作为材料删除判据的灵敏度就为单元应力），有效地改善由于数值不稳定造成的灵 敏度在单元之间的高低分布现象，抑制材料删除后的拓扑构形中出现孔洞单元和实体单元呈 周期性分布，从而有效地抑制棋盘格式，此方法同样适用于三维结构。 - 1 - 

http://www.paper.edu.cn 2. 灵敏度再分配的抑制法及其计算原理 2.1 二维结构单元权重的一阶再分配计算原理 灵敏度再分配抑制棋盘格单元的方法是重新计算每个单元的应力值，使得当邻近单元 应力值较高或较低时，此单元的应力值也会随之提高或减少。 这种方法首先按式(1)计算连接到第 k 个节点的单元应力平均值 kα , α k ne i ∑ V α i i 1 == ne ∑ V i i 1 = (1) 式中， n 为第e 个元素周围的节点数目； ne 为连接到第 k 个节点的元素个数； iα 为第i 个元素的等效应力； iV 为第i 个元素的体积 然后再重新式按(2)计算第e 个元素周围节点应力的平均值 eα α e = 1 n ∑ n 1 i = α k (2) 将式(1)代入式(2)，可得到第 e 个元素的应力如式(3)所示： α e m ∑ i 1 == m ∑ i 1 = αω i V i i V ω i i 式中， m 为单元e 周围所有单元的总数； iω为单元e 周围第i 个单元的权重 (3) 其权重应满足式(4) m =∑ 1 i 1 = iω (4) 2.2 二维结构单元权重的一阶再分配格式 采用有限元计算 4 节点单元，根据上述算式，计算出 4 节点单元的权重。 在二维平面 连续体结构中，权重按单元位置的不同可分为 3 类，分别是位于连续体区域上的角点单元、 边界单元和一般性单元。具体数值参照图 1。 - 2 - 

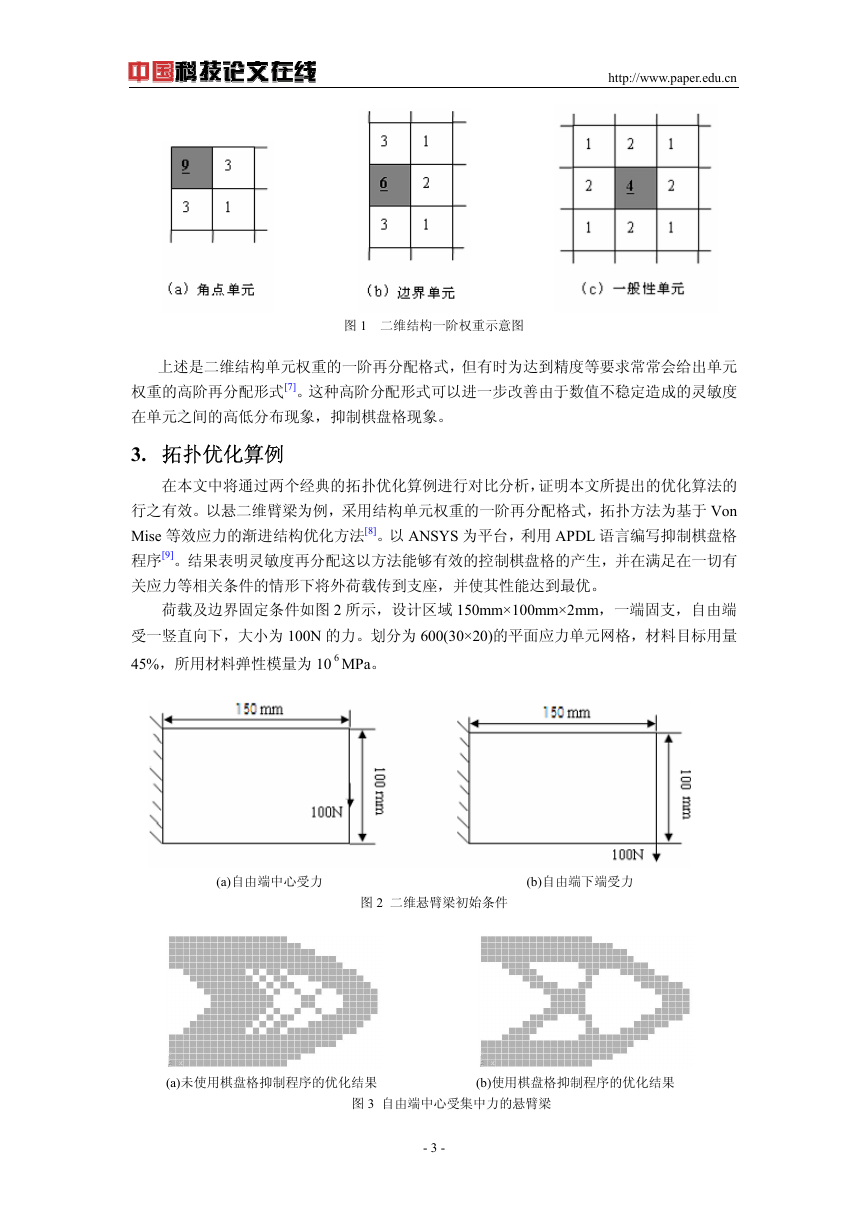
http://www.paper.edu.cn 图 1 二维结构一阶权重示意图 上述是二维结构单元权重的一阶再分配格式，但有时为达到精度等要求常常会给出单元 权重的高阶再分配形式[7]。这种高阶分配形式可以进一步改善由于数值不稳定造成的灵敏度 在单元之间的高低分布现象，抑制棋盘格现象。 3. 拓扑优化算例 在本文中将通过两个经典的拓扑优化算例进行对比分析，证明本文所提出的优化算法的 行之有效。以悬二维臂梁为例，采用结构单元权重的一阶再分配格式，拓扑方法为基于 Von Mise 等效应力的渐进结构优化方法[8]。以 ANSYS 为平台，利用 APDL 语言编写抑制棋盘格 程序[9]。结果表明灵敏度再分配这以方法能够有效的控制棋盘格的产生，并在满足在一切有 关应力等相关条件的情形下将外荷载传到支座，并使其性能达到最优。 荷载及边界固定条件如图 2 所示，设计区域 150mm×100mm×2mm，一端固支，自由端 受一竖直向下，大小为 100N 的力。划分为 600(30×20)的平面应力单元网格，材料目标用量 45%，所用材料弹性模量为 10 6 MPa。 (a)自由端中心受力 (b)自由端下端受力 图 2 二维悬臂梁初始条件 (a)未使用棋盘格抑制程序的优化结果 (b)使用棋盘格抑制程序的优化结果 图 3 自由端中心受集中力的悬臂梁 - 3 - 

http://www.paper.edu.cn (a) 未使用棋盘格抑制程序的优化结果 (b) 使用棋盘格抑制程序的优化结果 图 4 自由端下端受集中力的悬臂梁 对比两组采用抑制技术前后的拓扑优化结果，未使用棋盘格抑制技术的拓扑结果中存 在大量的棋盘格格式，如图 3、4 中的（a），图形复杂，计算不稳定，导致程序计算被迫停 止。而使用了一阶棋盘格抑制技术的优化过程明显消除了棋盘格现象，如图 3、4 中的（b）， 并且出现了非常清晰的拓扑形式。 表 1 剩余体积率对照比较表 自由端中心受载 自由端下端受载 单元应力再分配前剩余体积率（%） 单元应力再分配前剩余体积率（%） 68 45 67 44 表 2 同删除率下再分配后的最大等效应力对照比较表（以自由端中心受载为例） 删除率（%） 3 5 8 单元应力再分配前最大等效应力值（E*4） 1.5 1.5 1.5 单元应力再分配后最大等效应力值（E*4） 1 1 1 10 1.5 1 13 1.5 1 15 1.5 1 18 20 22 1.5 1.6 2 1.1 1.4 1.8 24 2.3 2 由表 1 可以看出，使用抑制技术的二维悬臂梁与未使用抑制技术的相比。优化结果不但 满足体积率的目标要求，而且图形简单。 由表 2 可以明显看出，再分配后单元最大等效应力值的明显小于分配前的。同等删除条 件下，最大等效应力值变小会导致每次迭代删除的单元数会变少，这样会导致迭代步骤增多， 计算量增加。 结构内部的应力、应变本是连续的，而有限元技术中，由于人为的划分网格使原本有无 数点相连的结构变成只有有限个点来维系，内部相邻区域中的单元灵敏值也变得不连续。一 阶再分配技术均化了相邻单元的灵敏度，缓和了人为对结构优化造成的误差，计算结果更符 合实际情况，更为合理有效。 4. 结论 本文给出了使用抑制棋盘格的一阶灵敏度再分配使用方法的实例。证明了灵敏度再分配 法的有效与实用性，本文在此只采用了基于应力准则的灵敏度再分配法，除此之外还可以采 用应变、位移等使用准则，也可以将这些准则糅合运用。这些拓扑优化方法有待继续研究。 - 4 - 

http://www.paper.edu.cn 参考文献 [1] 程耿东.结构优化新方法及其计算机实现[J].力学与实践，1992, 14(1): 1~6. [2] Bendsoe M .P .Kikuchi N .Generating optimal topologies inoptimal design using a homogenization method [J].Comp meth Appl Mech Engng 1988,71:197~224. [3] Jog C. S. Harber R. B. Sability of finite element models for distributed-parameter optimization and topology design [J]. Comp Meth Appl Mech Engrg,1996,130:203~226. [4] Harber R. B. Jog C. S. Bendsoe M. P. A new approach to variable topology, shape design using a constraint on perimeter [J]. Struct Optim,1996,11:1~12. [5] Bendsoe M. P. Kikuchi N. Generating Optimal Topologie in Structural Design Usinga Homogenization Method [J]. Comp Meth Appl Mech Engrg,1988,71(1):197~224. [6] Li Q. Steven GP, Xie YM.A simple checkerboard suppression algorithm for evolutionary structural optimization [J]. Struct Multidisc.Optim,2001,22(13):230~239 [7] 郭中泽，陈裕泽，张卫红等.渐进优化法的一种高阶棋盘格式抑制方法[J]. 机械设计.2006，5：1~4 [8] 角镇佑. 以应力为基之迭代式拓扑设计方法[D]. 台湾科技大学，2006. [9] 博弈工作室. APDL 参数化有限元分析技术及其应用实例[M]. 中国水利水电出版社,2004,第一版 The application of filtration technique of sensitivity in topology optimization Zhao Danning1, Ding Fanfan2 1Hohai University, Nanjing (210098) 2 SUZHOU NO.2 CONSTRUCTION & GROUP CO.LTD, Suzhou (215000) Abstract The checker-board pattern is one universally phenomena in the topology optimization of structures. The checker-board pattern and its causation in the topology optimization of continuum structures has been summarized in this paper. It introduce and analyse some exiting theoretical issues to this problem. Based on the filtration technique of sensitivity redistribution to restrain the checker-board pattern, applying the Ansys software platform, the numerical procedures has been developed.The feasibility of the method has been analysed and demonstrated by the result. Keywords: checker-board pattern, topology optimization, the filtration technique of sensitivity, continuum structures - 5 -