使用标号算法(Ford-Fulkerson)解决最大流问题。.doc

发布时间：2022-05-30 发布人：admin 分类：说明书资料大小：0.06M 资料格式：doc 举报版权申诉

l316236540-1666152-16359647621957934388.doc.pdf-第1页.png

第1页 / 共6页

l316236540-1666152-16359647621957934388.doc.pdf-第2页.png

第2页 / 共6页

l316236540-1666152-16359647621957934388.doc.pdf-第3页.png

第3页 / 共6页

l316236540-1666152-16359647621957934388.doc.pdf-第4页.png

第4页 / 共6页

l316236540-1666152-16359647621957934388.doc.pdf-第5页.png

第5页 / 共6页

l316236540-1666152-16359647621957934388.doc.pdf-第6页.png

第6页 / 共6页

文本预览

云南大学数学系《运筹学通论》课程上机实验报告课程名称：运筹学任课教师：李建平上机实验名称：标号算法解决最大流问题上机实验编号：4 一．实验目的上机实验成绩：年级：2006 姓名：马力学号：20061910164 上机实验日期：专业：信计国防生组号：007 2009.6.16 上机实验时间：第 17 周使用标号算法(Ford-Fulkerson)解决最大流问题。其基本思想是从某个可行流 F 出发，找到关于这个流的一个可改进路经 P，然后沿着 P 调整 F，对新的可行流试图寻找关于他的可改进路经，如此反复直至求得最大流。二．实验内容 1.标号过程在这个过程中,网络中的点或者是标号点(又分为已检查和未检查两种),或者是未标号点,每个标号点的标号包含两部分:第一个标号表明它的标号是从哪一点得到的,以便找出增广链;第二个标号是为确定增广链的调整量用的. 标号过程开始,总先給 Vs 标上(0, +  ),这时 Vs 是标号而未检查过的点,其余都是未标号的点.一般地,取一个标号而未检查的点 Vi, 对一切未标号的点 Vj: (1).若在弧( Vi, Vj)上,Fij0, 则給 Vj 标号(-Vi,l(Vj)),这里 l(Vj)=min[l(Vi),Fij].这时点 Vj 成为标号而未检查的点.若所有标号都是已检查过的,而标号过程进行不下去时,则算法结束,这时的可行流就是最大流. 2.调整过程首先按 Vt 及其他点的第一个标号,利用”反向追踪”的办法,找出增广链 u. 例如设 Vt 的第一个标号为 Vk(-Vk) , 则弧(Vk,Vt)(Vt,Vk)是 u 上的弧. 接下来检查 Vk 的第一个标号,若为 Vi (-Vi) , 则找出(Vi,Vk)(或相应的(Vk,Vi)).再检查的第一个标号,依此下去,直到为止.这时被找出的弧就构成了增广链 u. 令调整量θ是 l(Vt),即 Vt 的第二个标号: Fij﹢θ （vi，vj）∈u+ Fij﹣θ （vi，vj）∈u- Fij=      Fij （vi，vj）u 去掉所有的标号,对新的可行流 F’={Fij ‘},重新进入标号过程. 三．使用环境

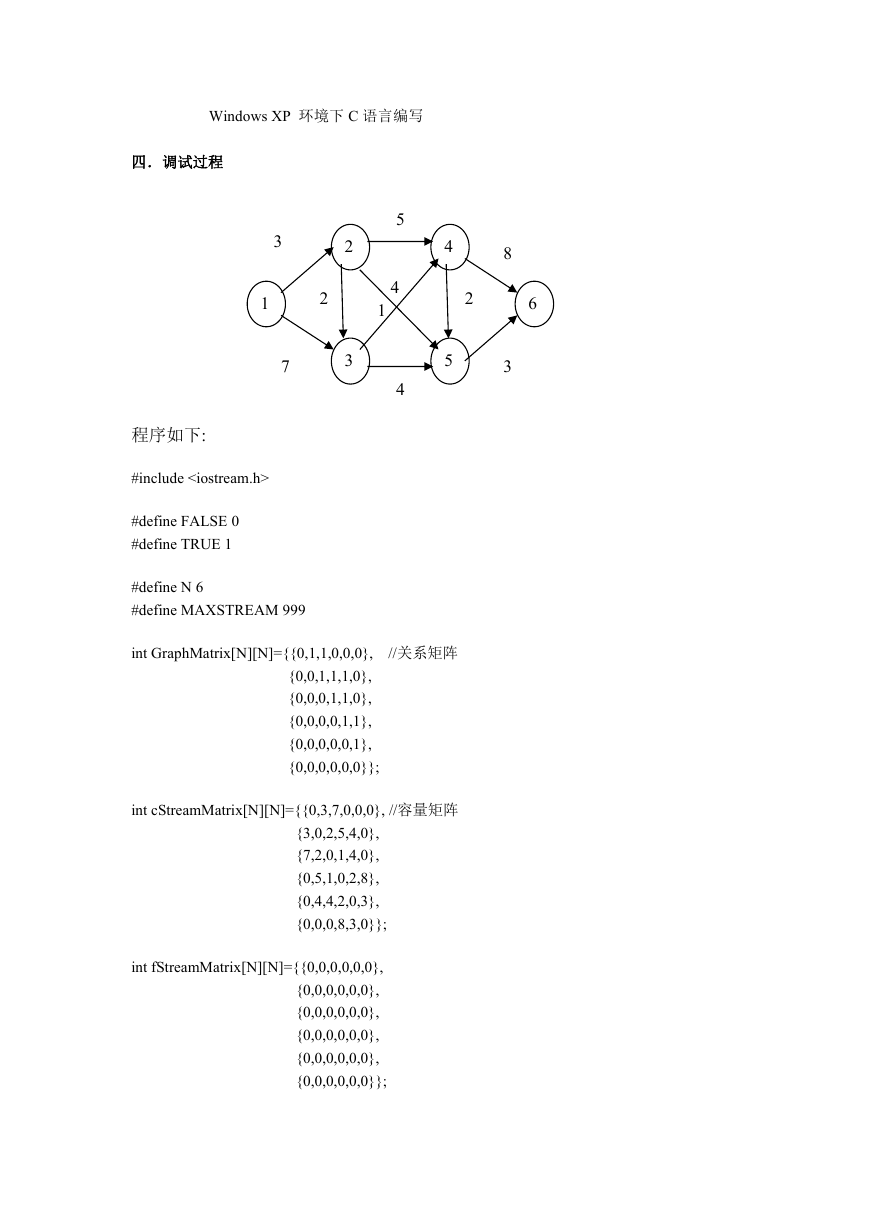
Windows XP 环境下 C 语言编写四．调试过程 3 1 1 7 2 2 3 1 3 5 4 1 4 2 4 5 6 8 3 程序如下: #include #define FALSE 0 #define TRUE 1 #define N 6 #define MAXSTREAM 999 //关系矩阵 int GraphMatrix[N][N]={{0,1,1,0,0,0}, {0,0,1,1,1,0}, {0,0,0,1,1,0}, {0,0,0,0,1,1}, {0,0,0,0,0,1}, {0,0,0,0,0,0}}; int cStreamMatrix[N][N]={{0,3,7,0,0,0}, //容量矩阵 {3,0,2,5,4,0}, {7,2,0,1,4,0}, {0,5,1,0,2,8}, {0,4,4,2,0,3}, {0,0,0,8,3,0}}; int fStreamMatrix[N][N]={{0,0,0,0,0,0}, {0,0,0,0,0,0}, {0,0,0,0,0,0}, {0,0,0,0,0,0}, {0,0,0,0,0,0}, {0,0,0,0,0,0}};

struct NetNodeType { int Flag; int cStream; int fStream; }NetMatrix[N+1][N+1]; struct NodeType { int Label; int Stream; }Node[N+1]; void Initialize(void)//初始化 { int i,j; for (i=1;i<=N;i++) { for (j=1;j<=N;j++) { NetMatrix[i][j].Flag=GraphMatrix[i-1][j-1]; NetMatrix[i][j].cStream=cStreamMatrix[i-1][j-1]; NetMatrix[i][j].fStream=fStreamMatrix[i-1][j-1]; } Node[i].Label=Node[i].Stream=0; } } int Find_Maximum_Stream(void) { int z; int c,f,x,y,i,u,v; int Max_Stream_Found,dStream; dStream=MAXSTREAM; //标号过程 Node[1].Label=1; Node[1].Stream=MAXSTREAM; for (x=1;x<=N;x++) if (Node[x].Label!=0) for (y=1;y<=N;y++) if (NetMatrix[x][y].Flag==1 && Node[y].Label==0) { c=NetMatrix[x][y].cStream; f=NetMatrix[x][y].fStream; if (f

} else if (NetMatrix[y][x].Flag==1 && Node[y].Label==0) { f=NetMatrix[y][x].fStream; if (f>0) { Node[y].Label=-x; Node[y].Stream=((f0) NetMatrix[v][u].fStream=NetMatrix[v][u].fStream+dStream; else if (v<0) { v=-v; NetMatrix[u][v].fStream=NetMatrix[u][v].fStream-dStream; } u=v; }while (v!=1); for (i=1;i<=N+1;i++) { Node[i].Label=0; Node[i].Stream=0; } Max_Stream_Found=FALSE; } else Max_Stream_Found=TRUE; z=Max_Stream_Found; return(z); } void Output_Stream(void) { int MaxStream=0; int i,j; for (i=1;i<=N;i++) if (NetMatrix[1][i].Flag==1) MaxStream+=NetMatrix[1][i].fStream;

cout<<"Maximum Stream="<

六．实验总结 1.求最大流的方法中除了标号算法(Ford-Fulkerson)外,还有一个很有效的算法就是 Edmonds-Karp 算法: 若给定一个可行流 F=(Fij)，我们把网络中使 Fij=Cij 的弧称为饱和弧，Fij><<数据结构>><<离散数学>>这三本书中知识点完成的,由于 Edmonds-Karp 算法和圈算法自己不太会,所以在找最大流时就用了标号算法 (Ford-Fulkerson),这个算法的特点就是有两步: 一个标号过程,一个调整过程.在实际操作中我们要仔细体会正向弧和反向弧时对点的标号,这样在调整过程中才能使结果正确. 3.之前由于没有看太多书,自己忽略了很多情况.例如: 若在弧( Vj, Vi)上,Fij>0, 则給 Vj 标号(-Vi,l(Vj)),这里 l(Vj)=min[l(Vi),Fij].这时点 Vj 成为标号而未检查的点.这种情况没有在程序中实现.后来看了书加上这种情况. 4.加强理论学习和上机实践，感觉两方面自己都做的不好，望今后能做的更好些. 5.在实验中出现了很多错误，例如对 C++不熟悉，在进行编译就出错。

分享到：

赞收藏

资料库

使用标号算法(Ford-Fulkerson)解决最大流问题。.doc

相关推荐

开发技术

热门标签

最新资料