新型PID控制及其应用(共六讲).pdf

发布时间：2022-06-09 发布人：admin 分类：说明书资料大小：1.16M 资料格式：pdf 举报版权申诉

johnsonxjq-11615313-16359647507532816685.pdf-第1页.png

第1页 / 共31页

johnsonxjq-11615313-16359647507532816685.pdf-第2页.png

第2页 / 共31页

johnsonxjq-11615313-16359647507532816685.pdf-第3页.png

第3页 / 共31页

johnsonxjq-11615313-16359647507532816685.pdf-第4页.png

第4页 / 共31页

johnsonxjq-11615313-16359647507532816685.pdf-第5页.png

第5页 / 共31页

johnsonxjq-11615313-16359647507532816685.pdf-第6页.png

第6页 / 共31页

johnsonxjq-11615313-16359647507532816685.pdf-第7页.png

第7页 / 共31页

johnsonxjq-11615313-16359647507532816685.pdf-第8页.png

第8页 / 共31页

第一讲_PID控制原理和自整定策略

第二讲_自适应PID控制

第三讲_智能PID控制

第四讲_模糊PID控制

第五讲_多变量PID控制器

第六讲新型PID控制器及其发展

·06· 工业仪表与自动化装置　　　　　　　　　　　　1997 年第 4 期新型 P ID 控制及其应用第一讲　P ID 控制原理和自整定策略陶永华华东冶金学院　马鞍山: 243002 　　编者按　随着控制仪表的发展, 新的控制技术不断出现, 先进的控制算法不断产生和发展。本刊以前曾发表不少这类的专题文章。为了使读者能系统了解这个领域的内容和产品发展概况, 我们特请陶永华教授以讲座形式作全面介绍。讲座共分六讲: 第一讲, P ID 控制原理和自整定策略; 第二讲, 自适应 P ID 控制; 第三讲, 智能 P ID 控制; 第四讲, 模糊 P ID 控制; 第五讲, 多变量 P ID 控制; 第六讲, 新型控制器产品发展概述。　　P ID 控制是最早发展起来的控制策略之一, 由于其算法简单、鲁棒性好、可靠性高等优点, 被广泛应用于工业过程控制。当用计算机实现后, 数字 P ID 控制器更显示出参数调整灵活、算法变化多样、简单方便的优点。随着生产的发展, 对控制的要求也越来越高, 随之发展出许多以计算机为基础的新型控制算法, 如自适应 P ID 控制、模糊 P ID 控制、智能 P ID 控制等等。本讲座共分 6 讲, 将着重介绍这些新型 P ID 控制原理、方法及其应用。我们期待着把 P ID 控制提到一个新的水平。 1　P ID 控制原理 1　模拟 P ID 控制器 1 模拟 P ID 控制系统原理框图如图 1- 1 所示, 系统由模拟 P ID 控制器和受控对象组成。图 1- 1　模拟 P ID 控制系统原理框图　　P ID 控制器根据给定值 r (t) 与实际输出值 c (t) 构成的控制偏差: 　　　　e (t) = r ( t) - c ( t) (1- 1) 将偏差的比例 (P )、积分 ( I) 和微分 (D ) 通

1997 年第 4 期　　　　　　　　　　　　工业仪表与自动化装置 ·16· 过线性组合构成控制量, 对受控对象进行控制。其控制规律为: u ( t) = K p [ e ( t) + 1 T I t 0 e ( t) d t + T D ] d e ( t) d t (1- 2) 或写成传递函数形式: U (S ) E (S ) = K P (1+ G (s) = + T DS ) (1- 3) 式中, K P 为比例系数, T I 为积分时间常数, T D 为微分时间常数。 1 T IS 简单说来, P ID 控制器各校正环节的作用是这样的: ●比例环节: 即时成比例地反应控制系统的偏差信号 e ( t) , 偏差一旦产生, 控制器立即产生控制作用以减小误差。 ●积分环节: 主要用于消除静差, 提高系统的无差度, 积分作用的强弱取决于积分时间常数 T I, T I 越大, 积分作用越弱, 反之则越强。 ●微分环节: 能反应偏差信号的变化趋势 (变化速率) , 并能在偏差信号值变得太大之前, 在系统中引入一个有效的早期修正信号, 从而加快系统的动作速度, 减小调节时间。 1 2　数字 P ID 控制器当计算机实现 P ID 控制时, 首先必须将上述 P ID 控制规律的连续形式变成离散形式, 然后才能编程实现。P ID 控制器控制算法的离散形式为: u (k ) = K P {e (k ) + T T I e (k - 1) } 或 k ∑ j = 0 e ( j ) + T D T [ e (k ) - (1- 4) u (k ) = K P ·e (k ) + K I∑ e ( j ) + K D [ e (k ) k j= 0 - e (k - 1) ] 式中　T ——采样周期 (1- 5) k ——采样序号, k = 0, 1, 2, … u (k ) ——第 k 次采样时刻的计算机输出值由 Z 变换的性质: Z [ e (k - 1) = Z - 1E (Z ) Z [∑ k e ( j ) = E (Z ) 式 (1- 5) 的 Z 变换式为: j= 0 (1- Z - 1) U (Z ) = K P E (Z ) + K IE (Z ) K D [ E (Z ) - Z - 1E (Z ) ] (1- 6) 由式 (1- 6) 便可得到数字 P ID 控制器的 Z 传递函数: (1- Z - 1) + G (Z ) = U (Z ) E (Z ) = K P + K I (1- Z - 1) + K D (1- Z - 1) (1- 7) 或者 G (Z ) = K P (1- Z - 1) + K I+ K D (1- Z - 1) 2 1- Z - 1 (1- 8) 数字 P ID 控制器如图 1- 2 所示。图 1- 2　数字 P ID 控制器框图　　由于计算机输出的 u (k ) 直接去控制执行机构 (如阀门) , u (k ) 的值和执行机构的位置 (如阀门开度) 是一一对应的, 所以我们通常称式 (1 - 4) 或式 (1- 5) 为位置式控制算法。当执行机构需要的是控制量的增量 (例如去驱动步进电机) 时, 可由式 (1- 5) 导出提供增量的 P ID 控制算式。根据递推原理可得: u (k - 1) = K P ·e (k - 1) + K I∑ e ( j ) k- 1 j= 0 e (k ) ——第 k 次采样时刻输入的偏差值 + K D [ e (k - 1) - e (k - 2) ] (1- 9) K I= K D = K P T T I K P T D T ——称为积分系数 ——称为微分系数用式 (1- 5) 减式 (1- 9) 可得: u (k ) = K P [ e (k ) - e (k - 1) + K Ie (k ) + K D [ e (k ) - 2e (k - 1) + e (k - 2) ]

ΣÙ 工业仪表与自动化装置　　　　　　　　　　　　1997 年第 4 期 e (k ) - (1—10) G (S) = K P (1+ + T DS) 有 Zieg ler- N icho ls 整定公式: 1 T IS K · 2T P K P = 1 T I= 2 T D = 0 实际应用时, 通常根据阶跃响应曲线 (图 2 (2—2) 5 - 1) , 人工测量出 K、T P、参数, 然后按式 (2- 2) 计算 K P、T I、T D。用计算机进行辅助设计时, 一是可以用模式识别的方法识别出这些特证参数; 一是可用曲线拟合的方法将阶跃响应数据拟合成近似的一阶惯性加纯延迟环节的模型。图 2- 1　阶跃响应曲线 1 2 2　 IST E 最优设定方法庄敏霞与 A therton 针对各种指标函数得出了最优 P ID 参数整定的算法, 考虑下面给出的最优指标通式。 ∞ ) = J n ( (2- 3) 这里 e ( t) 为进入 P ID 控制器的误差信号。 , t) ]2d t [ tne ( 0 根据设定点信号的最优自整定算法, 对式 (2- 3) 中给出的最优指标, 着重考虑 3 种情况, 即 n = 0, 简记作 ISE ( in teg ral squared erro r) 准则; n = 1, 简记作 IST E 准则; n = 2, 简记为 IST 2E 准则。若已知系统的数学模型如式 (2- 1) 给出, 则对典型 P ID 结构可以建立经验公式: K P = a 1 K ( T P ) b1 T I= T P a 2+ b2 ( T D = a 3T P ( T P ) T P ) b3 (2- 4) Σ ·26· = K P e (k ) + K Ie (k ) + K D [ e (k - 1) ] 式中　 e (k ) = e (k ) - e (k - 1) 式 (1- 10) 称为增量式 P ID 控制算法。将上式整理, 合并后得: u (k ) = A ·e (k ) - B ·e (k - 1) + C ·e (k - 2) (1- 11) ) 式中　A = K P (1+ T T I B = K P · (1+ C = K P T D T + T D T 2T D T ) 它们都是与采样周期, 比例系数、积分时间常数、微分时间常数有关的系数。增量式 P ID 和位置式 P ID 实质是一样的, 但增量式比位置式有许多优越之处: ● u (k ) 只与 k、k - 1、k - 2 时刻的偏差有关, 节省内存和运算时间。 ●每次只作 u (k ) 计算, 而与位置式中积分项∑e ( j ) 相比, 计算误差影响小。 ●若执行机构有积分能力 (如步进电机) , u (k ) , 即执行机构的变则每次只需输出增量化部分, 误动作造成的影响小。 ●手动—自动切换时冲击小, 便于实现无扰动切换。在具体应用数字 P ID 控制器时, 可采用一些改进算法、如积分分离 P ID 控制算法、不完全微分 P ID 控制算法, 带死区的 P ID 控制、变速积分 P ID 算法等。 2　自整定 P ID 控制策略　　P ID 控制器中 3 个参数的确定问题是实际中的设计问题。下面介绍几种较成熟的自整定方法: 2 2 1　Z ieg ler- N icho ls 设定方法受控对象大多可近似用一阶惯性加纯延迟 1　经验公式法 1 环节来表示, 传递函数为: s G P (s) = K e- 对于典型 P ID 控制器: (T PS + 1) (2- 1)

Ù 对不同的 T P 范围, 可以得出 (a, b) 参数表如表 2- 1 所示。由表中给出的 P ID 参数设置可以通过M A TLAB 来简单地实现。表 2- 1　设定点 P ID 控制器参数表 T P 范围准则 a1 b1 a2 b2 a3 b3 0 1—1 1 1—2 ISE ISTE TS I2E ISE ISTE IST 2E 1 048 1 042 0 968 1 154 1 142 1 061 - 0 897 - 0 897 - 0 904 - 0 567 - 0 579 - 0 583 1 195 0 987 0 977 1 047 0 919 0 892 - 0 368 - 0 238 - 0 253 - 0 220 - 0 172 - 0 165 0 0 489 888 0 0 385 906 0 0 316 892 0 0 490 708 0 0 384 839 0 0 315 832 1 2 3　临界灵敏度法当已知系统的临界比例增益 K C 和振荡周期 T C 时, 也可用经验整定公式来确定 P ID 控制器的参数。例如: K P = 0 T I= 0 T D = 0 6K C 5T C 125T C (2- 5) 特征参数 T C 和 K C, 一般由系统整定试验确定。或者用频率特性分析算法据受控过程 G P (S ) 直接算得 K C 和 T C, 即由增益裕量 gm 确定 K C, 由相位剪切频率 C 确定 T C: T C= 2 C K C= 10 (gm 20) 2 2　仿真试验法 (2- 6) 当受控过程的模型已知时, P ID 参数可通过数字仿真试验来确定。常见的有两种方式: 半自动的和全自动的。所谓半自动的方式, 就是由人来设置并调整 P ID 参数, 由计算机来仿真系统动态特性和计算系统的性能指标。所谓全自动的方式就是调整 P ID 参数的任务也由计算机来完成, 一般用最优化算法来整定 P ID 参数。对于单参数的 P 控制器常用黄金分割算法。对于多参数的 P I 和 P ID 控制器常用单纯 1997 年第 4 期　　　　　　　　　　　　工业仪表与自动化装置 ·36· 形优化算法。优化性能指标常选 IA E 或 ISE, 一个全自动的 P ID 参数优化 CAD 系统如图 2—2 所示。图 2- 2　P ID 控制器参数优化 CAD 程序框图 m -Ha gglund 自整定 P ID 3　 stro 控制结构　　由前面的讨论可知, 若测出了系统的一阶模型 (式 2—1) 或得出了系统的振荡频率 C 和增益 K C, 则可以容易地设计出 P ID 控制器。以往要想求出系统的这些特征参数, 需要使用离线的方法来进行, 即首先通过试验测出系统的特征参数, 然后再根据这些参数设计一个合适的 P ID 控制器, 最后再将此控制器应用到原系统的控制中。若系统的参数发生变化, 则应该再重新开始这一过程。 m H a stro gg lund 提出了一种继电型 P ID 自整定控制结构, 该方案的基本想法是在控制系统中设置两种模态; 测试模态和调节模态, 在测试模态下由一个继电非线性环节来测试系统的振荡频率和增益, 而在调节模态下由系统的特证参数首先得出 P ID 控制器, 然后由此控制器对系统的动态性能进行调节。如果系统的参数发生变化时, 则需要重新进入测试模态进行测试, 测试完成之后再回到调节模态进行控制。继电型 P ID 自整定控制结构如图 3—1 所示。从图中可以看出, 两个模态之间的切换是靠

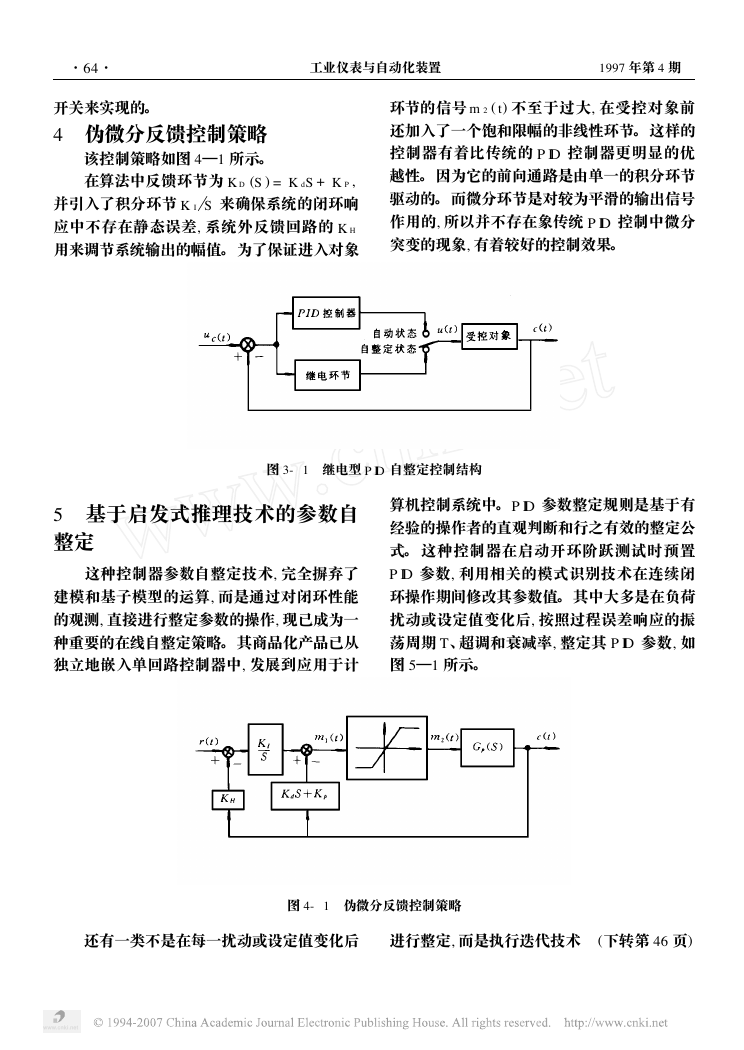
·46· 工业仪表与自动化装置　　　　　　　　　　　　1997 年第 4 期开关来实现的。 4　伪微分反馈控制策略　　该控制策略如图 4—1 所示。　　在算法中反馈环节为 K D (S ) = K dS + K P , 并引入了积分环节 K I S 来确保系统的闭环响应中不存在静态误差, 系统外反馈回路的 K H 用来调节系统输出的幅值。为了保证进入对象环节的信号 m 2 ( t) 不至于过大, 在受控对象前还加入了一个饱和限幅的非线性环节。这样的控制器有着比传统的 P ID 控制器更明显的优越性。因为它的前向通路是由单一的积分环节驱动的。而微分环节是对较为平滑的输出信号作用的, 所以并不存在象传统 P ID 控制中微分突变的现象, 有着较好的控制效果。图 3- 1　继电型 P ID 自整定控制结构 5　基于启发式推理技术的参数自整定　　这种控制器参数自整定技术, 完全摒弃了建模和基子模型的运算, 而是通过对闭环性能的观测, 直接进行整定参数的操作, 现已成为一种重要的在线自整定策略。其商品化产品已从独立地嵌入单回路控制器中, 发展到应用于计算机控制系统中。P ID 参数整定规则是基于有经验的操作者的直观判断和行之有效的整定公式。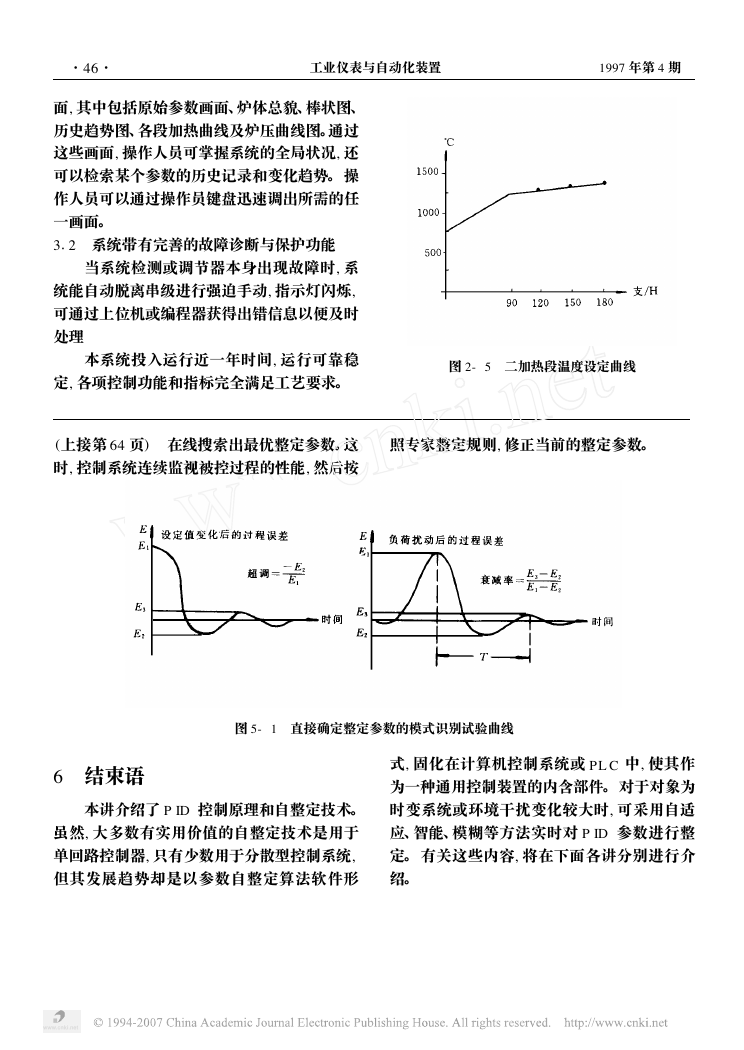这种控制器在启动开环阶跃测试时预置 P ID 参数, 利用相关的模式识别技术在连续闭环操作期间修改其参数值。其中大多是在负荷扰动或设定值变化后, 按照过程误差响应的振荡周期 T、超调和衰减率, 整定其 P ID 参数, 如图 5—1 所示。　　还有一类不是在每一扰动或设定值变化后进行整定, 而是执行迭代技术 (下转第 46 页) 图 4- 1　伪微分反馈控制策略

·64· 工业仪表与自动化装置　　　　　　　　　　　　1997 年第 4 期面, 其中包括原始参数画面、炉体总貌、棒状图、历史趋势图、各段加热曲线及炉压曲线图。通过这些画面, 操作人员可掌握系统的全局状况, 还可以检索某个参数的历史记录和变化趋势。操作人员可以通过操作员键盘迅速调出所需的任一画面。 3 2　系统带有完善的故障诊断与保护功能当系统检测或调节器本身出现故障时, 系统能自动脱离串级进行强迫手动, 指示灯闪烁, 可通过上位机或编程器获得出错信息以便及时处理本系统投入运行近一年时间, 运行可靠稳定, 各项控制功能和指标完全满足工艺要求。图 2- 5　二加热段温度设定曲线 (上接第 64 页) 　在线搜索出最优整定参数。这时, 控制系统连续监视被控过程的性能, 然后按照专家整定规则, 修正当前的整定参数。图 5- 1　直接确定整定参数的模式识别试验曲线 6　结束语　　本讲介绍了 P ID 控制原理和自整定技术。虽然, 大多数有实用价值的自整定技术是用于单回路控制器, 只有少数用于分散型控制系统, 但其发展趋势却是以参数自整定算法软件形式, 固化在计算机控制系统或 PL C 中, 使其作为一种通用控制装置的内含部件。对于对象为时变系统或环境干扰变化较大时, 可采用自适应、智能、模糊等方法实时对 P ID 参数进行整定。有关这些内容, 将在下面各讲分别进行介绍。

·05· 工业仪表与自动化装置　　　　　　　　　　　　1997 年第 5 期新型 P ID 控制及其应用第二讲　自适应 P ID 控制陶永华华东冶金学院　马鞍山: 243002 1　引言　　所谓自适应控制 (A dap tive con tro l) 就是在控制对象未知的情况下, 或者控制对象的参数发生变化时, 调整控制器的控制方法或参数, 使控制系统达到预定的控制品质。自适应控制的研究是从 50 年代开始的, 由于计算机的迅速发展及随机控制理论、系统辨识等学科的发展, 大大促进了自适应控制的研究。自适应控制与 P ID 控制器相结合, 形成了所谓自适应 P ID 控制或自校正 P ID 控制技术 (人们统称为自适应 P ID 控制)。自适应 P ID 控制具有自适应控制与普通 P ID 控制器两方面的优点: 首先, 它是自适应控制器, 就是说, 它有自动辨识被控过程参数、自动整定控制器参数、能够适应被控过程参数的变化等一系列优点; 其次, 它又具有常规 P ID 控制器结构简单、鲁棒性好、可靠性高、为现场工作人员和设计工程师们所熟悉的优点。自适应P ID 控制所具有的这两大优势, 使得它成为过程控制的一种较理想的自动化装置, 成为人们竞相研究的对象和自适应控制发展的一个方向。自适应 P ID 控制器可分为 5 大类, 一类基于被控过程参数辨识, 统称为参数自适应 P ID 控制器, 其参数的设计依赖于被控过程模型参数的估计。另一类基于被控过程的某些特征参数, 诸如临界振荡增益 K C、临界振荡频率等。这种类型的自适应 P ID 控制没有一个统一名称, 我们姑且称为非参数自适应 P ID 控制器。其参数的设计直接依赖于过程的特征参数 C 和一些工程上常用的经验整定规则。如果按控制器参数设计的原理来分, 自适应 P ID 控制器又可分为五大类, 它们是: 极点配置自适应 P ID 控制器、相消原理自适应 P ID 控制器、基于经验规则的自适应 P ID 控制器、基于二次型性能指标的自适应 P ID 控制器和智能或专家自适应 P ID 控制器。本讲着重介绍极点配置自适应 P ID 控制和一些具有应用前景的 P ID 自适应控制系统。 2　极点配置自适应 P ID 控制　　极点配置自适应控制算法由W ellstead 等人在 1979 年首先提出, 继而由 m 和 w it tenm ark, V ogel 和 Edgar, E llio tt 等人改进和深化, 成为自适应控制中的一个重要组成部分, W ittenm ark 和 m 等人在此基础上提出了极点配置自适应 P ID 控制算法。 stro stro 设受控过程的数学模型可用 CA RM A M oving R eg ressive A u to ( Con tro lled A verage) 受控自回归滑动平均模型描述: 　A (Z - 1) y (t) = Z - dB (Z - 1) u ( t) + C (Z - 1) ( t) (2—1) 　　其中 y ( t)、u ( t)、 (t) 分别为被控对象的输出、输入和不可测的扰动噪声; Z - 1为滞后一步算子, 即 Z - 1y ( t) = y ( t- 1) ; d 为滞后步数; A (Z - 1)、B (Z - 1)、C (Z - 1) 均为 Z - 1的多项式: 　 A (Z - 1) = 1+ a1Z - 1+ …+ anaZ - na B (Z - 1) = b 0+ b 1Z - 1+ …+ bnbZ - nb C (Z - 1) = 1+ c1Z - 1+ …+ cncZ - nc (b0≠0) (2—2)

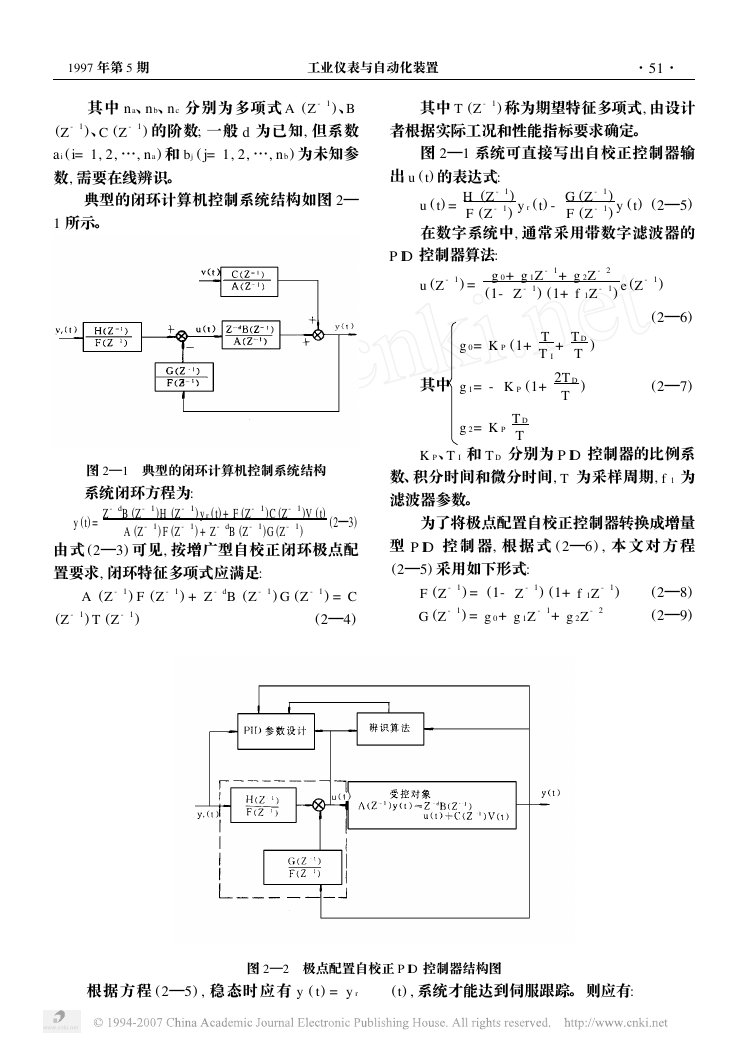
1997 年第 5 期　　　　　　　　　　　　工业仪表与自动化装置 ·15· 　　其中 na、nb、nc 分别为多项式 A (Z - 1)、B (Z - 1)、C (Z - 1) 的阶数; 一般 d 为已知, 但系数 a i (i= 1, 2, …, na) 和 bj ( j= 1, 2, …, n b) 为未知参数, 需要在线辨识。典型的闭环计算机控制系统结构如图 2— 1 所示。　　其中 T (Z - 1) 称为期望特征多项式, 由设计者根据实际工况和性能指标要求确定。图 2—1 系统可直接写出自校正控制器输出 u ( t) 的表达式: H (Z - 1) F (Z - 1) y r (t) - G (Z - 1) F (Z - 1) y (t) (2—5) u ( t) = 在数字系统中, 通常采用带数字滤波器的 P ID 控制器算法: u (Z - 1) = g 0+ g 1Z - 1+ g 2Z - 2 (1- Z - 1) (1+ f 1Z - 1) e (Z - 1) ) (2—6) (2—7) g 0= K P (1+ T T I 其中 g 1= - K P (1+ g 2= K P T D T + T D T 2T D T ) 　　K P、T I 和 T D 分别为 P ID 控制器的比例系数、积分时间和微分时间, T 为采样周期, f 1 为滤波器参数。为了将极点配置自校正控制器转换成增量型 P ID 控制器, 根据式 ( 2—6) , 本文对方程 (2—5) 采用如下形式: F (Z - 1) = (1- Z - 1) (1+ f 1Z - 1) 　　G (Z - 1) = g 0+ g 1Z - 1+ g 2Z - 2 (2—8) (2—9) 图 2—1　典型的闭环计算机控制系统结构　　系统闭环方程为: y (t) = Z - dB (Z - 1)H (Z - 1) y r (t) + F (Z - 1)C (Z - 1)V (t) A (Z - 1) F (Z - 1) + Z - dB (Z - 1)G (Z - 1) (2—3) 由式 (2—3) 可见, 按增广型自校正闭环极点配置要求, 闭环特征多项式应满足: A (Z - 1) F (Z - 1) + Z - dB (Z - 1) G (Z - 1) = C (2—4) (Z - 1) T (Z - 1) 　　根据方程 (2—5) , 稳态时应有 y ( t) = y r ( t) , 系统才能达到伺服跟踪。则应有: 图 2—2　极点配置自校正 P ID 控制器结构图

分享到：

赞收藏

资料库

新型PID控制及其应用(共六讲).pdf

相关推荐

课程资源

热门标签

最新资料