2022年湖南娄底中考数学试题及答案.doc

发布时间：2022-10-13 发布人：admin 分类：说明书资料大小：3.33M 资料格式：doc 举报版权申诉

第1页 / 共27页

第2页 / 共27页

第3页 / 共27页

第4页 / 共27页

第5页 / 共27页

第6页 / 共27页

第7页 / 共27页

第8页 / 共27页

文本预览

2022 年湖南娄底中考数学试题及答案一、选择题（本大题共 2 小题，每小题 3 分，满分 36 分，每小题给出的四个选项中，只有一个选项是符合题目要求的，请把你认为符合题目要求的选项填涂在答题卡上相应題号下的方框里） 1. 2022 的倒数是（） A. 2022 C. 1 2022 【答案】C B. 2022  D.  1 2022 2. 下列式子正确的是（） A. 3 a a  2  5 a C.  ab 2 ab 2 【答案】A B.  32 a 5 a D. 3 a  2 a  5 a 3. 一个小组 10 名同学的出生年份（单位：月）如下表所示：编号月份 1 2 2 6 3 8 4 6 5 10 6 4 7 7 8 8 9 8 10 7 这组数据（月份）的众数是（） A. 10 B. 8 C. 7 D. 6 【答案】B 4. 下列与 2022 年冬奥会相关的图案中，是中心对称图形的是（）

B. D. A. C. 【答案】D 5. 截至 2022 年 6 月 2 日，世界第四大水电站——云南昭通溪洛渡水电站累计生产清洁电能突破 5000 亿千瓦时，相当于替代标准煤约 1.52 亿吨，减排二氧化碳约 4.16 亿．5000 亿用科学记数法表示为（） A. 10 50 10 C. 12 0.5 10 【答案】B B. 11 5 10 D. 12 5 10 6. 一条古称在称物时的状态如图所示，已知 1 80    ，则 2  （） A. 20 B. 80 C. 100 D. 120

【答案】C 7. 不等式组 3 x   2  ＞   x  1 2 的解集在数轴上表示正确的是（） A. C. 【答案】C B. D. 8. 将直线 2 x y 1  向上平移 2 个单位，相当于（） A. 向左平移 2 个单位 B. 向左平移 1 个单位 C. 向右平移 2 个单位 D. 向右平移 1 个单位【答案】B 9. 在古代，人们通过在绳子上打结来计数．即“结绳计数”．当时有位父亲为了准确记录孩子的出生天数，在粗细不同的绳子上打结（如图），由细到粗（右细左粗），满七进一，那么孩子已经出生了（） A. 1335 天 B. 516 天 C. 435 天 D. 54 天 10. 如图，等边 ABC 内切的图形来自我国古代的太极图，等边三角形内切圆中的黑色部分和白色部分关于等边 ABC 的内心成中心对称，则圆中的黑色部分的面积与 ABC 的面

积之比是（） A. 3  18 【答案】A B. 3 18 C. 3  9 D. 3 9 11. 在平面直角坐标系中，O 为坐标原点，已知点  P m 、  ,1 1,Q m （  0m  且 1m  ），过点 P 、Q 的直线与两坐标轴相交于 A 、B 两点，连接OP 、OQ ，则下列结论中成立的是（） ①点 P 、Q 在反比例函数 ③ 0    POQ  my  的图象上；② AOB x  ；④ POQ 的值随 m 的增大而增大．  90 成等腰直角三角形； A. ②③④ B. ①③④ C. ①②④ D. ①②③ 【答案】D 12. 若10x N ，则称 x 是以 10 为底 N 的对数．记作： lg N x ．例如： 210 100 ，则 2 lg100  ； 010 1 ，则 0 lg1 ．对数运算满足：当 0M  ， 0N  时， lg M  lg N  lg  MN  ，例如：lg3 lg5 lg15   ，则 lg5 2  lg5 lg 2 lg 2  的值为（）  A. 5 B. 2 C. 1 D. 0 【答案】C 二、填空题（本大题共 6 小题，每小题 3 分，满分 18 分）

的自变量 x 的取值范围是_______． 13. 函数 y  1 x  1 【答案】 1x  【分析】由 1 1x  有意义可得： 1 0, x   再解不等式可得答案．【详解】解：由 1 1x  有意义可得： , 即 1 0, x   1 0 x ì - ³ ï í 1 ï - ¹ î x 0 解得： 1. x  故答案为： 1x  14. 已知实数 1 ,x x 是方程 2 x 2 x   的两根，则 1 2x x  ______． 1 0 【答案】 1 【分析】由一元二次方程根与系数的关系直接可得答案．【详解】解： 实数 1 ,x x 是方程 2 x 2 x   的两根， 1 0 \ x x 1 2 = 1 - 1 1, = - 故答案为： 1 15. 黑色袋子中装有质地均匀，大小相同的编号为 1~15 号台球共 15 个，搅拌均匀后，从袋中随机摸出 1 个球，则摸出的球编号为偶数的概率是_______．【答案】 7 15 【分析】根据概率公式求解即可．

【详解】解：由题意可知：编号为 1~15 号台球中偶数球的个数为 7 个， ∴摸出的球编号为偶数的概率故答案为： 7 15 ． 7= 15 ， 16. 九年级融融陪同父母选购家装木地板，她感觉某品牌木地板拼接图（如实物图）比较美观，通过手绘（如图）、测量、计算发现点 E 是 AD 的黄金分割点，即 DE  0.618 AD ．延长 HF 与 AD 相交于点G ，则 EG  ________ DE .（精确到 0.001）【答案】0.618 【分析】设每个矩形的长为 x，宽为 y，则 DE＝AD－AE＝x－y，四边形 EFGM是矩形，则 EG ＝MF＝y，由 DE  0.618 AD 得 x－y≈0.618x，求得 y≈0.382x，进一步求得 EG DE ，即可得到答案．【详解】解：如图，设每个矩形的长为 x，宽为 y，则 DE＝AD－AE＝x－y，由题意易得∠GEM＝∠EMF＝∠MFG＝90°， ∴四边形 EFGM是矩形， ∴EG＝MF＝y， ∵ DE  0.618 AD ， ∴x－y≈0.618x，解得 y≈0.382x，

∴ EG DE  y  x y ≈ 0.382  x 0.382 x x  0.618 ， ∴EG≈0.618DE．故答案为：0.618． 17. 菱形 ABCD 的边长为 2， ABC  45  ，点 P 、Q 分别是 BC 、BD 上的动点，CQ PQ 的最小值为______．【答案】 2 【分析】过点 C作 CE⊥AB于 E，交 BD于 G，根据轴对称确定最短路线问题以及垂线段最短可知 CE为 FG+CG的最小值，当 P与点 F重合，Q与 G重合时，PQ+QC最小，在直角三角形 BEC中，勾股定理即可求解．【详解】解：如图，过点 C作 CE⊥AB于 E，交 BD于 G，根据轴对称确定最短路线问题以及垂线段最短可知 CE为 FG+CG的最小值，当 P与点 F重合，Q与 G重合时，PQ+QC最小，

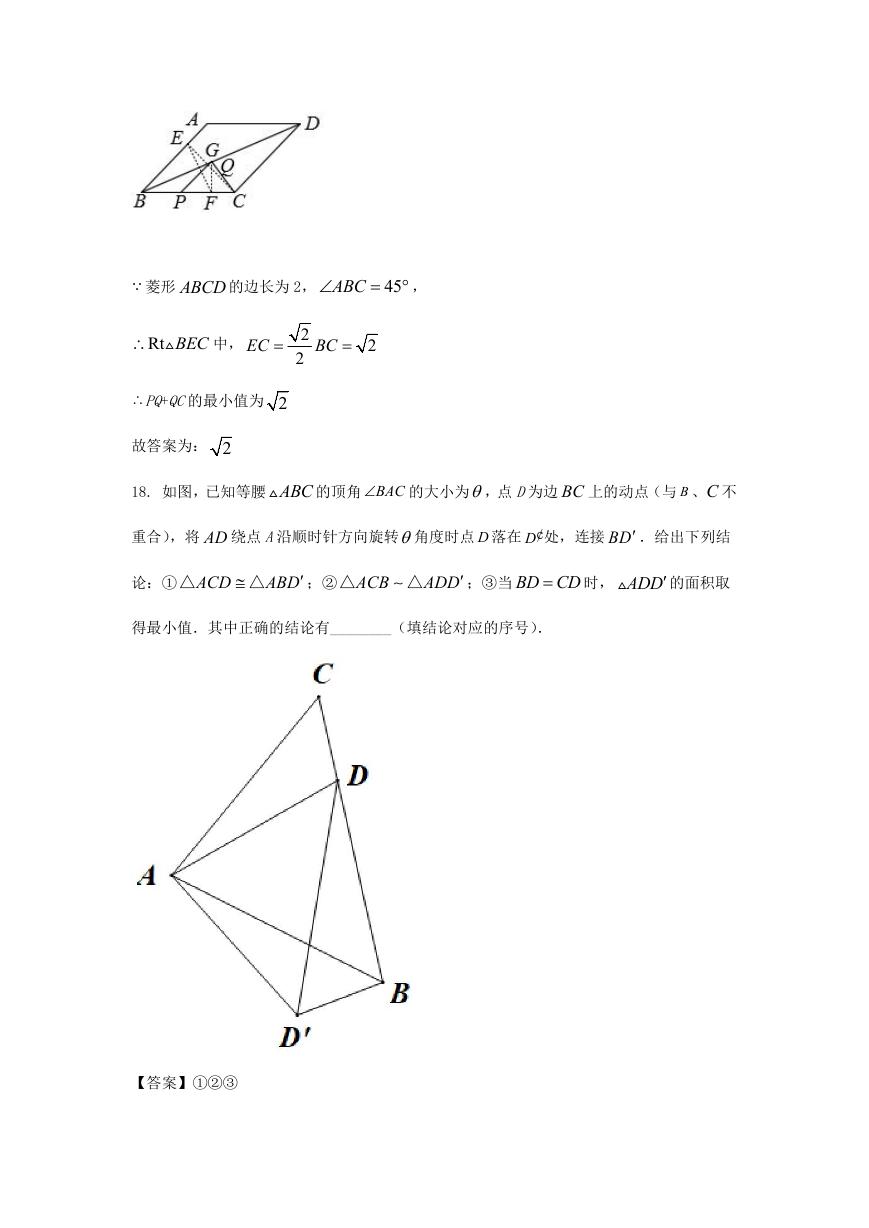
 菱形 ABCD 的边长为 2， ABC  45  ，   Rt BEC 中， EC  2 2 BC  2 PQ+QC的最小值为 2 故答案为： 2 18. 如图，已知等腰 ABC 的顶角 BAC 的大小为，点 D为边 BC 上的动点（与 B 、C 不重合），将 AD 绕点 A沿顺时针方向旋转角度时点 D 落在 D¢处，连接 BD ．给出下列结论：① ACD △  △ ABD ；② ACB △  △ ADD ；③当 BD CD 时， ADD  的面积取得最小值．其中正确的结论有________（填结论对应的序号）．【答案】①②③

分享到：

赞收藏

资料库

2022年湖南娄底中考数学试题及答案.doc

相关推荐

中考

热门标签

最新资料