LMS自适应滤波器仿真 我们考虑如图1所示的横式滤波器。 其输入矢量为: 图1. 横式滤波器 ( ) X n   ( ), [ ( ), x n x n x  2 1 1), [ ( ), ( x n x n   T ( )] n M ( x n M   1)] T 其滤波器参数(即加权系数)矢量为: w  则滤波器的输出为: ( ) ( ) y n W X n  w w 1  W [ , , 2 T T ( ) X n W y(n)相对于需要信号d(n)的误差为: ( ) ( ) d n W X n ( ) d n ( ) y n ( ) e n －     T ]T M 根据最小均方误差准则，最佳滤波器参数 optw 应当使   2{ ( )} E e n 最小，通 过推导，均方误差可以表示为:   ＝ 2{ E d n { ( ) ( )} E x n d n xdr  ( )} 2 T W r W R W  T xd xx xxR  { E X n X ( ) T ( )} n 其中 为 x（n）的自相关矩阵。可以看出均方误差为W的二次函数，且其矩阵 xxR 是正定或 半正定的，所以它一定有最小值。由于它对W的梯度为零，所以取最小值时 optW 应满 为x(n)和d（n）的互相关矢量， 足 0  。当 xxR 为满秩时，可以得到唯一解: 根据上述公式，由输入x(n)和d(n)得到 xxR 和 xdr 的估计值就可以计算出最佳权矢 量 optW 。但是由于涉及到求逆运算，运算量很大，特别是在加权系数的个数大而且 需要实时、高速地自适应滤波时，这种方法显然不太实用。 opt 1 R r xx xd W  最佳权矢量 optW 。可以由另一个重要方法求得，即最陡梯度下降法。按照这种 

方法，每次迭代权矢量W(n)沿着梯度  的负方向修正，亦即如果第n次迭代的权矢 量为W(n)，则第n+l次迭代的权矢量等于:   1) ( ) w n ( w n 其中u为常数并被称为步长因子或收敛因子。的梯度  常常缺乏计算的条件。 u    在LMS算法中，可以用瞬时平方误差的梯度 2[ ( ) ( )] 2 ( ) e n e n X n    ( 1) W n   2[ ( )] e n    ，得到 ( ) ( ) ( ) 2 W n uX n e n  为: 。 2[ e n  ( )] 来代替均方误差的梯度 。这样LMS算法的更新权矢量的递推公式 现仿真AR（2）模型的LMS自适应滤波器。 1)   ( ) x n 其AR（2）模型的表达式为 2 (0, ) N  ( a x n 1 ( ) V n   。 白噪声，分布满足 ( a x n 2  2)  ( ) V n ，其中 ( )V n 为高斯 LMS自适应滤波器的结构图如下： LMS算法的更新权矢量的递推公式为: ( 1) ( ) uX n e n  ( 2) ( ) uX n e n  ( W n W n ( W n W n 1) 2   1) 2   ( ) ( )   1 1 2 2 。 其中参数设置x(-1)=x(-2)=0, w(-1)=w(-2)=0,u=0.4 ,a1= -0.25 , a2= 1.1, 2 =0.0965 程序实现为： clear all; u=0.4; n=2000; a1=-0.25; a2=1.1; a3=[1 -a1 -a2]; b1=1; m1=randn(1,n); m1=m1/std(m1); 

m1=m1-mean(m1); a=0; b=sqrt(0.0965); m1=a+b*m1; [x zf]=filter(b1,a3,m1); w1(1)=0;w2(1)=0; e(1)=x(1);e(2)=x(2)/(1+(2*u*x(1)*x(1)));%e(2)=x(2)-w1(2)*x(1); w1(2)=2*u*e(2)*x(1); w2(2)=0; for i=3:n e(i)=(x(i)-(x(i-1)*w1(i-1))-(x(i-2)*w2(i-1)))/(1+(2*u*x(i-1)*x(i-1)) +(2*u*x(i-2)*x(i-2))); w1(i)=w1(i-1)+2*u*e(i)*x(i-1); w2(i)=w2(i-1)+2*u*e(i)*x(i-2); end m=1:n; figure(1); plot(m,w1,':',m,w2); title('Weight Estimation ') ; xlabel('Iteration Number') ; ylabel('Weight') ; legend('W1 Estimation','W2 Estimation') figure(2); plot(m,abs(e)); title('Learning Curve') ; xlabel('Iteration Number') ; ylabel('Output Estimation Error') ; 

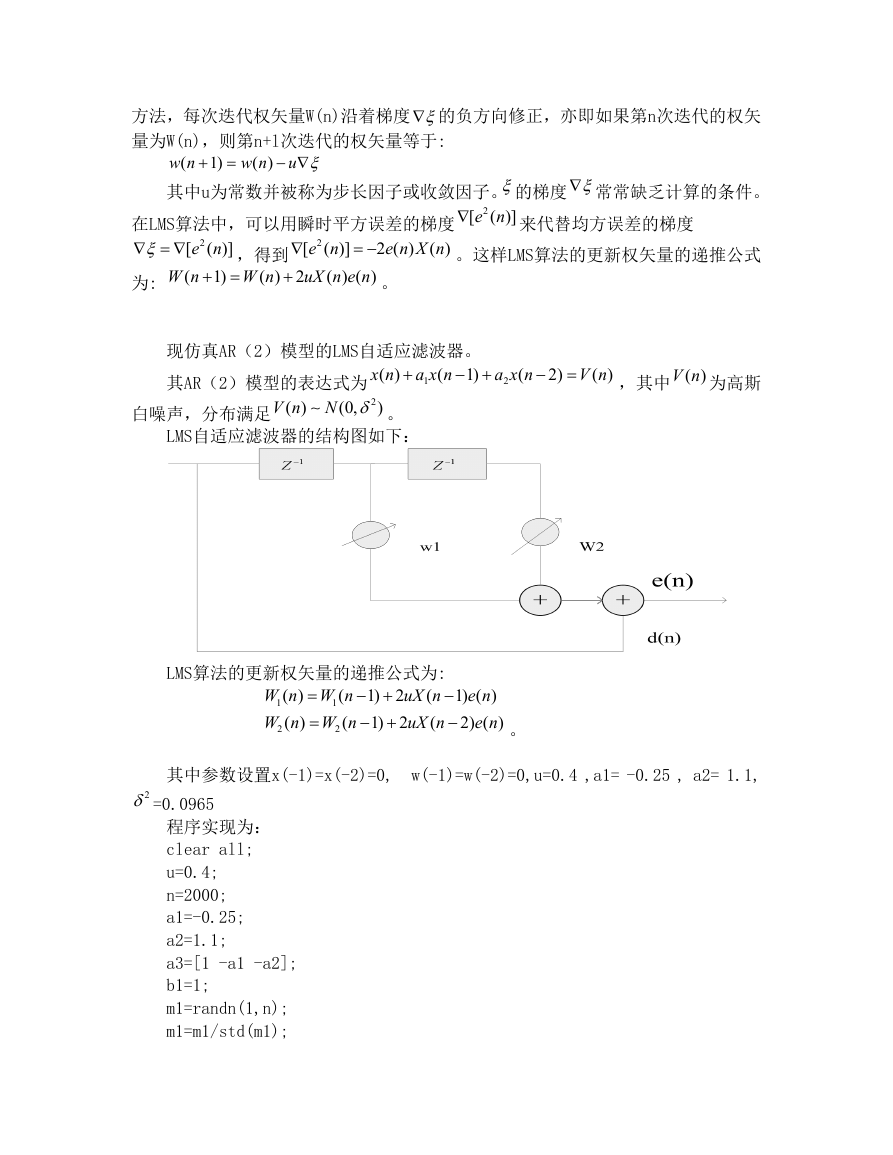
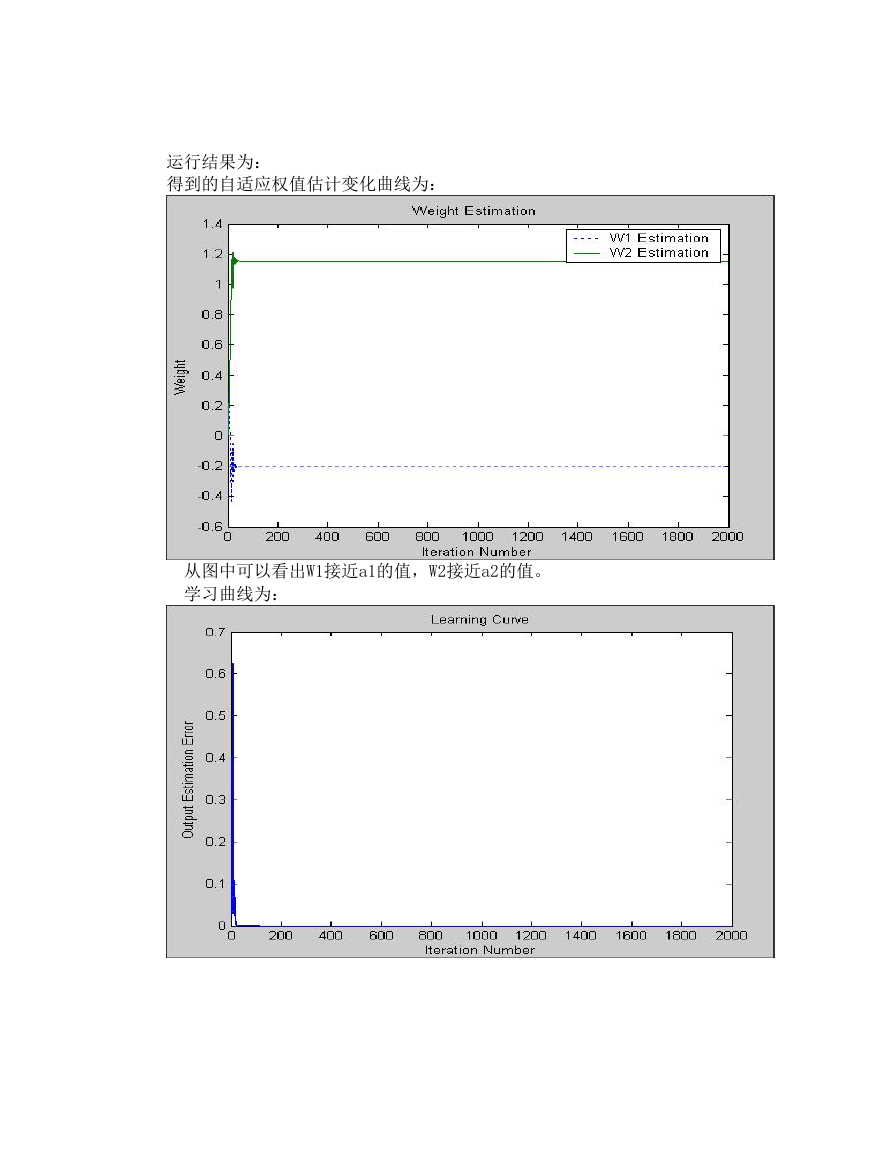
运行结果为： 得到的自适应权值估计变化曲线为： 从图中可以看出W1接近a1的值，W2接近a2的值。 学习曲线为：