论文研究-多用户MIMO系统中的预编码技术研究 .pdf-资料库

5 10 15 20 25 30 35 40 中国科技论文在线 http://www.paper.edu.cn 多用户 MIMO 系统中的预编码技术研究贺美琛，啜钢** （北京邮电大学信息与通信工程学院，北京 100876）摘要：多用户 MIMO 系统中的预编码技术，可以有效地抑制用户间的共信道干扰，提高系统容量。通常预编码的设计要求获得发射端的理想信道信息，而实际环境中，接收端的信道估计误差和反馈信息的传输时延，使得收发端只能得到部分信道信息。本文首先对理想信道信息下的预编码进行了综述和分析，并在此基础上分析探讨了非理想信道信息下的预编码，通过 matlab 对理想和非理想信道信息下的预编码进行了仿真，对于信道估计误差对预编码系统的影响研究具有重要意义。关键词：预编码；多用户 MIMO；非理想信道信息中图分类号：TN929.5 Research on Multi-user MIMO Precoding Technique He Meichen, Chuai Gang (School of Information and Communication Engineering,Beijing University of Posts and Telecommunications, Beijing 100876) Abstract: Precoding technique in multi-user MIMO systems can effectively reduce the interference between users sharing the same wireless channel and therefore increase systems' capacity. Generally speaking, precoding demands transmitting terminals to acquire the perfect channel information. But in real environments, only part of the channel information can be acquired at the receiver due to channel estimation errors. In addition, the channel information feedback to the transmitters is delayed because of the transmission time through air interface. In this paper, we first overviewed and analyzed the precoding technologies with perfect channel information. On this basis, we moved on to analyze and discuss precoding with imperfect channel information. Precoding with both perfect and imperfect channel information are simulated with Matlab. Our conclusions give significant insights into the influence of channel estimation errors on BER performances in multi-user MIMO communication systems with precoding. Keywords: Precoding; Multi-user MIMO; Imperfect CSI 0 引言在多用户 MIMO 系统中，系统的容量与用户的数目成线性关系，这在理论上为 MIMO 系统的发展指明了方向，同时引入了一个不可避免的难题，多用户之间的干扰消除，预编码作为解决这一问题的最佳途径，引起了学者们的广泛关注。面向接收端的预编码技术在发射端利用信道状态信息对信号进行预处理，可以有效地消除广播信道的多用户干扰，大大提高系统容量[1]；可以大大简化接收机的算法，解决移动台的功耗和体积问题；由于发射端能准确知道各用户的数据，所以在发射端采用反馈干扰抵消的方法，不存在误码扩散问题，性能更优。然而，在实际环境中，由于信道估计误差、估计时延、反馈误差、反馈时延等因素的影响，发射端很难获得完整的信道状态信息。尤其在 FDD 模式中，发射端要想获得完整的信道状态信息将大大增加反馈链路的负担[2]。因此，在发射端只知道部分信道状态信息的条件下，对多用户系统下行链路预编码的研究引起了人们极大的兴趣[3]。作者简介：贺美琛，（1987-），女，硕士，主要研究方向：移动通信。通信联系人：啜钢，（1959-），男，教授，主要研究方向：无线通信理论，移动通信网络性能分析和软件开发等。E-mail: chuai@bupt.edu.cn - 1 -

45 50 55 60 中国科技论文在线 1 理想信道信息下的预编码 1.1 迫零预编码算法 http://www.paper.edu.cn 线形预编码以简化收端为目的，将原来在接收端进行的处理搬到发送端进行。线形预编码的复杂度低，具有很高的实用性[4]。常见的线形预编码算法主要有迫零（Zero-forcing，ZF）预编码算法和最小均方误差（Minimum mean-square error，MMSE）预编码算法。ZF 预编码算法[5]在用户间干扰的抑制方面优于 MMSE 预编码算法，算法操作简单，为便于分析，本文以 ZF 预编码为线性预编码的代表来分析。图 1 迫零预编码系统迫零预编码系统如图 1 所示。首先把待发送的信息序列通过预编码矩阵进行运算，然后通过信道到达接收端，在接收端进行量化处理[6]。其中，x 为发送信号，a 为经过处理后的发送信号，y 为接收信号，F 为系统的预编码矩阵，H 为信道矩阵，n 为噪声，β为缩放因子。发送端经过于编码处理后的发送信号为： a=Fx （1）其中，预编码矩阵 F 为： F= -1Hβ （2）上式中，β为缩放因子，其作用是保证发送的预编码信号向量 a 的功率恒定。它的取 -1 值为： =β M ∑ = k M 1 （3） 1 2 ku 其中，M 为基站发送端天线数， kμ 是信道矩阵 H 的第 k 个特征值[7]。相应的，在接收 65 端信号再乘上缩放因子β作为补偿。接收信号为： β(H=y 1 β nxH ) 1 +− += x βn （4）由此可以看出，发送端根据信道状态信息矩阵 H 可以构造一个预编码矩阵 F。发送信号通过和矩阵 F 相乘实现在发送端的线性预编码。针对当前信道特性构成的预编码矢量通过信道后，不需要检测就可以直接通过解调得到发送信号。 1.2 Tomlinson-Harashima 预编码算法 70 源于 Costa 环的 TH 预编码是非线性预编码的典型技术，较之与线形预编码，它在系统的信道容量上得到了相当大的提高[8]。 - 2 -

中国科技论文在线 http://www.paper.edu.cn 75 图 2 TH 预编码系统 TH 预编码结构如图 2 所示[9]。其中，x 为发射信号，y 为接收信号，a 为信号 x 经过反馈取模之后的信号。F 为预编码矩阵，H 为信道矩阵，n 为噪声，G 为加权对角矩阵，B 为反馈矩阵。 80 为了方便分析，我们集中研究发送天线数等于接收天线数的情况（天线数均为 M），此时信道增益矩阵为方阵。首先对信道矩阵的转置 HH 做 QT 矩阵分解，可以得到: H = HSF （5）其中，S 为一个下三角矩阵，F 是一个酉阵。加权矩阵 G=diag ⎧ ⎨ ⎩ 为矩阵 S 的对角元素，k=1，…，M。取模是为了调整发射功率。 1 s 11 ,..., 1 s MM ⎫ ⎬ ⎭ ，这里 kks 根据 THP 结构中加权对角矩阵滤波器位置的不同，TH 预编码可以分为两种变体：加权对角矩阵 G 在基站端为集中式 THP，记为 cTHP 结构；加权对角矩阵 G 在用户端为分布式 THP，记为 dTHP 结构[10]。本文以 dTHP 结构为代表进行讨论，设定：B=GS。接收信号为：其中,a 为发送数据向量，是源向量 x 经过反馈滤波器 B 和取模器之后得到的，且满足 xB ( （6） G(HFa n)+ =y p ) -1 = + ，p 为模向量因子。 a 2 非理想信道信息下的预编码在实际应用中，通常采用训练序列对信道进行估计。在发送端发送一定数目的训练序列，接收端通过接收到的训练序列对信道状态进行估计，然后再将估计的信道状态信息反馈给发送端。由于信道状态估计误差和反馈时延等因素的影响，发送端不可能获得理想的信道状态信息。其中，信道状态的估计误差对系统的性能影响最为严重[11]。本文中，假设接收端和发送端拥有相同的信道信息，暂不考虑存在反馈时延的情形。假设信道为平坦衰落，且所有用户的信道都具有相同的大尺度功率衰落。定义 NK×M hσ 方差的复高斯随机变量，记，为独立同分布的 0 均值、 2 G(HFa n)+ =y 的信道矩阵为为 CN(0, 2 hσ )。非理想 CSI 可以建模为： 85 90 95 100 0 Δ （7）其中 HΔ 为 NK×M 的信道误差矩阵，即信道的估计误差，为了方便分析，我们假定 HΔ ,keσ )。因此，在基站发射 ,keσ 方差的复高斯随机变量，记为 CN(0， H+H=H 的第 k 行为 0 均值、 2 2 - 3 -

中国科技论文在线 http://www.paper.edu.cn 端和用户接收端的预编码模块的计算都是基于矩阵 H 而不是信道矩阵 0H 。 105 我们以接收端信号与干扰加噪声的比值 SINR 为性能指标，分析非理想 CSI 对预编码性能的影响。考虑如下情况：每个用户只有一根天线，而且总的接收天线数等于发射端天线数。另外，假定信道估计误差对各个发送是同分布的，即对于任意 k，满足假定功率平均分配。 2.1 迫零预编码算法 110 σ =, ke σ e 。为了方便分析，将（7）代入（4）中，可得到非理想信道信息下迫零预编码系统的接收信号为： β(H=y 0 1 β 1 − nxH + ) Δ−= x HH 1 − x + βn （8）将（8）代入（3）中，简化可得到： 1 uk 2 其中， kμ 是信道矩阵 H 的特征值，可得： σ M ( σσ ∑ R 1K = + = ZF ) M 2 X 2 E 2 N l （9） SINR ZF = 2 X ( σσ 2 E 2 X σ σ M 2 N + (10) 1 ku 2 ) M ∑ 1K = 2.2 Tomlinson-Harashima 预编码算法对 TH 预编码方法中的信道矩的转置 HH 做 QR 矩阵分解[12]，可以得到： (11) HSF H = 其中，S 为下三角阵，F 为酉阵。加权矩阵 G=diag ⎧ ⎨ ⎩ ，M。取模是为了调整发射功率。的对角元素，k=1， … 1 s 11 ,..., 1 s MM ⎫ ⎬ ⎭ ，这里 kks 为矩阵 S 对于 dTHP 结构，设定：B=GS 经过实际等效信道 0H 后，接收到的 1×M 信号 y 可以表示为： (12) 其中，a 为发送数据向量，是源向量 x 经过反馈滤波器 B 和取模器之后得到的，且满足 HFa G-px=y Δ Gn + + 115 120 125 G ，p 为模向量因子。X+p 为有效传输数据。 HFa Δ + Gn 为干扰加噪声项， (x1- = Ba 其自相关矩阵表达为： p) + = M eσ 2 IFF H = 1 。因此，可以得到如下近似表达式： dTHP R ≈ (M 2 σσσ n + 2 e 2 x )diag ⎧ ⎪ ⎨ ⎪⎩ 1 s 2 11 ,..., 1 2 MM s ⎫ ⎬ ⎭ （14） - 4 - GHF 由于 a 的幅度是受限于 x 的，所以此处可近似的得到 { HFaa dTHP R Δ H H H { GE= Δ H } + } H aaE { E Gnn 2σ≈ I x 。此外 H G }H (13) 130 1=HFF , { HHE ΔΔ 2 }

中国科技论文在线 http://www.paper.edu.cn 忽略取模运算的功率损失，则可以近似认为 x+p 相当于 x 的功率。从干扰噪声项的自相关矩阵可以看出，对每一行的发送数据而言，他们都有着各自的干扰噪声，并不相同。于是可以给出 k 行数据的 SINR 可以写成 SINR k dTHP = 2 X σ M 2 X σσ 2 E 1 s 2 kk + 2 n σ s 2 kk ，其中 k=1，2， … ，M。（15）从线性 ZF 预编码和 THP 的干扰噪声项的自相关矩阵 R 的表达式来看，两者的结构有所不同，ZF 预编码的每行数据的干扰和噪声是一致的，而 THP 中不同行数据的干扰和噪声是不同的。 3 仿真结果与分析本文假设 MIMO 系统有 4 根发射天线和 4 根接收天线，信道为准静态平坦衰落信道， 1=hσ ，为复高斯随机变量[13]。非理想信道条件下，信 eσ )，调制方式选择 QPSK。预编码技术分别采用线性 ZF 信道矩阵 0H 满足 i.i.d. CN(0，1),即道估计误差 HΔ 满足 i.i.d. CN(0，和 THP 算法。信道估计误差分别设为 1,0.1,0.01,0.001,0.0001。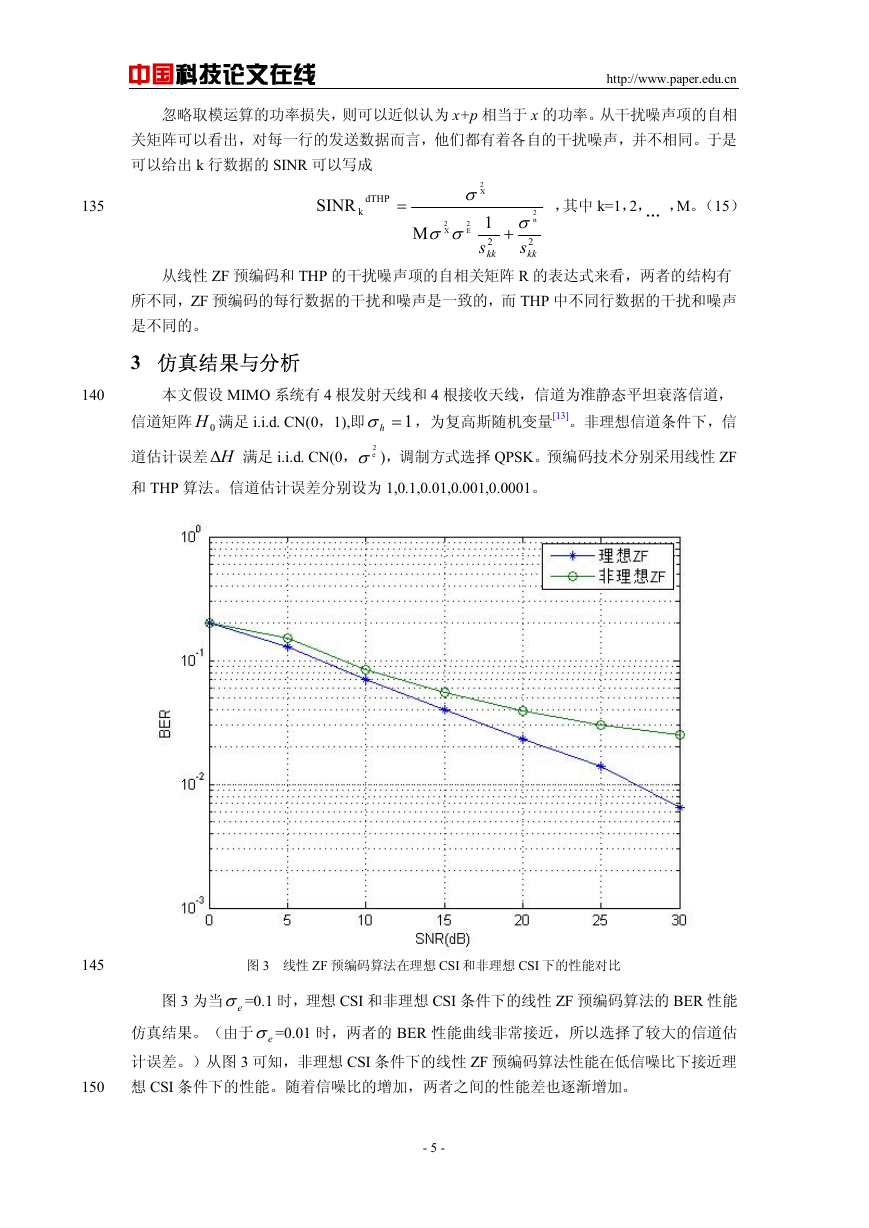 2 135 140 145 150 图 3 线性 ZF 预编码算法在理想 CSI 和非理想 CSI 下的性能对比图 3 为当 eσ =0.1 时，理想 CSI 和非理想 CSI 条件下的线性 ZF 预编码算法的 BER 性能仿真结果。（由于 eσ =0.01 时，两者的 BER 性能曲线非常接近，所以选择了较大的信道估计误差。）从图 3 可知，非理想 CSI 条件下的线性 ZF 预编码算法性能在低信噪比下接近理想 CSI 条件下的性能。随着信噪比的增加，两者之间的性能差也逐渐增加。 - 5 -

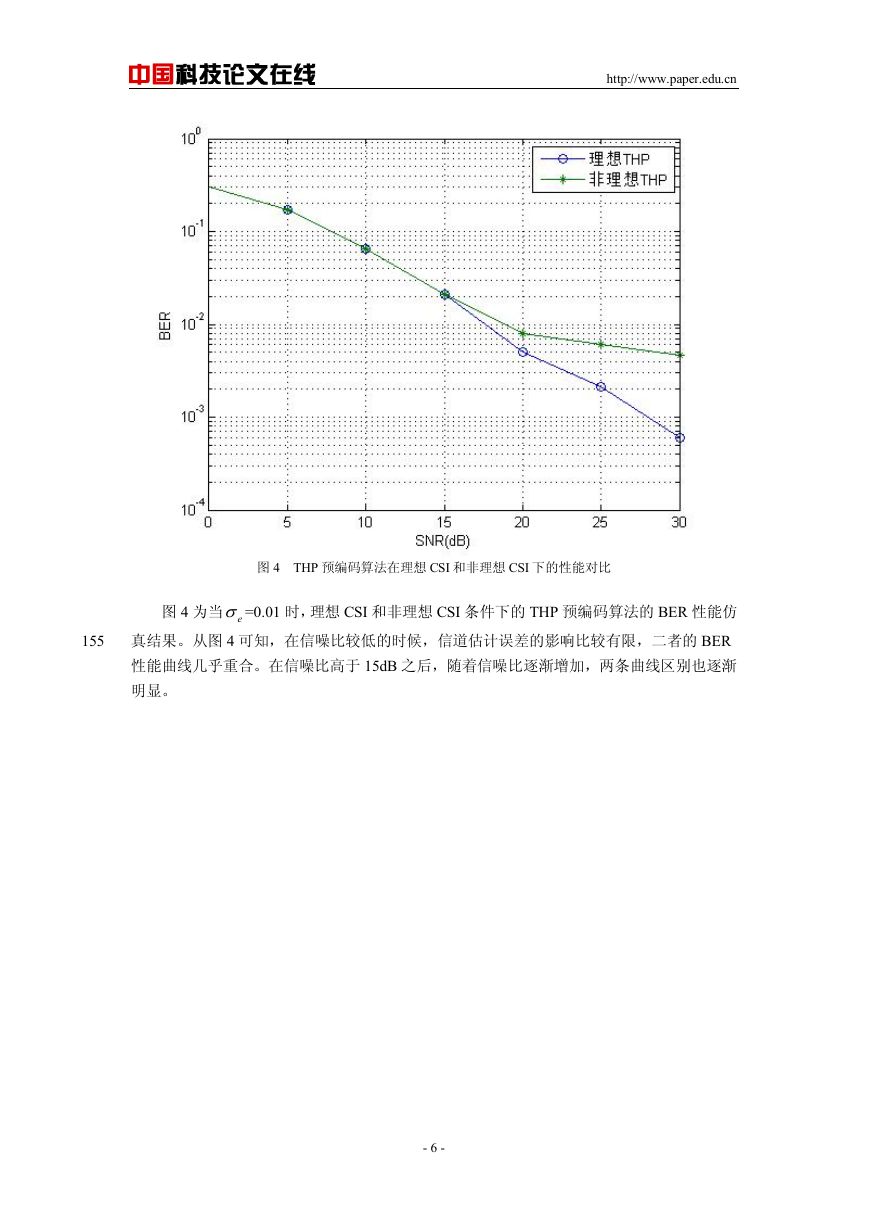
中国科技论文在线 http://www.paper.edu.cn 图 4 THP 预编码算法在理想 CSI 和非理想 CSI 下的性能对比 155 图 4 为当 eσ =0.01 时，理想 CSI 和非理想 CSI 条件下的 THP 预编码算法的 BER 性能仿真结果。从图 4 可知，在信噪比较低的时候，信道估计误差的影响比较有限，二者的 BER 性能曲线几乎重合。在信噪比高于 15dB 之后，随着信噪比逐渐增加，两条曲线区别也逐渐明显。 - 6 -

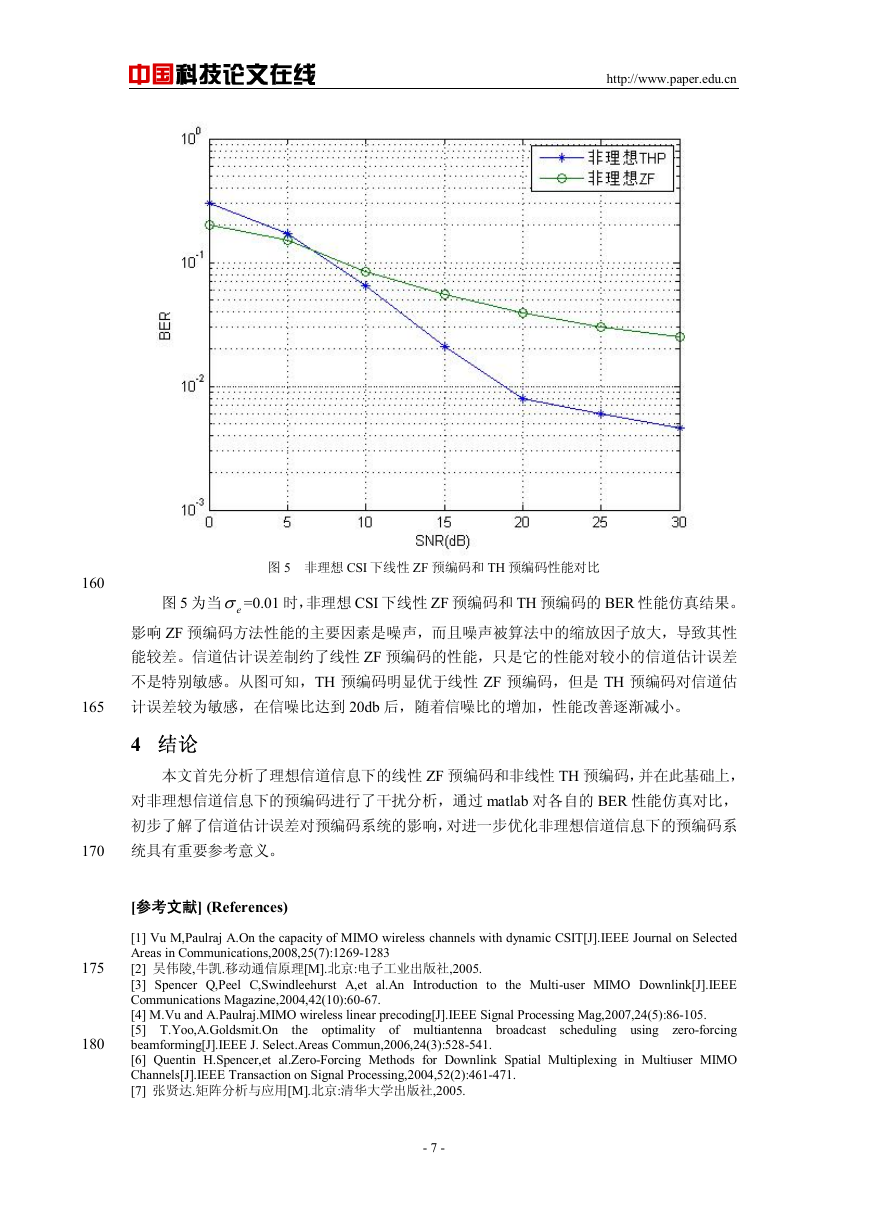
中国科技论文在线 http://www.paper.edu.cn 160 165 170 175 180 图 5 非理想 CSI 下线性 ZF 预编码和 TH 预编码性能对比图 5 为当 eσ =0.01 时，非理想 CSI 下线性 ZF 预编码和 TH 预编码的 BER 性能仿真结果。影响 ZF 预编码方法性能的主要因素是噪声，而且噪声被算法中的缩放因子放大，导致其性能较差。信道估计误差制约了线性 ZF 预编码的性能，只是它的性能对较小的信道估计误差不是特别敏感。从图可知，TH 预编码明显优于线性 ZF 预编码，但是 TH 预编码对信道估计误差较为敏感，在信噪比达到 20db 后，随着信噪比的增加，性能改善逐渐减小。 4 结论本文首先分析了理想信道信息下的线性 ZF 预编码和非线性 TH 预编码，并在此基础上，对非理想信道信息下的预编码进行了干扰分析，通过 matlab 对各自的 BER 性能仿真对比，初步了解了信道估计误差对预编码系统的影响，对进一步优化非理想信道信息下的预编码系统具有重要参考意义。 [参考文献] (References) [1] Vu M,Paulraj A.On the capacity of MIMO wireless channels with dynamic CSIT[J].IEEE Journal on Selected Areas in Communications,2008,25(7):1269-1283 [2] 吴伟陵,牛凯.移动通信原理[M].北京:电子工业出版社,2005. [3] Spencer Q,Peel C,Swindleehurst A,et al.An Introduction to the Multi-user MIMO Downlink[J].IEEE Communications Magazine,2004,42(10):60-67. [4] M.Vu and A.Paulraj.MIMO wireless linear precoding[J].IEEE Signal Processing Mag,2007,24(5):86-105. [5] T.Yoo,A.Goldsmit.On beamforming[J].IEEE J. Select.Areas Commun,2006,24(3):528-541. [6] Quentin H.Spencer,et al.Zero-Forcing Methods for Downlink Spatial Multiplexing in Multiuser MIMO Channels[J].IEEE Transaction on Signal Processing,2004,52(2):461-471. [7] 张贤达.矩阵分析与应用[M].北京:清华大学出版社,2005. the optimality of multiantenna broadcast scheduling using zero-forcing - 7 -

中国科技论文在线 http://www.paper.edu.cn 185 190 [8] Yu Fu and et,al.A Novel Nonlinear Precoding Algorithm for the Downlink of Multiple Antenna Multi-user System[J].IEEE VTC,2008,57:2189-2204. [9] 许道峰，黄永明，杨绿溪.多用户 MIMO 系统 TH 预编码[J].电子与信息学报，2009，3（3）：657-660. [10] Kusume K.,Joham M.,Utschick W.etc.Efficient Tomlinson-Harashinma Precoding for Spatial Multiplexing on Flat MIMO Channel[J].IEEE International Conference on Communications.2005,3:2021-2025. [11] 赵谦.无线 MIMO 系统的容量及信道估计算法的研究[D].西安:西安科技大学,2005. [12] M.Huang,S.Zhou,J.Wang.Analysis of Tomlinson-Harashima Precoding in Multiuser MIMO Systems With Imperfect Channel State Information[J].IEEE Transactions on Vehicular Technology,2008,57(5): 2856-2867. [13] Gaire G,Shamai S.On the Achievable Throughput of a Multiantenna Gaussian Broadcast Channel[J].IEEE Trans on Inform Theory,2003,49(7):1691-1706. - 8 -

资料库

论文研究-多用户MIMO系统中的预编码技术研究 .pdf

相关推荐

开发技术

热门标签

最新资料