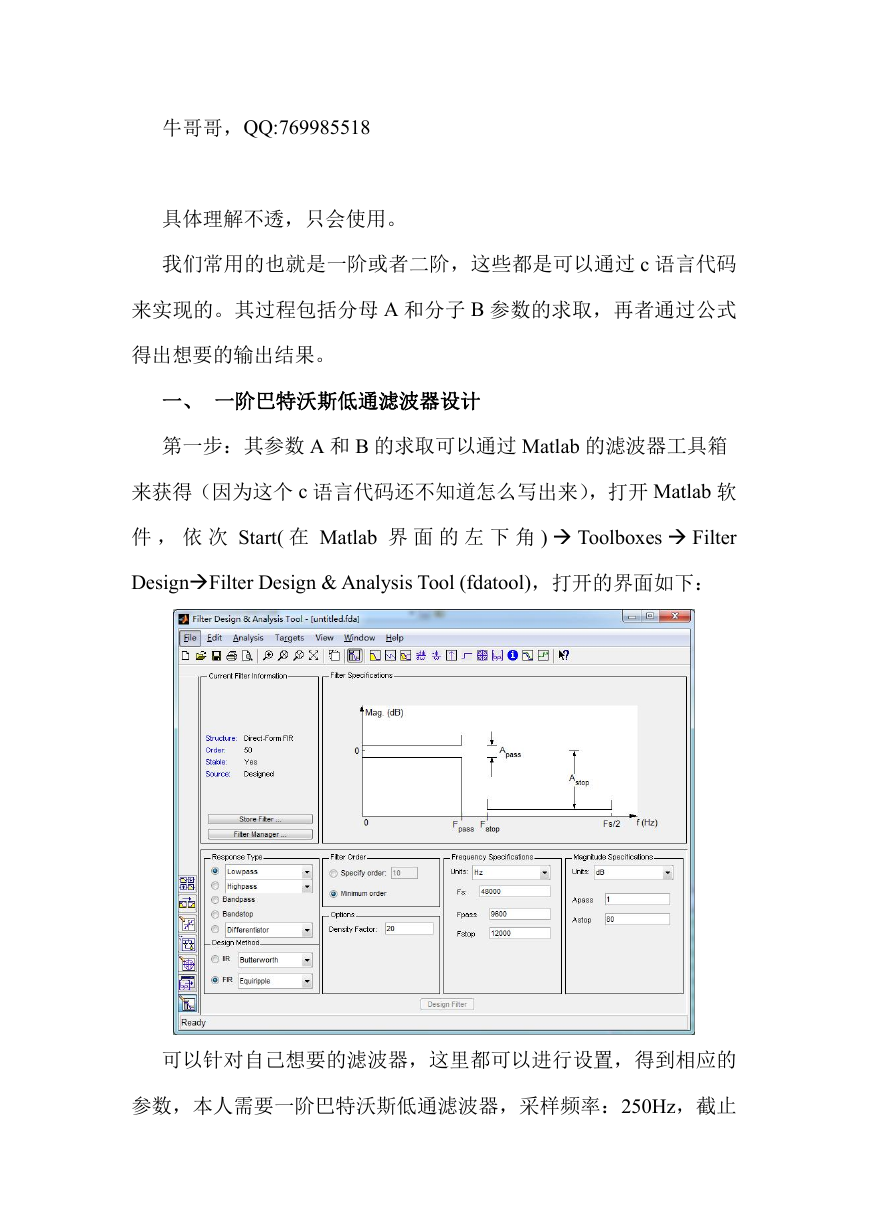
牛哥哥，QQ:769985518 具体理解不透，只会使用。 我们常用的也就是一阶或者二阶，这些都是可以通过 c 语言代码 来实现的。其过程包括分母 A 和分子 B 参数的求取，再者通过公式 得出想要的输出结果。 一、 一阶巴特沃斯低通滤波器设计 第一步：其参数 A 和 B 的求取可以通过 Matlab 的滤波器工具箱 来获得（因为这个 c 语言代码还不知道怎么写出来），打开 Matlab 软 件 ， 依 次 Start( 在 Matlab 界 面 的 左 下 角 )  Toolboxes  Filter DesignFilter Design & Analysis Tool (fdatool)，打开的界面如下： 可以针对自己想要的滤波器，这里都可以进行设置，得到相应的 参数，本人需要一阶巴特沃斯低通滤波器，采样频率：250Hz，截止 

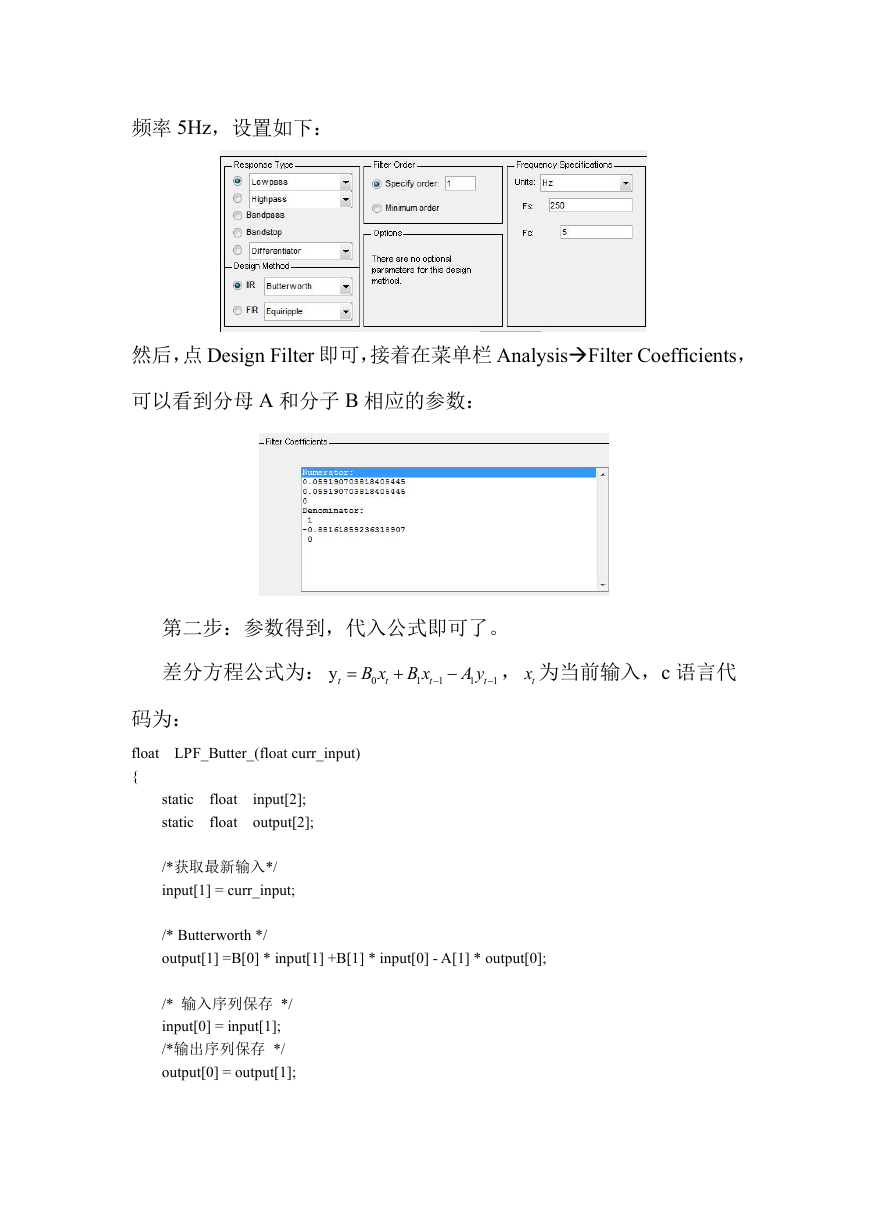
频率 5Hz，设置如下： 然后，点 Design Filter 即可，接着在菜单栏 AnalysisFilter Coefficients， 可以看到分母 A 和分子 B 相应的参数： 第二步：参数得到，代入公式即可了。 B x B x 0 1 t  t  A y 1 t 1  1  ， tx 为当前输入，c 语言代 差分方程公式为： yt  码为： float LPF_Butter_(float curr_input) { static static float float input[2]; output[2]; /*获取最新输入*/ input[1] = curr_input; /* Butterworth */ output[1] =B[0] * input[1] +B[1] * input[0] - A[1] * output[0]; /* 输入序列保存 */ input[0] = input[1]; /*输出序列保存 */ output[0] = output[1]; 

return output[1]; } 二、 二阶巴特沃斯低通滤波器设计 第一步：二阶的话，其用 Matlab 获取参数和 c 语言代码得到参数 都可以，Matlab 获取参数跟上述类似，现在使用 c 语言代码得到分子 B 和分母 A 的参数。 设置采样频率为 fs，截止频率为 fc，则： 代码为： /************************************************** 通过此函数可以得到二阶巴特沃斯的系数 ****************************************************/ void LPF2pSetCutoffFreq(float sample_freq, float cutoff_freq) { float fr =0; float ohm =0; float c =0; fr= sample_freq/cutoff_freq; ohm=tanf(M_PI_F/fr); c=1.0f+2.0f*cosf(M_PI_F/4.0f)*ohm + ohm*ohm; 

_cutoff_freq1 = cutoff_freq; if (_cutoff_freq1 > 0.0f) { } b_acc[0] = ohm*ohm/c; b_acc[1] = 2.0f*b_acc[0]; b_acc[2] = b_acc[0]; a_acc[1] = 2.0f*(ohm*ohm-1.0f)/c; a_acc[2] = (1.0f-2.0f*cosf(M_PI_F/4.0f)*ohm+ohm*ohm)/c; // // // // } 第二步：代入公式 一个二阶结构是这样的一个表达式： 这个表达式中需要过去的 4 个历史值： 1 x t  , x , y t , y t  ， 2 1  x  2 float LPF_Butter_(float curr_input) { static static float float input[3]; output[3]; /*获取最新输入*/ input[2] = curr_input; /* Butterworth */ output[2] =B[0] * input[2] +B[1] * input[1] +B[2] * input[0] - A[1] * output[1] - A[2] * output[0]; /* 输入序列保存 */ input[0] = input[1]; input[1] = input[2]; /*输出序列保存 */ output[0] = output[1]; output[1] = output[2]; return output[2]; } 有一个简单的技巧，可以把上面的计算简化，使得历史状态由 4 减为 2，定义下面的表达式： 

那么代码就可以写为： /****************************************** 二阶巴特沃斯低通滤波函数 *******************************************/ static float static float _delay_element_11; _delay_element_21; float LPF2pApply_1(float sample) { // buffered sample -1 // buffered sample -2 float delay_element_0 = 0, output=0; delay_element_0 = sample - _delay_element_11 * a_acc[1] - _delay_element_21 * a_acc[2]; if (isnan(delay_element_0) || isinf(delay_element_0)) { // don't allow bad values to propogate via the filter delay_element_0 = sample; } output = delay_element_0 * b_acc[0] + _delay_element_11 * b_acc[1] + _delay_element_21 * b_acc[2]; _delay_element_21 = _delay_element_11; _delay_element_11 = delay_element_0; // return the value. Should be no need to check limits return output; } // } 两种方法都可使用。，看个人选择