TSP 问题遗传算法通用 Matlab 程序（附图）(2007-03-10 09:56:14) 程序一：主程序 %TSP 问题（又名：旅行商问题，货郎担问题）遗传算法通用 matlab 程序 %D 是距离矩阵，n 为种群个数 %参数 a 是中国 31 个城市的坐标 %C 为停止代数，遗传到第 C 代时程序停止,C 的具体取值视问题的规模和耗费的时间而定 %m 为适应值归一化淘汰加速指数,最好取为 1,2,3,4,不宜太大 %alpha 为淘汰保护指数,可取为 0~1 之间任意小数,取 1 时关闭保护功能,建议取 0.8~1.0 之间的值 %R 为最短路径,Rlength 为路径长度 function [R,Rlength]=geneticTSP(D,a,n,C,m,alpha) a=[1304 2312;3639 1315;4177 2244;3712 1399;3488 1535;3326 1556;3238 1229;4196 1004; 4312 790;4386 570;3007 1970;2562 1756;2788 1491;2381 1676;1332 3918 2179;4061 2370;3780 2212;3676 2578;4029 2838;4263 2931;3429 3394 2643;3439 3201;2935 3240;3140 3550;2545 2357;2778 2826;2370 695;3715 1678; 1908;3507 2367; 2975]; [N,NN]=size(D); farm=zeros(n,N);%用于存储种群 for i=1:n farm(i,:)=randperm(N);%随机生成初始种群 end R=farm(1,:); 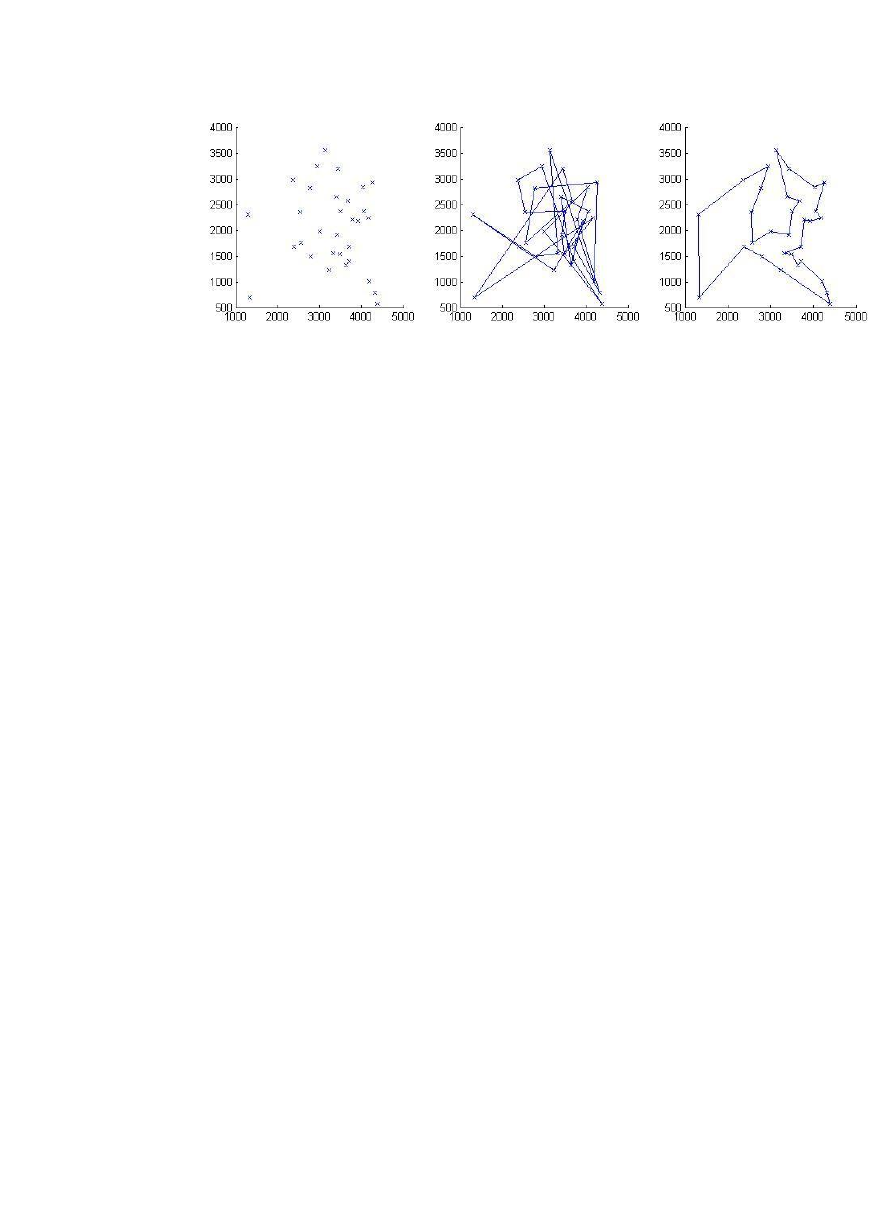subplot(1,3,1) scatter(a(:,1),a(:,2),'x') pause(1) subplot(1,3,2) plotaiwa(a,R) pause(1) farm(1,:)=R; len=zeros(n,1);%存储路径长度 fitness=zeros(n,1);%存储归一化适应值 counter=0; while counter for i=1:n 

len(i,1)=myLength(D,farm(i,:));%计算路径长度 end maxlen=max(len); minlen=min(len); fitness=fit(len,m,maxlen,minlen);%计算归一化适应值 rr=find(len==minlen); R=farm(rr(1,1),:);%更新最短路径 FARM=farm;%优胜劣汰，nn 记录了复制的个数 nn=0; for i=1:n if fitness(i,1)>=alpha*rand nn=nn+1; FARM(nn,:)=farm(i,:); end end FARM=FARM(1:nn,:); [aa,bb]=size(FARM);%交叉和变异 while aa if nn<=2 nnper=randperm(2); else nnper=randperm(nn); end A=FARM(nnper(1),:); B=FARM(nnper(2),:); [A,B]=intercross(A,B); FARM=[FARM;A;B]; [aa,bb]=size(FARM); end if aa>n FARM=FARM(1:n,:);%保持种群规模为 n end farm=FARM; clear FARM counter=counter+1 end Rlength=myLength(D,R); 

subplot(1,3,3) plotaiwa(a,R) 程序二：计算邻接矩阵 %输入参数 a 是中国 31 个城市的坐标 %输出参数 D 是无向图的赋权邻接矩阵 function D=ff01(a) [c,d]=size(a); D=zeros(c,c); for i=1:c for j=i:c bb=(a(i,1)-a(j,1)).^2+(a(i,2)-a(j,2)).^2; D(i,j)=bb^(0.5); D(j,i)=D(i,j); end end 程序三：计算归一化适应值 %计算归一化适应值的子程序 function fitness=fit(len,m,maxlen,minlen) fitness=len; for i=1:length(len) fitness(i,1)=(1-((len(i,1)-minlen)/(maxlen-minlen+0.0001))).^m; end 程序四：交叉和变异的子程序 %交叉算法采用的是由 Goldberg 和 Lingle 于 1985 年提出的 PMX(部分匹配交叉) function [a,b]=intercross(a,b) L=length(a); if L<=10%确定交叉宽度 W=9; elseif ((L/10)-floor(L/10))>=rand&&L>10 W=ceil(L/10)+8; else W=floor(L/10)+8; end p=unidrnd(L-W+1);%随机选择交叉范围，从 p 到 p+W for i=1:W%交叉 x=find(a==b(1,p+i-1)); 

y=find(b==a(1,p+i-1)); [a(1,p+i-1),b(1,p+i-1)]=exchange(a(1,p+i-1),b(1,p+i-1)); [a(1,x),b(1,y)]=exchange(a(1,x),b(1,y)); end function [x,y]=exchange(x,y) temp=x; x=y; y=temp; 程序五: 计算路径的子程序 %该路径长度是一个闭合的路径的长度 function len=myLength(D,p) [N,NN]=size(D); len=D(p(1,N),p(1,1)); for i=1:(N-1) len=len+D(p(1,i),p(1,i+1)); end 程序六：用于绘制路径示意图的程序 function plotaiwa(a,R) scatter(a(:,1),a(:,2),'x') hold on plot([a(R(1),1),a(R(31),1)],[a(R(1),2),a(R(31),2)]) hold on for i=2:length(R) x0=a(R(i-1),1); y0=a(R(i-1),2); x1=a(R(i),1); y1=a(R(i),2); xx=[x0,x1]; yy=[y0,y1]; plot(xx,yy) hold on end