60 2018，54（1） Computer Engineering and Applications 计算机工程与应用 融合空时相干和特征空间波束形成的超声成像 孟德明 1，2，3，陈 昕 1，2，和小念 1，2，陈思平 1，2 MENG Deming1，2，3, CHEN Xin1，2, HE Xiaonian1，2, CHEN Siping1，2 1. 深圳大学 生物医学工程学院，广东 深圳 518060 2. 医学超声关键技术国家地方联合工程实验室，广东 深圳 518060 3. 桂林电子科技大学，广西 桂林 541004 1.School of Biomedical Engineering, Shenzhen University, Shenzhen, Guandong 518060, China 2.National-Regional Key Technology Engineering Laboratory for Medical Ultrasound, Shenzhen, Guandong 518060, China 3.Guilin University of Electronic Technology, Guilin, Guangxi 541004, China MENG Deming, CHEN Xin, HE Xiaonian, et al. Eigenspace-based beamforming combined with spatio-temporally coherence factor for ultrasound imaging. Computer Engineering and Applications, 2018, 54（1）：60-63. Abstract：To improve the quality of medical ultrasound imaging, a beamforming method which combines Eigen Space- Based Minimum Variance（ESBMV）with Spatio- Temporally Coherence Factor（STCF）is proposed. Firstly, minimum variance beamforming is used to obtain covariance matrix and weight vector; then the weight vector of the ESBMV is found by projecting the MV weight vector onto a vector subspace constructed from the eigenstructure of the covariance matrix; at the same time, the spatio-temporally method is used to calculate the coherence factor; in the end, the spatio- temporally coherence factor is used to optimize the results of eigenspace-based minimum variance beamforming. Simula- tions of point scatters and cyst phantom are used to verify the proposed method. The results show that the proposed method provides improved contrast, better speckle performance and more robustness than the ESBMV and ESBMV-CF beam- forming method, at the expense of slightly lower resolution. Key words：ultrasound imaging; adaptive beamforming; minimum variance; eigenspace; Spatio-Temporally Coherence Factor（STCF） 摘 要：为了进一步提高超声成像的质量，提出了融合特征空间最小波束形成和空时相干系数的成像方法。首先利 用最小方差法计算回波数据的协方差矩阵和加权向量 ；然后对协方差矩阵进行特征分解得到信号子空间，并将加权 向量投影到信号子空间，得到特征空间方法的加权向量 ；同时采用空时平滑方法计算相干系数，最后用空时相干系 数作为加权系数对特征空间最小方差波束形成的结果进行优化。为了验证算法的有效性，对医学成像上常用的点 目标和斑目标进行了成像，仿真实验结果表明 ：与特征空间最小方差算法和融合特征空间与相干系数的算法相比， 提出的方法提高了对比度和稳健性，其代价是略微降低了成像分辨率。 关键词：超声成像 ；自适应波束形成 ；最小方差 ；特征空间 ；空时相干系数 文献标志码：A 中图分类号：TP391 doi：10.3778/j.issn.1002-8331.1611-0007 1 引言 在医学超声成像中，延时叠加（Delay-and-Sum，DAS） 波束形成方法未考虑回波信号特性，导致成像空间分辨 率 较 低 ，对 比 度 较 差 [1- 2]。 自 适 应 最 小 方 差（Minimum Variance，MV）波束形成算法根据回波信号的特征计算 各通道加权值，达到了压缩波束主瓣宽度，提高图像分 辨率的目的[3]。由于医学超声信号的高相关性、宽带等 特点[4]，在 MV 算法中，协方差矩阵计算时会出现奇异矩 阵的现象。Synnevåg[5]等采用了空间平滑技术，解相关 回波信号，获得更精确的协方差矩阵的估计；Asl[6]等采 基金项目：国家自然科学基金（No.61372006）。 作者简介：孟德明（1977—），男，博士，主要研究领域为医学超声信号处理，E-mail：mengdeming@guet.edu.cn。 收稿日期：2016-11-01 修回日期：2017-03-28 文章编号：1002-8331（2018）01-0060-04 计算机工程与应用www.ceaj.org

孟德明，陈 昕，和小念，等：融合空时相干和特征空间波束形成的超声成像 2018，54（1） 61 用前后向空间平滑法去除了回波信号的相关性；Li[7]等提 出了对角加载方法，通过获得稳健的协方差矩阵来提高 MV 算法的鲁棒性。Mohammadzadeh[8]等提出了特征空 间最小方差波束形算法（Eigen Space-Based MV，ESBMV）， 进一步去除了噪声和干扰信号对成像结果的影响，获得 了高对比度和高分辨率的医学超声图像。 文献[9]和[10]中提出用相干系数 CF（Coherence Fac- tor）评价成像质量方法。Li[11]等扩展了相干系数的概念， 提出一种广义相干系数，以略微降低了成像分辨率为代 价，提高了成像的稳健性。Xu[12]提出空时平滑相干系 数，改善了亮斑目标成像时的黑区伪像问题。Asl[13]等 将相干系数引入到最小方差波束形成算法中，利用相干 系数弥补了 MV 算法对比度不高的缺点，提高了超声成 像对比度。Wang[14]提出了一种基于最小方差的相干系 数，并应用于平面波成像中，提高了成像对比度。吴文 焘[15]等将广义相干系数引入到最小方差波束形成算法 中，提高了成像的对比度，增强了算法对相位误差的鲁 棒性。Zeng[16]等将相干系数引入到特征空间最小方差 波束形成算法中，进一步提高了超声成像的分辨率。 Zhao[17]等提出了一种子阵相干系数，并引入到特征空间 最小方差波束形成算法中，以较小的计算量提升为代价 提高了成像的对比度和分辨率。 本文提出一种融合特征空间最小方差波束形成与 空时相干系数的超声成像算法，该算法利用空时平滑方 法计算相干系数，减少相干系数值的扰动，优化相干系 数的计算。为验证本文所提方法的有效性，将本文算法 分别与 DAS、MV、ESBMV、ESBMV_CF 算法进行了比 较分析。 2 算法 2.1 信号模型和最小方差波束形成 假设一个由 M 个等间距的阵元组成的线性换能 器，接收了近场内散射目标的反射信号，则波束形成的 输出可表示为： y(k) = wH(k)xd(k) = ∑ M i = 1 wi(k)xi(k - Δi) （1） 其 中 k 表 示 时 间 系 数 ，xd(k) =[x1(k - Δ1),x2(k - Δ2),…, xM(k - ΔM)]T为聚焦延时后的信号，w(k) =[w1(1),w2(2),…, wM(M)]T 为加权向量，Δi 为各通道延时。当 w(k) 为全 1 向量时，波束形成方法退化为传统 DAS 算法。 最小方差波束形成算法的基本思想是在期望信号 增益不变的情况下，通过使阵列的输出能量最小化的方 法，寻找最优的加权向量 w ，其数学表达式为[7]： min w wH Ri + nw subject to wHa = 1 （2） STCF(k) = 其中，Ri + n 是干扰加噪声的协方差矩阵，a 为方向向 量，经过延时聚焦后，a 表示为 a =[1,1,…,1] ，由此可得 K ∑ n = - K | || ∑ M - L ∑ | m = l l = 0 L + l - 1xm(k,n) 2 | || | (M - L + 1) ∑ K ∑ M - L n = - K l = 0 | || ∑ L + l - 1xm(k,n) | m = l 2 | || | （10） 加权矢量为： -1a wMV = Ri + n -1a aH Ri + n 在实际中应用中，用回波信号的采样协方差矩阵 R͂ 取代式（3）中的协方差矩阵。为了去除回波信号的相关 性，利用空间平滑方法重构采样协方差矩阵： （3） R͂ = M - L + 1 1 M - L + 1 ∑ l = 1 d(k),xl + 1 d(k) =[xl d 其中 x l 输出向量，则空间平滑后的输出为： (k),…,xl + L - 1 d d(k)x l x l d(k)H （4） (k)]T 为第 l 个子阵的 y(k) = M - L + 1 1 M - L + 1 ∑ l = 1 wH MV(k)x l d(k) （5） 2.2 特征空间最小方差波束形成 在特征空间波束形成（ESBMV）方法中，将协方差 矩分解为信号子空间和噪声子空间，然后将由 MV 算法 中加权向量 wmv 投影到信号子空间中[3]，进一步降了低 旁瓣信号幅度。协方差矩阵的特征分解可以表示为： s + En Λn E H n R(k) = Es Λs E H （6） 设 λi 为 特 征 值 ，将 R(k) 的 特 征 值 由 大 到 小 排 列 λ1 > λ2 > …λi⋯ > λM 。 则 Λs = diag(λ1,λ2,…,λnum) 对 应 特征向量为 Es 和 Λn = diag(λnum,λnum + 1,…,λM) 对应特 征向量为 En 。 Es 和 En 分别对应信号子空间和噪声 子空间，num 为信号子空间的维数，num 的大小决定了 特征值分解方法保持主瓣和压低旁瓣信号的能力，通 常用大于最大特征值 α 倍特征向量个数决定，其中 α 取 值范围为 0.1～0.5。将 wmv 投影到信号子空间，得到 ESBMV 的加权向量为： s wMV wESBMV = Es E H （7） 由此得到的 ESBMV 波束形成的最终输出： y(k) = M - L + 1 1 M - L + 1 ∑ l = 1 wH ESBMV(k)x l d(k) （8） 2.3 空时平滑相干系数 相干系数反映了回波信号的相干程度，其定义可以 表示为： CF(k) = | || ∑ M - 1xm(k) | M ∑ 2 | || | | | xm(k) 2 m = 0 M - 1 m = 0 （9） CF 是用信号幅度分布来表示的，由于回波信号的 随机性，为了降低 CF 值的变化对最终成像的影响，利 用空时平滑方法修正相干系数[12]，空时平滑的相干系数 表示为： 计算机工程与应用www.ceaj.org

62 2018，54（1） Computer Engineering and Applications 计算机工程与应用 式中，M 为阵列的阵元数，L 为子阵的长度，K 为深度 方向的采样点数，一般设置为 2 个波长的采样点数（与 发射脉冲长度一致）；空时平滑的方法降低相干因子的 扰动，优化了相干系数的计算。 2.4 ESBMV-STCF 算法 特征空间的最小方差波束形成与空时相干系数融 合（ESBMV-STCF）的超声成像算法流程如图 1 所示，首 先采用 ESBMV 算法对回波信号进行波束形成处理，同 时计算 STCF 系数，最后采用 STCF 系数对 ESBMV 波束 形成结果进行加权成像。 换能器阵列 回波信号 延时聚焦 ESBMV 波束形 STCF 估计 成 像 图 1 ESBMV-STCF 成像算法流程 对于成像点，根据式（8）、（10），可得 ESBMV-STCF 波束形成的最终输出为： 1 y(k) = STCF(k) M - L + 1 M - L + 1 ∑ l = 1 wH ESBMV(k)x l d(k) 35 40 45 50 55 60 65 70 / m m 离 距 向 轴 35 40 45 50 55 60 65 70 / m m 离 距 向 轴 35 40 45 50 55 60 65 70 / m m 离 距 向 轴 75 0 -5 5 横向距离/mm （a）DAS 35 75 0 -5 5 横向距离/mm （b）MV 75 0 -5 5 横向距离/mm （c）ESBMV 40 45 50 55 60 65 70 / m m 离 距 向 轴 0 75 -5 5 横向距离/mm （d）ESBMV-CF 35 40 45 50 55 60 65 70 / m m 离 距 向 轴 75 0 -5 5 横向距离/mm （e）ESBMV-STCF 3 仿真结果及讨论 为了研究本文所述算法的性能，利用 Field II 进行 点射目标和斑散射目标的仿真实验。采用 M = 96 阵元 线阵换能器，阵元间距为半个波长，设置中心频率 f0 为 4 MHz，采样频率 fs 为 100 MHz，声速为 1 540 m/s，子阵 长度 L 为 M 2 。所有仿真均采用定点聚焦发射和动态 接收聚焦的工作模式，仿真成像分别对点散射目标和斑 目标进行成像。采用 DAS 算法、MV 算法、ESBMV 算 法、ESBMV-CF 算法和 ESBMV-STCF 算法成像并对比， 对接收回波信号加入了 60 dB 的高斯白噪声。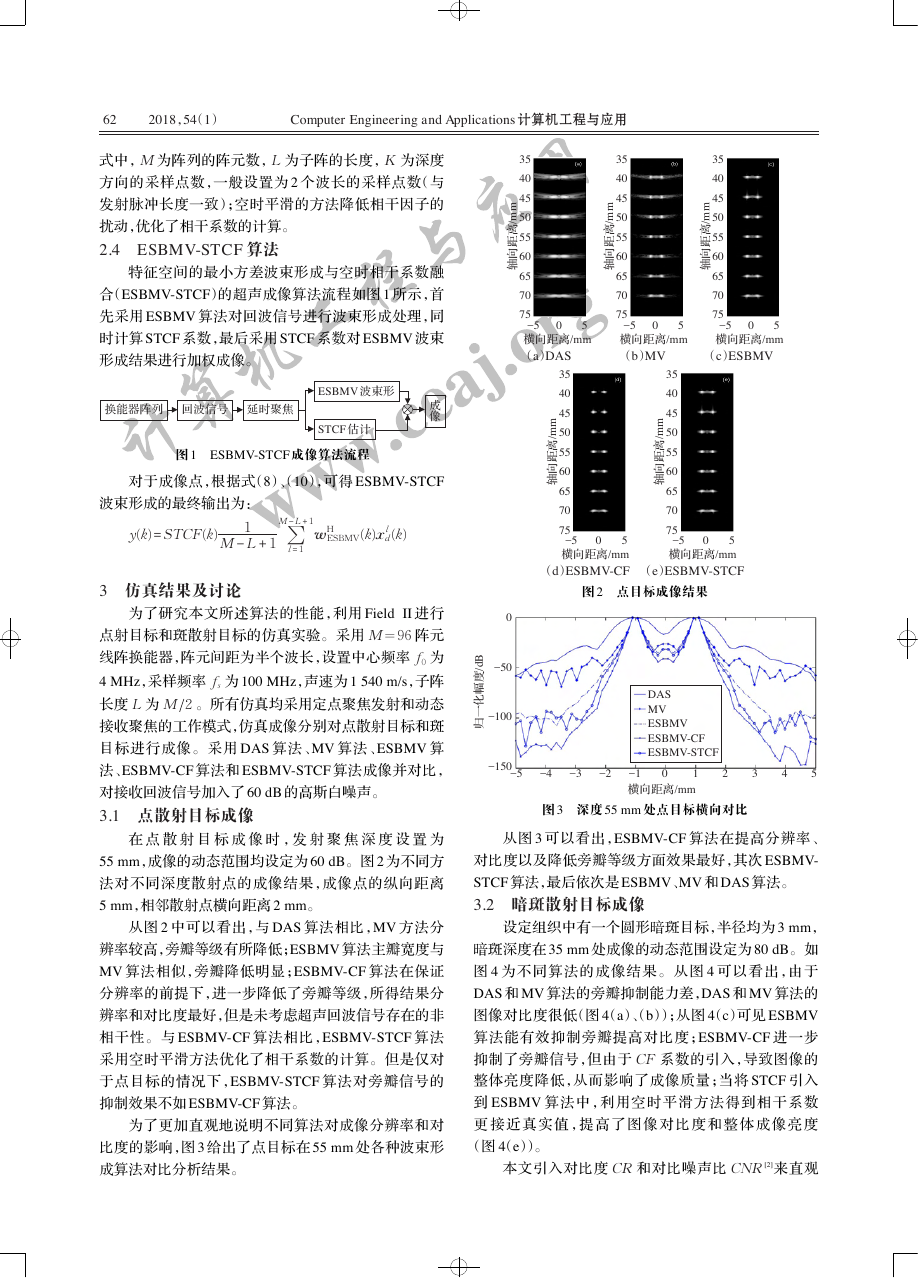 3.1 点散射目标成像 在 点 散 射 目 标 成 像 时 ，发 射 聚 焦 深 度 设 置 为 55 mm，成像的动态范围均设定为 60 dB。图 2 为不同方 法对不同深度散射点的成像结果，成像点的纵向距离 5 mm，相邻散射点横向距离 2 mm。 从图 2 中可以看出，与 DAS 算法相比，MV 方法分 辨率较高，旁瓣等级有所降低；ESBMV 算法主瓣宽度与 MV 算法相似，旁瓣降低明显；ESBMV-CF 算法在保证 分辨率的前提下，进一步降低了旁瓣等级，所得结果分 辨率和对比度最好，但是未考虑超声回波信号存在的非 相干性。与 ESBMV-CF 算法相比，ESBMV-STCF 算法 采用空时平滑方法优化了相干系数的计算。但是仅对 于点目标的情况下，ESBMV-STCF 算法对旁瓣信号的 抑制效果不如 ESBMV-CF 算法。 为了更加直观地说明不同算法对成像分辨率和对 比度的影响，图 3 给出了点目标在 55 mm 处各种波束形 成算法对比分析结果。 0 -50 -100 B d / 度 幅 化 一 归 图 2 点目标成像结果 DAS MV ESBMV ESBMV-CF ESBMV-STCF -150 -5 -4 -3 -2 0 -1 1 横向距离/mm 2 3 4 5 图 3 深度 55 mm 处点目标横向对比 从图 3 可以看出，ESBMV-CF 算法在提高分辨率、 对比度以及降低旁瓣等级方面效果最好，其次 ESBMV- STCF 算法，最后依次是 ESBMV、MV 和 DAS 算法。 3.2 暗斑散射目标成像 设定组织中有一个圆形暗斑目标，半径均为 3 mm， 暗斑深度在 35 mm 处成像的动态范围设定为 80 dB。如 图 4 为不同算法的成像结果。从图 4 可以看出，由于 DAS 和 MV 算法的旁瓣抑制能力差，DAS 和 MV 算法的 图像对比度很低（图 4（a）、（b））；从图 4（c）可见 ESBMV 算法能有效抑制旁瓣提高对比度；ESBMV-CF 进一步 抑制了旁瓣信号，但由于 CF 系数的引入，导致图像的 整体亮度降低，从而影响了成像质量；当将 STCF 引入 到 ESBMV 算法中，利用空时平滑方法得到相干系数 更 接 近 真 实 值 ，提 高 了 图 像 对 比 度 和 整 体 成 像 亮 度 （图 4（e））。 本文引入对比度 CR 和对比噪声比 CNR [2]来直观 计算机工程与应用www.ceaj.org

孟德明，陈 昕，和小念，等：融合空时相干和特征空间波束形成的超声成像 2018，54（1） 63 30 35 40 / m m 离 距 向 纵 30 35 40 / m m 离 距 向 纵 0 -5 5 横向距离/mm （a）DAS 0 -5 5 横向距离/mm （a）DAS 30 35 40 / m m 离 距 向 纵 30 35 40 / m m 离 距 向 纵 / m m 离 距 向 纵 30 35 40 0 -5 5 横向距离/mm （c）ESBMV / m m 离 距 向 纵 30 35 40 0 -5 5 横向距离/mm （d）ESBMV-CF 0 -5 5 横向距离/mm （b）MV 图 4 暗斑散射目标仿真成像结果 / m m 离 距 向 纵 30 35 40 0 -5 5 横向距离/mm （c）ESBMV / m m 离 距 向 纵 30 35 40 0 -5 5 横向距离/mm （d）ESBMV-CF 0 -5 5 横向距离/mm （b）MV 图 5 亮斑散射目标仿真成像结果 30 35 40 / m m 离 距 向 纵 0 -5 5 横向距离/mm （e）ESBMV-STCF 30 35 40 / m m 离 距 向 纵 0 -5 5 横向距离/mm （e）ESBMV-STCF 地评价不同波束形成方法的对比分辨率，其中对比度 CR 定义为中心区域的平均功率与背景区域的平均功率 之差，对比噪声比 CNR 定义为 CR 除以背景区域的方 差。表１列出各种波束形成方法的对比度。 表 1 斑散射目标对比度与对比噪声比 波束形成算法 DAS MV ESBMV ESBMV-CF ESBMV-STCF 中心平均 背景平均 对比度 功率 -41.65 -52.18 -60.23 -72.60 -71.24 功率 -12.98 -17.45 -17.95 -24.61 -21.54 CR 28.67 34.73 42.28 47.99 49.70 dB 对比噪声比 CNR 4.49 4.56 5.19 3.52 6.15 从表 1 可以看出，ESBMV-STCF 算法的 CR 和 CNR 均优于其他算法。ESBMV 类算法中心平均功率明显小 于 DAS 和 MV 算法，ESBMV-CF 算法中相干系数计算时 未考虑到超声回波信号非相干性，抑制了非相干信号， 因此 ESBMV-CF 算法中心平均功率最小，但背景平均功 率下将更显著；ESBMV-STCF 算法优化了相干系数的 计算，使得到的相干系数更接近真实值，因此对比度和 对比噪声比优于 ESBMV-CF 算法。 3.3 亮斑散射目标成像 设定组织中有一个圆形亮斑目标，半径均为 3 mm， 暗斑深度在 35 mm 处成像的动态范围设定为 80 dB。如 图 5 为不同算法的成像结果。 从图 5 可以看出，对于亮斑成像目标，由于 DAS 算 法的旁瓣抑制能力差，旁瓣信号扩散到亮斑附近区域， ESBMV 和 ESBMV-CF 算法（图 4（c）、（d））在亮斑目标 附件产生了明显的黑区伪影，降低了整体成像质量；与 ESBMV 和 ESBMV-CF 算法相比，ESBMV-STCF 算法优 化了相干系数的计算，使得到的相干系数更接近真实 值，较好地抑制了亮斑附近区域的黑区伪影，提高了成 像质量。 4 结论 本文提出一种特征空间与空时平滑相干系数融合 的波束形成算法。该算法在保证特征空间法成像分辨 率基础上，利用了空时平滑相干系数作为校正量提升了 算法稳定性和成像对比度。通过对点散射目标以及斑 散射目标的成像实验，对分辨率、对比度、对比噪声比进 行比较。特征空间最小方差波束形成只能针对点散射 目标成像获得高分辨以及高对比度，而对于复杂的斑散 射目标成像，本文提出的方法提高了成像对比度、对比 噪声比，特别是对于亮斑目标，本文提出的算法能够有 效抑制黑区伪影。因此，ESBMV-STCF 算法是一种更 为有效的波束形成算法。 参考文献： [1] 郑驰超，彭虎 . 基于编码发射与自适应波束形成的超声成 像[J]. 电子与信息学报，2010，32（4）：959-962. [2] 王平，许琴，范文政，等 . 超声成像中基于特征空间的前后 向最小方差波束形成[J]. 声学学报，2013，38（1）：65-70. [3] 刘婷婷，周浩，郑音飞 . 特征空间和符号相干系数融合的最 小方差超声波束形成[J]. 声学学报，2015（6）：855-862. [4] 刘昊霖，易宗锐，刘东权 . 相干系数与幅度相位估计融合的 医学超声成像算法[J]. 四川大学学报：工程科学版，2015 （S2）：125-129. [5] Synnevåg J F，Austeng A，Holm S.Adaptive beamforming applied to medical ultrasound imaging[J].IEEE Transactions on Ultrasonics，Ferroelectrics，and Frequency Control， 2007，54（8）：1606-1613. [6] Asl B M，Mahloojifar A.Contrast enhancement and robust- ness improvement of adaptive ultrasound imaging using forward- backward minimum variance beamforming[J]. IEEE Transactions on Ultrasonics，Ferroelectrics，and Frequency Control，2011，58（4）：858-867. （下转 85 页） 计算机工程与应用www.ceaj.org