Computer Engineering and Applications 计算机工程与应用 2018，54（5） 91 基于混沌映射和 DNA 编码的图像加密算法 施 飞，张红梅，张向利 SHI Fei, ZHANG Hongmei, ZHANG Xiangli 桂林电子科技大学 广西高校云计算与复杂系统重点实验室，广西 桂林 541004 Guangxi Colleges and Universities Key Laboratory of Cloud Computing and Complex Systems, Guilin University of Elec- tronic Technology, Guilin, Guangxi 541004, China SHI Fei, ZHANG Hongmei, ZHANG Xiangli. Image encryption algorithm based on chaotic map and DNA coding. Computer Engineering and Applications, 2018, 54（5）：91-95. Abstract：In order to improve the efficiency and security of image encryption, an image encryption algorithm based on chaotic map and DNA sequence is proposed, which is based on the analysis of the existing image encryption algorithms. First of all, adopting the chaotic mapping to generate chaos sequence of image scrambling in bit-plane and to achieve the dual effect of encryption, image scrambling and diffusion. Then using the DNA encoding rules to code after scrambling image with DNA computing and to realize the diffusion of the image. The experimental results indicate that the key space of the proposed algorithm is large enough, the key sensitivity is strong, and it has better security. Key words：chaotic map; image encryption; bit-plane; DNA coding; scrambling and diffusion 摘 要：为了有效改进图像的加密效果及安全性，在对已有的图像加密算法进行分析的基础上，提出基于混沌映射 的位变换和 DNA 序列的图像加密算法。首先，采用混沌映射生成置乱序列对图像在位平面进行置乱，同时达到了 图像置乱和扩散的双重加密效果。然后，利用 DNA 编码规则，对置乱后的图像编码，进行 DNA 运算，实现图像的扩 散。实验结果表明，该算法密钥空间足够大，密钥敏感性较强，具有较好的安全性。 关键词：混沌映射 ；图像加密 ；位平面 ；DNA 运算 ；置乱扩散 文献标志码：A 中图分类号：TP301.6 doi：10.3778/j.issn.1002-8331.1610-0208 1 引言 随着网络和多媒体技术的快速发展和普及，人们的 网络活动日益频繁，信息安全问题日益突出，其中图像 等多媒体数据的安全问题也日益引起人们的关注。由 于数字图像不同于文本信息，具有数据量大、冗余度高、 相关性强等特点，因此采用传统的加密方式无法对图像 进行有效的加密。 混沌系统的类随机性、对初值敏感性、非周期性、非 收敛性以及难以预测等属性使得混沌与密码学有着天 然的联系，使得混沌非常适用于图像加密。混沌系统的 这些特点使其广泛地被应用于数据加密中[1-5]。目前，基 于混沌的图像加密主要包括基于置乱的加密技术、基于 灰度替换的加密技术以及基于混合迭代结构的图像加 密技术[6-8]。文献[9]提出了基于一次一密及强混沌映射 的流密码算法，该算法利用分段线性混沌序列作为伪随 机密钥流序列的生成器，将混沌算法和传统的循环加密 结合，具有强健的抗噪声性能。 1994 年，Adleman 首次提出 DNA 计算[10]，为图像加 密领域开辟了新的研究方向。DNA 计算在运算速度、 节能、存储等方面有很优秀的特性，基于 DNA 计算的图 像加密获得了很好的发展[11]，并且学者们将混沌理论和 DNA 计算理论结合应用于数字图像加密领域，取得了 很好的加密效果。梁涛、李华利用混沌序列对图像和 DNA 编码后的图像序列进行两次置乱实现读图像的加 密。房东鑫、张健[12]将 DNA 计算与猫映射结合，提高了 猫映射用于图像置乱的安全强度。张健、房东鑫[13]利用 基金项目：国家自然科学基金（No.61461010，No.61363031）；广西高校云计算复杂系统重点实验室（研究课题 14101）。 作者简介：施飞（1989—），男，硕士生，主要研究领域：信息安全；张红梅（1970—），女，博士，教授，主要研究领域：信息安全、入侵 检测；张向利（1968—），女，博士，教授，主要研究领域：物联网技术、网络化监控系统。 收稿日期：2016-10-18 修回日期：2017-03-15 文章编号：1002-8331（2018）05-0091-05 CNKI 网络出版：2017-06-22, http://kns.cnki.net/kcms/detail/11.2127.TP.20170622.1850.016.html 计算机工程与应用www.ceaj.org

92 2018，54（5） Computer Engineering and Applications 计算机工程与应用 Chebyshev 映射和 DNA 编码对置乱后的图像进行扩散 加密，对灰度图像有很好的加密效果。文献[14]提出了 利用位平面置乱和高维混沌映射对彩色图像进行加 密。本文同样是在位平面对图像进行置乱加密，然后在 位平面加密的基础上对图像的二进制进行 DNA 编码， 进行 DNA 运算对图像进行加密。 本文研究了基于混沌映射、位运算和 DNA 编码的 图像加密算法[14-20]，在此基础上，利用混沌映射对图像在 位平面进行置乱，能使加密图像同时达到置乱和扩散的 效果，然后对置乱后图像进行 DNA 编码，进行 DNA 运 算，对图像进行混乱。理论分析实验结果表明：该算法 具有较好的加密效果和安全性。 编码的规则可以表示为 4 个核酸碱基。例如按表 1 中的 编码规则 1 用 A、T、C 和 G 分别表示 00、11、10 和 01，对 像素灰度值 121 的点，二进制序列表示为[01111001]，对 应的 DNA 序列表示为[CTGC]。 随着 DNA 计算的快速发展，基于 DNA 序列的生物 操作和代数操作已经出现，DNA 异或、DNA 加法、DNA 减法和求 DNA 的互补序列等操作与传统的二进制操作 相 类 似 。 与 8 种 DNA 编 码 规 则 相 对 应 ，也 存 在 8 种 DNA 异或、DNA 加法和 DNA 减法规则。DNA 编码规 则 0、1 和 2 分别对应的 DNA 异或、DNA 加法和 DNA 减 法规则，见表 2、表 3 和表 4。 表 2 DNA 编码规则 0 对应 DNA 序列异或规则 2 算法基础 2.1 混沌系统 2.1.1 Logistic 映射 Logistic 映射模型是 1976 年生态学家 R.May 在研究 昆虫群体繁殖规律时提出的，因此人们习惯上也称其为 “虫口模型”。其数学定义为： xn + 1 = μxn(1 - xn) （1） 其 中 μ ∈(0,4) ，xn ∈(0,1) 。 当 3.569 945 6< μ ≤ 4 时 ， Logistic 映射处于混沌状态。 2.1.2 Kent 映射 Kent 映射数学定义为： xi + 1 = xi p, 0 < xi ≤ p 1 - xi 1 - p , p < xi ≤ 1 ì ïï í ïï î （2） 其中，p 为混沌系统的控制参数，并且当 xi ∈(0,1) ， p ∈(0,1) 时，Kent 映射处于混沌状态。 2.2 DNA 序列编码 DNA 序列是使用一串字母表示所携带的基因信息 的分子结构，字母的种类只有 A、C、G、T 四种，代表分子 里的四种核酸碱基，其中 A 与 T、C 与 G 互补配对。将图 像的每一个像素用 8 位二进制表示，每 2 位用一个 DNA 碱基表示，其中二进制中 0 和 1 是互补的，因此可以设定 00 和 11、01 和 10 互补，从而二进制编码与 DNA 编码产 生结构上和特性上的联系。由此可以得到 DNA 编码的 8 种规则，见表 1。 表 1 二进制对与 DNA 编码规则表 0 00 11 01 10 1 00 11 10 01 2 01 10 00 11 3 01 10 11 00 4 10 01 00 11 5 10 01 11 00 6 11 00 01 10 7 11 00 10 01 A T C G 像素是图像的基本构成单元，像素点灰度值在计算 机中以 8 位的二进制序列表示，按照二进制对与 DNA XOR A G C T A A G C T G G A T C C C T A G T T C G A 表 3 DNA 编码规则 1 对应 DNA 序列加法规则 + A G C T A A G C T G G C T A C C T A G T T A G C 表 4 DNA 编码规则 2 对应 DNA 序列减法规则 - C A T G C C G T A A A C G T T T A C G G G T A C 2.3 图像的二进制位平面分解 图像的每一个像素点的灰度值都可以转换成二进 制数，这样可以从二进制位的角度出发，将图片分解成 若干个位平面。在位平面对图像进行置乱，能够同时达 到置乱和扩散的效果，相较于在像素平面进行置乱，仅 仅能够达到像素位置置乱，像素值并没有改变的缺陷， 位平面的置乱，不仅改变了像素的位置，而且像素值也 改变了。 图像转换成二进制后，每一位的位置不同，权重不 同，包含的像素信息也就不同。高位的权重高，包含的 图像信息多；低位的权重低，包含的像素信息少。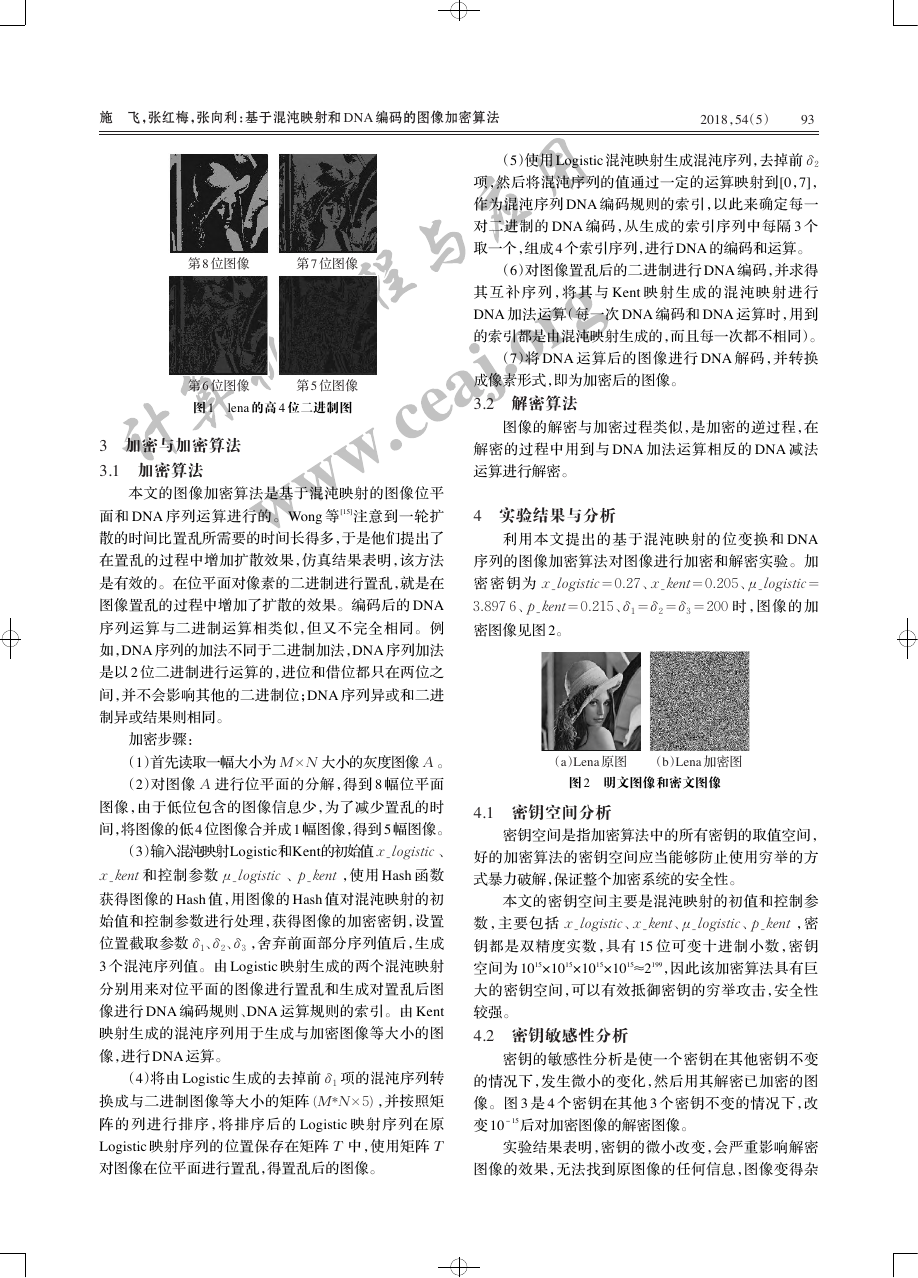将第 i 位二进制包含的像素信息占该像素的百分比表示为： p(i) = 2i ∑ 2i 7 t = 0 （3） 由公式知，图像的信息主要集中在高位，低位含有 的信息少。由图 1 看到，图像的第 5 位二进制图像就几 乎看不到图像的任何信息，由公式及图像进一步推理得 知：低位更看不到任何信息。 计算机工程与应用www.ceaj.org

施 飞，张红梅，张向利：基于混沌映射和 DNA 编码的图像加密算法 2018，54（5） 93 第 8 位图像 第 7 位图像 （5）使用 Logistic 混沌映射生成混沌序列，去掉前 δ2 项，然后将混沌序列的值通过一定的运算映射到[0，7]， 作为混沌序列 DNA 编码规则的索引，以此来确定每一 对二进制的 DNA 编码，从生成的索引序列中每隔 3 个 取一个，组成 4 个索引序列，进行 DNA 的编码和运算。 （6）对图像置乱后的二进制进行 DNA 编码，并求得 其 互 补 序 列 ，将 其 与 Kent 映 射 生 成 的 混 沌 映 射 进 行 DNA 加法运算（每一次 DNA 编码和 DNA 运算时，用到 的索引都是由混沌映射生成的，而且每一次都不相同）。 （7）将 DNA 运算后的图像进行 DNA 解码，并转换 第 6 位图像 图 1 第 5 位图像 lena 的高 4 位二进制图 成像素形式，即为加密后的图像。 3.2 解密算法 3 加密与加密算法 3.1 加密算法 本文的图像加密算法是基于混沌映射的图像位平 面和 DNA 序列运算进行的。Wong 等 [15]注意到一轮扩 散的时间比置乱所需要的时间长得多，于是他们提出了 在置乱的过程中增加扩散效果，仿真结果表明，该方法 是有效的。在位平面对像素的二进制进行置乱，就是在 图像置乱的过程中增加了扩散的效果。编码后的 DNA 序列运算与二进制运算相类似，但又不完全相同。例 如，DNA 序列的加法不同于二进制加法，DNA 序列加法 是以 2 位二进制进行运算的，进位和借位都只在两位之 间，并不会影响其他的二进制位；DNA 序列异或和二进 制异或结果则相同。 加密步骤： （1）首先读取一幅大小为 M × N 大小的灰度图像 A 。 （2）对图像 A 进行位平面的分解，得到 8 幅位平面 图像，由于低位包含的图像信息少，为了减少置乱的时 间，将图像的低 4 位图像合并成 1 幅图像，得到 5 幅图像。 （3）输入混沌映射Logistic和Kent的初始值 x_logistic 、 x_kent 和控制参数 μ_logistic 、p_kent ，使用 Hash 函数 获得图像的 Hash 值，用图像的 Hash 值对混沌映射的初 始值和控制参数进行处理，获得图像的加密密钥，设置 位置截取参数 δ1、δ2、δ3 ，舍弃前面部分序列值后，生成 3 个混沌序列值。由 Logistic 映射生成的两个混沌映射 分别用来对位平面的图像进行置乱和生成对置乱后图 像进行 DNA 编码规则、DNA 运算规则的索引。由 Kent 映射生成的混沌序列用于生成与加密图像等大小的图 像，进行 DNA 运算。 （4）将由 Logistic 生成的去掉前 δ1 项的混沌序列转 换成与二进制图像等大小的矩阵 (M*N × 5) ，并按照矩 阵的列进行排序，将排序后的 Logistic 映射序列在原 Logistic 映射序列的位置保存在矩阵 T 中，使用矩阵 T 对图像在位平面进行置乱，得置乱后的图像。 图像的解密与加密过程类似，是加密的逆过程，在 解密的过程中用到与 DNA 加法运算相反的 DNA 减法 运算进行解密。 4 实验结果与分析 利用本文提出的基于混沌映射的位变换和 DNA 序列的图像加密算法对图像进行加密和解密实验。加 密 密 钥为 x_logistic = 0.27、x_kent = 0.205、μ_logistic = 3.897 6、p_kent = 0.215、δ1 = δ2 = δ3 = 200 时，图像的加 密图像见图 2。 （a）Lena 原图 （b）Lena 加密图 图 2 明文图像和密文图像 4.1 密钥空间分析 密钥空间是指加密算法中的所有密钥的取值空间， 好的加密算法的密钥空间应当能够防止使用穷举的方 式暴力破解，保证整个加密系统的安全性。 本文的密钥空间主要是混沌映射的初值和控制参 数，主要包括 x_logistic、x_kent、μ_logistic、p_kent ，密 钥都是双精度实数，具有 15 位可变十进制小数，密钥 空间为 1015×1015×1015×1015 2199，因此该加密算法具有巨 大的密钥空间，可以有效抵御密钥的穷举攻击，安全性 较强。 4.2 密钥敏感性分析 ≈ 密钥的敏感性分析是使一个密钥在其他密钥不变 的情况下，发生微小的变化，然后用其解密已加密的图 像。图 3 是 4 个密钥在其他 3 个密钥不变的情况下，改 变 10－15后对加密图像的解密图像。 实验结果表明，密钥的微小改变，会严重影响解密 图像的效果，无法找到原图像的任何信息，图像变得杂 计算机工程与应用www.ceaj.org

94 2018，54（5） Computer Engineering and Applications 计算机工程与应用 （a）改变 x_logistic （b）改变 μ_logistic （c）改变 x_kent （d）改变 p_kent 图 3 图像密钥的敏感性 乱无章。因此该算法具有较好的保密安全性。 4.3 直方图分析 直方图是图像像素值的有序分布图，可以依据密文 图像的灰度直方图评价图像加密算法的性能。图 4 是 原图像和加密图像的灰度直方图。 数 个 素 像 700 600 500 400 300 200 100 0 数 个 素 像 0 50 100 150 200 250 灰度值 600 500 400 300 200 100 0 0 50 100 150 200 250 灰度值 图 4 明文图像和密文图像的直方图 从图 4 可以看到，密文图像的直方图，分布均匀，原 图像的统计特性被打破，因此，该加密算法又有较好的 抗统计分析的性能。 4.4 相关性分析 相关性是指图像相邻像素灰度值的相关程度，相关 系数越小，像素的相关性越低，抗统计分析能力越强。 表 5 和图 5 分别是明文图像和加密图像像素的相关系数 和相关图像。 表 5 明文图像和密文图像的相关系数 明文 密文 文献[14] 文献[20] 水平方向 竖直方向 对角方向 0.968 9 0.006 3 0.002 0 －0.057 4 0.940 2 0.002 1 －0.000 7 －0.003 5 0.921 4 0.009 8 －0.001 4 0.057 8 表 5 以 Lena 图像为例，分别从水平、竖直、对角方向 随机选择相邻的像素进行分析，得到对应的相关系数， 并与文献[14]、[20]对比，加密图像的相关性已经优于文 献[20]。 通过表 5 和图 5 可以得出，加密图像相邻像素的相 关性变得非常低。现阶段，混沌加密图像相邻像素的相 值 度 灰 的 ） ，y 1 + x （ 点 值 度 灰 的 ） 1 + ，y （ 点 x 值 度 灰 的 ） 1 + ，y 1 + x （ 点 250 200 150 100 50 0 100 150 200 250 50 点（x，y）的灰度值 （a1）明文水平方向 250 200 150 100 50 0 100 150 200 250 50 点（x，y）的灰度值 （a2）明文竖直方向 250 200 150 100 50 0 100 150 200 250 50 点（x，y）的灰度值 （a3）明文对角方向 值 度 灰 的 ） ，y 1 + x （ 点 值 度 灰 的 ） 1 + ，y （ 点 x 值 度 灰 的 ） 1 + ，y 1 + x （ 点 300 250 200 150 100 50 0 100 150 200 250 300 50 点（x，y）的灰度值 （b1）密文水平方向 300 250 200 150 100 50 0 100 150 200 250 300 50 点（x，y）的灰度值 （b2）密文竖直方向 300 250 200 150 100 50 0 100 150 200 250 300 50 点（x，y）的灰度值 （b3）密文对角方向 图 5 明文图像和密文图像的相关性 关性只要能达到小数点后两位就认为效果已经理想。 因此，本文的加密算法达到了理想的加密效果。 4.5 信息熵分析 图像的信息熵是用来度量图像的混乱程度，度量灰 度值的分布，图像的信息熵越大，其灰度分布越一致， 对理想的随机图像，其信息熵等于 8。一个有效的加密 算法应该使加密图像的信息熵接近于 8。表 6 列出了 Lena、Baboon、Cameraman、Peppers 4 幅图像加密之后 的信息熵，同时给出了文献[14]、[21-22]的实验结果。 由表 6 中的信息熵可知，本文的加密算法在信息熵方面 优于所列文献。 表 6 密文图像的信息熵 算法 本文 文献[14] 文献[21] 文献[22] Lena 7.997 4 7.997 0 7.987 4 7.997 0 Baboon 7.997 3 7.996 9 — Cameraman 7.997 0 7.997 2 — 7.997 4 7.996 7 Peppers 7.996 8 — 7.986 0 — 4.6 经典攻击 经典攻击类型主要包括以下四种： (1）唯密文攻击：密码分析者仅知道一些密文。 （2）已知明文攻击：密码分析者知道一些明文和相 应密文。 （3）选择明文攻击：密码分析者可以选择一些明文， 并得到相应的密文。 （4）选择密文攻击：密码分析者可以选择一些密文， 计算机工程与应用www.ceaj.org0100200300400500600700(a) Lena??????0501001502002500100200300400500600(b) Lena??????0501001502002500100200300400500600700(a) Lena??????0501001502002500100200300400500600(b) Lena??????050100150200250

施 飞，张红梅，张向利：基于混沌映射和 DNA 编码的图像加密算法 2018，54（5） 95 并得到相应的明文。 现代密码学原理中提到加密体系的安全性并不依 赖于加密方法本身，而是依赖于所使用的密钥，因此，本 文提出的加密算法为了提高算法的安全性，将明文信息 通过 Hash 函数与密钥进行结合，生成最终的密钥，能够 更好地抵御选择明文攻击。 5 结束语 本文提出一种基于混沌映射的位变换和 DNA 序列 的图像加密算法，该算法在位平面对像素灰度值进行置 乱，能够达到像素置乱和扩散的效果；然后使用 DNA 对 置乱后的图像进行编码，使用 DNA 运算对图像的像素 进行扩散。理论分析和实验结果表明，该算法密钥空间 足够大，灰度直方图成均匀分布，密钥足够敏感，像素之 间的相关性较低，信息熵接近于 8。因此，该加密算法具 有较好的实用性和安全性。 参考文献： [1] Rublee E，Rabaud V，Konolige K，et al.ORB：An efficient alternative to SIFT or SURF[C]//International Conference on Computer Vision，2011：2564-2571. [2] Patidar V，Pareek N K，Purohit G，et al.A robust and secure chaotic standard map based pseudo random per- mutation-substitution scheme for image encryption[J]. Optics Communications，2011，284（19）：4331-4339. [3] 张小华，刘芳，焦李成 . 一种基于混沌序列的图像加密技 术[J]. 中国图象图形学报，2003，8（4）：374-378. [4] 李晓轩，王阿川 . 一种基于混沌排序的数字图像置乱算 法[J]. 黑龙江科技信息，2009（27）. [5] 顾勤龙，姚明海 . 基于 Logistic 混沌序列的数字图像加密 研究[J]. 计算机工程与应用，2003，39（23）：114-116. [6] Mathews R，Goel A，Saxena P，et al.Image encryption based on explosive inter-pixel displacement of the RGB attributes of a pixel[C]//Proceedings of the World Congress on Engineering and Computer Science，2011：19-21. [7] Pareek N K，Patidar V，Sud K K.Image encryption using chaotic logistic map[J].Image and Vision Computing，2006， 24（9）：926-934. [8] 曹建秋，萧华荣，蓝章礼 . 像素位置与像素值双重置换的混 沌加密算法[J]. 计算机工程与应用，2010，46（28）：192-195. [9] Liu H，Wang X.Color image encryption based on one- time keys and robust chaotic maps[J].Computers & Mathematics with Applications，2010，59（10）：3320-3327. [10] Adleman L M.Molecular computation of solutions to combinational problems[J].Science，1994，266（11）：1021- 1024. [11] Xiao G，Lu M，Qin L，et al.New field of cryptography： DNA cryptography[J].Chinese Science Bulletin，2006，51 （12）：1413-1420. [12] 房东鑫，张健 . 基于猫映射和 DNA 编码的图像加密算 法[J]. 计算机工程，2014，40（12）：89-93. [13] 张健，房东鑫 . 应用混沌映射索引和 DNA 编码的图像加 密技术[J]. 计算机工程与设计，2015，36（3）：613-618. [14] Wang X Y，Zhang Y Q，Bao X M.A novel chaotic image encryption scheme using DNA sequence operations[J]. Optics and Lasers in Engineering，2015，73：53-61. [15] Wong K W，Kwok B，Law W S，et al.A fast image encryption scheme based on chaotic standard map[J]. Physics Letters A，2008，372（15）：2645-2652. [16] Ye R.A highly secure image encryption scheme using compound chaotic maps[J].Journal of Emerging Trends in Computing and Information Sciences，2013，4（6）. [17] Xu Z，Tian Q，Tian L.An image encryption method based on independently and uniformly distributed chaotic key stream[J].Journal of Information and Computational Science，2013，10（18）：5971-5980. [18] Zhou S，Wang B，Zheng X，et al.An image encryption scheme based on DNA computing and cellular automata[J]. Discrete Dynamics in Nature and Society，2016. [19] Ye R，Xi Y，Ye M，et al.A multiple tent maps based image encryption scheme with plain- image dependent permutation and diffusion[EB/OL].（2015）.https：//www. researchgate.net/publication/301369795_A_Multiple_Tent_ Maps_Based_Image_Encryption_Scheme_with_Plain-image_ Dependent_Permutation_and_Diffusion. [20] Liu H，Wang X.Color image encryption using spatial bit- level permutation and high-dimension chaotic system[J]. Optics Communications，2011，284（16）：3895-3903. [21] Liu H，Wang X.Image encryption using DNA comple- mentary rule and chaotic maps[J].Applied Soft Computing， 2012，12（5）：1457-1466. [22] Wang X，Liu L，Zhang Y.A novel chaotic block image encryption algorithm based on dynamic random growth technique[J].Optics and Lasers in Engineering，2015，66： 10-18. 计算机工程与应用www.ceaj.org