第1页 / 共9页
第2页 / 共9页
第3页 / 共9页
第4页 / 共9页
第5页 / 共9页
第6页 / 共9页
第7页 / 共9页
第8页 / 共9页
论文研究 - 基于FFT循环相关的GPS信号快速采集方法。.pdf
Fast Acquisition Method of GPS Signal Based on FFT Cyclic Correlation
Abstract
Keywords
1. Introduction
2. GPS Signal Acquisition Based on Time Domain Correlation
2.1. Implementation Ideas and Processes
2.2. Simulation Results and Analysis
3. GPS Signal Acquisition Based on FFT Cyclic Correlation
3.1. Implementation Ideas and Processes
3.2. Simulation Results and Analysis
4. Analysis and Comparison of GPS Signal Acquisition Methods
4.1. Calculating Time
4.2. Time Delay Error
5. Conclusion
Acknowledgements
References
Int. J. Communications, Network and System Sciences, 2017, 10, 246-254
http://www.scirp.org/journal/ijcns
ISSN Online: 1913-3723
ISSN Print: 1913-3715
Fast Acquisition Method of GPS Signal Based on
FFT Cyclic Correlation
Hao Cui, Zhigang Li, Zheng Dou
College of Information and Communication Engineering, Harbin Engineering University, Harbin, China
How to cite this paper: Cui, H., Li, Z.G.
and Dou, Z. (2017) Fast Acquisition Me-
thod of GPS Signal Based on FFT Cyclic Cor-
relation. Int. J. Communications, Network
and System Sciences, 10, 246-254.
https://doi.org/10.4236/ijcns.2017.108B026
Received: June 24, 2017
Accepted: August 11, 2017
Published: August 14, 2017
Abstract
Since the global positioning system began to operate, it has become more and
more close to people’s lives, and has been applied to various fields now. In
order to track and decode GPS signals, GPS signals need to be captured first.
The necessary parameters of the captured GPS signal are immediately trans-
mitted to the tracking process, and then the navigation message of the satellite
can be obtained by tracking process. In this paper, the basic contents related
to the signal structure of GPS system are briefly described. Then, the tradi-
tional GPS signal acquisition method based on time domain correlation me-
thod is introduced, and the GPS signal acquisition method based on FFT cyc-
lic correlation method is discussed in this paper. By comparing the simulation
results, two kinds of GPS signal acquisition methods are compared with the
calculation time according to the method of controlling variables. For the two
GPS signal acquisition methods, the variation of time delay error with SNR is
simulated in this paper.
Keywords
GPS, FFT, Satellite Signal, Acquisition, Circular Correlation
1. Introduction
Using GPS system for positioning and navigation, we need to capture the GPS
signal at first. In the GPS receiver, the local generated carrier and spread spec-
trum code need to synchronize with the carrier and spread spectrum code in the
received signal. This synchronization is generally divided into two stages: coarse
synchronization and fine synchronization [1]. The acquisition process is to es-
timate the Doppler shift and the pseudo code phase of the received signal and
initialize the tracking loop with these estimates. There are two kinds of com-
monly used GPS signal acquisition methods, sliding correlation method and
matched filter capture method [2]. The sliding correlation method takes serial
DOI: 10.4236/ijcns.2017.108B026 August 14, 2017
H. Cui et al.
search in time domain and frequency domain, and makes correlation between
1023 code phases of each frequency. This method is simple, but the search time
is too long. Although the matching filter can achieve a certain degree of parallel
computing, not affected by the pseudo code cycle, but it will take up a lot of
hardware resources [3]. In order to get a balance between search speed and re-
sources, this paper uses FFT-based acquisition method, serial search in the time
domain and frequency domain are in parallel, so as to improve the acquisition
speed and not occupy too much resources.
2. GPS Signal Acquisition Based on Time Domain Correlation
2.1. Implementation Ideas and Processes
The signal of the GPS contains three parts: carrier signals (L1 and L2), spread
spectrum sequences (C/A codes, P codes or Y codes) and navigation data (D
codes) [4]. The local code is represented as a form of C/A code multiplied by an
RF signal. The radio frequency signal RF is a complex number, and the local
code is multiplied by the RF code and the C/A code [5]. Assuming that the L1
frequency (1575.42 MHz) is down converted to 21.25 MHz, digitized at a rate of
5 MHz to obtain an output frequency of 1.25 MHz. The frequency range of the
capture program is (1250 ± 10) kHz, step 1 kHz, and a total of 21 frequency
components. The local code can be expressed as:
j
2
C e π
s
f t
i
si
l
=
In the above equation, the subscript s represents the satellite number,
(1)
sC is
if = 1250 − 10, 1250 − 9, ···, 1250 + 10 kHz. The
the C/A code of the satellite S,
local signal must also be digitized at a 5 MHz sampling rate to produce 5000 data
points.
The above 21 sets of data (only corresponding to a satellite C/A code) re-
presents 21 frequencies at intervals of 1 kHz. If the C/A code and the frequency
of the local signal are correct, and the C/A code phase is aligned, the output is
maximized. The flow chart of the acquisition process is as shown in Figure 1:
Input Data
1
2
k
Locally Generated Data f1
Output 1
Locally Generated Data f2
Output 2
Locally Generated Data fk
Output k
21
Locally Generated Data f21
Figure 1. Acquisition method based on time domain correlation method.
Output 21
247
H. Cui et al.
The operation of the group is as follows: the digitized input signal and the lo-
cally generated signal are multiplied by a point (5000 points in total). The square
of the product is added to the square of the imaginary part and the square root is
the magnitude of the output frequency. Every 200 ns carries on the above opera-
tion to the data, after the input data shift 5000 points, has completed the search
to the 1ms data, altogether outputs 5000 magnitude values. 21 groups of local
signals output 105,000 (5000 × 21) amplitude values. In these amplitude values,
the maximum frequency component beyond the threshold corresponds to the
Doppler frequency. The maximum value corresponding to the data shift K is the
starting position of the C/A code [6].
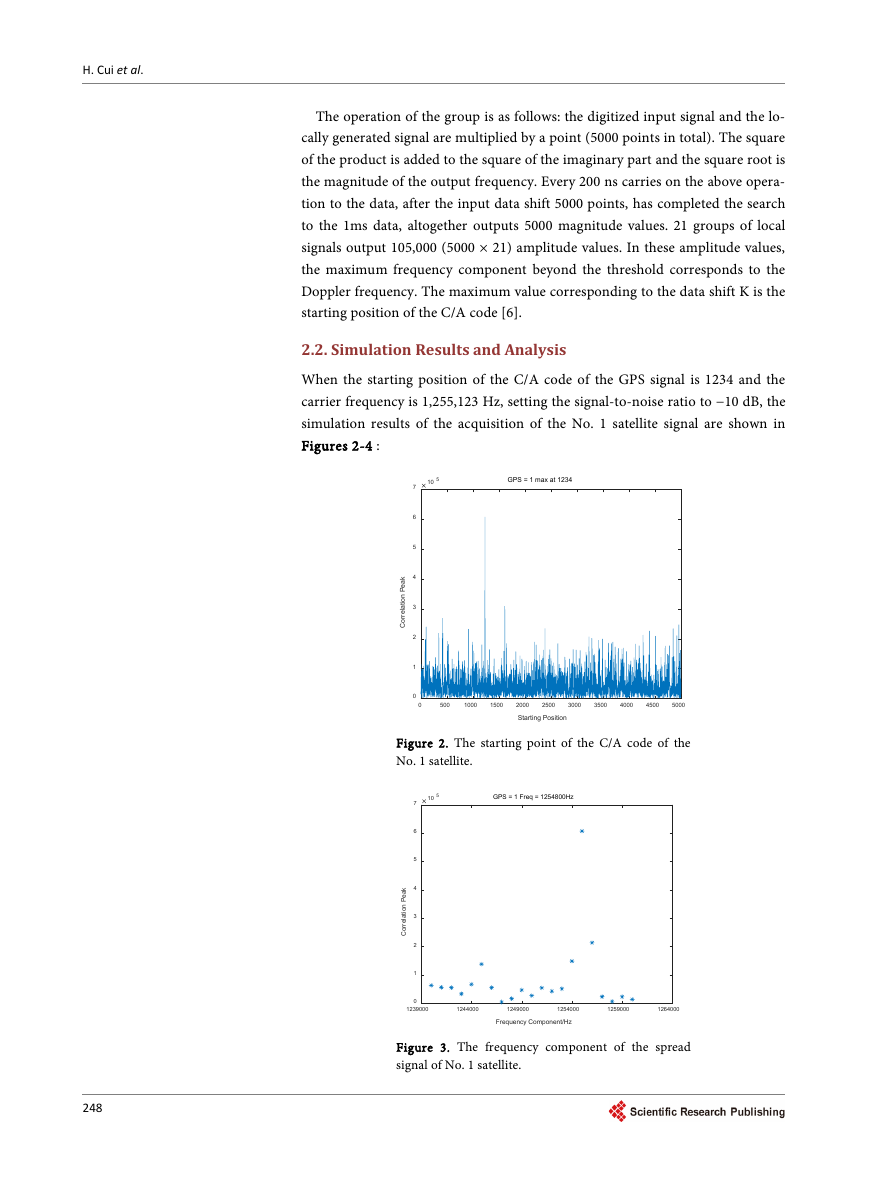
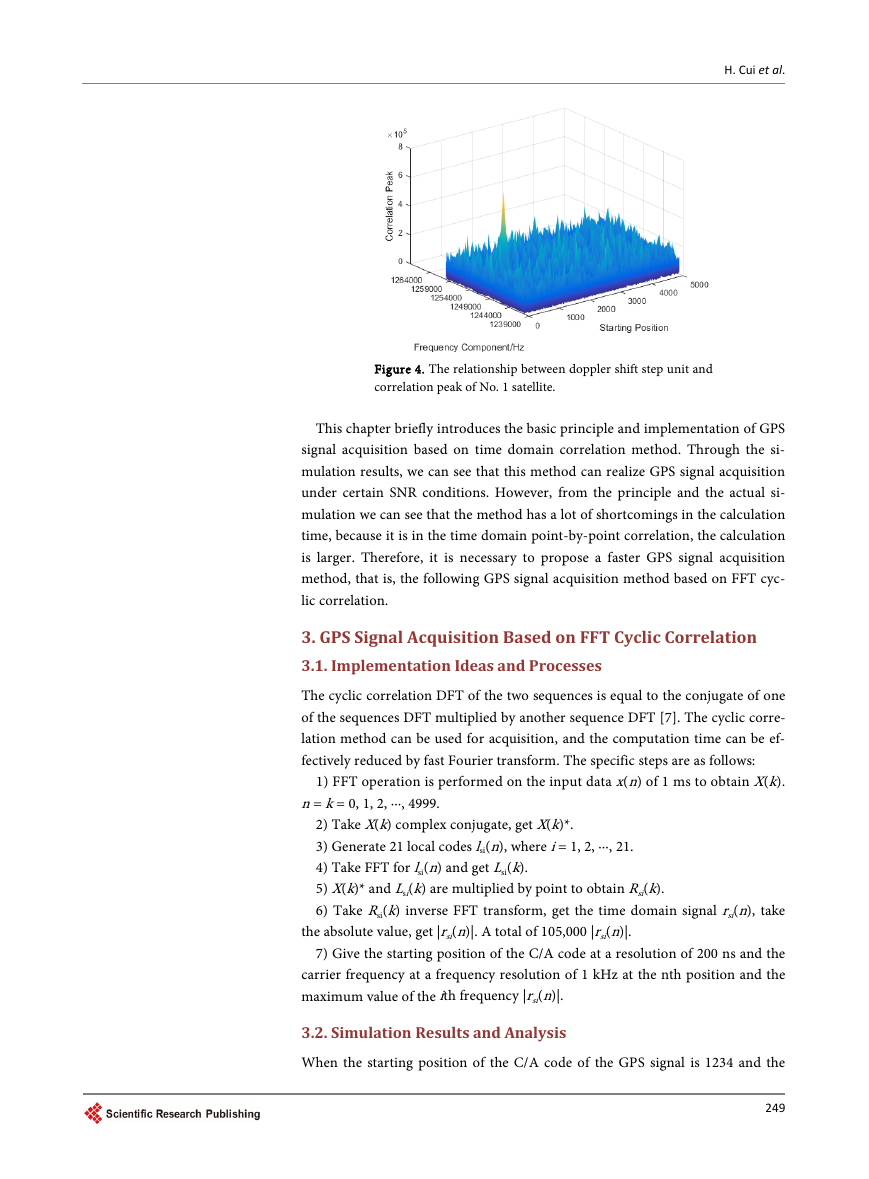
2.2. Simulation Results and Analysis
When the starting position of the C/A code of the GPS signal is 1234 and the
carrier frequency is 1,255,123 Hz, setting the signal-to-noise ratio to −10 dB, the
simulation results of the acquisition of the No. 1 satellite signal are shown in
Figures 2-4 :
10 5
GPS = 1 max at 1234
7
6
5
4
3
2
1
0
k
a
e
P
n
o
i
t
l
a
e
r
r
o
C
0
500
1000
1500
3000
3500
4000
4500
5000
2500
2000
Starting Position
Figure 2. The starting point of the C/A code of the
No. 1 satellite.
10 5
GPS = 1 Freq = 1254800Hz
7
6
5
4
3
2
1
0
k
a
e
P
n
o
i
t
l
a
e
r
r
o
C
1239000
1244000
1249000
1254000
1259000
1264000
Frequency Component/Hz
Figure 3. The frequency component of the spread
signal of No. 1 satellite.
248
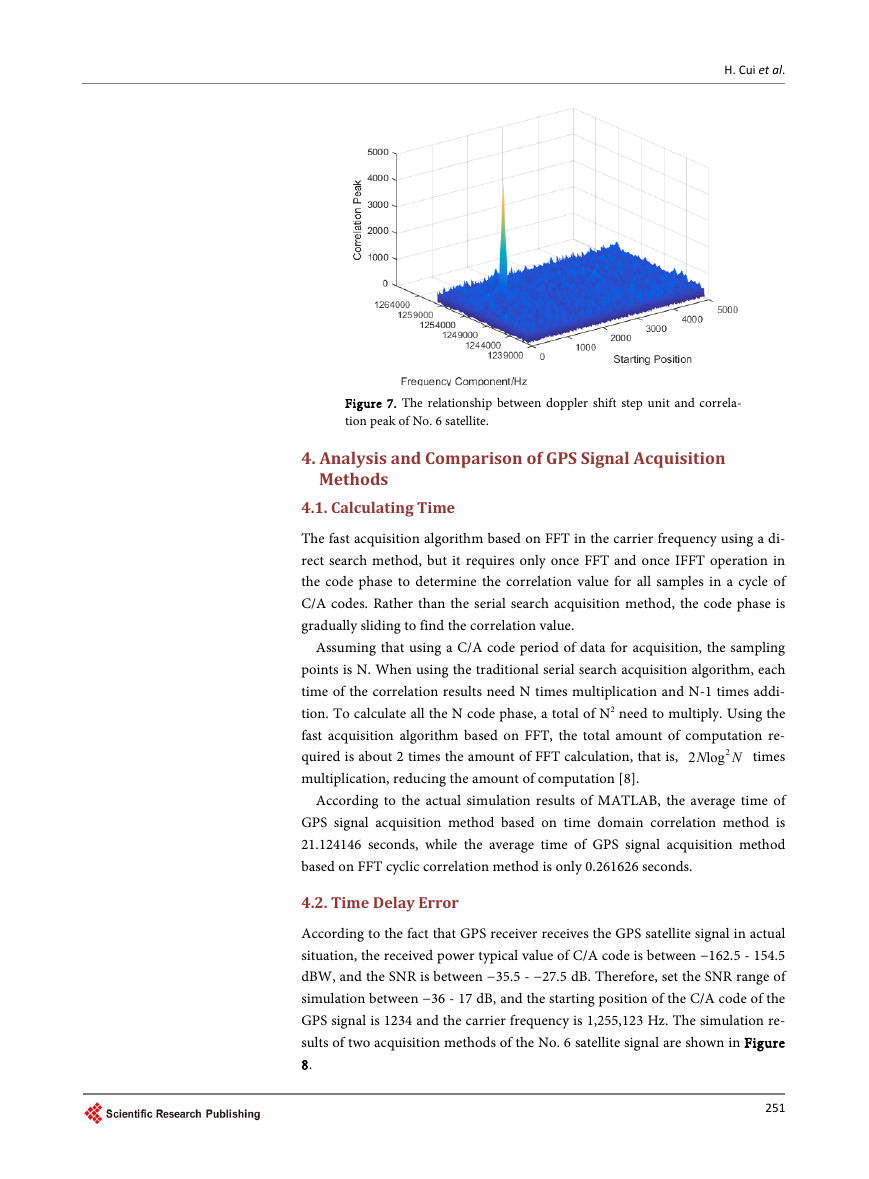
H. Cui et al.
Figure 4. The relationship between doppler shift step unit and
correlation peak of No. 1 satellite.
This chapter briefly introduces the basic principle and implementation of GPS
signal acquisition based on time domain correlation method. Through the si-
mulation results, we can see that this method can realize GPS signal acquisition
under certain SNR conditions. However, from the principle and the actual si-
mulation we can see that the method has a lot of shortcomings in the calculation
time, because it is in the time domain point-by-point correlation, the calculation
is larger. Therefore, it is necessary to propose a faster GPS signal acquisition
method, that is, the following GPS signal acquisition method based on FFT cyc-
lic correlation.
3. GPS Signal Acquisition Based on FFT Cyclic Correlation
3.1. Implementation Ideas and Processes
The cyclic correlation DFT of the two sequences is equal to the conjugate of one
of the sequences DFT multiplied by another sequence DFT [7]. The cyclic corre-
lation method can be used for acquisition, and the computation time can be ef-
fectively reduced by fast Fourier transform. The specific steps are as follows:
1) FFT operation is performed on the input data x(n) of 1 ms to obtain X(k).
n = k = 0, 1, 2, ···, 4999.
2) Take X(k) complex conjugate, get X(k)*.
3) Generate 21 local codes lsi(n), where i = 1, 2, ···, 21.
4) Take FFT for lsi(n) and get Lsi(k).
5) X(k)* and Lsi(k) are multiplied by point to obtain Rsi(k).
6) Take Rsi(k) inverse FFT transform, get the time domain signal rsi(n), take
the absolute value, get |rsi(n)|. A total of 105,000 |rsi(n)|.
7) Give the starting position of the C/A code at a resolution of 200 ns and the
carrier frequency at a frequency resolution of 1 kHz at the nth position and the
maximum value of the ith frequency |rsi(n)|.
3.2. Simulation Results and Analysis
When the starting position of the C/A code of the GPS signal is 1234 and the
249
H. Cui et al.
carrier frequency is 1,255,123 Hz, setting the signal-to-noise ratio to −10 dB, the
simulation results of the acquisition of the No. 6 satellite signal are shown in
Figures 5-7.
This chapter gives the GPS acquisition method based on FFT cyclic correla-
tion, introduces its basic principle and implementation process, and then gives
the simulation results. In the code phase, the fast acquisition algorithm based on
FFT requires only one FFT and one IFFT operation to determine the correlation
value for all samples in a cycle of C/A codes. Rather than the serial search acqui-
sition method, the code phase is gradually sliding to find the correlation value.
And it greatly reduces the amount of calculation.
GPS = 6 max at 1234
5000
4500
4000
3500
3000
2500
2000
1500
1000
500
k
a
e
P
n
o
i
t
l
a
e
r
r
o
C
0
0
500
1000
1500
2500
2000
Starting Position
3000
3500
4000
4500
5000
Figure 5. The starting point of the C/A code of the No. 6 satellite.
GPS = 6 Freq = 1254800Hz
5000
4500
4000
3500
3000
2500
2000
1500
1000
500
k
a
e
P
n
o
i
t
l
a
e
r
r
o
C
0
1239000
1244000
1249000
1254000
1259000
1264000
Frequency Component/Hz
Figure 6. The frequency component of the spread signal of No. 6 satel-
lite.
250
H. Cui et al.
Figure 7. The relationship between doppler shift step unit and correla-
tion peak of No. 6 satellite.
4. Analysis and Comparison of GPS Signal Acquisition
Methods
4.1. Calculating Time
The fast acquisition algorithm based on FFT in the carrier frequency using a di-
rect search method, but it requires only once FFT and once IFFT operation in
the code phase to determine the correlation value for all samples in a cycle of
C/A codes. Rather than the serial search acquisition method, the code phase is
gradually sliding to find the correlation value.
Assuming that using a C/A code period of data for acquisition, the sampling
points is N. When using the traditional serial search acquisition algorithm, each
time of the correlation results need N times multiplication and N-1 times addi-
tion. To calculate all the N code phase, a total of N2 need to multiply. Using the
fast acquisition algorithm based on FFT, the total amount of computation re-
quired is about 2 times the amount of FFT calculation, that is,
N times
multiplication, reducing the amount of computation [8].
2 logN
2
According to the actual simulation results of MATLAB, the average time of
GPS signal acquisition method based on time domain correlation method is
21.124146 seconds, while the average time of GPS signal acquisition method
based on FFT cyclic correlation method is only 0.261626 seconds.
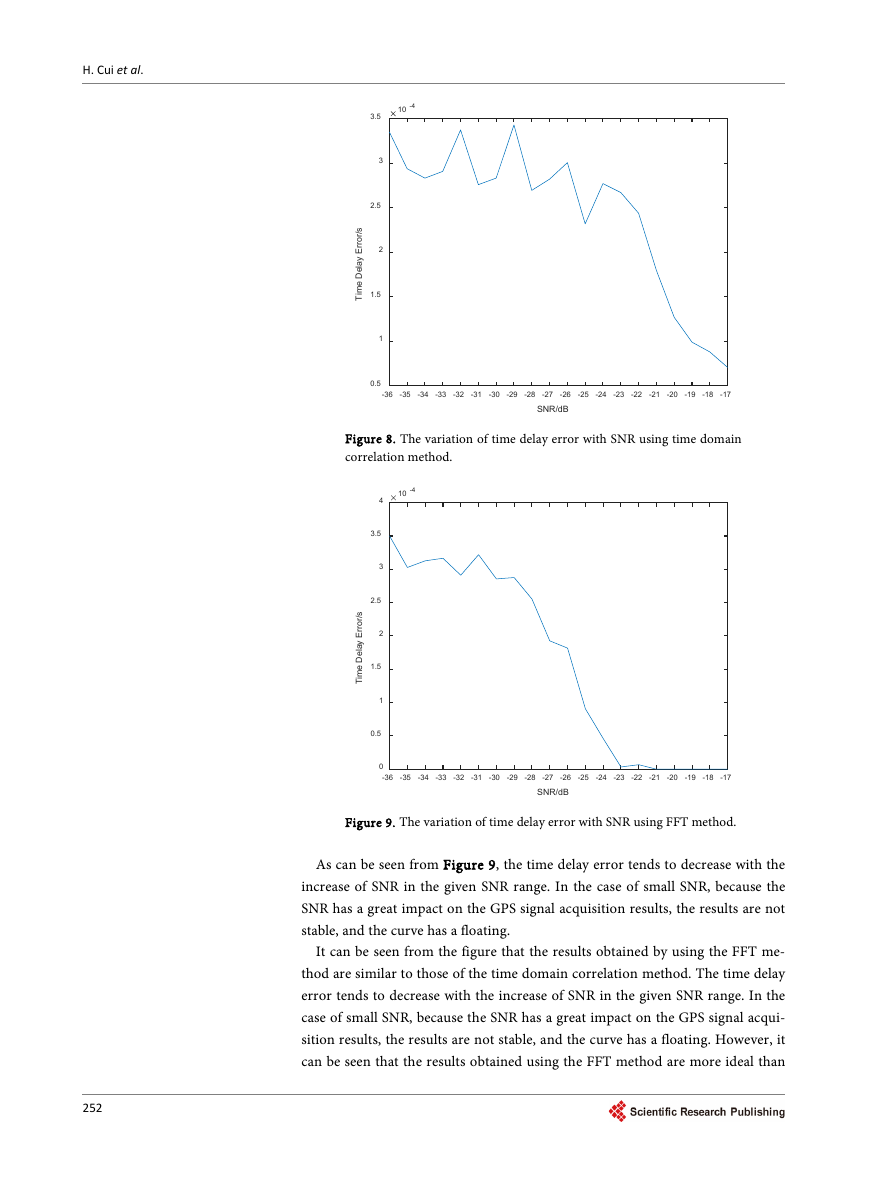
4.2. Time Delay Error
According to the fact that GPS receiver receives the GPS satellite signal in actual
situation, the received power typical value of C/A code is between −162.5 - 154.5
dBW, and the SNR is between −35.5 - −27.5 dB. Therefore, set the SNR range of
simulation between −36 - 17 dB, and the starting position of the C/A code of the
GPS signal is 1234 and the carrier frequency is 1,255,123 Hz. The simulation re-
sults of two acquisition methods of the No. 6 satellite signal are shown in Figure
8.
251
H. Cui et al.
10 -4
3.5
3
2.5
2
1.5
1
0.5
s
/
r
o
r
r
l
E
y
a
e
D
e
m
T
i
-36 -35 -34 -33 -32 -31 -30 -29 -28 -27 -26 -25 -24 -23 -22 -21 -20 -19 -18 -17
Figure 8. The variation of time delay error with SNR using time domain
correlation method.
SNR/dB
10 -4
4
3.5
3
2.5
2
1.5
1
0.5
s
/
r
o
r
r
l
E
y
a
e
D
e
m
T
i
0
-36 -35 -34 -33 -32 -31 -30 -29 -28 -27 -26 -25 -24 -23 -22 -21 -20 -19 -18 -17
Figure 9. The variation of time delay error with SNR using FFT method.
SNR/dB
As can be seen from Figure 9, the time delay error tends to decrease with the
increase of SNR in the given SNR range. In the case of small SNR, because the
SNR has a great impact on the GPS signal acquisition results, the results are not
stable, and the curve has a floating.
It can be seen from the figure that the results obtained by using the FFT me-
thod are similar to those of the time domain correlation method. The time delay
error tends to decrease with the increase of SNR in the given SNR range. In the
case of small SNR, because the SNR has a great impact on the GPS signal acqui-
sition results, the results are not stable, and the curve has a floating. However, it
can be seen that the results obtained using the FFT method are more ideal than
252
H. Cui et al.
the time domain correlation method, and the floating is relatively small.
5. Conclusion
The demand of positioning and navigation has been developing with human ci-
vilization, and playing an important role in the development of human history.
Not only in defense and military, but also in the civil field it has shown a huge
application prospects and broad commercial market, changing everyone’s habits
and ways of thinking. In order to track and decode GPS signals, GPS signals
need to be captured first. In this paper, the traditional GPS signal acquisition
method based on time domain correlation method is introduced, and the GPS
signal acquisition method based on FFT cyclic correlation method is discussed.
Through the actual simulation and analysis, it is not difficult to conclude that
the GPS signal acquisition method based on FFT has more advantages than the
traditional time domain correlation method in terms of calculating time and
acquisition performance. Therefore, the proposed GPS signal acquisition me-
thod based on FFT is a feasible and superior GPS signal acquisition method.
Acknowledgements
This paper is funded by the International Exchange Program of Harbin Engi-
neering University for Innovation-oriented Talents Cultivation, National Natu-
ral Science Foundation of China (No. 61401115), National Natural Science
Foundation of China (No. 61301095), National Natural Science Foundation of
China (No. 61671167), International Science & Technology Cooperation Pro-
gram of China (2014 DFR10240), China Postdoctoral Science Foundation (2013-
T60346), Harbin Science and Technology Research Projects (P083313026), Nat-
ural Science Foundation of Heilongjiang Province (P083014025).
References
[1] Chang, L., Zhang, J., Zhu, Y. and Pan, Q. (2011) Analysis and Optimization of PMF-
FFT Acquisition Algorithm for High-Dynamic GPS Signal. IEEE International Con-
ference on Cybernetics and Intelligent Systems, Qingdao, 17-19 September 2011, 85-
189. https://doi.org/10.1109/iccis.2011.6070325
[2] Napolitano, A. and Perna, I. (2014) Cyclic Spectral Analysis of the GPS Signal. Digi-
tal Signal Processing, 33, 13-33. https://doi.org/10.1016/j.dsp.2014.06.003
[3] Van Nee, D.J.R. and Coenen, A.J.R.M. (1991) New Fast GPS Code-Acquisition
Technique Using FFT. Electronics Letters, 27, 158-160.
https://doi.org/10.1049/el:19910102
[4] Ahamed, S.F., Laveti, G., Goswami, R. and Rao, G.S. (2016) Fast Acquisition of GPS
Signal Using Radix-2 and Radix-4 FFT Algorithms. IEEE International Conference
on Advanced Computing, Bhimavaram, 27-28 February 2016, 674-678.
https://doi.org/10.1109/iacc.2016.130
[5] Patel, V. and Shukla, P. (2011) Faster Methods for GPS Signal Acquisition in Fre-
quency Domain. International Conference on Emerging Trends in Networks and
Computer Communications, 84-88.
[6] Jan, S.S. and Lin, Y.C. (2009) A New Multi-c/a Code Acquisition Method for GPS.
GPS Solutions, 13, 293-303. https://doi.org/10.1007/s10291-009-0122-7
253
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
