第 22卷 第 4期 2011年 12月 广 西 工 学 院 学 报 JOURNAL OF GUANGⅪ UNIVERSrI 0F IECHNOIDGY V0】．22 No．4 Dec．2011 文章编号 1004．6410(201 1)04．0035．05 基于动态规划算法 的机器人避 障路径研究 张 昊 ，罗文广 ，臧 庆 凯 (广西工学院 电子信息与控制工程系 ，广西 柳州 545006) 摘 要 ：为 了使 复 杂 的 移 动 机 器 人 路 径 规 划 问题 得 到 简 化 ，并 减 少 可行 路径 的 计 算 量 ．对 避 障 路 径 规 划 问题 进行 了 比 较 深 入 的 研究 ．在 以可 视 图 法 所 建 的 求 解 环 境 为 基 础 上 ，将 避 障路 径 规 划 转 化 为 多 阶段 决 策 问 题 。对 每 一个 阶段 的子 问题应用 改进可视 图法 和几何逼 近算 法进 行求解 ，得出各阶段 的最 短路径．验证表明 ：该 算法是一种正确 、高效 。实用 的算 法 ． 关键 词 ：蔽 障路 径 规 划 ；动 态 规 划 ；可 视 图 ；最优 路 径 中 图分 类 号 ：TP249 文 章标 志码 ：A 0 引言 移动机器人路径规划是指在有 障碍物 的工作环境 中。如何寻找一条从 给定起点到给定 目标点的运动 路径 ，使机器人在运动过程 中能安全无碰撞地绕过所有障碍物【l ，并尽量满足如时间最短 ，耗能最低等某 些优化指标．根据机器人对环境信息知道的程度不同 ，路径规划可 以分为两种类型 ：1)环境信息完全 已知的 全局路径规划 ，又称静态或离线路径规划 ；2)环境信息完全未知或部分 未知 ，通过传感器在线地对机器人 工作环境进行探测 ，以获取 障碍物的位置 、形状和尺寸等信息 的局部路径规划 ，又称动态或在线路径规划． 全局路径规划常用的方法有 ：可视 图法 [3]、栅 格法 、自由空 间法等．基 于图论 的全局路径规划 的基本思 想是构造某种图来描述环境的 自由空间 ，从图上找到满足某种准则的最优路径．此法一般包括两个 阶段 ：第 一 阶段构造一个用 以描述 自由空 间的关系图；第二 阶段按照一定 的准则(如最短距离 ，最少时间等 )寻求一 条最优路径．本文就视图法 中利用动态规划算法对移动机器人路径规划进行设计． 1 可 视 图法 可视 图法视移动机器人 为一 点 ，将机器人起始点、目标点和多边 形障碍物的各顶点进行组合连接 ，并 保证这些直线均不与障碍物相交 ，构成一 张无 向图 ，称为可视 图．由于任 意两直线 的顶点都是可见 的 ，从起 点沿着这些直线到达 目标点 的所有路径均是运动物体的无碰路径．搜索最优路 径的问题就转化为从起点 到 目标点 ，经过这些可视直线的最短距离问题．在实际应用 中，机器人不可能只是空间中的一个点 ，这就需 要 对 上述 可视 图构 建方 法 进 行 修正 ．从 路径 规 划 的角 度 来说 ，机 器 人 缩 小一 定 尺 寸 ，同障 碍物 外 扩相 应 尺寸 是等价的，因此可 以根据机器人 的物理尺寸和运动方式 ，对空间障碍 物进行 增长操 作 ，在障碍物增 长后 的 环境中。机器人可 以视为一点 ，从而可 以继续采用上述方法构建可视 图． 目前 ，利用可视图对最短路径 的求解方法有 ：贪心算法 、Dijkstra算法 、A：I：算法．相 比来说 。贪心算法采 用逐步构造最优解 ，每个 阶段都做 出一个 看上去最优 的决策 ，一旦做 出就不再更改 ，所 以并不一定得 出整 体最 优解 ；Dijkstra算法效率低 ，运算 中占用空 间大 ，需要 3n(n一1)／2次运 算 (11,为节点数 )；A：I：算法 ：在同 收穑 日期 ：2011-06-17 基金项目：广西 自然科学基金项 目 (桂科 自 0832067)资助． 通信作者 ：罗文广 。教授 ，工学硕士 ，研究方 向：智能控制及应用 ，E-mail：1wg168@126．corn． 

36 广 西 工学 院学 报 第 22卷 样 的前 提 下 ，选 用 不 同 的估 价 函数 ，所 需 搜 索 的节 点 数 目和 最终 的搜 索 结 果 可 能 不 同．实 际 情 况 中需要 依 据经验来合理构造估价函数 ．本文根据 以上算法存在的缺点 。利用动态规范算法将避 障路径规划转化为一 个 多 阶段决 策 问题 ，从 而 将 问题 与动 态 规划 有 效 地结 合 在一 起 ，对 于 每 一 个 阶 段 的子 问题 应 用 改 进可 视 图 法 和几 何 逼 近 算 法 进行 求 解 ，得 出各 阶段 的最 短 路径 ，最 终 求 出全 局 最 优解 ．与 以 往 算 法 相 比此 方 法 在 得 出全局最优解的同时 ，有效地减少 了计算量 ，整个分析求解过程简单明了． 2 动态规划算法 在 2O世 纪 5O年代 ，美 国数 学 家 贝 尔曼 (Richard Bellman)等 人根 据 多 阶段 决 策 问 题 的特 点 ，提 出 了“最 优性原理”，从 而创建了解决最优化问题 的一种方法一动态规划[4]．动态规划是求解多级决策过程最优化 的 一 种数学方法 ，所谓多级决策过程[5]，是指把一个过程分成若干阶段 ，每一阶段都要做出决策 。以使整个过 程取得最优效果．通过对 多级决策问题 的讨论 ，可以初步了解动态规划的思想和方法．最短路径 问题是多级 决 策 问题 的一个 典 型 例 子 ． 在机器人避障过程 中，通过其 中一个 障碍物之后到达 目标 点的路径是根据后续障碍物 的位置所确定 的．根据动态规划知识于是提 出了利用该算法对移动机器人路径规划的设计． 3 避 障路径规划 在可视图法 中，避 障的实质就是 当无法按照直线 到达 目标 时要绕过障碍物．根 据这样就可以将其看成 是 以求解过程中所遇到的障碍物为阶段 的多阶段决策问题 ，路径规划转 变成 了多 阶段决策 ，问题 的求解可 以用动态规划来实现． 所以按照动态规划的求解思路 ，首先规划求解环境 ，然后根据障碍物的分布把 问题划分为若干个阶 段 。接着对各阶段状态点 进行确定． 3．1 求解环境 可视图求解方法即为将所有的实际障碍物集合等效成平 面中的多边形集合 。并将起始点和 目标点在 空间中对应 的点扩充到多边形集合 中．将机器人的尺寸扩充到障碍物边界 ，使得机器人在求解环境 中可视 为一点 ，如图 1所示．另外 ，在等效 图中多边形 的凹处通过连接其顶点后使 之变成 凸多边形后 。这样可以减 少计算并且不会影响求解结果．所以可 以按这样 的方式来构建求解环境 ：将机 器人视为一点 。同时将 障碍 物等效成平面 中的凸多边形集合 ，并将起始点和 目标点在空间中对应 的点扩充到多边形 的集合 中． 3．2 阶段划分 根据路径 中所绕过 的障碍物的个数来划分 阶段数 ，通过对每一阶段都做出决策 ，以使整个过程取得最 优效果．如 图 1(a)所示 ，将障碍物 由起始点开始向 目标点按顺序分成 Ⅳ个 阶段． 当两个 障碍物并排时 ，或者是于坐标 图中做平行与 轴 的线 ，若此线能同时两个或两个 以上的障碍物 时，将这些障碍物看为同一个 阶段．如图 1(b)所示．其中 ，S为出发点 ，G为 目标点 ，I为第 1阶段 障碍物 ，Ⅱ 为第 2阶段障碍物． (a)障碍物的阶段划分 (b)障碍物并 行时 的阶段划分 图 1 障碍 物 的 阶 段 划分 图 2 各 阶 段 状 态 点 的确 定 

第 4期 张 昊等 ：基于动态规划算法的机器人避障路径研究 37 3．3 各 阶段中状态点 的确定 在对机器人路径规划 中各阶段状态点的确定即是对障碍物 (凸多边形)部分顶点 的确定．如图 2所示． 其 中， 为第 1阶段 障碍物的各个顶点 ， 为第 Ⅱ阶段障碍物的各个顶点 ，像 1，B3，c2这些点在最 短路径中并未起到作用 ，如果简单的把每一阶段 中障碍物 的所有顶点都确定为状 态点 的话 ，那么就会增加 许多不必要的计算． 因此 ，应当充分考虑实 际情况舍去不必要 的点来完成对状态点 的确定．通过对各种 图形 的研究 ，对 各 阶 段状 态 点 的确 定做 出 以下 规定 ： 1)以起始 点 为 源点 分 别 对各 个 障碍 物做 切 线 ，切 点必 为 状态 点 ．如 图 3(a)所示 ．确 定点 B1，B2，C1，c2． 2)以阶段 I为对象 ，以已确定 状态点向 目标点作直线 ，若 能直达 ，则将此边后续 已标记状态点省略．若 不 能直达 ，则不作任何处理．如 图 3(b)所示 ，阶段 I中状态点 2能直达 目标点 ，所 以舍去此边 已标记状态 点 C2． 3)以阶段 I为对象 ，以已确定状态点 向最后 阶段所标记状 态点作直 线 ，若能直达 ，则将此边后续 已标 记状态点省略．若不能直达 ，则不作任何处理．如图 3(c)所示 ，阶段 I中状态点 曰1，B2能直达阶段Ⅲ所标 记 状态点 ，所 以省略阶段 Ⅱ中已确定状态点．然后从最末状态往前依次进行处理． L“‘ 3 ≤ 、 ＼ 『) S(A) (a)以起始点向障碍物做切线 (b)以阶段 I为对象向 目标点做直线 (c)以已确定点 向下阶段状态点作直线 图 3 各 阶段 状 态 点 的确 定 4)对于相邻 两障碍物 ，如图 4所 示 ，判 断 已确 定 状态 点 B1，B2分 别 与 C1和 C2 ， 是否能够直线到达 ，如果能 ，则就不用再 去 确定其 他状态 点．如 图 4(a)；如果 不能 ，则 再判定其连线与凸多边形的哪条边相交[ 。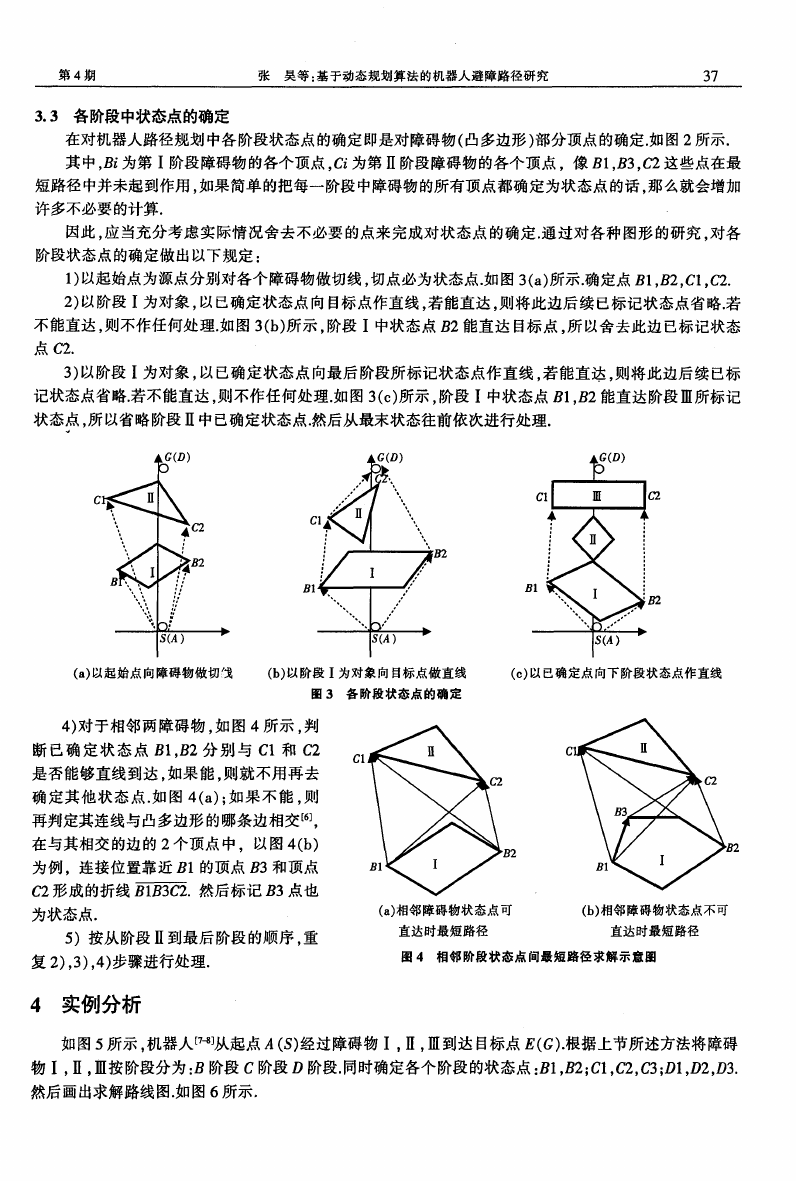 在与其相交 的边的 2个顶点中 ，以图 4(b) 为例 ，连接位置靠近 1的顶点 3和顶点 c2形 成 的折线 B1B3C2．然后 标 记 3点也 为状 态 点 ． 5)按从 阶段 Ⅱ到最后阶段 的顺 序 ，重 复 2)，3)，4)步骤进行处理． 4 实例分析 (a)相邻 障碍物状态点可 (b)相邻 障碍物状态点不可 直 达 时 最短 路 径 直 达 时最 短 路 径 图 4 相 邻 阶 段 状 态 点 问 最短 路径 求解 示 意 图 如图 5所示 。机器人[7--s]从起点 A(S)经过 障碍物 I，Ⅱ，Ⅲ到达 目标 点 E(G)．根据上节所述方法将障碍 物 I，Ⅱ，Ⅲ按 阶段分为 ：B阶段 C阶段 D阶段．同时确定各个 阶段 的状态点 ：B1，B2；C1，6'2，C3；D1，D2，D3． 然后画出求解路线 图．如 图 6所示． 

38 广西 工 学 院 学报 第 22卷 Ⅱ 图 5 机 器 人 可 行 路 线 图 图 6 求 解 路 线 图 4．1 动态规划求解过程 根据动态规划递推公式可将所求最短路径分为 4个小过程 ： N=4(D级)，从第 Ⅲ障碍物到 目标 的距 离分别为 ： = (D1)=2； =(D2)=8；Jl=(D3)=5； N=3(C级)，从第 Ⅱ障碍物到 目标 的距离分别为 ： j,(c1)=d(Cl，c2)+d(c2，D1) (D1)=8 Jl(C2)=d(C2，D1)+ (D1)=7 (C3)=d(C3，D1) (D1)=6 Ⅳ_2( 级 )，从第 1障碍物到 目标的距离分别为 ： 删 =mi ．7 (B2)=min d (B2 , C ={ )=9 ， I={；：兰】=7 1)+ Z( C1) … 一 ， … … … N=I(A级 )，从起始点到 目标 的最短距离为 ： Id(A，B1)+ (B1)I I2+9 I 五(A)=rain{d(A，B2)+J3(B2)}=min{2+7 f=9 Id(A，B3) (D2)j I7+8 J 所 以 ，可 以得 出最 短 距 离 为 9；最短 路 径 为 A 2一C3—Dl—E． 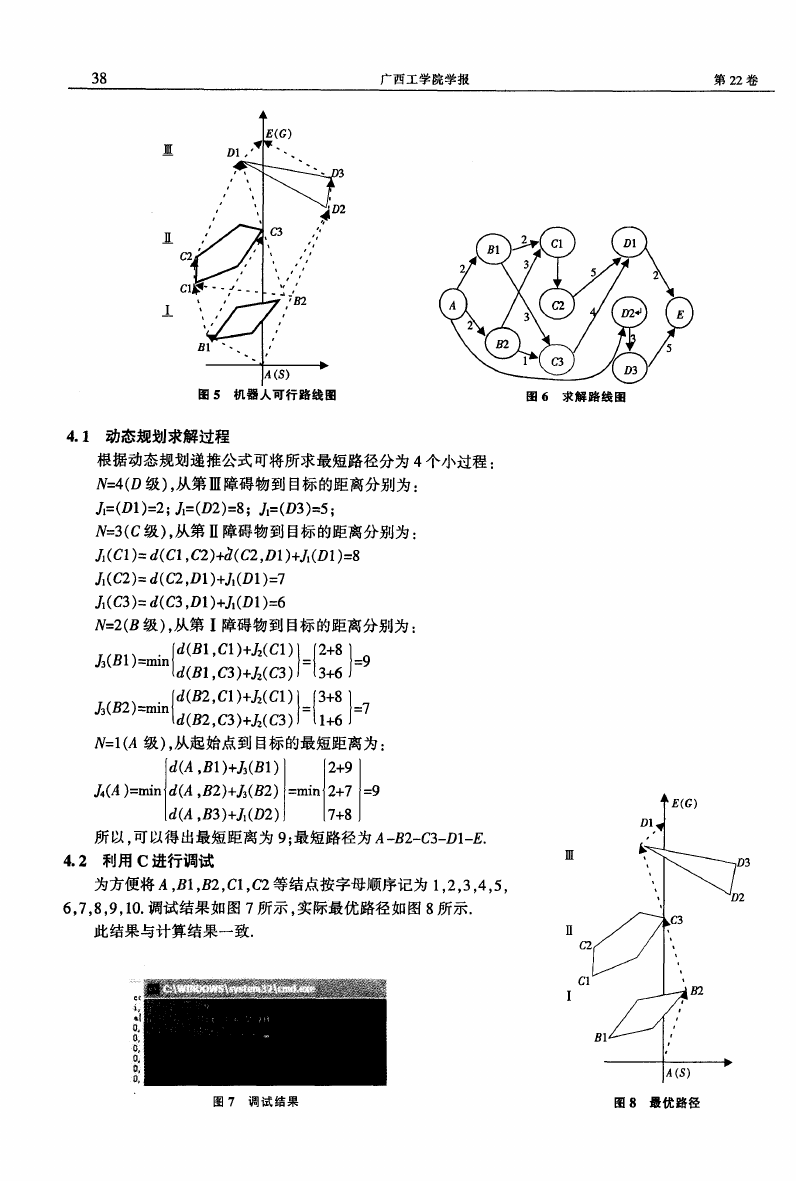4．2 利用 C进行调试 为方便将 A，B1，B2，C1，C2等结点按字母顺序记为 1，2，3，4，5， 6，7，8，9，10．调试结果如 图 7所示 ，实际最优路径如图 8所示． 此 结果 与 计 算结 果 一 致 ． Ⅲ Ⅱ C2 C1 瓴 m ＆ 图 7 调 试 结 果 图 8 最 优 路 径 

第 4期 张 昊 等 ：基 于 动 态规 划 算 法 的 机器 人 避 障 路 径研 究 39 5 结论 本文 以可视 图法所构建 的环境 为基础 ，根据动态规划 的知识 ，使蔽 障问题转化为多 阶段决策问题 ，最 后进行动态规划求出最终 的路径．这种分 阶段分层次的求解方法使复杂 的路径规划 问题得到了简化．在求 解 的过程 中对 可 视 图 进行 了改 进 ，在分 析多 种 情况 下 总 结 了对 各 阶 段 状态 点确 定 的有 效 方法 。从 而 减 少 了 计算量 ，并通过实例分析证 明了该方法 的可行性． 参 考 文 献 [1]戴光明．避障路径规划的算法研究 [D]．武汉 ：华中理工大学 ，2004． [2]孔峰 ，陶金 ，谢超平．移动机器人路径 规划技术研究 [J]．广西工学院学报 ，2009，20(4)：70．74． [3]Oommen B．，Iyengar S．，Rao N．，et a1．Robot navigation in unknown terrains using learned visibility graphs，part I： e disjoint convex obstacle case[J]．IEEEJournal ofRobo tics andAutomation，1987，3(6)：823．681． [4]胡寿松 ，王执铨 ，胡维礼．最优控制理论与系统[M]．北京 ：科学出版社 ，2005． [5]徐玖平 ，胡知能 ，王绥．运筹学 [M]．2版．北京 ：科学 出版社 ，2004． [6]az榕 ，李新国．高超声速飞行器水平航迹规划算法研 究[J]．计算机仿真 ，2008，25(11)：76．79． [7]蒋新松．机器人学导论 [M]．沈 阳：辽 宁科学技术 出版社 ，1994． [8]BergMarkde，KreveldMarc van，OvermarsMark，et a1．计 算几何算 法与应 用[M]．2版 ．邓俊辉 ，译 ．北京 ：清华大学出版社 ，2005： 338．348． Researches of Obstacle-avoiding Paths for Robots Based on the Dynamic Program mi ng Algorithm ZHANG Hao，LU0 Wen—guang，ZANG Qing-kai (Department of Electronic Information&Control Engineering，Guangxi University of Technology， Liuzhou 545006，China) Abstract：In order to simplify the complex path planning for mobile robots and to reduce the computation of feasible path，this thesis explores the path planning of obstacle avoidance in depth．Firstly this paper is based on the problem-solving environment of the visual graph，and transform s the path planning into a matter of multistage decision．Using the improved visual graph and geometry approximation algorithm，this paper solves each stage—problem and gets the shortest path of each stage．It has been pro ved by computer simulation results that the algorithm is correct，effi cient，practical and successfu1． Key words：obstacle—avoiding path planning；dynamic planning；visual gr aph；optimum paths (责任编辑 李捷 )