一种LED均匀照明矩形光斑透镜设计.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书资料大小：0.71M 资料格式：pdf 举报版权申诉

weixin_38570278-12132485-16359648075643322021.pdf-第1页.png

第1页 / 共9页

weixin_38570278-12132485-16359648075643322021.pdf-第2页.png

第2页 / 共9页

weixin_38570278-12132485-16359648075643322021.pdf-第3页.png

第3页 / 共9页

weixin_38570278-12132485-16359648075643322021.pdf-第4页.png

第4页 / 共9页

weixin_38570278-12132485-16359648075643322021.pdf-第5页.png

第5页 / 共9页

weixin_38570278-12132485-16359648075643322021.pdf-第6页.png

第6页 / 共9页

weixin_38570278-12132485-16359648075643322021.pdf-第7页.png

第7页 / 共9页

weixin_38570278-12132485-16359648075643322021.pdf-第8页.png

第8页 / 共9页

文本预览

中国科技论文在线 http://www.paper.edu.cn 一种 LED 均匀照明矩形光斑透镜设计 # 杨婷，尹韶辉，张营营** （湖南大学国家高效磨削工程技术研究中心，湖南长沙） 5 10 15 摘要：为了改善 LED 矩形光斑透镜的能源利用率、光斑均匀性和透镜表面平滑性，设计了一种均匀照明、光斑为矩形的透镜。在双极坐标系上对光源立体角进行非均匀划分，然后通过能量守恒原理，将矩形目标照明面划分成与光源立体角一一对应的梯形区域。结合 Snell 定理和切平面迭代法，建立透镜模型。并对透镜进行光线追踪仿真，结果表明：对于发光角度为 120 度的 LED 点光源，91.32%的能量集中在 800mm×600mm 的矩形光斑中，其中归一化照度均匀性达到 85%，相对标准偏差（RSD）为 0.416%。并且其透镜表面平滑，曲率变化平缓。因此在双极坐标上对光源进行非均匀网格划分，并将目标照明面划分成与光源立体角一一对应的梯形目标照明面元，有利于提高 LED 矩形光斑透镜的能源利用率、光斑均匀性和透镜表面平滑性。关键词：光学；非成像光学；发光二极管；矩形光斑中图分类号：O435 Design of Lens with Rectangular Light Spot for LED Uniform Illumination Yang Ting, Yin Shaohui, Zhang Yingying 20 (National Engineering Research Center for Hight Efficiency Grinding，Hunan University， Changsha，Hunan，China) Abstract: In order to improve energy efficiency, light distribution uniformity and lens surface smoothness of LED rectangular spot lens, a lens was designed, which with uniform illumination and a rectangular light distribution. The solid angle of light source is sampled in a double-polar coordinate system, and the target rectangular illumination surface is divided into a trapezoidal region corresponding to the solid angle of light source by the energy conservation principle. The lens model is obtained by Snell's theorem and tangent plane iteration method. The simulation results show that 91.32% energy is concentrated in the rectangular spot of 800mm×600mm for the LED spot light with the light emitting angle of 120 degrees, where the normalized illumination uniformity is 85% and the relative standard deviation is 0.416%. The lens surface is smooth and the curvature changes gently. Therefore, in the double-polar coordinate system, light source is split in a non-uniform grid and the target illumination surface is divided into a trapezoidal target illuminating surface block corresponding to the solid angle of light source, which is favorable to improve energy utilization ratio, light distribution uniformity and lens surface smoothness of LED rectangular spot lens. Key words: optical; non-imaging optics; light-emitting diodes; rectangular light spot 25 30 35 0 引言 LED 以光效高、寿命长、体积小、无污染、低耗能和易控制等优势被认为是最有可能替代白炽灯的第四代照明光源[1]。它广泛应用于道路照明、汽车车灯，投影照明和医疗照明基金项目：国际科技合作专项项目(2014DFG72480) 作者简介：杨婷（1992-），女，硕士研究生，主要研究方向：光学设计与模压仿真通信联系人：尹韶辉（1967-），男，博士，教授，主要研究方向：超精密加工. E-mail: shyin2000@126.com - 1 -

中国科技论文在线 http://www.paper.edu.cn 等[2]。然而，LED 是朗伯体光源，其光源分布为余弦分布，当其应用于道路照明等系统时， 40 照明区域的光斑通常要求为均匀矩形光斑，因此需要二次光学设计来产生均匀的矩形光斑[3]。 LED 矩形光斑透镜主要应用于两方面：一是应用在道路照明，医疗等领域对固定目标面均匀照明，要求直接生成均匀矩形光斑；二是应用在光斑形状很复杂的透镜，如汽车车灯，需要通过矩形光斑拼接成所需的光斑[4]。实现均匀矩形光斑的透镜设计方法有多种，具体可以归纳为三种，第一种 45 M-A(Monge-Ampère)数值解法，通过 Snell 定理和能量守恒原理得到带有边界条件的 Monge- Ampère 方程，通过牛顿迭代算法求解出自由曲面的离散面型数据[5]。M-A 方法计算结果准确，但是求解微分方程过程复杂。第二种为二次曲面包络法，由该方法得到的自由曲面是一个由有限个基于几何图形（抛物面、椭球面或笛卡尔卵圆面）组成的包络面[6]。二次包络面法它需要不断移动目标上的焦点进行优化。第三种为基于变量可分离映射关系的自由曲面设 50 计方法，即划分网格法[7]，它主要有辐射型、经纬型和双极坐标系型等三种网格划分法[2,7-8]。辐射型网格划分法在对角线上的照度明显高于其它区域，并且透镜表面不平缓；经纬型网格划分法易偏离于矩形；通用双极坐标系网格法的光斑均匀性较低，网格划分法产生的透镜都需要进一步的优化。本文在双极坐标系上将光源非均匀划分，根据能量守恒原理将目标照明面划分成梯形，从而建立了光源与目标照明面之间的拓扑关系。该拓扑关系改善了传统网格 55 划分法的光斑均匀性和透镜的光滑性，有利于简化均匀光斑矩形透镜的设计流程，减少优化时间，并便于透镜的加工。 1 设计方法 1.1 双极坐标系网格划分利用网格划分法设计自由曲面透镜的关键是确定网格拓扑关系，即光源立体角与目标照 60 明面之间的对应关系。它主要分为两步，第一步划分光源立体，第二步划分对应的目标照明面。本文在双极坐标系上对光源立体角进行非均匀网格划分。如图 1（a）所示，首先建立光源单位球，第一个极坐标系为 φ 和 θ 所在的坐标系，由 X 轴、Y 轴和 Z 轴组成，光源位于坐标系原点 O 点，Z 轴方向为主光线方向。其中，φ 为光线与 Z 轴的夹角，θ 为光线在 X-Y 平面上的投影与 X 轴之间的夹角。第二个极坐标系为 α 和 β 所在的坐标系，由 X´轴、 65 Y´轴和 Z´轴组成，坐标原点位于单位球最下方 O´。其中，α 为 Y-Z 平面与 O´A 与 O´X´所在的平面之间的夹角，β 为 X-Z 平面与 O´A 与 O´Y´所在的平面之间的夹角。令 A 为光源立体角单位球上任意一点，则 A 点的坐标（x，y，z）既可以用 φ 和 θ 表示，又可以用 α 和 β 坐标系来表示，如公式（1）所示。 - 2 -

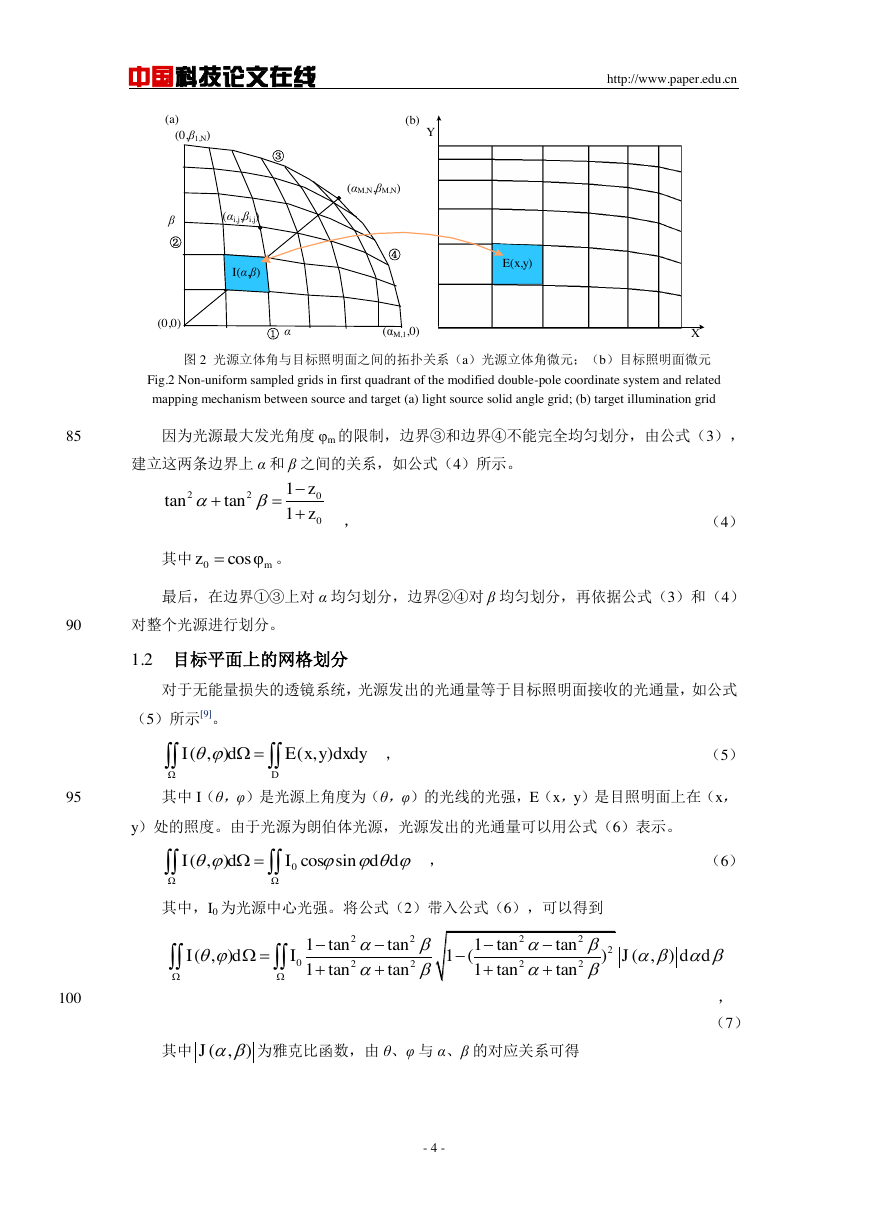
中国科技论文在线 http://www.paper.edu.cn 70 (b) 图 1 α-β 网格划分法。（a）双极坐标系示意图；（b）光源立体角网格划分效果图 Figure.1 α-β meshing method (a) diagram for the modified double-pole coordinate system; (b) diagram for the solid angle of light source ，（1） 75 可以得到 θ、φ 与 α、β 的对应关系，如公式（2）所示。，（2）由于整个光学系统为四分之一对称系统，因此只需要考虑光学系统的四分之一，在四分之一光源上插入 M×N 个点，将该四分之一光源划分成（M-1）×（N-1）份，如图 2 所示。令此光源最大发光半角为 φm，则可得到，四个顶点的 α 和 β，如公式（3）所示。 80 ，（3） - 3 - αYY´ X´ O´ X OA(a)βZ´ X´ Y´ （b）2222222222221tantansincos(1)tan1tantan1tantansinsin(1)tan 1tantan1tantancos1tantanxyz22221tantan=arccos1tantantanarctan()tan1,11,1M,11,NmmM,NM,Nm0,φ sinφarctan()2(1cosφ)

中国科技论文在线 http://www.paper.edu.cn 图 2 光源立体角与目标照明面之间的拓扑关系（a）光源立体角微元；（b）目标照明面微元 Fig.2 Non-uniform sampled grids in first quadrant of the modified double-pole coordinate system and related mapping mechanism between source and target (a) light source solid angle grid; (b) target illumination grid 85 因为光源最大发光角度 φm 的限制，边界③和边界④不能完全均匀划分，由公式（3），建立这两条边界上 α 和 β 之间的关系，如公式（4）所示。，（4）其中。最后，在边界①③上对 α 均匀划分，边界②④对 β 均匀划分，再依据公式（3）和（4） 90 对整个光源进行划分。 1.2 目标平面上的网格划分对于无能量损失的透镜系统，光源发出的光通量等于目标照明面接收的光通量，如公式（5）所示[9]。 95 其中 I（θ，φ）是光源上角度为（θ，φ）的光线的光强，E（x，y）是目照明面上在（x， y）处的照度。由于光源为朗伯体光源，光源发出的光通量可以用公式（6）表示。，（5）其中，I0 为光源中心光强。将公式（2）带入公式（6），可以得到， 100 其中为雅克比函数，由 θ、φ 与 α、β 的对应关系可得（6），（7） - 4 - X(αM,1,0) E(x,y)βα(0,0)(0,β1,N) (αM,N,βM,N) (αi,j,βi,j) ②①③④ I(α,β)Y(a)(b)22001ztantan1z0mzcosφΩD(,)d()IEx,ydxdy0ΩΩ(,)dcossinIIdd22222022221tantan1tantan(,)I1()(,)1tantan1tantanIdJdd(,)J

中国科技论文在线，则每个光源立体角的光通量为 Φi,j，如公式（9）所示： http://www.paper.edu.cn （8） 105 ，其中 dAi,j 格点光源的光源立体角，如公式（10）所示：（9），（10）根据能量守恒来求光源立体角和目标照明面之间的拓扑关系，由于这是均匀矩形照明，因此 E（x，y）为定值，令其为 E0。将目标照明面也划分成（M-1）×（N-1）份，目标照明 110 面在 X 轴的半长为 Lx，目标照明面在 Y 轴的半长为 Ly，如图 2 所示，先用 M 条直线，将目标照明面分成（M-1）份，由于目标照明面不可积性，采用微元法，可以得到第 m 条竖线和第 n 条横线的交点上的横坐标值：由于能量守恒，则每个光源立体角微元与每块目标照面微元的光通量相等，如公式（12），（11） 115 所示：，（12）其中 dA´i,j 目标照明面梯形微元的面积，可以得到第 m 条竖线和第 n 条横线的交点上的纵坐标值： 120 ，（13）由此可得第 m 条竖线和第 n 条横线的交点处的纵坐标值：，（14） - 5 - 22222secsec(,)tantanJ2222i,ji,ji,ji,j,,223i,ji,j4secsec(1tantan)(1tantan)1,2...,M;1,2...,N;ijijdAiji,ji,j1i1,ji1,j1i,ji1,ji,j1i1,j1,()()4ijdA,,,0 =1;N22 =2,3...,M;MN22ijijmnxijijmmdAxijLmdAij,,0,EijijijdAdA,1,,,11,1,1,(xx)(yyyy)2ijijijijijijijdA,,,11,11, ,0 =1;2222,3...,;ijijmnymnmnmnijijnndAyjLyyyNdAjnN

中国科技论文在线 http://www.paper.edu.cn 2 设计结果与分析 2.1 透镜结构根据上文建立的光源与目标照明面之间的拓扑关系，选择初始参量透镜内圆半径 125 r0=8mm，光源最大发光角度 φm=π/3；透镜初始厚度 Zs=20mm，目标照明面到点光源的距离 Zm=500mm，目标照明面在第一象限的端点坐标 Lx=400mm，Ly=300mm。结合公式（15） Snell 定理[9]和切平面迭代法[1]，得到如图 3 所示的透镜模型。并由观察得出，透镜外表面光滑，无曲率突变的地方。，（15） 130 图 3.透镜结构图 Figure.3 Lens structure diagram 其中 O 为出射光线单位向量，其中 In 为出射光线单位向量，Nf 为透镜外表面单位法向量，n1 为透镜周围介质的折射率，该介质通常为空气，空气的折射率是 1，n2 为透镜材料的 135 折射率，选用 BK7 玻璃，其折射率是 1.51680。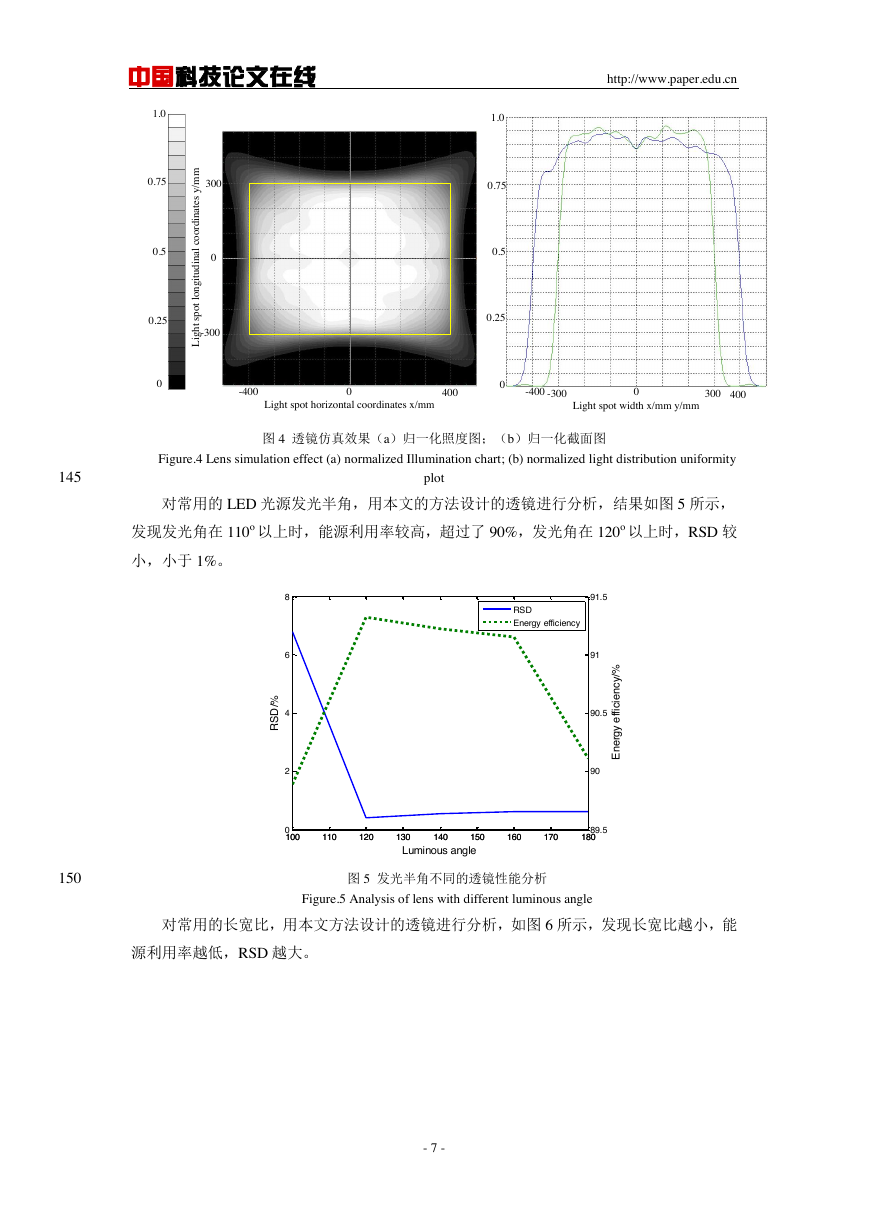 2.2 结果分析设置光源为点光源，将透镜导入 Tracepro 仿真软件中，用该软件对该透镜进行光线追踪。仿真结果如图 4 所示，光线基本在目标照明面内，能源利用率为 91.32%，均匀度在 85% 左右，经过计算，RSD 为 0.416%，透镜表面平缓。因而采用双极坐标系网格划分法相比于 140 辐射型网格划分法和经纬型网格划分法，透镜表面更加平缓，表面均匀性要更好，大大节省了后续的优化过程。 - 6 - 1/222121212n-n=n+n-2nn()nnfOIOIN24.6mm28.1mm

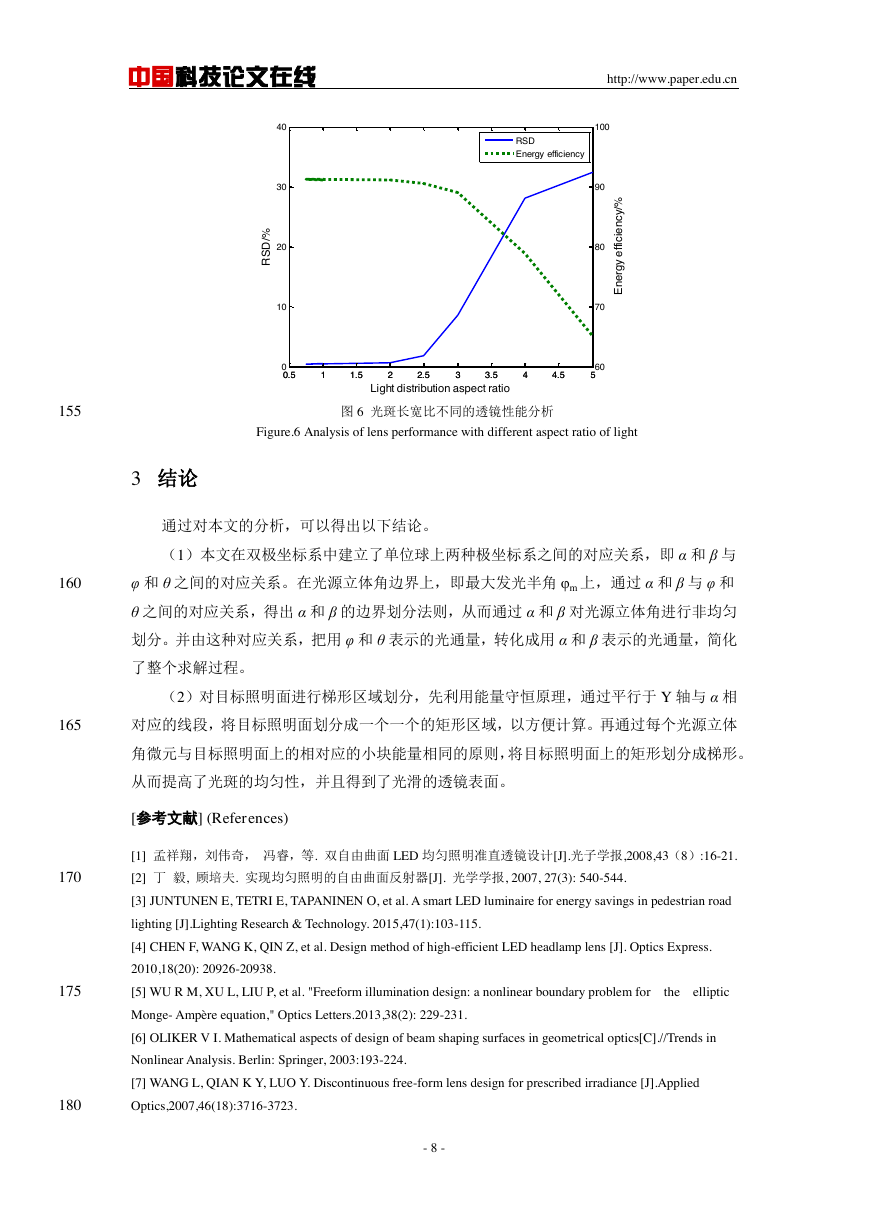
中国科技论文在线 http://www.paper.edu.cn 图 4 透镜仿真效果（a）归一化照度图；（b）归一化截面图 Figure.4 Lens simulation effect (a) normalized Illumination chart; (b) normalized light distribution uniformity 145 plot 对常用的 LED 光源发光半角，用本文的方法设计的透镜进行分析，结果如图 5 所示，发现发光角在 110o 以上时，能源利用率较高，超过了 90%，发光角在 120o 以上时，RSD 较小，小于 1%。 150 图 5 发光半角不同的透镜性能分析 Figure.5 Analysis of lens with different luminous angle 对常用的长宽比，用本文方法设计的透镜进行分析，如图 6 所示，发现长宽比越小，能源利用率越低，RSD 越大。 - 7 - 0-400400-3000300（a）1.00.500.250.75Light spot longitudinal coordinates y/mmLight spot horizontal coordinates x/mm00.51.00.250.750-400-300400300Light spot width x/mm y/mm10011012013014015016017018002468RSD/%Luminous angle 10011012013014015016017018089.59090.59191.5Energy efficiency/%RSDEnergy efficiency

中国科技论文在线 http://www.paper.edu.cn 155 图 6 光斑长宽比不同的透镜性能分析 Figure.6 Analysis of lens performance with different aspect ratio of light 3 结论通过对本文的分析，可以得出以下结论。（1）本文在双极坐标系中建立了单位球上两种极坐标系之间的对应关系，即 α 和 β 与 160 φ 和 θ 之间的对应关系。在光源立体角边界上，即最大发光半角 φm 上，通过 α 和 β 与 φ 和 θ 之间的对应关系，得出 α 和 β 的边界划分法则，从而通过 α 和 β 对光源立体角进行非均匀划分。并由这种对应关系，把用 φ 和 θ 表示的光通量，转化成用 α 和 β 表示的光通量，简化了整个求解过程。（2）对目标照明面进行梯形区域划分，先利用能量守恒原理，通过平行于 Y 轴与 α 相 165 对应的线段，将目标照明面划分成一个一个的矩形区域，以方便计算。再通过每个光源立体角微元与目标照明面上的相对应的小块能量相同的原则，将目标照明面上的矩形划分成梯形。从而提高了光斑的均匀性，并且得到了光滑的透镜表面。 [参考文献] (References) [1] 孟祥翔，刘伟奇，冯睿，等. 双自由曲面 LED 均匀照明准直透镜设计[J].光子学报,2008,43（8）:16-21. 170 [2] 丁毅, 顾培夫. 实现均匀照明的自由曲面反射器[J]. 光学学报, 2007, 27(3): 540-544. [3] JUNTUNEN E, TETRI E, TAPANINEN O, et al. A smart LED luminaire for energy savings in pedestrian road lighting [J].Lighting Research & Technology. 2015,47(1):103-115. [4] CHEN F, WANG K, QIN Z, et al. Design method of high-efficient LED headlamp lens [J]. Optics Express. 2010,18(20): 20926-20938. 175 [5] WU R M, XU L, LIU P, et al. "Freeform illumination design: a nonlinear boundary problem for the elliptic Monge- Ampère equation," Optics Letters.2013,38(2): 229-231. [6] OLIKER V I. Mathematical aspects of design of beam shaping surfaces in geometrical optics[C].//Trends in Nonlinear Analysis. Berlin: Springer, 2003:193-224. [7] WANG L, QIAN K Y, LUO Y. Discontinuous free-form lens design for prescribed irradiance [J].Applied 180 Optics,2007,46(18):3716-3723. - 8 - 0.511.522.533.544.55010203040RSD/%Light distribution aspect ratio 0.511.522.533.544.5560708090100Energy efficiency/%RSDEnergy efficiency

分享到：

赞收藏

资料库

一种LED均匀照明矩形光斑透镜设计.pdf

相关推荐

开发技术

热门标签

最新资料