FCM算法中参数的优选方法及实例应用.pdf-资料库

mushangege-3304590-4744302543306479258.pdf-第1页.png

第1页 / 共25页

mushangege-3304590-4744302543306479258.pdf-第2页.png

第2页 / 共25页

mushangege-3304590-4744302543306479258.pdf-第3页.png

第3页 / 共25页

mushangege-3304590-4744302543306479258.pdf-第4页.png

第4页 / 共25页

mushangege-3304590-4744302543306479258.pdf-第5页.png

第5页 / 共25页

mushangege-3304590-4744302543306479258.pdf-第6页.png

第6页 / 共25页

mushangege-3304590-4744302543306479258.pdf-第7页.png

第7页 / 共25页

mushangege-3304590-4744302543306479258.pdf-第8页.png

第8页 / 共25页

FCM 算法中参数的优选方法及实例应用 by faruto Email:faruto@163.com - 1 -

FCM 算法中参数的优选方法及实例应用摘要：本文在原始的 fcm 算法基础上，对算法中的聚类数 c 和加权指数 m 给出优选方法，进而而出了 fcm 参数优选自适应算法，通过人造数据与具有实际背景的数据验证可以看出该算法是有效的，该算法不但可以自适应的给出最佳的聚类数，而且可以验证聚类的有效性，达到最佳聚类的目的。关键字：FCM，聚类分析，聚类数，加权指数，自适应 Abstract：This paper gives a method of the optimal choice for fuzzy weighting exponent m and the numbers c. Then the Fuzzy c-Means clustering algorithm with parameters self-adepted is presented in this paper. At last expermental results with artificial data and data based on actual background illustrates the effectiveness of the algorithm. Keywords：FCM(Fuzzy C-Means algorithm)，fuzzy clustering analysis，cluster number，fuzzy weighting exponent，self-adepting - 2 -

内容目录第一章引论及FCM算法介绍----------------------------------------------------------- - 4 - 1.1 简介聚类分析--------------------------------------------------------------------------------- - 4 - 1.2 FCM算法介绍--------------------------------------------------------------------------------- - 4 - 1.2.1 普通（硬）－Ｃ均值聚类算法----------------------------------------------------------------- 4 - 1.2.2 模糊（软）－Ｃ均值聚类算法----------------------------------------------------------------- 5 - 1.3 聚类数c的研究 ------------------------------------------------------------------------------- - 7 - 1.4 加权指数m的研究及m对FCM算法的影响--------------------------------------------- - 8 - 第二章 FCM参数的优选自适应方法-------------------------------------------------- - 9 - 2.1 引言--------------------------------------------------------------------------------------------- - 9 - 2.2 聚类数c的自适应方法 ---------------------------------------------------------------------- 10 - 2.3 加权指数m的优选方法 --------------------------------------------------------------------- 12 - 2.3.1 c 划分模糊度 ----------------------------------------------------------------------------------- - 12 - 2.3.2 FCM中参数m的优选 -------------------------------------------------------------------------- - 14 - 第三章 FCM参数自适应算法的实例应用-------------------------------------------- 15 - 附录------------------------------------------------------------------------------------------- 20 - 参考文献------------------------------------------------------------------------------------- 25 - - 3 -

第一章引论及 FCM 算法介绍 1.1 简介聚类分析聚类就是按照事物间的相似性进行区分和分类的过程，它是一种无监督的分类。聚类分析则是用数学方法研究和处理所给定对象的分类。聚类是一个古老的问题，它伴随着人类社会的产生和发展而不断深化，人类要认识世界就必须区别不同的食物并认识事物间的相似性。传统的聚类分析是一种硬划分，它把每个待识别的对象严格地划分到某个类中，具有非此即彼的性质，这种分类的类别界限是分明的。随着人们认识的深入，发现这种分类越来越不适用于具有模糊性的问题，即那些并没有严格的属性的对象，它们在形态和类属方面存在着中介性，适合进行软划分。Zadeh 提出的模糊集理论为这种软划分提供了有力的分析工具，人们开始用模糊的方法来处理聚类问题，并称为模糊聚类分析。由于模糊聚类得到了样本数与各个类别的不确定性程度，表达了样本类属的中介性，即建立起了样本对于类别的不确定性的描述，能更客观地反映现实世界，从而成为聚类分析研究的主流。模糊划分的概念最早由 Ruspini 提出，利用这一概念人们提出了多种聚类方法，比较典型的有：基于相似性关系和模糊关系的方法（包括聚合法和分类法）、基于模糊等价关系的传递闭包方法、基于模糊图论最大树方法，以及基于数据集的凸分解、动态规划和难以辨识关系等方法。然而由于上述方法不适用于大数据量情况，难以满足实时性要求高的场合，因此其实际的应用不够广泛，故在该方面的研究也就逐步减少了。实际中受到普遍欢迎的是基于目标函数的方法，该方法设计简单。解决问题的范围广，最终还可以转化为优化问题而借助经典数学的非线性规划理论求解，并易于计算机实现。因此，随着计算机的应用和发展，该类方法成为聚类研究的热点[2,3]。 1.2 FCM 算法介绍 1.2.1 普通（硬）－Ｃ均值聚类算法普通（硬）－均值聚类（HCM）算法是经典的硬聚类算法之一，能够对超椭球状的 c 数据进行分类。 x x { , 1 2 X = 设 ,..., x n } s R ⊂ ，其中 x i = [ x i 1 , x 2 i ,..., x si ]T s R ∈ 是数据集，n 是数据集中元素的个数，c 是聚类中心数 jv ≤ ≤ iju 。是第 (1 ∈ R j c ) s j 个样本到第i 个聚类中心的隶属度， U u [ = ]ij c n × V ， = [ v ]ij s c × 。 ( c <<1 )n ， d ij = x j − v i jx 是样本和聚类中心的欧氏距离， iv 普通（硬）－Ｃ均值聚类问题可表示成下面的数学规划问题问题 HCL： - 4 -

目标函数： min J U c , ) 1 ( c n = ∑∑ i 1 = j 1 = u d ij 2 ij 约束条件： ≤ ≤ j n ,1 ≤ ≤ i c c = u ij 1,1 ⎧ ∑ ⎪ ⎪⎪ i 1 = u {0,1},1 ∈ ⎨ ij ⎪ n ∑ ⎪ < 0 ⎪⎩ u ij < 1 = j ≤ ≤ j n n ,1 ≤ ≤ i c 上述数学规划问题可由如下算法来求解：算法 HCM： STEP 0. 给出迭代标准 0ε> ，初始分类矩阵 (0)V 0=k ; ， STEP 1. 用下述公式计算 )kU ( ) u k ( ij STEP 2. 用下述公式计算 ( kV + 1) ) k d 1, ( ⎧ ⎪= ⎨ ij else 0, ⎪⎩ = min r c 1 ≤ ≤ ) d k ( rj k 1) + v ( i = u x k ( ) ij j n ∑ j 1 = n ∑ j 1 = ) u k ( ij STEP 3. 用一个矩阵范数 • 比较 ( kV + 1) )kV ( 与，若 V ( k 1) + − V ( k ) ≤ ε 则停止迭代，否则置 k=k+1, 转向 STEP 1。上述方法也可以用初始化划分矩阵 (0)U 来作为起始条件。 1.2.2 模糊（软）－Ｃ均值聚类算法 Dunn 依据 Ruspini 定义的集合的模糊划分概念，将普通（硬）－Ｃ均值聚类算法推广到模糊情形，如果不给隶属度乘一个权重，这种推广是无效的。而最简单和最直接的方 iju 法是将变成，由此 Dunn 给出现面的模糊（软）－Ｃ均值聚类数学规划问题： iju iju 2 - 5 -

目标函数： min J U c , ) 2 ( c n = ∑∑ i 1 = j 1 = u d 2 ij 2 ij 约束条件： c = u ij 1,1 ⎧ ∑ ⎪ ⎪⎪ i 1 = u [0,1],1 ∈ ⎨ ij ⎪ n ∑ ⎪ < 0 ⎪⎩ u ij < 1 = j ≤ ≤ j n ≤ ≤ j n ,1 ≤ ≤ i c n ,1 ≤ ≤ i c Bezdek 将上述表达推广到更一般的情形，给出模糊聚类的一般描述。模糊聚类问题可表示成下面数学规划问题[4] 问题 FCL：目标函数： min J U c , ) m ( c n = ∑∑ j u d m i 2 ij i 1 = j 1 = 约束条件： c = 1,1 ⎧ ∑ u ⎪ ij ⎪⎪ ∈ i 1 = u [0,1],1 ⎨ ij ⎪ n ∑ ⎪ < 0 ⎪⎩ u ij < 1 = j ≤ ≤ j n ≤ ≤ j n ,1 ≤ ≤ i c n ,1 ≤ ≤ i c 这里 m 是权重因子(m>1)，Bezdek 给出如下算法来解上述的数学规划问题。算法 FCM： STEP 0. 给出迭代标准 0ε> ，初始分类矩阵 0=k (0)V ， ; STEP 1. 用下述公式计算 )kU ( u k ( ) ij = 1 d k ( ) ij d k ( ) rj ( 2 m 1 − ) c ∑ r 1 = 如果存在 j,r,使得 rjd ( )k =0，则令： iju ( ) 1 k = i r u≠ , k ( ) ij 0 = 且对 STEP 2. 用下述公式计算 ( kV + 1) n ∑ j 1 = n k 1) + v ( i = u ( ) k m ( ) ij x j ∑ j 1 = u ( ) k m ( ) ij STEP 3. 用一个矩阵范数 • 比较 ( kV + 1) )kV ( 与，若 - 6 -

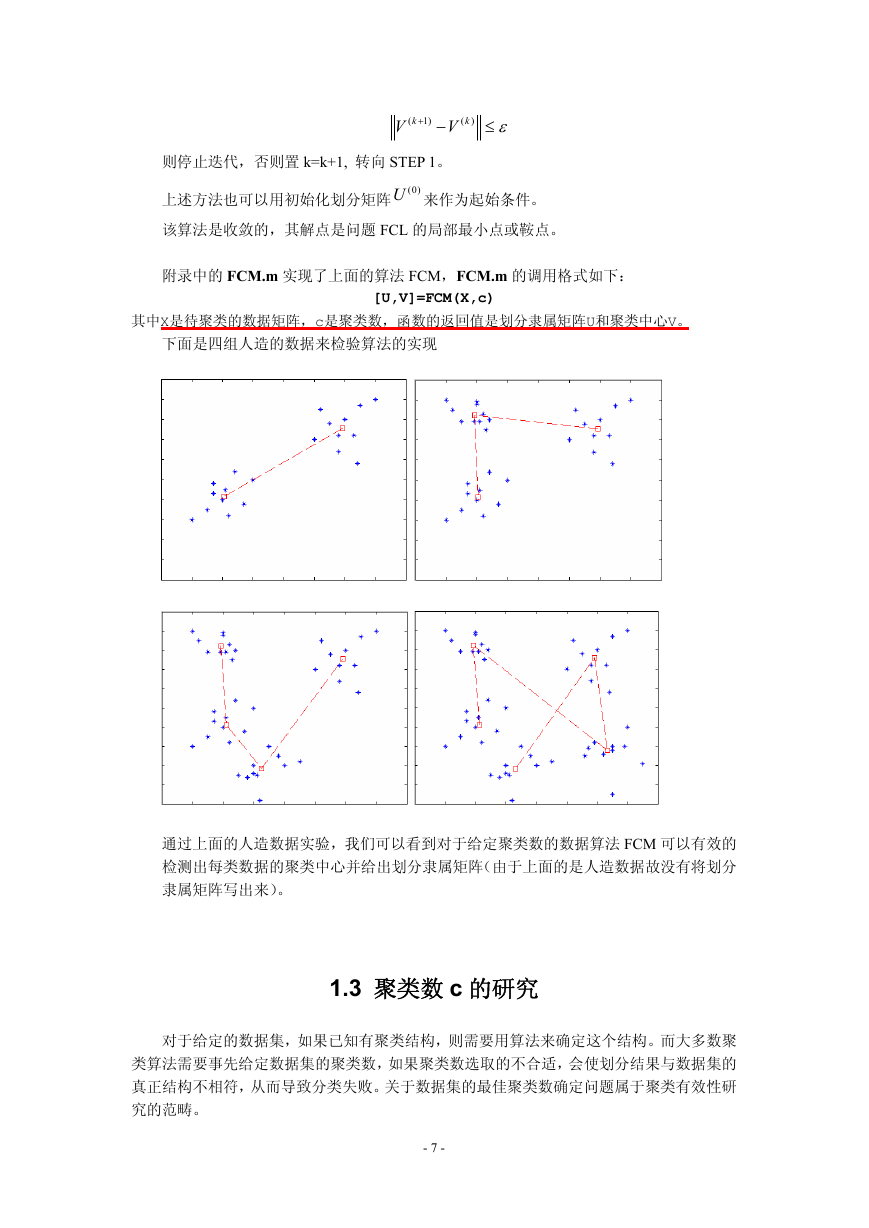
V ( k 1) + − V ( k ) ≤ ε 则停止迭代，否则置 k=k+1, 转向 STEP 1。上述方法也可以用初始化划分矩阵 (0)U 来作为起始条件。该算法是收敛的，其解点是问题 FCL 的局部最小点或鞍点。附录中的 FCM.m 实现了上面的算法 FCM，FCM.m 的调用格式如下： [U,V]=FCM(X,c) 其中X是待聚类的数据矩阵，c是聚类数，函数的返回值是划分隶属矩阵U和聚类中心V。下面是四组人造的数据来检验算法的实现通过上面的人造数据实验，我们可以看到对于给定聚类数的数据算法 FCM 可以有效的检测出每类数据的聚类中心并给出划分隶属矩阵（由于上面的是人造数据故没有将划分隶属矩阵写出来）。 1.3 聚类数 c 的研究对于给定的数据集，如果已知有聚类结构，则需要用算法来确定这个结构。而大多数聚类算法需要事先给定数据集的聚类数，如果聚类数选取的不合适，会使划分结果与数据集的真正结构不相符，从而导致分类失败。关于数据集的最佳聚类数确定问题属于聚类有效性研究的范畴。 - 7 -

关于聚类有效性问题的研究可分为以下三种研究途径。（1）基于数据集的模糊划分这类方法基于这样的观点，一个能较好分类的数据集应该是较“分明”的。因此，模糊划分的模糊性越小，聚类的结果越可靠。基于这种观点的第一个聚类有效性函数是由 Zadeh 提出的分离度，但正如 Bezdek 指出的，分离度并不能用。1974 年 Bezdek 借助 Dunn 提出的划分系数概念，提出了第一个实用的模糊聚西安电子科技大学硕士论文：FCM 参数研究及其应用类有效性函数并提出了与划分系数密切相关的另一个聚类有效性函数—划分熵。 Windham 利用隶属度的最大值定义了比例系数，Gunderson 利用划分系数成功地对星云域数据进行了分析，从而确立了这类方法的地位。1998 年 Trauwaert 分析指出划分系数的最大值并非总是对应最好的分类，这说明划分系数也具有很大的局限性。范九伦等用可能性分布的观点解释划分系数，提出了一个新的有效性函数，其性能明显地优于划分系数。（2）基于数据集的几何结构这类方法建立在这样的观点之上，一个能较好分类的数据集，每一个子类应该是紧致的并且子类与子类应尽可能分离的，以紧致性和分离性的比值作为聚类有效性标准。对于紧致性和分离性定义的不同，产生了不同的公式。应用数据集本身的特征，Dunn 定义了分离性指标并证明了该分离性指标大于 1 时，数据集具有唯一的聚类结构。，Gunderson 定义了分离系数。1979 年 Davics 和 Bouldin 利用类与类间的 Fisher 距离定义了分离性测度。基于数据集的模糊 C-均值聚类 Gath 和 Geva 引入了模糊超体积和模糊密度的概念，定义了与数据集结构非常密切的聚类有效性函数。1991 年 Xie 和 Beni 利用目标函数定义了一个称之为 Xie-Beni 指标的聚类有效性函数。（3）基于数据集的统计信息这类方法是基于硬聚类提出的，他们建立在这样的观点上，最佳分类对应的数据结构所提供的统计信息是最好的。基于数据集的类内统计信息和类间统计信息，Vogel 和 Wong 提出了 PFS 聚类方法。Jain 和 Moream 借助统计中的 Bootstrap 技术确定聚类有效性。基于信息论中的 AIC 准则，Zhang 和 Modestino 定义了一个聚类有效性函数。1992 年 Beni 和 Liu 基于最大熵原则提出了一种无偏差聚类算法和熵形式的聚类有效性函数。1997 年 Roberts 运用最大相关原则和标量空间滤波技术提出了一个聚类有效性函数。基于数据集模糊划分的有效性函数具有简单、运算量小的优点，但与数据集的结构特征缺少直接联系；基于数据集的几何结构的有效性函数也数据集的结构密切相关，但表述较复杂，运算量较大；基于统计信息的有效性函数的性能与数据集分布密切相关，但依赖于数据分布与统计假设的一致性。以上三种途径是聚类有效性问题研究的主流。目前聚类有效性问题的研究范围已拓广到椭球状、线状和壳状数据，还提出了基于可能性的聚类有效性函数。此外，也提出了一些针对噪声数据有效性函数。不过球状分布数据的模糊分类问题是最基本的，因为这类问题的研究结果可直接推广到其它数据的分析上。有效性问题是聚类分析的瓶颈，该问题的解决将会对聚类分析的成功应用产生十分深远的影响。 1.4 加权指数 m 的研究及 m 对 FCM 算法的影响 m< < ∞} { :1mJ 在模糊聚类目标函数中，Bezdek 引入了加权指数 m，使 Dunn 的聚类准则变成 m=2 的特例。有人认为从数学上看参数 m 的出现不自然也没有必要，但是对于从硬聚类准则函数推广到目标函数，如果不给隶属度乘一个权重，这种推广则是无效的。参数 m 又称为平滑因子，控制着模式在模糊类间的分享程度，因此要实现模糊聚类就必须选定一 - 8 -

资料库

FCM算法中参数的优选方法及实例应用.pdf

相关推荐

开发技术

热门标签

最新资料