第1页 / 共9页
第2页 / 共9页
第3页 / 共9页
第4页 / 共9页
第5页 / 共9页
第6页 / 共9页
第7页 / 共9页
第8页 / 共9页
GPS位置+速度两个观测量卡尔曼惯导航融合（无名创新）.pdf
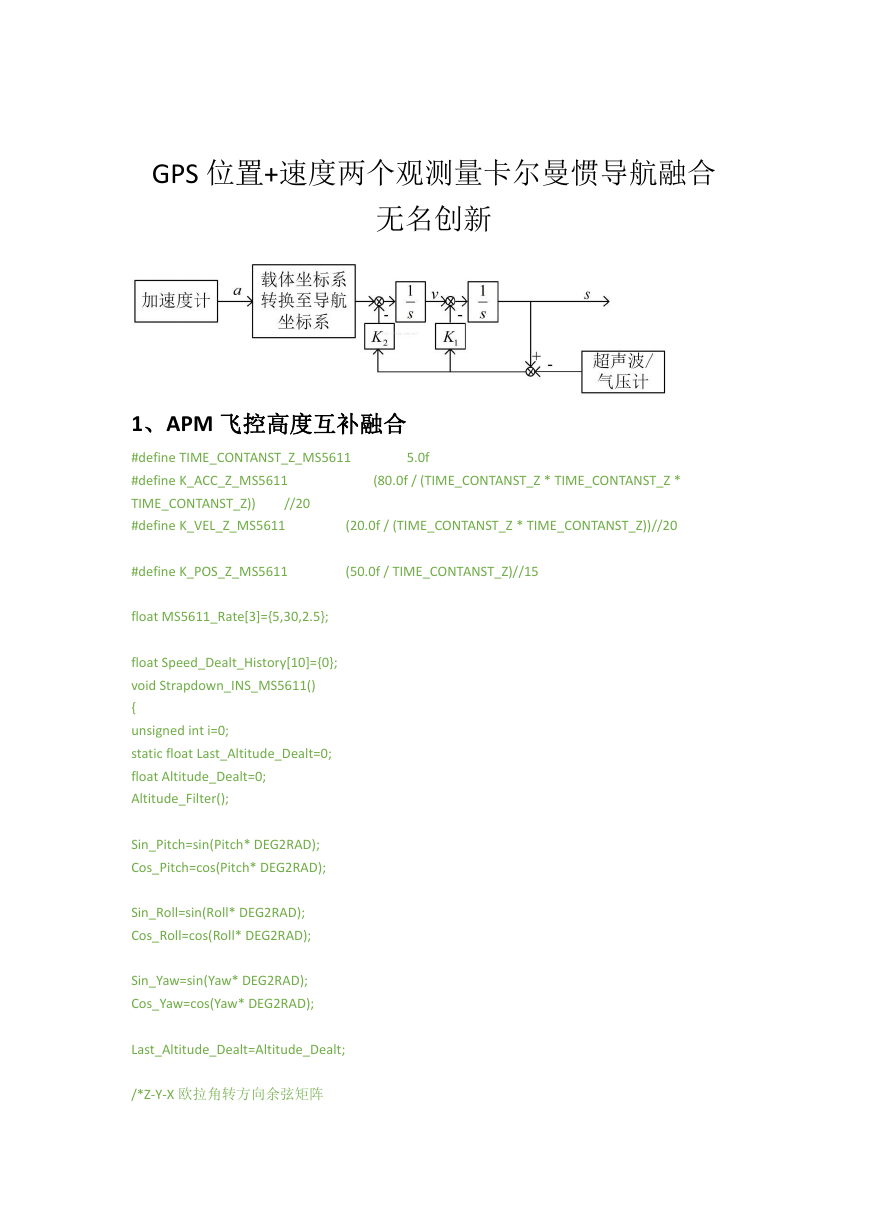
GPS 位置+速度两个观测量卡尔曼惯导航融合
无名创新
5.0f
(80.0f / (TIME_CONTANST_Z * TIME_CONTANST_Z *
(20.0f / (TIME_CONTANST_Z * TIME_CONTANST_Z))//20
1、APM 飞控高度互补融合
#define TIME_CONTANST_Z_MS5611
#define K_ACC_Z_MS5611
TIME_CONTANST_Z))
#define K_VEL_Z_MS5611
//20
#define K_POS_Z_MS5611
(50.0f / TIME_CONTANST_Z)//15
float MS5611_Rate[3]={5,30,2.5};
float Speed_Dealt_History[10]={0};
void Strapdown_INS_MS5611()
{
unsigned int i=0;
static float Last_Altitude_Dealt=0;
float Altitude_Dealt=0;
Altitude_Filter();
Sin_Pitch=sin(Pitch* DEG2RAD);
Cos_Pitch=cos(Pitch* DEG2RAD);
Sin_Roll=sin(Roll* DEG2RAD);
Cos_Roll=cos(Roll* DEG2RAD);
Sin_Yaw=sin(Yaw* DEG2RAD);
Cos_Yaw=cos(Yaw* DEG2RAD);
Last_Altitude_Dealt=Altitude_Dealt;
/*Z-Y-X 欧拉角转方向余弦矩阵
//Pitch Roll
Yaw 分别对应Φ θ Ψ
X 轴旋转矩阵
R（Φ）
{1
{0
{0
0
cosΦ
-sinΦ
}
0
sinΦ}
cosΦ }
Y 轴旋转矩阵
R（θ）
0
1
0
{cosθ
{0
{sinθ
Z 轴旋转矩阵
R（θ）
{cosΨ
{-sinΨ
{0
sinΨ
cosΨ
0
由 Z-Y-X 顺规有:
-sinθ}
0
cosθ}
}
0}
0}
1 }
载体坐标系到导航坐标系下旋转矩阵 R(b2n)
R(b2n) =R(Ψ)^T*R(θ)^T*R(Φ)^T
R=
{cosΨ*cosθ
{cosθ*sinΦ
{-sinθ
-cosΦ*sinΨ+sinΦ*sinθ*cosΨ
cosΦ*cosΨ +sinΦ*sinθ*sinΨ
cosθsin Φ
sinΨ*sinΦ+cosΦ*sinθ*cosΨ}
-cosΨ*sinΦ+cosΦ*sinθ*sinΨ}
cosθcosΦ
}
*/
Origion_NamelessQuad.Acceleration[_YAW] =
-Sin_Roll* X_g_av
+ Sin_Pitch *Cos_Roll * Y_g_av
+ Cos_Pitch * Cos_Roll * Z_g_av;//Z-Y-X 顺规旋转矩阵第三行-------
加速度载体到导航系
Origion_NamelessQuad.Acceleration[_YAW]*=AcceGravity/AcceMax;
Origion_NamelessQuad.Acceleration[_YAW]-=AcceGravity;
Origion_NamelessQuad.Acceleration[_YAW]*=100;//加速度 cm/s^2
//Altitude_Dealt=AirPresure_Altitude-NamelessQuad.Position[_YAW];//气压计(超声波)与 SINS 估计
量的差，单位 cm
Altitude_Dealt=Altitude_Estimate-NamelessQuad.Position[_YAW];//气压计(超声波)与 SINS 估计量的
差，单位 cm
for(i=9;i>0;i--)
{
Speed_Dealt_History[i]=Speed_Dealt_History[i-1];
}
Speed_Dealt_History[0]=Altitude_Dealt-Last_Altitude_Dealt;
acc_correction[_YAW] += MS5611_Rate[0]*Altitude_Dealt* K_ACC_Z_MS5611*CNTLCYCLE ;//加速度
校正量
vel_correction[_YAW] += MS5611_Rate[1]*Altitude_Dealt* K_VEL_Z_MS5611*CNTLCYCLE ;//速度校
正量
pos_correction[_YAW] += MS5611_Rate[2]*Altitude_Dealt* K_POS_Z_MS5611*CNTLCYCLE ;//位置校
正量
NamelessQuad.Acceleration[_YAW]=Origion_NamelessQuad.Acceleration[_YAW]+acc_correction[_YA
W];//加速度更新
SpeedDealt[_YAW]=NamelessQuad.Acceleration[_YAW]*CNTLCYCLE;//速度增量更新
Origion_NamelessQuad.Position[_YAW]+=(NamelessQuad.Speed[_YAW]+0.5*SpeedDealt[_YAW])*CN
TLCYCLE;//位置惯导更新
NamelessQuad.Position[_YAW]=Origion_NamelessQuad.Position[_YAW]+pos_correction[_YAW];//位
置校正更新
Origion_NamelessQuad.Speed[_YAW]+=SpeedDealt[_YAW];//速度惯导更新
NamelessQuad.Speed[_YAW]=Origion_NamelessQuad.Speed[_YAW]+vel_correction[_YAW];//速度校
正更新
}
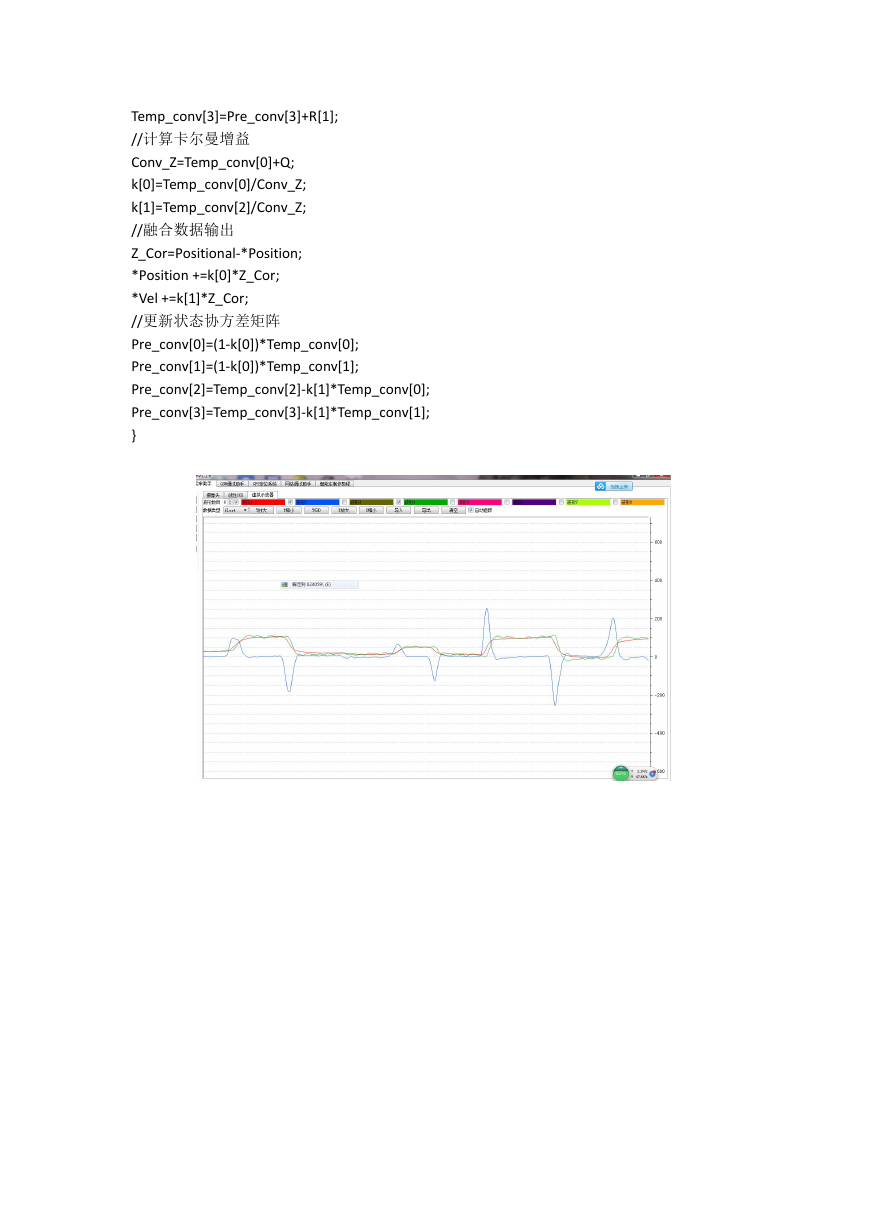
2、高度气压计、超声波单观测量卡尔曼滤波
KalmanFilter(float Positional,float *Position,float *Vel,float *Acce,float *R,float Q,float
0.004
#define Dt
float High_Position=0,Last_High_Position=0;
float High_Vel=0,Last_High_Vel=0;
float High_Acce=0,Last_High_acce=0;
float R[2]={7.47e-7f,3.0000001e-6f};
float Q=0.3;//0.01;
void
dt)
{
float Temp_conv[4]={0};//先验协方差
static float Pre_conv[4]={0};//上一次协方差
float Conv_Z=0,Z_Cor=0;
float k[2]={0};//增益矩阵
float Ctemp=0;
Ctemp=Pre_conv[1];
//先验状态
*Position +=*Vel*dt+(*Acce*dt*dt)/2.0;
*Vel+=*Acce*dt;
//先验协方差
Ctemp=Pre_conv[1]+Pre_conv[3]*dt;
Temp_conv[0]=Pre_conv[0]+Pre_conv[2]*dt+Ctemp*dt+R[0];
Temp_conv[1]=Ctemp;
Temp_conv[2]=Pre_conv[2]+Pre_conv[3]*dt;;
Temp_conv[3]=Pre_conv[3]+R[1];
//计算卡尔曼增益
Conv_Z=Temp_conv[0]+Q;
k[0]=Temp_conv[0]/Conv_Z;
k[1]=Temp_conv[2]/Conv_Z;
//融合数据输出
Z_Cor=Positional-*Position;
*Position +=k[0]*Z_Cor;
*Vel +=k[1]*Z_Cor;
//更新状态协方差矩阵
Pre_conv[0]=(1-k[0])*Temp_conv[0];
Pre_conv[1]=(1-k[0])*Temp_conv[1];
Pre_conv[2]=Temp_conv[2]-k[1]*Temp_conv[0];
Pre_conv[3]=Temp_conv[3]-k[1]*Temp_conv[1];
}
3、GPS 水平位置、速度双观测量卡尔曼滤波融合
状态变量:y 位移，v 速度
x
]T
y
[
v
状态先验更新方程：
x
[
k
1
0
dt y
][ ]
k
1
v
[
1
1
2
2
dt
dt
]
a
k
过程噪声：
R
[
0
r
0
0
]
1
r
观测方程：
z Hx H
y
[ ]
v
,其中观测量为状态全观测，故
H E
[
1 0
]
0 1
观测噪声：
Q
[
0
q
0
0
]
1
q
观测方程：
x
x
k
(
K z
k
k
，其中 kK 为 2 阶方阵：
x
)
k
K
k
[
k
k
0
2
1
k
]
3
k
状态协方差矩阵:
P
k
[
p
p
0
2
1
p
]
3
p
先验协方差矩阵： ^
P
k
[
ˆ
p
ˆ
p
0
2
ˆ
1
p
]
ˆ
3
p
x
[
k
1
0
dt y
][ ]
k
1
v
[
1
1
2
2
dt
dt
]
a
k
^
P
k
T
AP A
k
R
[
ˆ
p
ˆ
p
0
2
ˆ
1
p
]
ˆ
3
p
[
1
0
dt p
][
1
p
0
2
1 1
p
][
3 0
p
dt
1
T
]
[
0
r
0
0
]
1
r
K
k
K
k
(
^
k
^
P H HP H
k
k
k
[
T
[
ˆ
0
p
ˆ
2
p
0
0
q
ˆ
2
p
ˆ
( 0
p
q
1
)
Q
ˆ
1
p
]([
ˆ
3
p
ˆ
p
ˆ
p
0
2
ˆ
p
ˆ
1
p
])
1
3
q
1
ˆ
0)( 3
p
1)
q
1
k
]
3
k
ˆ
p
0
2
ˆ
1
p
]([
ˆ
3
p
ˆ
1
p
]
ˆ
3
p
[
[
ˆ
p
ˆ
p
ˆ
p
ˆ
p
0
2
0
2
ˆ
1
p
]
ˆ
3
p
[
0
q
0
1
0
])
1
q
1
[
ˆ
3
p
1
q
ˆ
2
p
ˆ
0
p
ˆ
1
p
q
]
0
ˆ
ˆ
1 2
p p
x
x
k
(
K z
k
k
x
k
)
P
k
[
0
p
2
p
1
0
k
[
2
k
(
1
p
]
3
p
1
k
] [
1
3
k
I K H P
k
)
k
^
ˆ
p
ˆ
p
0
2
ˆ
1
p
]
ˆ
3
p
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
