logo资料库

有源模拟带通滤波器课程设计.doc

发布时间：2022-06-14 发布人：admin 分类：说明书 资料大小：0.83M 资料格式：doc 举报 版权申诉
第1页 / 共14页
第2页 / 共14页
第3页 / 共14页
第4页 / 共14页
第5页 / 共14页
第6页 / 共14页
第7页 / 共14页
第8页 / 共14页
资料共14页，剩余部分请下载后查看
    幅频特性曲线：
    四 遇到的问题
    在这次实践中我们遇到了一些问题，在最后阶段的调试时，我们才发现电容用错了，最后我们不得不重新焊
    五 项目总结
    一 项目目的 电子电路仿真项目是通信工程专业教学体系中一个实践性很强的环节。它将模拟电子线 路（低频部分和高频部分）、数字逻辑电路等课程的理论与实践有机结合起来，加强学生实 验基本技能的训练，培养学生实际动手能力、理论联系实践的能力。通过本课程设计让学生 掌握电子电路系统的设计、制作、调试、仿真的方法。 二 主要器件介绍 1 滤波器 滤波器是一种对信号有处理作用的器件或电路。其主要作用是让有用信号尽可能无衰 减的通过，对无用信号尽可能大的衰减。 滤波器一般有两个端口，一个输入信号、一个输出信号，利用这个特性可以将通过滤波 器的一个方波群或复合噪波，而得到一个特定频率的正弦波。 滤波器，顾名思义，是对波进行过滤的器件。滤波，本质上是从被噪声畸变和污染了的 信号中提取原始信号所携带的信息的过程。 2.滤波器的分类 2.1按所处理的信号 按所处理的信号分为模拟滤波器和数字滤波器两种。 2.2 按所通过信号的频段 按所通过信号的频段分为低通、高通、带通和带阻滤波器四种。 低通滤波器：它允许信号中的低频或直流分量通过，抑制高频分量或干扰和噪声。 高 通 滤 波 器 ： 它 允 许 信 号 中 的 高 频 分 量 通 过 ， 抑 制 低 频 或 直 流 分 量。 、 带通滤波器：它允许一定频段的信号通过，抑制低于或高于该频段的信号、干扰和噪 声。 、 带阻滤波器：它抑制一定频段内的信号，允许该频段以外的信号通过。 2.3 按所采用的元器件 按所采用的元器件分为无源和有源滤波器两种。 2.3.1、无源滤波器：仅由无源元件(R、L 和 C)组成的滤波器，它是利用电容和电感 元件的电抗随频率的变化而变化的原理构成的。这类滤波器的优点是：电路比较简单，不需 要直流电源供电，可靠性高；缺点是：通带内的信号有能量损耗，负载效应比较明显，使用 电感元件时容易引起电磁感应，当电感 L 较大时滤波器的体积和重量都比较大，在低频域 不适用。 2.3.2、有源滤波器：由无源元件(一般用 R 和 C)和有源器件（如集成运算放大器）组 成。这类滤波器的优点是：通带内的信号不仅没有能量损耗，而且还可以放大，负载效应不 明显，多级相联时相互影响很小，利用级联的简单方法很容易构成高阶滤波器，并且滤波器 1
    的体积小、重量轻、不需要磁屏蔽(由于不使用电感元件）；缺点是：通带范围受有源器件(如 集成运算放大器）的带宽限制，需要直流电源供电，可靠性不如无源滤波器高，在高压、高 频、大功率的场合不适用。 1)基本原理： 有源电力滤波器，是采用现代电力电子技术和基于高速 DSP 器件的数字信号处理技术 制成的新型电力谐波治理专用设备。它由指令电流运算电路和补偿电流发生电路两个主要部 分组成。指令电流运算电路实时监视线路中的电流，并将模拟电流信号转换为数字信号，送 入高速数字信号处理器（DSP）对信号进行处理，将谐波与基波分离，并以脉宽调制（PWM） 信号形式向补偿电流发生电路送出驱动脉冲，驱动 IGBT 或 IPM 功率模块，生成与电网谐 波电流幅值相等、极性相反的补偿电流注入电网，对谐波电流进行补偿或抵消，主动消除电 力谐波。 2)应用 通信行业为了满足大规模数据中心机房的运行需要，通信配电系统中的 UPS 使用容量 在大幅上升。据调查，通信低压配电系统主要的谐波源设备为 UPS、开关电源、变频空调 等。其产生的谐波含量都较高，且这些谐波源设备的位移功率因数极高。通过使用有源滤波 器可以提高通信系统及配电系统的稳定性，延长通信设备及电力设备的使用寿命，并且使配 电系统更符合谐波环境的设计规范。 2.4 无源滤波器和有源滤波器，存在以下的区别： 2.4.1工作原理 无源滤波器由 LC 等被动元件组成，将其设计为某频率下极低阻抗，对相应频率谐波电 流进行分流，其行为模式为提供被动式谐波电流旁路通道；而有源滤波器由电力电子元件和 DSP 等构成的电能变换设备，检测负载谐波电流并主动提供对应的补偿电流，补偿后的源 电流几乎为纯正弦波，其行为模式为主动式电流源输出。 2.4.2谐波处理能力 无源滤波器只能滤除固定次数的谐波；但完全可以解决系统中的谐波问题，解决企 业用电过程中的实际问题，且可以达到国家电力部门的标准；有源滤波器可动态滤除各次谐 波。 2.4.3系统阻抗变化的影响 无源滤波器受系统阻抗影响严重，存在谐波放大和共振的危险；而有源滤波不受影响。 2.4.4频率变化的影响 无源滤波器谐振点偏移，效果降低；有源滤波器不受影响。 2.4.5负载增加的影响 无源滤波器可能因为超载而损坏；有源滤波器无损坏之危险，谐波量大于补偿能力时， 仅发生补偿效果不足而已。 2.4.6负载变化对谐波补偿效果的影响 无源滤波器补偿效果随着负载的变化而变化；有源滤波器不受负载变化影响。 2
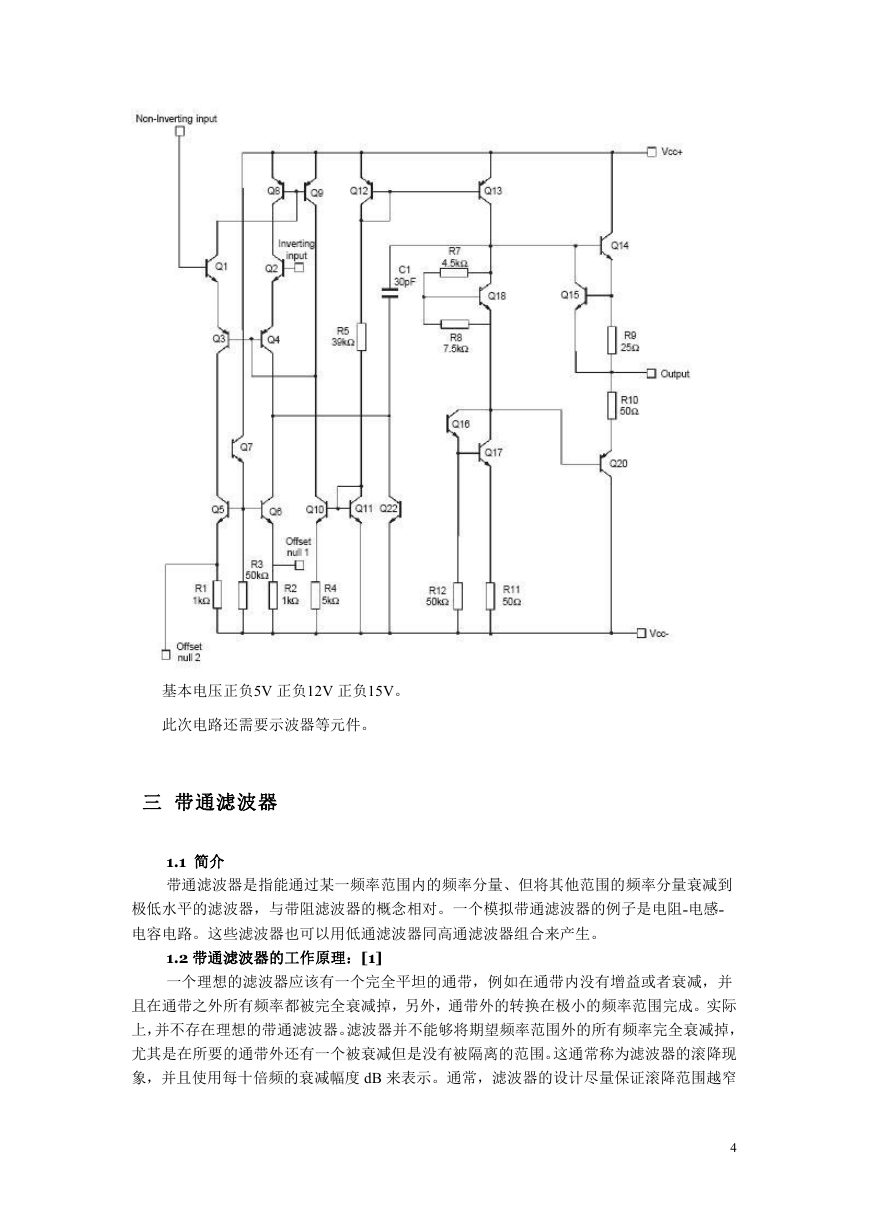
    2.4.7设备造价 无源滤波器较低；有源滤波器太高。 2.4.8应用场合对比分析 1.有源滤波容量单套不超过100KVA，无源滤波则无此限制； 2.有源滤波在提供滤波时，不能或很少提供无功功率补偿，因为要占容量；而无源滤波则同 时提供无功功率补偿。 3.有源滤波目前最高适用电网电压不超过450V，而低压无源滤波最高适用电网电压可达 3000V。 4.无源滤波由于其价格优势、且不受硬件限制，广泛用于电力、油田、钢铁、冶金、煤矿、 石化、造船、汽车、电铁、新能源等行业；有源滤波器因无法解决的硬件问题，在大容量场 合无法使用，适用于电信、医院等用电功率较小且谐波频率较高的单位，优于无源滤波。 3 运放741 uA741M，uA741I，uA741C（单运放）是高增益运算放大器，用于军事，工业和商业应用. 这类单片硅集成电路器件提供输出短路保护和闭锁自由运作。 这些类型还具有广泛的共同模式，差模信号范围和低失调电压调零能力与使用适当的电位。 uA741M，uA741I，uA741C 芯片引脚和工作说明： 1 和 5 为偏置(调零端)，2 为正向输入端，3 为反向输入端，4 接地，6 为输出，7 接电源 8 空 脚 3
    基本电压正负5V 正负12V 正负15V。 此次电路还需要示波器等元件。 三 带通滤波器 1.1 简介 带通滤波器是指能通过某一频率范围内的频率分量、但将其他范围的频率分量衰减到 极低水平的滤波器，与带阻滤波器的概念相对。一个模拟带通滤波器的例子是电阻-电感- 电容电路。这些滤波器也可以用低通滤波器同高通滤波器组合来产生。 1.2 带通滤波器的工作原理：[1] 一个理想的滤波器应该有一个完全平坦的通带，例如在通带内没有增益或者衰减，并 且在通带之外所有频率都被完全衰减掉，另外，通带外的转换在极小的频率范围完成。实际 上，并不存在理想的带通滤波器。滤波器并不能够将期望频率范围外的所有频率完全衰减掉， 尤其是在所要的通带外还有一个被衰减但是没有被隔离的范围。这通常称为滤波器的滚降现 象，并且使用每十倍频的衰减幅度 dB 来表示。通常，滤波器的设计尽量保证滚降范围越窄 4
    越好，这样滤波器的性能就与设计更加接近。然而，随着滚降范围越来越小，通带就变得不 再平坦—开始出现“波纹”。这种现象在通带的边缘处尤其明显，这种效应称为吉布斯现象。 除了电子学和信号处理领域之外，带通滤波器应用的一个例子是在大气科学领域，很 常见的例子是使用带通滤波器过滤最近 3 到 10 天时间范围内的天气数据，这样在数据域中 就只保留了作为扰动的气旋。 在频带较低的剪切频率 f1 和较高的剪切频率 f2 之间是共振 频率，这里滤波器的增益最大，滤波器的带宽就是 f2 和 f1 之间的差值。许多音响装置的频 谱分析器均使用此电路作为带通滤波器，以选出各个不同频段的信号，在显示上利用发光二 极管点亮的多少来指示出信号幅度的大小。这种有源带通滤波器的中心频率 ，在中心频率 0f 处的电压增益 A  0 B 3 2B 1 ，品质因数 ，3dB 带宽 B    1 cR  3 也可根据设计确定的 Q、 R 1 fo、Ao 值，去求出带通滤波器的各元件参数值。  Q 2 CAf 0 0 ， R 2  Q   2 AQ 0  2 Cf  0 2 ， R 3  2 Q 2 Cf  0 f 0  1 KHz 。上式中，当 f 。此电路亦可用于一般的选频放 大。 有源带通滤波器电路，此电路亦可使用单电源，只需将运放正输入端偏置在 1/2V+并 将电阻 R2 下端接到运放正输入端既可。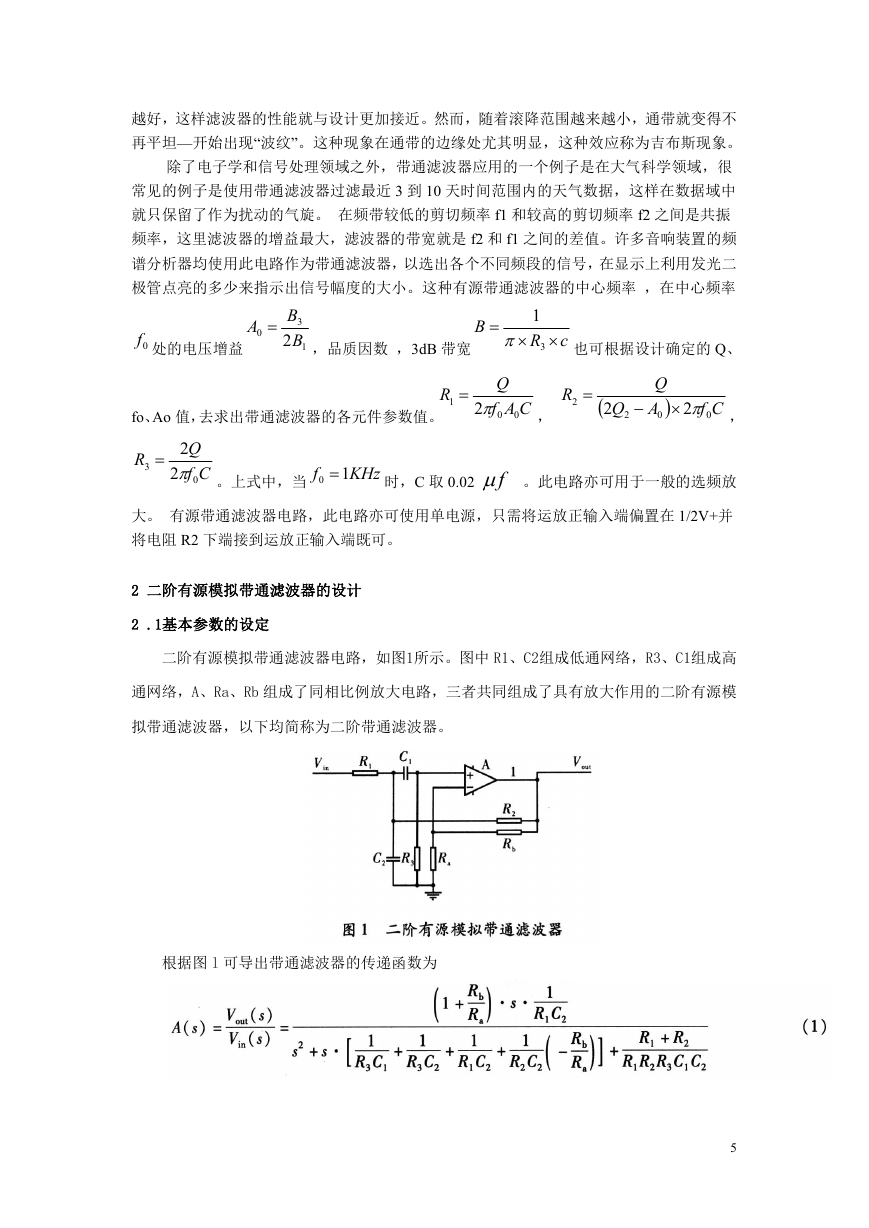 时，C 取 0.02 2 二阶有源模拟带通滤波器的设计 2 .1基本参数的设定 二阶有源模拟带通滤波器电路，如图1所示。图中 R1、C2组成低通网络，R3、C1组成高 通网络，A、Ra、Rb 组成了同相比例放大电路，三者共同组成了具有放大作用的二阶有源模 拟带通滤波器，以下均简称为二阶带通滤波器。 根据图 l 可导出带通滤波器的传递函数为 5
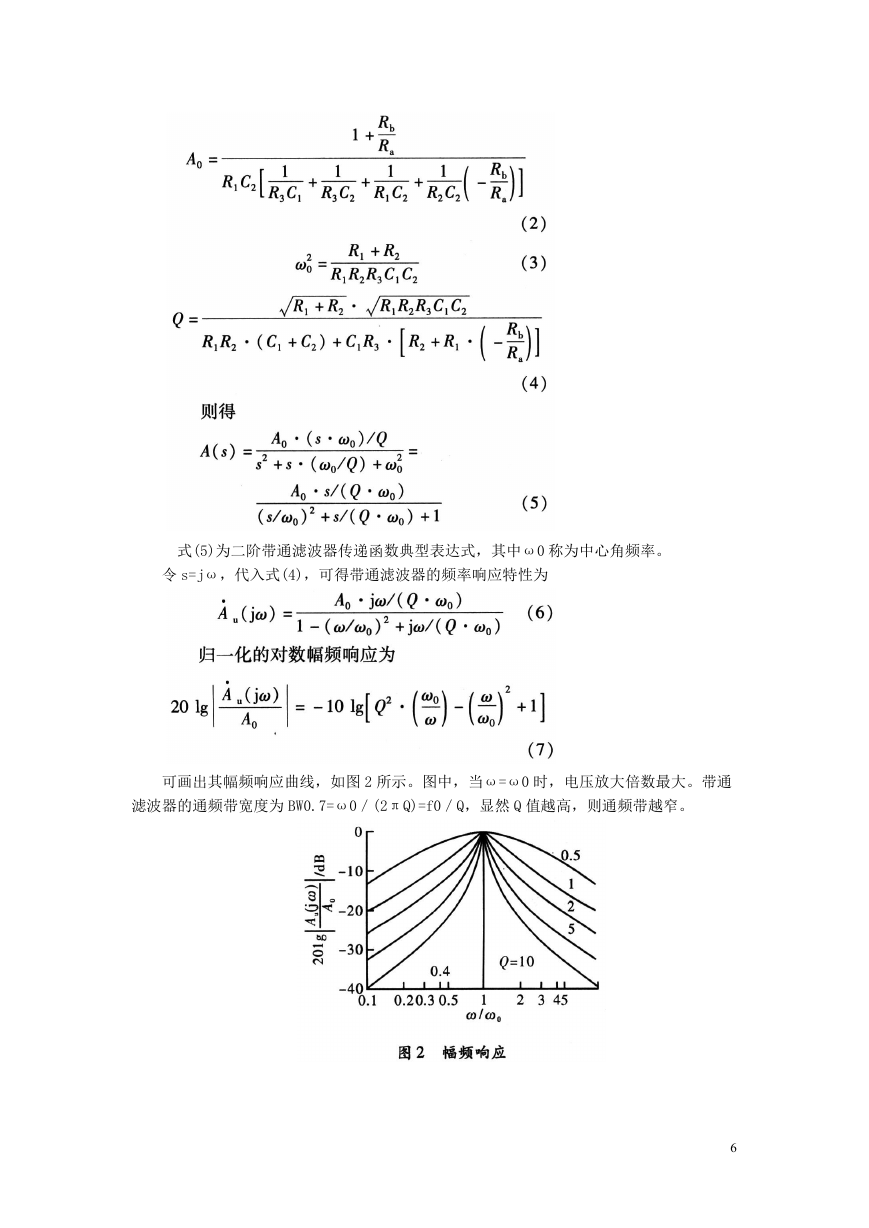
    式(5)为二阶带通滤波器传递函数典型表达式，其中ω0 称为中心角频率。 令 s=jω，代入式(4)，可得带通滤波器的频率响应特性为 可画出其幅频响应曲线，如图 2 所示。图中，当ω=ω0 时，电压放大倍数最大。带通 滤波器的通频带宽度为 BW0.7=ω0／(2πQ)=f0／Q，显然 Q 值越高，则通频带越窄。 6
    通频带越窄，说明其对频率的选择性就越好，抑制能力也就越强。理想的幅频特性应该 是宽度为 BW0.7 的矩形曲线，如图 3(a)所示。在通频带内 A(f)是平坦的，而通带外的各种 干扰信号却具有无限抑制能力。各种带通滤波器总是力求趋近理想矩形特性。 然而实际设计出来的带通滤波器的幅频特性曲线，如图 3(b)所示。 在工程上，定义增益自 A(f0)下降 3 dB(即 0．707 倍)时的上、下限频率之差值为通频带， 用 BW0.7 表示。要求其值大于有用信号的频谱宽度，保证信号的不失真传输。 综上分析可知：当有源带通滤波器的同相放大倍数 变化时，既影响通带增 益 A0，又影响 Q 值(进而影响通频带 BW0.7)，而中心角频率ω0 与通带增益 A0 无关。 3.1.2 课题要求 带通滤波的设计 设计要求：要求设计一个有源二阶带通滤波器，通带中心频率为 500Hz，通带中心频率 处的电压放大倍数为 10；带宽为 50Hz。根据要求，选用相应的元件实现带通滤波器电路， 并对进行仿真和制作，并能利用相关仪器测量其技术指标，通过示波器观察结果。 通带中心频率 通带中心频率处的电压放大倍数： 带宽： 设计方案 为了能了解二阶带通滤波器在实际电路中应用的效果，设计了如图 1 的电路进行实验验 证。图中 U1A 部分为放大电路，UlB 部分为二阶带通滤波器电路。 根据式(2)~式(4)，设计出了中心频率在 500Hz 附近，品质因素 Q 为 10，频带宽度约为 50Hz 的二阶带通滤波器 。 有题可知 Q=10 ;f=500HZ;BW=50HZ;Au=10 7
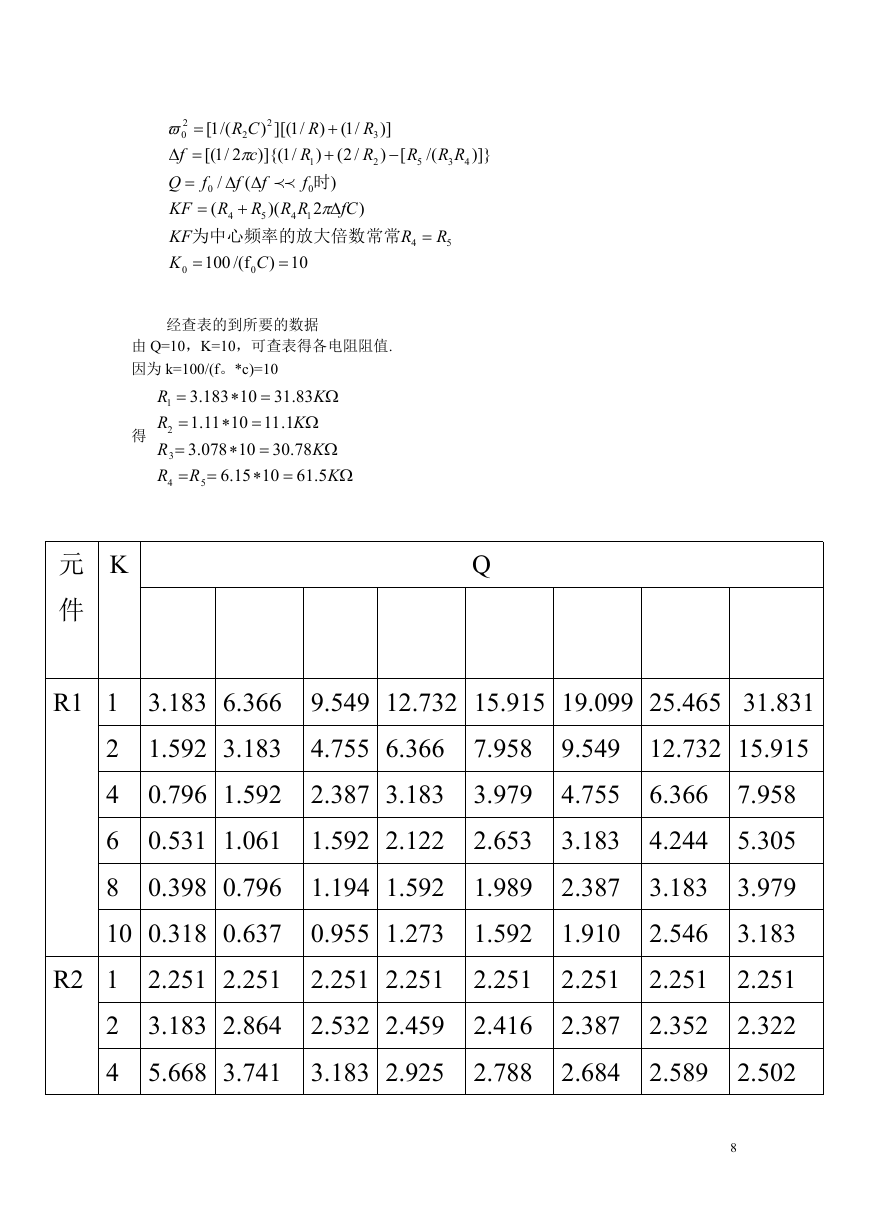
    /(1[ CR 2 2/1[( c  ( / f  R  4 /1][( ) ) /1( R  ) )]{( /1 /2( R  1 ) f f  时 0 )( 2 RRR   5 1 2   0 f  fQ  ) fC KF  KF 为中心频率的放大倍数 K  100 10 f/( 0 ( C  ) 4 0 0 2 R 3 R 2 )] )  [ RRR 5 4 /( 3 常常 R 4  R 5 经查表的到所要的数据 由 Q=10，K=10，可查表得各电阻阻值. 因为 k=100/(f。*c)=10 183 83.31 10 .3 K   11.1 1.11 10 K    078 .3 10 78.30 K    15.6 5.61 10 R K        R 1 R 2 R R 4   得 3 5 )]} Q K 元 件 3.183 6.366 R1 1 1.592 3.183 2 0.796 1.592 4 0.531 1.061 6 0.398 0.796 8 10 0.318 0.637 2.251 2.251 3.183 2.864 5.668 3.741 R2 1 2 4 9.549 12.732 15.915 19.099 25.465 31.831 4.755 6.366 12.732 15.915 7.958 6.366 2.387 3.183 1.592 2.122 4.244 5.305 3.979 3.183 1.194 1.592 3.183 2.546 0.955 1.273 2.251 2.251 2.251 2.251 2.322 2.352 2.532 2.459 2.502 2.589 3.183 2.925 7.958 3.979 2.653 1.989 1.592 2.251 2.416 2.788 9.549 4.755 3.183 2.387 1.910 2.251 2.387 2.684 8
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料