Tutorial.docx-资料库

weixin_43145941-16623116-16359647376563163358.docx.pdf-第1页.png

第1页 / 共25页

weixin_43145941-16623116-16359647376563163358.docx.pdf-第2页.png

第2页 / 共25页

weixin_43145941-16623116-16359647376563163358.docx.pdf-第3页.png

第3页 / 共25页

weixin_43145941-16623116-16359647376563163358.docx.pdf-第4页.png

第4页 / 共25页

weixin_43145941-16623116-16359647376563163358.docx.pdf-第5页.png

第5页 / 共25页

weixin_43145941-16623116-16359647376563163358.docx.pdf-第6页.png

第6页 / 共25页

weixin_43145941-16623116-16359647376563163358.docx.pdf-第7页.png

第7页 / 共25页

weixin_43145941-16623116-16359647376563163358.docx.pdf-第8页.png

第8页 / 共25页

QAV

摘要针对四旋翼飞行器(QAV)轨迹跟踪控制性能易受模型参数不确定性和未知外部干扰影响的问题，提出一种简单高效的串级比例微分(PD)控制策略。其中内环为姿态环，外环为位置环。文章首先给出了 QAV 常用坐标系，并给出了其中地面坐标系与机体坐标系之间的变换矩阵，随后针对四旋翼的运动学和动力学模型建模，推导出了描述 QAV 在三维空间中运动状态的牛顿-欧拉方程。针对牛顿-欧拉方程的强耦合性，设计了一种串级控制器，并详细推导出了 QAV 四个旋翼的控制量，即所需的旋转角速度表达式。利用 Simulink 对 QAV 模型进行搭建，并将控制算法引入。实验仿真了 70s 内 QAV 从地面连续跟踪 3 个变化点位并最终返回原点的轨迹图，实验结果表面控制策略具有简单高效的特点。文末给出了一些未来 QAV 控制策略研究的展望。关键词：QAV，串级控制，PD 控制，牛顿-欧拉方程，Simulink I

目录摘要.............................................................................................................................................I 1. 介绍................................................................................................................................. - 1 - 2. 飞行器坐标系介绍......................................................................................................... - 1 - 2.1 几种飞行器基本坐标系......................................................................................- 1 - 2.2 机体坐标系与地面坐标系转换..........................................................................- 2 - 3. 四旋翼飞行器建模......................................................................................................... - 4 - 3.1 四旋翼飞行器运动学建模..................................................................................- 4 - 3.2 四旋翼飞行器动力学建模..................................................................................- 5 - 3.3 四旋翼飞行器牛顿-欧拉方程.............................................................................- 7 - 4. 控制器设计..................................................................................................................... - 8 - 4.1 串级控制概述......................................................................................................- 8 - 4.2 四旋翼飞行器串级控制框图..............................................................................- 8 - 4.3 四旋翼飞行器位置控制......................................................................................- 9 - 4.4 四旋翼飞行器姿态控制....................................................................................- 10 - 5. Simulink 模型搭建与 MATLAB 脚本书写.................................................................. - 11 - 5.1 四旋翼飞行器模型在 Simulink 下的搭建细节............................................... - 11 - 5.1.1 姿态角 Simulink 搭建.............................................................................- 12 - 5.1.2 位置 Simulink 搭建.................................................................................- 13 - PD 串级控制器的搭建细节..............................................................................- 15 - 5.2 5.3 仿真结果及其分析............................................................................................- 16 - 6. 结论............................................................................................................................... - 19 - 7. 未来展望....................................................................................................................... - 19 - 8. 参考文献....................................................................................................................... - 19 - 附录..................................................................................................................................... - 20 - II

1. 介绍四旋翼无人飞行器(Quadrotor Unmanned Aerial Vehicle, QAV)具有结构简单、成本低廉、操作灵巧等优点,可实现垂直起降、定点悬停等运动,近年来在军事和民用领域的应用激增，如航空摄影、物流运输、农林植保、巡航监视等[1][2]。其中，轨迹跟踪控制算法是 QAV 执行各种任务的前提之一[3][4]。然而，QAV 的非线性、强耦合、欠驱动等复杂的动力学特性给控制算法的设计带来了一定的挑战。另外，由外部干扰(阵风、地面效应)和模型参数不确定性(如未建模动态、载荷变化、质量分布变化)构成的集总干扰也会导致飞行控制系统性能降低，甚至破坏系统的稳定性，进而加剧了控制算法的设计难度。为了提高 QAV 飞行控制系统的鲁棒性和抗干扰能力，学者们大都偏爱采用先进的控制策略来设计轨迹跟踪控制器。例如，一篇文献[4]中提出了一种分级控制结构，其中外层采用模型预测控制器(MPC)控制位置坐标，内层采用∞控制方法稳定姿态角并且控制航向; 然而，由于耦合作用的存在，无法证明系统的全局稳定性和全局鲁棒性。针对以上研究工作的问题，本文作者基于串级比例微分控制为 QAV 设计了一种全局鲁棒轨迹跟踪控制算法，其采用姿态、位置双闭环串级控制器对 QAV 进行控制。本文的结构如下：第 2 部分介绍飞行器常用坐标系，第 3 部分详细阐述对 QAV 的建模过程，第 4 部分说明串级控制器的设计过程，第 5 部分为 Simulink 的仿真以及实验结果分析，第 6 部分为结论，第 7 部分为未来展望。 2. 飞行器坐标系介绍 2.1 几种飞行器基本坐标系根据飞行器的运动学特性，通常成立速度三角形关系： V K  (1) V V W  A 其中，为飞行器的对地速度（即航迹速度）向量，为对空速度（即飞行速度）向量，为当前时刻飞行器质心处的风速向量。假设忽略地球曲率和旋转，为建立飞行器的运动方程，首先定义以下几种常用的右手直角坐标系: - 1 -

点，（1）地面坐标系()和''''(')。对于，其原点为地面上某一固定轴、分别指向地平面的北向和东向，轴按右手定则铅垂向下。对于' ，其原点' 与重合，轴' 、' 分别指向地平面的北向和西向，轴' 按右手定则铅垂向上。（2）航迹坐标系()和''''(')：对于，其原点为飞行器质心，轴指向飞行器的地速方向，轴在通过轴的铅垂平面内垂直于轴，指向下；轴垂直于平面，指向右。对于' ，其原点' 和轴' 分别重合于和轴，而轴' 和' 的指向则分别与轴和相反，即分别在相应平面内指向上和左。（3）机体坐标系()。其原点为飞行器质心，轴在飞行器对称平面内指向机体纵轴方向，轴在对称面内垂直于轴，指向下；轴垂直于对称平面，指向右。（4）气流坐标系（又称速度系）()。其原点为飞行器质心，轴指向飞行器的空速方向，轴在飞行器对称平面内垂直于轴，指向下；轴垂直于平面，指向右。本文的算法建立在第(1)和第(3)种坐标系即地面坐标系和机体坐标系上，其中地面坐标系主要用来表示 QAV 所处的空间位置，而机体坐标系主要用来表示 QAV 的姿态。两者合并可同时表示出 QAV 在空间任意位置的任意姿态，即对 QAV 的完全描述。 2.2 机体坐标系与地面坐标系转换任意两个坐标系间的转换关系可由一组 Euler 角确定。假设任意的一个坐标系绕某一坐标轴转过 Euler 角 a,该过程可由一组基元坐标变换矩阵表示，其公式为：   ( ) T a  x     ( ) T a  y     ( ) T a  z     0 cos a sin a  0 a 1 0 1   0   0  cos   0   sin a  cos a   sin a     0  sin cos 0 0 sin cos sin  0 cos a a                a a a a 0 0 1 (2) 其中，基元坐标变换矩阵 T 的下标表示旋转时所绕的坐标轴。坐标系间的转换关系可由基元坐标变换矩阵的组合表示。 - 2 -

T bg  T x ( ) ) T    ( ) T ( 的夹角，飞行器右翼下倾时为正。根据坐标变换的原理，对于空间中的任意一个向量以及坐标系1和2，成立等式 =11=22，其中1和2分别为向量在基1和2下的坐标向量。假设由1到2的坐标变换矩阵为21=()()()，则有2=211。为讨论地面系和机体系之间的关系，首先定义偏航角、俯仰角和滚转角。其中，偏航角为飞行器纵轴正向在水平面的投影与轴之间的夹角，投影相对于轴向右旋转时为正；俯仰角为飞行器纵轴正向与水平面之间的夹角，纵轴正向指向水平面上方时为正；滚转角为飞机对称平面与通过飞行器纵轴的铅垂面之间基于上述定义，可实现和间的相互转换。以从转换到为例，首先绕轴转过偏航角，再按当时的轴转过俯仰角，最后按当时的轴转过滚转角，即与重合。由到的旋转矩阵为：上式即为世界坐标系到机体坐标系的旋转矩阵，这里值得注意的是，会根据定义欧拉角旋转顺序的不同而不同，例如以顺序,,旋转坐标轴某个角度和以顺序,,旋转坐标轴某个角度得到的旋转矩阵是不相同的。为了统一之后的运算，在之后提及均指顺序,,。 = = 1 0 0 = cos sin 0 1 cos 0 −sin sin cos 0 1 −sin cos 0 0 0 0 −sin cos cos sin 0 0 0 = cc css−sc scc+ss sc sss+cc scs −s cs cc 其中代表，代表，这里默认旋转顺序为,,，后面在提及时均指在该顺序至此我们推导出了地面坐标系到机体坐标系旋转矩阵以及机体坐标系到地面坐标系的旋转矩阵。同理我们可以推出从机体坐标系到世界坐标系的旋转矩阵：旋转所得到的旋转矩阵。 (3) (4) y z - 3 -

3. 四旋翼飞行器建模 3.1 四旋翼飞行器运动学建模讨论问题。对四旋翼飞行器的运动学建模实质上是应用牛顿第二定律将飞行器当做质点处理后对其受力分析。由于在这一部分 QAV 为质点，因此先在地面坐标系()下提供在机体坐标系()下垂直向上的升力，其四个旋翼中相对的一组旋翼旋转在进行运动学建模之前首先对 QAV 的动力源做一个介绍：QAV 通过四个旋翼旋转方向相同，剩余一组旋翼旋转方向与另一组相反，这样做的目的是抵消反转力矩，从而保证 QAV 在悬停状态下不会发生偏航角的变化。 QAV 质点在地面坐标下有：为 QAV 受到的合力，为方向上的加速度，为方向上的加速度，为方向上的加速度。 QAV 受到的力主要有两个，一个是自身的重力，另一个是四个旋翼提升的升力，将其代入(5)式： = (5) (6) (7) 1+2+3+4 − 00 = 00 其中1,2,3,4为 QAV 四个旋翼提供的升力，为 QAV 的质量，为重力加速度。由于1,2,3,4是由四个电机产生，故他们的作用方向都在机体坐标系的轴方向，而重力方向却在地面坐标系的轴方向，因此考虑将1,2,3,4转化到地面坐标系下讨论，于是将(6)式改写为： 1+2+3+4 − 00 = 00 其中用(4)式计算。将上式的加速度用位移的二阶导数表示并将代入可得： - 4 -

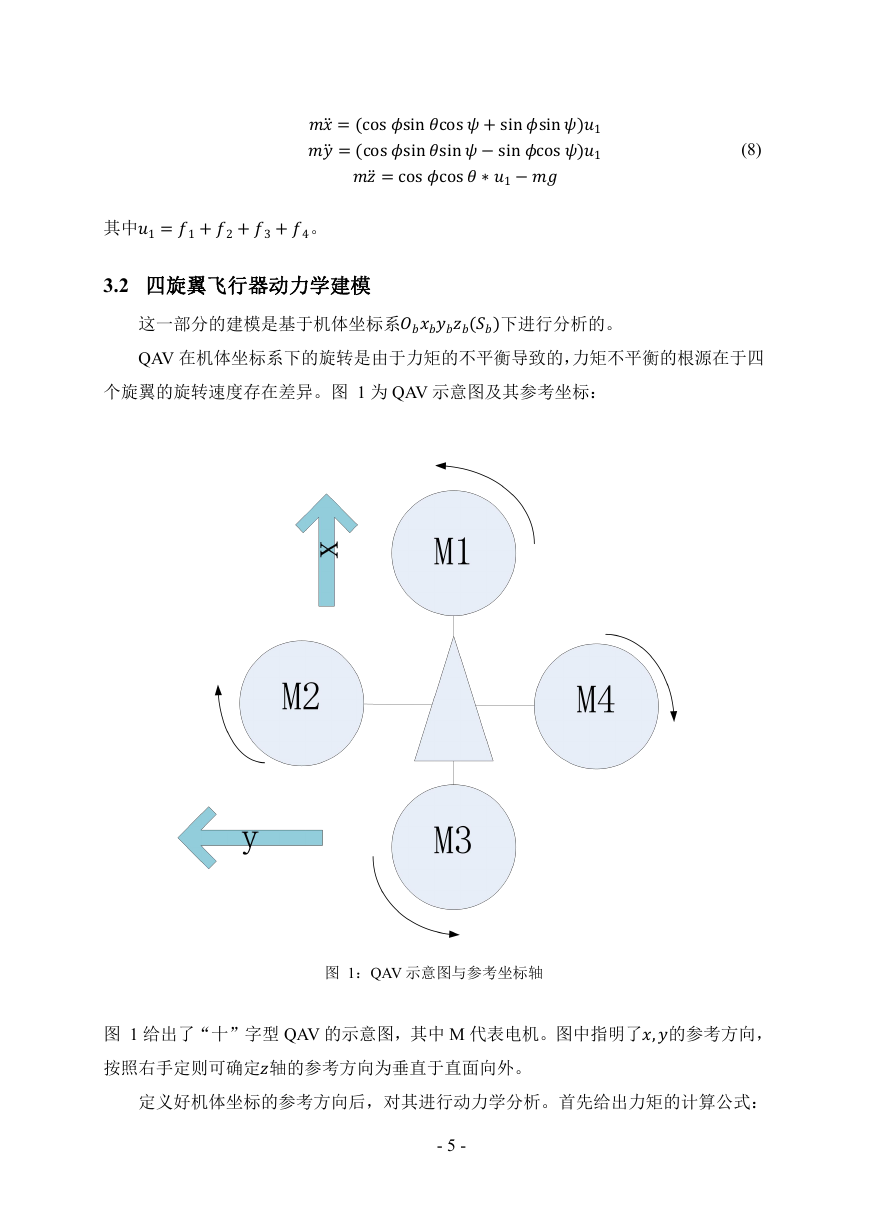
=(cos sin cos +sin sin )1 =(cos sin sin −sin cos )1 =cos cos ∗1− 其中1=1+2+3+4。这一部分的建模是基于机体坐标系()下进行分析的。 3.2 四旋翼飞行器动力学建模 (8) QAV 在机体坐标系下的旋转是由于力矩的不平衡导致的，力矩不平衡的根源在于四个旋翼的旋转速度存在差异。图 1 为 QAV 示意图及其参考坐标：图 1：QAV 示意图与参考坐标轴图 1 给出了“十”字型 QAV 的示意图，其中 M 代表电机。图中指明了,的参考方向，按照右手定则可确定轴的参考方向为垂直于直面向外。定义好机体坐标的参考方向后，对其进行动力学分析。首先给出力矩的计算公式： - 5 -

资料库

Tutorial.docx

相关推荐

课程资源

热门标签

最新资料