2006年河南安阳中考数学真题及答案.doc

发布时间：2022-08-25 发布人：admin 分类：说明书资料大小：1.02M 资料格式：doc 举报版权申诉

第1页 / 共6页

第2页 / 共6页

第3页 / 共6页

第4页 / 共6页

第5页 / 共6页

第6页 / 共6页

文本预览

2006 年河南安阳中考数学真题及答案一、选择题（每小题 3 分，共 18 分）下列各小题均有四个答案，其中只有一个是正确的，将正确答案的代号字母填入题后括号内．  的倒数是（ 1． 1 2 Ａ． 2 ） 1 2 Ｂ．Ｄ． 2  Ｃ． 1 2 ）Ｃ． 2 个Ｂ．3 个 2．下列图形中，是轴对称图形的有（Ａ． 4 个 3．两条直线相交所成的四个角中，下列说法正确的是（Ａ．一定有一个锐角Ｃ．一定有一个直角 4．当三角形的面积 S 为常数时，底边 a 与底边上的高 h 的函数关系的图象大致是（Ｂ．一定有一个钝角Ｄ．一定有一个不是钝角Ｄ．1个））Ｂ． 4 :1 5．如图，把半径为1的四分之三圆形纸片沿半径OA 剪开，依次用得到的半圆形纸片和四分之一圆形纸片做成两个圆锥的侧面，则这两个圆锥的底面积之比为（Ａ．5:1 6．某公园的两个花圃，面积相等，形状分别为正三角形和正六边形．已知正三角形花圃的周长为50 米，则正六）边形花圃的周长（Ａ．Ｂ．等于50 米Ａ．大于50 米二、填空题（每小题 3 分，共 21 分）Ｃ．小于50 米（第 5 题）Ｄ．无法确定Ｄ． 2 :1 Ｃ．3:1 Ｂ．Ｃ．Ｄ．） 7．计算： y  8．函数 3    _______________． 0 2 1  1 中，自变量 x 的取值范围是_______________．  5 x （第 10 题） 9．蜜蜂建造的蜂房既坚固又省料．蜂房的巢壁厚约 0.000 073 米，用科学记数法表示为_______________米． 10．如图所示，把腰长为1的等腰直角三角形折叠两次后，得到的一个小三角形的周长是_______________． 11．方程组 y x 3    2 5   x 2 y    的解是_______________． 12．如图， O 从直线 AB 上的点 A （圆心O 与点 A 重合）出发，沿直线 AB 以1厘米／秒的速度向右运动（圆 AB  厘米， O ， B 的半径分别为1厘米和 2 厘米．当两圆相交时， O 心O 始终在直线 AB 上）．已知线段的运动时间t （秒）的取值范围是____________ __________________． 13．如图（1），用形状相同、大小不等的三块直角三角形木板，恰好能拼成如图（2）所示的四边形 ABCD ．若 AE  ，三、解答题（本大题共 9 个小题，满分 61 分），那么这个四边形的面积是_______________．图（2）图（1） 3 BE CE 4 6  （第 12 题）（第 13 题） 14．（5 分）先化简，再求值：     15．（ 5 分）如图，在 ABCD 中， E 为 CD 的中点，连结 AE 并延长交 BC 的延长线于点 F ．求证： S ，其中 1005 11   x  x   x  ．． 9 3    2 x 2 x  x  x △ ABF S  ABCD 16．（6 分）在一次演讲比赛中，七位评委为其中一位选手打出的分数如下：（1）这组数据的中位数是___________，众数是___________，平均分 x  ___________，去掉一个最高分和一个

最低分后的平均分 1x  ___________；（2）由（1）所得的数据 x ， 1x 和众数中，你认为哪个数据能反映演讲者的水平？为什么？ 17．（6 分）同一种商品在甲、乙两个商场的标价都是每件10 元，在销售时都有一定的优惠．甲的优惠条件是：购买不超过10 件按原价销售，超过10 件，超出部分按7 折优惠；乙的优惠条件是：无论买多少件都按9 折优惠．（1）分别写出顾客在甲、乙两个商场购买这种商品应付金额 y甲（元）， y乙（元）与购买件数 x （件）之间的函数关系式；（2）某顾客想购买这种商品 20 件，他到哪个商场购买更实惠？ 18．（6 分）关于 x 的一元二次方程 2 x mx m  19．（7 分）如图，山顶建有一座铁塔，塔高    的两个实数根为 1x ， 2x ，且 2 x 1 BC  米，测量人员在一个小山坡的 P 处测得塔的底部 B 点的仰  ，求实数 m 的值． 1 0 80 2 x 2 5 角为 45 ，塔顶C 点的仰角为 60 ．已测得小山坡的坡角为30 ，坡长 MP  米．求山的高度 AB （精确到1 40 米）．（参考数据： 2 1.414  ， 3 1.732  ） 20．（7 分）如图， ∠ AOB  45  ，过OA 上到点O 的距离分别为1，2 ，3 ，4 ，5 的点作OA 的垂线与 OB 相交，再按一定规律标出一组如图所示的黑色梯形．设前 n 个黑色梯形的面积和为 nS ．（1）请完成下面的表格： 1 2 3 （2）已知 nS 与 n 之间满足一个二次函数关系，试求出这个二次函数的解析式． 21．（9 分）如图， AB 为 O 的直径， AC ， BD 分别和 O 相切于点 A ， B ，点 E 为圆上不与 A ， B 重合的点，过点 E 作 O 的切线分别交 AC ， BD 于点C ， D ，连结OC ，OD 分别交 AE ， BE 于点 M ， N ．（1）若（2）当点 E 在 O 上运动时，试判定四边形OMEN 的形状，并给出证明． BD  ，求 O 的半径及弦 AE 的长； AC  ， 4 9 22．（10 分）二次函数 y 的图象如图所示，过 y 轴上一点  0 2M ，的直线与抛物线交于 A ， B 两点，过点 21 x 8 A ， B 分别作 y 轴的垂线，垂足分别为C ， D ．（1）当点 A 的横坐标为 2 时，求点 B 的坐标；（2）在（1）的情况下，分别过点 A ，B 作 AE 为直角．若存在，求点 P 的坐标；若不存在，请说明理由；（3）当点 A 在抛物线上运动时（点 A 与点O 不重合），求 AC BD 的值． x⊥ 轴于 E ，BF x⊥ 轴于 F ，在 EF 上是否存在点 P ，使 APB∠

数学试题参考答案及评分标准一、选择题（每小题 3 分，共 18 分）题号答案 1 Ａ 2 Ｃ 3 Ｄ 4 Ｂ 5 Ｂ 6 Ｃ二、填空题（每小题 3 分，共 21 分）题号 7 8 9 10 11 12 13 答案三、解答题（本大题共 9 个小题，满分 61 分） 3 t  或 5  ．·························································4 分．··································································· 5 分 x x x  4 1 ∠ x  3 2      时，原式 2006 14．解：原式当 1005 15．证明：四边形 ABCD 为平行四边形， AD BC ECF  ． E 是 DC 的中点， DE CE  ． △ S AED  DAE FEC △ ． ≌△   S F ∠ ， D ∠ ∠  ．·············································································· 3 分  ∥ ． △ AED FEC S  ABCD ····················································································5 分 16．（1）9.4 分，9.4 分，9.4 分，9.5 分．····················································4 分（2）答案不惟一，言之有理即可，如 1x ．理由： 1x 既反映了多数评委所打分数的平均值，又避免了个别评委打分过高或过低对选手成绩的影响． 6 分 17．解：（1）当购买件数 x 不超过10 件时， y 甲 10 x ；当购买件数 x 超过10 件时， y 甲 7 x  30 ．·················································· 2 分 9 y x乙．······························································································ 3 分（2）当 20 x  时， y 甲 170 ， y 乙 180 ．  甲 y y 乙． 若顾客想购买 20 件这种商品，到甲商场购买更实惠．·································· 6 分 1  ．········································· 1 分 x 18．解：由题意，得 1   ， 1 2 x x m x 2 m   2 x 1  2 x 2   x 1  x 2 2  2 x x 1 2  5 ，    m  2 2   m  1   ． 5 解得 1 3m  ， 2 m   ．··········································································· 4 分 1   1    m m m 2 4     3m  或 1 ．······················································································· 6 分 19．解：如图，过点 P 作 PE AM⊥ 于 E ， PF AB⊥ 于 F ． ≥ ， 2 0  2 在 Rt PME△ 中， ∠ PME   30 ， PM  ， 40 PE  ． 20

四边形 AEPF 是矩形，设 BF x 米．   FA PE  ．················································ 2 分 20 FPB  ∠   45  FP BF x  ．， ∠ FPC   60 ， tan 60  3 x ． CF PF 80   CB  x    80 ， 3 x ．解得 x  AB   40  40  3 1  ．···············································································6 分    20 60 40 3 129 （米）． 3 1    答：山高 AB 约为129 米．········································································· 7 分 20．解：（1） 1 2 3 ············································································································· 3 分（2）设二次函数的解析式为 nS  2 an  bn c  ．则， 3     a b c  2  5 4 2 a b c     21 9   2    a 3 b c  ，，解得 a    b  c  1 ， 1 2 0 ． ······························································· 6 分， 所求二次函数的解析式为 nS  2 n  ．···················································7 分 1 2 n 4  ．  ， DE BD 21．解：（1） AC ， BD ，CD 分别切 O 于 A ， B ， E ， CE AC   13 CD  ． AB 为 O 的直径，过点C 作CF BD⊥ 于 F ，则四边形 ABFC 是矩形． ABD BAC 90  ∠ ∠ ． 9    AC  ， 4 BD  ， 9 2 2  5 12 13 CF   ． 5 FD  ， AB  ， O 的半径为 6 ．································································ 3 分 12 连结OE ． CA CE OC 垂直平分弦 AE ．，OA OE ，  OC  2 6  2 4  2 13 ，  AM  AO AC  OC  12 13 13 ．

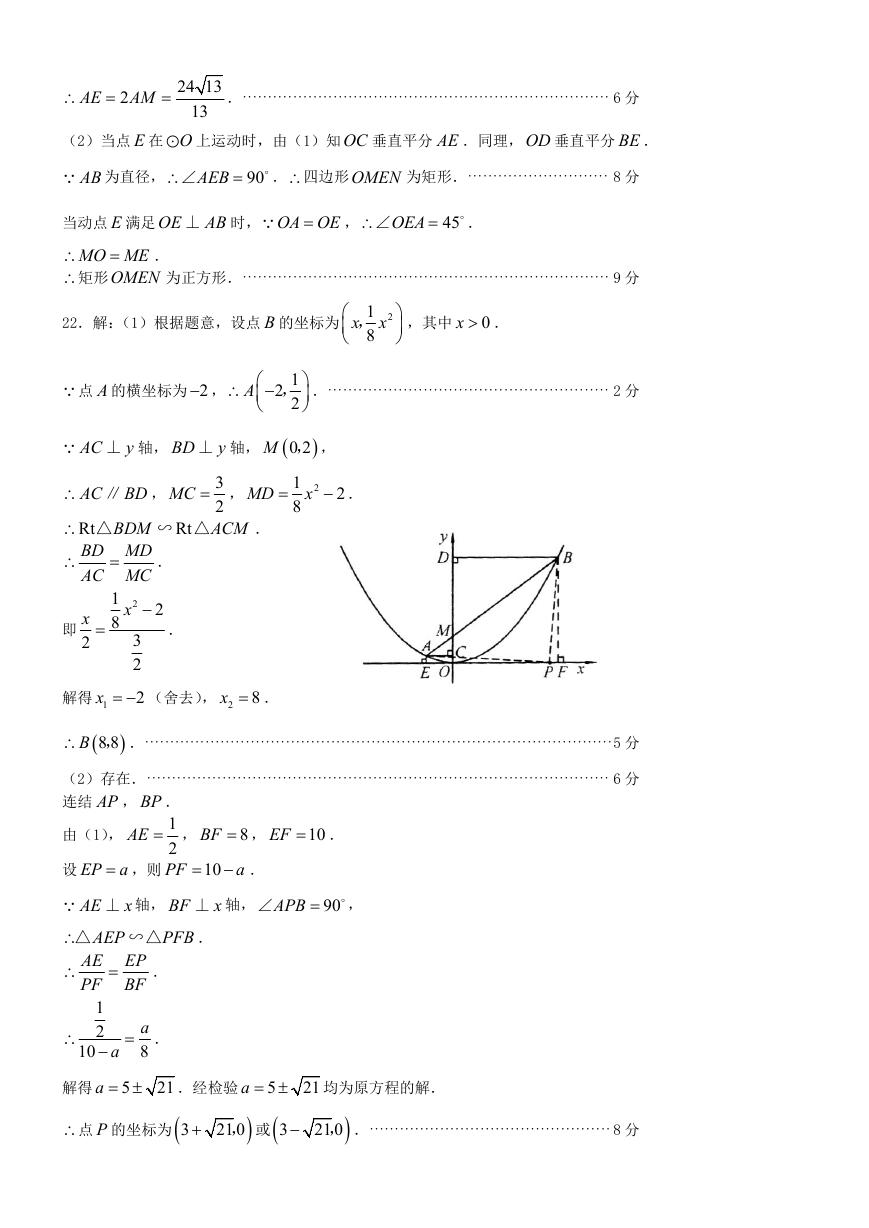
  AE 2 AM  24 13 13 ．········································································· 6 分（2）当点 E 在 O 上运动时，由（1）知OC 垂直平分 AE ．同理，OD 垂直平分 BE ． AB 为直径，．四边形OMEN 为矩形．···························· 8 分 AEB 90  ∠   AB⊥ 时， OA OE 当动点 E 满足OE  矩形OMEN 为正方形．········································································· 9 分 MO ME OEA 45   ∠ ．，．   22．解：（1）根据题意，设点 B 的坐标为    21 ，，其中 0 x x 8 x  ．    点 A 的横坐标为 2 ， A    12 ，．························································ 2 分 2     ⊥ 轴， BD y⊥ 轴，  0 2M ，， AC y MC  ， Rt 3 2 ACM ∽ △ MD ． 21 x 8  ． 2  ∥ ，  △ AC BD Rt BDM BD MD  AC MC  21 x 8  x 2  即． 2 ． 3 2 2 解得 1 x   （舍去）， 2 x  ． 8  8 8B ，．·····························································································5 分（2）存在．···························································································· 6 分连结 AP ， BP ． 1 2 PF BF  ， 10 设 EP a ，则 EF  ． AE  ，由（1），  ． 8 a 10  x⊥ 轴， ∠ APB   90 ，．  ∽△ EP BF x  ⊥ 轴， BF AE AEP PFB △ AE  PF 1 2   a 8 10 ．．  a a   解得 5 21 点 P 的坐标为 ．经检验 5 a    ，或  21 0 3 3 21 均为原方程的解．  ，．················································ 8 分 21 0 

（3）根据题意，设 21 A m m ， 8       ，  B n   21 n ，，不妨设 8    0m  ， 0 n  ．由（1）知，．·····················································································10 分 2   2 BD MD AC MC 1 n 8 12  8 mn  16 m  或 2 则 n m   化简，得 0 m n ≠ ， 16 mn   ． 16   AC BD  2 2 ． n 12  8 1 2 8  ． m 0  n m   m n  

分享到：

赞收藏

资料库

2006年河南安阳中考数学真题及答案.doc

相关推荐

中考

热门标签

最新资料